Теория сети — параллельный резонанс

В предыдущей главе мы обсуждали важность последовательного резонанса. Теперь давайте обсудим параллельный резонанс в цепях RLC.

Схема параллельного резонанса

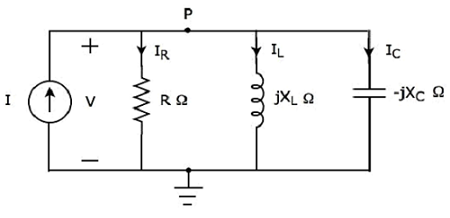
Если резонанс возникает в параллельной цепи RLC, то он называется параллельным резонансом . Рассмотрим следующую параллельную схему RLC , которая представлена ​​в векторной области.

Здесь пассивные элементы, такие как резистор, катушка индуктивности и конденсатор, соединены параллельно. Вся эта комбинация параллельна входному синусоидальному источнику тока.

Написать узловое уравнение в узле P.

$$- I + I_R + I_L + I_C = 0$$

$$\ Rightarrow - I + \ frac {V} {R} + \ frac {V} {j X_L} + \ frac {V} {- j X_C} = 0$$

$$\ Rightarrow I = \ frac {V} {R} - \ frac {jV} {X_L} + \ frac {jV} {X_C}$$

$\ Rightarrow I = V [\ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup]$ Уравнение 1

Приведенное выше уравнение имеет вид I = VY .

Следовательно, допуск Y параллельной цепи RLC будет

$$Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup$$

Параметры и электрические величины при резонансе

Теперь давайте по порядку выведем значения параметров и электрических величин при резонансе параллельной цепи RLC.

Резонансная частота

Мы знаем, что резонансная частота f _r — это частота, на которой возникает резонанс. В параллельной RLC цепи резонанс возникает, когда мнимый член допуска Y равен нулю. т.е. значение $\ frac {1} {X_C} - \ frac {1} {X_L}$ должно быть равно нулю

$$\ Rightarrow \ frac {1} {X_C} = \ frac {1} {X_L}$$

$$\ Rightarrow X_L = X_C$$

Вышеуказанное условие резонанса такое же, как и в последовательной цепи RLC. Таким образом, резонансная частота f _r будет одинаковой как в последовательной RLC-цепи, так и в параллельной RLC-схеме.

Следовательно, резонансная частота f _r параллельной RLC-схемы равна

$$f_r = \ frac {1} {2 \ pi \ sqrt {LC}}$$

Куда,

• L — индуктивность индуктора.
• С — емкость конденсатора.

Резонансная частота f _r параллельной цепи RLC зависит только от индуктивности L и емкости C. Но это не зависит от сопротивления R.

впуск

Мы получили допуск Y параллельной цепи RLC как

$$Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup$$

Замените $X_L = X_C$ в приведенном выше уравнении.

$$Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_C} \ rgroup$$

$$\ Rightarrow Y = \ frac {1} {R} + j (0)$$

$$\ Rightarrow Y = \ frac {1} {R}$$

При резонансе вход Y параллельной цепи RLC равен обратной величине сопротивления R. т.е. $\ mathbf {\ mathit {Y = \ frac {1} {R}}}$

Напряжение на каждом элементе

Замените $\ frac {1} {X_C} - \ frac {1} {X_L} = 0$ в уравнении 1

$$I = V [\ frac {1} {R} + j (0)]$$

$$\ Rightarrow I = \ frac {V} {R}$$

$$\ Rightarrow V = IR$$

Следовательно, напряжение на всех элементах параллельной цепи RLC при резонансе равно V = IR .

При резонансе допуск параллельной цепи RLC достигает минимального значения. Следовательно, максимальное напряжение присутствует на каждом элементе этой цепи в резонансе.

Ток, протекающий через резистор

Ток, протекающий через резистор

$$I_R = \ frac {V} {R}$$

Подставим значение V в приведенное выше уравнение.

$$I_R = \ frac {IR} {R}$$

$$\ Rightarrow I_R = I$$

Следовательно, ток, протекающий через резистор в резонансе, составляет $\ mathbf {\ mathit {I_R = I}}$.

Ток, протекающий через индуктор

Ток, протекающий через индуктор

$$I_L = \ frac {V} {j X_L}$$

Подставим значение V в приведенное выше уравнение.

$$I_L = \ frac {IR} {j X_L}$$

$$\ Rightarrow I_L = -j \ lgroup \ frac {R} {X_L} \ rgroup I$$

$$\ Rightarrow I_L = -jQI$$

Следовательно, ток, протекающий через индуктор в резонансе, равен $I_L = -jQI$.

Итак, величина тока, протекающего через индуктор в резонансе, будет

$$ | I_L | = QI $$

Где Q — фактор качества, а его значение равно $\ frac {R} {X_L}$

Ток, протекающий через конденсатор

Ток, протекающий через конденсатор

$$I_C = \ frac {V} {- j X_C}$$

Подставим значение V в приведенное выше уравнение.

$$I_C = \ frac {IR} {- j X_C}$$

$$\ Rightarrow I_C = j \ lgroup \ frac {R} {X_C} \ rgroup I$$

$$\ Rightarrow I_C = jQI$$

Следовательно, ток, протекающий через конденсатор в резонансе, составляет $I_C = jQI$.

Таким образом, величина тока, протекающего через конденсатор при резонансе, будет

$$ | I_C | = QI $$

Где Q — фактор качества, а его значение равно $\ frac {R} {X_C}$

Примечание. Схема RLC с параллельным резонансом называется схемой увеличения тока. Потому что величина тока, протекающего через индуктор и конденсатор, равна Q, умноженному на входной синусоидальный ток I.