Теорема выборки сигналов

Утверждение: непрерывный сигнал времени может быть представлен в его выборках и может быть восстановлен обратно, когда частота дискретизации f _s больше или равна удвоенной наибольшей частотной составляющей сигнала сообщения. т.е.

$$ f_s \ geq 2 f_m. $$

Доказательство: рассмотрим непрерывный сигнал времени x (t). Спектр x (t) представляет собой полосу, ограниченную f _m Гц, т. Е. Спектр x (t) равен нулю при | ω |> ω _m .

Выборка входного сигнала x (t) может быть получена умножением x (t) на последовательность импульсов δ (t) периода T _s . Выход умножителя представляет собой дискретный сигнал, называемый дискретизированным сигналом, который представлен с помощью y (t) на следующих диаграммах:

Здесь вы можете наблюдать, что дискретизированный сигнал принимает период импульса. Процесс отбора проб можно объяснить следующим математическим выражением:

$ \ text {семплированный сигнал} \, y (t) = x (t). \ delta (t) \, \, … \, … (1) $

Тригонометрическое представление ряда Фурье для $\ delta$ (t) дается

 delta(t)=a0+ Sigma inftyn=1(an cosn omegast+bn sinn omegast)... ,...(2)$\ delta (t) = a_0 + \ Sigma_ {n = 1} ^ {\ infty} (a_n \ cos⁡ n \ omega_s t + b_n \ sin⁡ n \ omega_s t) \, \, ... \ ,. .. (2)$

Где $a_0 = {1 \ over T_s} \ int _ {- T \ over 2} ^ {T \ over 2} \ delta (t) dt = {1 \ over T_s} \ delta (0) = {1 \ over T_s }$

an=2 overTs intT over2−T over2 delta(t) cosn omegasdt=2 overT2 delta(0) cosn omegas0=2 overT$a_n = {2 \ over T_s} \ int _ {- T \ over 2} ^ {T \ over 2} \ delta (t) \ cos n \ omega_s \, dt = {2 \ over T_2} \ delta (0) \ cos n \ omega_s 0 = {2 \ over T}$

bn=2 overTs intT over2−T over2 delta(t) sinn omegastdt=2 overTs delta(0) sinn omegas0=0$b_n = {2 \ over T_s} \ int _ {- T \ over 2} ^ {T \ over 2} \ delta (t) \ sin⁡ n \ omega_s t \, dt = {2 \ over T_s} \ delta ( 0) \ sin⁡ n \ omega_s 0 = 0$

Подставьте вышеуказанные значения в уравнение 2.

 следовательно delta(t)=1 overTs+ Sigma inftyn=1(2 overTs cosn omegast+0)$\ следовательно \, \ delta (t) = {1 \ over T_s} + \ Sigma_ {n = 1} ^ {\ infty} ({2 \ over T_s} \ cos ⁡ n \ omega_s t + 0)$

Подставим δ (t) в уравнение 1.

$ \ to y (t) = x (t). \ delta (t) $

$= x (t) [{1 \ over T_s} + \ Sigma_ {n = 1} ^ {\ infty} ({2 \ over T_s} \ cos n \ omega_s t)]$

$= {1 \ over T_s} [x (t) + 2 \ Sigma_ {n = 1} ^ {\ infty} (\ cos n \ omega_s t) x (t)]$

y(t)=1 overTs[x(t)+2 cos omegastx(t)+2 cos2 omegast.x(t)+2 cos3 omegastx(t)......]$y (t) = {1 \ over T_s} [x (t) + 2 \ cos \ omega_s tx (t) + 2 \ cos 2 \ omega_st.x (t) + 2 \ cos 3 \ omega_s tx (t) \, ... \, ... \,]$

Возьмите преобразование Фурье с обеих сторон.

Y( omega)=1 overTs[X( omega)+X( omega− omegas)+X( omega+ omegas)+X( omega−2 omegas)+X( omega+2 omegas)+...]$Y (\ omega) = {1 \ over T_s} [X (\ omega) + X (\ omega- \ omega_s) + X (\ omega + \ omega_s) + X (\ omega-2 \ omega_s) + X (\ omega + 2 \ omega_s) + \, ...]$

 следовательноY( omega)=1 overTs Sigma inftyn=− inftyX( omega−n omegas) quad quadгде ,n=0, pm1, pm2,...$\ следовательно \, \, Y (\ omega) = {1 \ over T_s} \ Sigma_ {n = - \ infty} ^ {\ infty} X (\ omega - n \ omega_s) \ quad \ quad где \, \ , n = 0, \ pm1, \ pm2, ...$

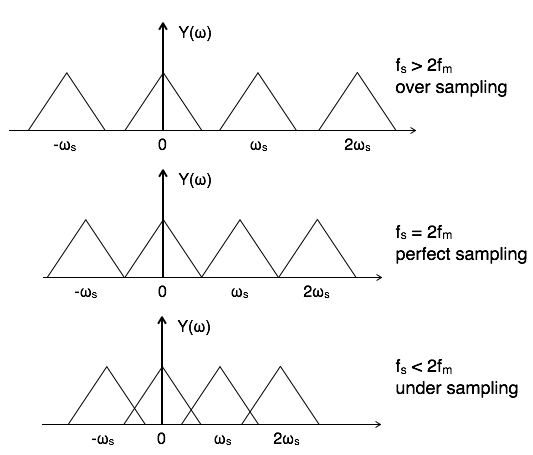
Чтобы восстановить x (t), необходимо восстановить спектр входного сигнала X (ω) из спектра дискретизированного сигнала Y (ω), что возможно, когда нет перекрытия между циклами Y (ω).

Возможность выборки частотного спектра с различными условиями дает следующие диаграммы:

Эффект сглаживания

Перекрывающаяся область в случае недостаточной выборки представляет собой эффект наложения, который может быть удален

учитывая f _s > 2f _m

Используя фильтры сглаживания.