Изменение диапазона σ, для которого сходится преобразование Лапласа, называется областью сходимости.
Свойства РПЦ преобразования Лапласа
-
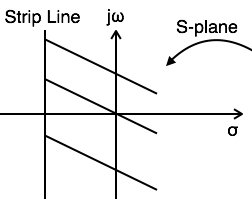
ROC содержит линии полосы, параллельные оси jω в s-плоскости.
-
Если x (t) абсолютно целое и имеет конечную длительность, то ROC является целой s-плоскостью.
-
Если x (t) — правосторонняя последовательность, то ROC: Re {s}> σ o .
-
Если x (t) является левой стороной последовательности, то ROC: Re {s} <σ o .
-
Если x (t) является двусторонней последовательностью, то ROC является комбинацией двух областей.
ROC содержит линии полосы, параллельные оси jω в s-плоскости.
Если x (t) абсолютно целое и имеет конечную длительность, то ROC является целой s-плоскостью.
Если x (t) — правосторонняя последовательность, то ROC: Re {s}> σ o .
Если x (t) является левой стороной последовательности, то ROC: Re {s} <σ o .
Если x (t) является двусторонней последовательностью, то ROC является комбинацией двух областей.
ROC можно объяснить, используя приведенные ниже примеры:
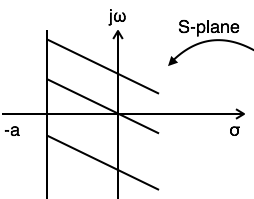
Пример 1: Найти преобразование Лапласа и ROC x(t)=e−atu(t)
LT[x(t)]=LT[e−atu(t)]=1 overS+a
Re gt−a
ROC:Res gt>−a
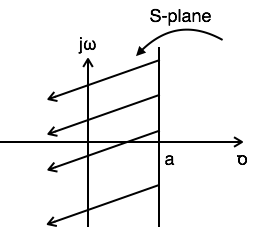
Пример 2: Найти преобразование Лапласа и ROC x(t)=eatu(−t)
LT[x(t)]=LT[eatu(t)]=1 overSa
Res<a
ROC:Res<a
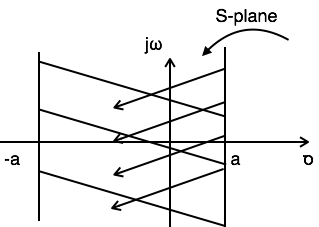
Пример 3: Найти преобразование Лапласа и ROC x(t)=e−atu(t)+eatu(−t)
LT[x(t)]=LT[e−atu(t)+eatu(−t)]=1 overS+a+1 overSa
Для {1 \ over S + a} Re \ {s \} \ gt -a
Для {1 \ over Sa} Re \ {s \} \ lt a
Ссылаясь на вышеприведенную диаграмму, область комбинации лежит от –a до a. Следовательно,
ROC:−a<Res<a
Чтобы система была причинной, все полюсы ее передаточной функции должны быть в правой половине s-плоскости.
Система называется устойчивой, когда все полюсы ее передаточной функции лежат в левой половине s-плоскости.
Говорят, что система нестабильна, когда хотя бы один полюс ее передаточной функции смещен в правую половину s-плоскости.
Система называется предельно устойчивой, когда хотя бы один полюс ее передаточной функции лежит на оси j в s-плоскости.