Свойства Z-Преобразований

Z-Transform обладает следующими свойствами:

Свойство линейности

Если x(n) stackrel mathrmZT longleftrightarrowX(Z)$\, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z)$

и y(n) stackrel mathrmZT longleftrightarrowY(Z)$\, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z)$

Тогда свойство линейности утверждает, что

ax(n)+by(n) stackrel mathrmZT longleftrightarrowaX(Z)+bY(Z)$a \, x (n) + b \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} a \, X (Z) + b \, Y (Z)$

Time Shifting Свойство

Если x(n) stackrel mathrmZT longleftrightarrowX(Z)$\, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z)$

Тогда свойство сдвига во времени утверждает, что

$x (nm) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} z ^ {- m} X (Z)$

Умножение на свойство экспоненциальной последовательности

Если x(n) stackrel mathrmZT longleftrightarrowX(Z)$\, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z)$

Тогда умножение на свойство экспоненциальной последовательности гласит, что

$ a ^ n \,. x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z / a) $

Свойство Обратного Времени

Если x(n) stackrel mathrmZT longleftrightarrowX(Z)$\, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z)$

Тогда свойство обращения времени утверждает, что

$x (-n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (1 / Z)$

Дифференцирование в Z-домене ИЛИ Умножение на n Свойство

Если x(n) stackrel mathrmZT longleftrightarrowX(Z)$\, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z)$

Тогда умножение на n или дифференцирование в свойстве z-домена утверждает, что

$n ^ kx (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} [-1] ^ kz ^ k {d ^ k X (Z) \ over dZ ^ K}$

Собственность свертки

Если x(n) stackrel mathrmZT longleftrightarrowX(Z)$\, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z)$

и y(n) stackrel mathrmZT longleftrightarrowY(Z)$\, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z)$

Тогда свойство свертки утверждает, что

$x (n) * y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z)$

Свойство корреляции

Если x(n) stackrel mathrmZT longleftrightarrowX(Z)$\, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z)$

и y(n) stackrel mathrmZT longleftrightarrowY(Z)$\, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z)$

Тогда свойство корреляции утверждает, что

$x (n) \ otimes y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z ^ {- 1})$

Начальные и конечные значения теорем

Теоремы о начальном и конечном значении z-преобразования определены для причинного сигнала.

Теорема начального значения

Для причинного сигнала x (n) теорема начального значения утверждает, что

x(0)= limz to inftyX(z)$x (0) = \ lim_ {z \ to \ infty} ⁡X (z)$

Это используется для определения начального значения сигнала без обратного z-преобразования.

Окончательная Теорема Значения

Для причинного сигнала x (n) теорема об окончательном значении утверждает, что

x( infty)= limz to1[z−1]X(z)$x (\ infty) = \ lim_ {z \ to 1} [z-1] ⁡X (z)$

Это используется, чтобы найти окончательное значение сигнала без обратного z-преобразования.

Область сходимости (ROC) Z-Transform

Диапазон изменения z, для которого сходится z-преобразование, называется областью сходимости z-преобразования.

Свойства РПЦ Z-преобразований

• ROC z-преобразования обозначается кружком в z-плоскости.

• РПЦ не содержит никаких полюсов.

• Если x (n) является причинной последовательностью конечной продолжительности или правосторонней последовательностью, то ROC является целой z-плоскостью за исключением z = 0.

• Если x (n) является антикаузальной последовательностью конечной продолжительности или левой стороной последовательности, то ROC является целой z-плоскостью за исключением z = ∞.

• Если x (n) — причинная последовательность бесконечной продолжительности, ROC является внешней от окружности с радиусом aie | z | > а.

• Если x (n) — антикаузальная последовательность бесконечной продолжительности, ROC — внутренняя часть круга с радиусом aie | z | <а.

• Если x (n) — двусторонняя последовательность конечной длительности, то ROC является целой z-плоскостью за исключением z = 0 и z = ∞.

ROC z-преобразования обозначается кружком в z-плоскости.

РПЦ не содержит никаких полюсов.

Если x (n) является причинной последовательностью конечной продолжительности или правосторонней последовательностью, то ROC является целой z-плоскостью за исключением z = 0.

Если x (n) является антикаузальной последовательностью конечной продолжительности или левой стороной последовательности, то ROC является целой z-плоскостью за исключением z = ∞.

Если x (n) — причинная последовательность бесконечной продолжительности, ROC является внешней от окружности с радиусом aie | z | > а.

Если x (n) — антикаузальная последовательность бесконечной продолжительности, ROC — внутренняя часть круга с радиусом aie | z | <а.

Если x (n) — двусторонняя последовательность конечной длительности, то ROC является целой z-плоскостью за исключением z = 0 и z = ∞.

Концепция ROC может быть объяснена следующим примером:

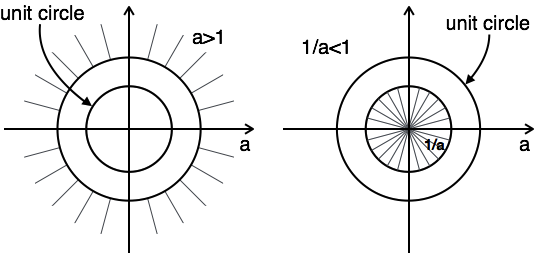
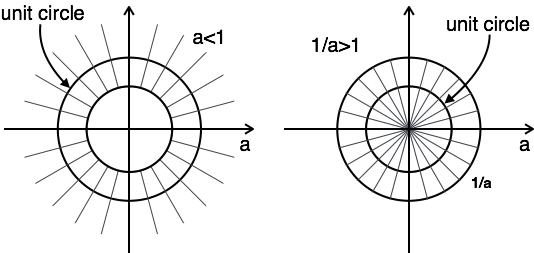
Пример 1: Найти z-преобразование и ROC $a ^ nu [n] + a ^ {-} nu [-n-1]$

$ZT [a ^ nu [n]] + ZT [a ^ {- n} u [-n-1]] = {Z \ over Za} + {Z \ over Z {-1 \ over a}}$

$$ ROC: | z | \ gt a \ quad \ quad ROC: | z | \ lt {1 \ over a} $$

Сюжет ROC имеет два условия как> 1 и <1, как вы не знаете, а.

В этом случае нет комбинации ROC.

Здесь комбинация ROC из $ a \ lt | z | \ lt {1 \ over a} $

Следовательно, для этой задачи z-преобразование возможно, когда a <1.

Причинность и стабильность

Условие причинности для систем LTI с дискретным временем следующее:

Система LTI с дискретным временем является

• РПЦ находится за пределами самого внешнего полюса.

• В передаточной функции H [Z] порядок числителя не может быть больше, чем порядок знаменателя.

РПЦ находится за пределами самого внешнего полюса.

В передаточной функции H [Z] порядок числителя не может быть больше, чем порядок знаменателя.

Условие стабильности для систем LTI с дискретным временем

Система LTI с дискретным временем стабильна, когда

его системная функция H [Z] включает единичную окружность | z | = 1.

все полюсы передаточной функции лежат внутри единичного круга | z | = 1.