Преобразования Фурье

Основным недостатком ряда Фурье является то, что он применим только к периодическим сигналам. Существуют естественные сигналы, такие как непериодические или апериодические, которые мы не можем представить с помощью рядов Фурье. Чтобы преодолеть этот недостаток, Фурье разработал математическую модель для преобразования сигналов между временной (или пространственной) областью в частотную область и наоборот, которая называется «преобразованием Фурье».

Преобразование Фурье имеет множество применений в физике и технике, таких как анализ систем LTI, RADAR, астрономия, обработка сигналов и т. Д.

Вывод преобразования Фурье из ряда Фурье

Рассмотрим периодический сигнал f (t) с периодом T. Представление комплексного ряда Фурье для f (t) задается как

$$ f (t) = \ sum_ {k = — \ infty} ^ {\ infty} a_k e ^ {jk \ omega_0 t} $$

$$ \ quad \ quad \ quad \ quad \ quad = \ sum_ {k = — \ infty} ^ {\ infty} a_k e ^ {j {2 \ pi \ over T_0} kt} … … (1 ) $$

Пусть $ {1 \ over T_0} = \ Delta f $, тогда уравнение 1 становится

$ f (t) = \ sum_ {k = — \ infty} ^ {\ infty} a_k e ^ {j2 \ pi k \ Delta ft} … … (2) $

но ты знаешь что

$ a_k = {1 \ over T_0} \ int_ {t_0} ^ {t_0 + T} f (t) e ^ {- jk \ omega_0 t} dt $

$ a_k = {1 \ over T_0} \ int_ {t_0} ^ {t_0 + T} f (t) e ^ {- jk \ omega_0 t} dt $

Подставим в уравнение 2.

(2) $ \ Rightarrow f (t) = \ Sigma_ {k = — \ infty} ^ {\ infty} {1 \ over T_0} \ int_ {t_0} ^ {t_0 + T} f (t) e ^ {- jk \ omega_0 t} dt \, e ^ {j2 \ pi k \ Delta ft} $

Пусть $ t_0 = {T \ over2} $

$ = \ Sigma_ {k = — \ infty} ^ {\ infty} [\ int _ {- T \ over2} ^ {T \ over2} f (t) e ^ {- j2 \ pi k \ Delta ft} dt] \ , e ^ {j2 \ pi k \ Delta ft}. \ Delta f $

В пределе, когда $ T \ to \ infty, \ Delta f $ приближается к дифференциалу $ df, k \ Delta f $ становится непрерывной переменной $ f $, а суммирование становится интегрированием

$$ f (t) = lim_ {T \ to \ infty} ⁡ \ left \ {\ Sigma_ {k = — \ infty} ^ {\ infty} [\ int _ {- T \ over2} ^ {T \ over2} f (t) e ^ {- j2 \ pi k \ Delta ft} dt] \, e ^ {j2 \ pi k \ Delta ft}. \ Delta f \ right \} $$

$$ = \ int _ {- \ infty} ^ {\ infty} [\ int _ {- \ infty} ^ {\ infty} \, f (t) e ^ {- j2 \ pi ft} dt] e ^ {j2 \ pi ft} df $$

$$ f (t) = \ int _ {- \ infty} ^ {\ infty} \, F [\ omega] e ^ {j \ omega t} d \ omega $$

$ \ text {Where} \, F [\ omega] = [\ int _ {- \ infty} ^ {\ infty} \, f (t) e ^ {- j2 \ pi ft} dt] $

Преобразование Фурье сигнала $$ f (t) = F [\ omega] = [\ int _ {- \ infty} ^ {\ infty} \, f (t) e ^ {- j \ omega t} dt] $$

Обратное преобразование Фурье имеет вид $$ f (t) = \ int _ {- \ infty} ^ {\ infty} \, F [\ omega] e ^ {j \ omega t} d \ omega $$

Преобразование Фурье основных функций

Давайте пройдемся по преобразованию Фурье основных функций:

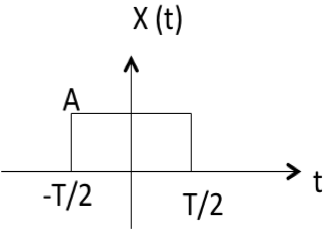
FT функции GATE

$$ F [\ omega] = AT Sa ({\ omega T \ over 2}) $$

FT импульсной функции

$ FT [\ omega (t)] = [\ int _ {- \ infty} ^ {\ infty} \ delta (t) e ^ {- j \ omega t} dt] $

$ \ quad \ quad \ quad \ quad = e ^ {- j \ omega t} \, | \, t = 0 $

$ \ quad \ quad \ quad \ quad = e ^ {0} = 1 $

$ \ quad \ следовательно \ delta (\ omega) = 1 $

FT функции шага блока:

$ U (\ omega) = \ pi \ delta (\ omega) + 1 / j \ omega $

FT экспоненциальных

$ e ^ {- at} u (t) \ stackrel {\ mathrm {FT}} {\ longleftrightarrow} 1 / (a ​​+ jω) $

$ e ^ {- at} u (t) \ stackrel {\ mathrm {FT}} {\ longleftrightarrow} 1 / (a ​​+ j \ omega) $

$ e ^ {- a \, | \, t \, |} \ stackrel {\ mathrm {FT}} {\ longleftrightarrow} {2a \ over {a ^ 2 + ω ^ 2}} $

$ e ^ {j \ omega_0 t} \ stackrel {\ mathrm {FT}} {\ longleftrightarrow} \ delta (\ omega — \ omega_0) $

FT функции Signum

$ sgn (t) \ stackrel {\ mathrm {FT}} {\ longleftrightarrow} {2 \ over j \ omega} $

Условия существования преобразования Фурье

Любая функция f (t) может быть представлена ​​с помощью преобразования Фурье только тогда, когда функция удовлетворяет условиям Дирихле. т.е.

• Функция f (t) имеет конечное число максимумов и минимумов.

• Должно быть конечное число разрывов в сигнале f (t) в заданном интервале времени.

• Он должен быть абсолютно интегрируемым в данном интервале времени, т.е.

  $ \ int _ {- \ infty} ^ {\ infty} \, | \, f (t) | \, dt <\ infty $

Функция f (t) имеет конечное число максимумов и минимумов.

Должно быть конечное число разрывов в сигнале f (t) в заданном интервале времени.

Он должен быть абсолютно интегрируемым в данном интервале времени, т.е.

$ \ int _ {- \ infty} ^ {\ infty} \, | \, f (t) | \, dt <\ infty $

Дискретные преобразования времени Фурье (DTFT)

Дискретное преобразование Фурье (DTFT) или преобразование Фурье для последовательности с дискретным временем x [n] является представлением последовательности в терминах комплексной экспоненциальной последовательности $ e ^ {j \ omega n} $.

DTFT-последовательность x [n] задается как

$$ X (\ omega) = \ Sigma_ {n = — \ infty} ^ {\ infty} x (n) e ^ {- j \ omega n} \, \, … \, … (1) $$

Здесь X (ω) является комплексной функцией действительной частотной переменной ω, и ее можно записать в виде

$$ X (\ omega) = X_ {re} (\ omega) + jX_ {img} (\ omega) $$

Где X _re (ω), X _img (ω) — действительная и мнимая части X (ω) соответственно.

$$ X_ {re} (\ omega) = | \, X (\ omega) | \ cos \ theta (\ omega) $$

$$ X_ {img} (\ omega) = | \, X (\ omega) | \ sin \ theta (\ omega) $$

$$ | X (\ omega) | ^ 2 = | \, X_ {re} (\ omega) | ^ 2 + | \, X_ {im} (\ omega) | ^ 2 $$

И X (ω) также можно представить как $ X (\ omega) = | \, X (\ omega) | e ^ {j \ theta (ω)} $

Где $ \ theta (\ omega) = arg {X (\ omega)} $

$ | \, X (\ omega) |, \ theta (\ omega) $ называются амплитудными и фазовыми спектрами X (ω).

Обратное преобразование Фурье с дискретным временем

$$ x (n) = {1 \ over 2 \ pi} \ int _ {- \ pi} ^ {\ pi} X (\ omega) e ^ {j \ omega n} d \ omega \, \, … \, … (2) $$

Условие сходимости:

Бесконечный ряд в уравнении 1 может сходиться или не сходиться. x (n) абсолютно суммируемо.

$$ \ text {when} \, \, \ sum_ {n = — \ infty} ^ {\ infty} | \, x (n) | \, <\ infty $$

Абсолютно суммируемая последовательность всегда имеет конечную энергию, но последовательность с конечной энергией не обязательно должна быть абсолютно суммируемой.