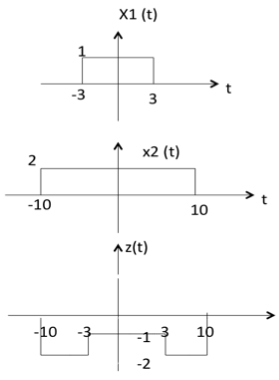Сигналы Основные операции

В общем, есть два переменных параметра:

1. амплитудное
2. Время

Следующая операция может быть выполнена с амплитудой:

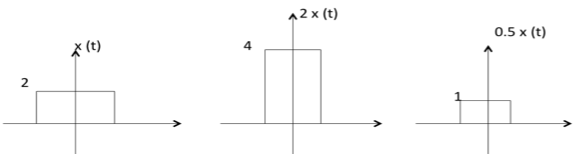
Амплитудное масштабирование

C x (t) — это масштабированная по амплитуде версия x (t), амплитуда которой масштабируется с коэффициентом C.

прибавление

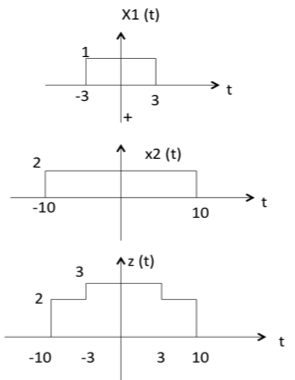
Добавление двух сигналов — не что иное, как сложение их соответствующих амплитуд. Это может быть лучше всего объяснено с помощью следующего примера:

Как видно из диаграммы выше,

-10 <t <-3 амплитуда z (t) = x1 (t) + x2 (t) = 0 + 2 = 2

-3 <t <3, амплитуда z (t) = x1 (t) + x2 (t) = 1 + 2 = 3

3 <t <10, амплитуда z (t) = x1 (t) + x2 (t) = 0 + 2 = 2

-10 <t <-3 амплитуда z (t) = x1 (t) + x2 (t) = 0 + 2 = 2

-3 <t <3, амплитуда z (t) = x1 (t) + x2 (t) = 1 + 2 = 3

3 <t <10, амплитуда z (t) = x1 (t) + x2 (t) = 0 + 2 = 2

Вычитание

вычитание двух сигналов является ничем иным, как вычитанием их соответствующих амплитуд. Это лучше всего объяснить следующим примером:

Как видно из диаграммы выше,

-10 <t <-3 амплитуда z (t) = x1 (t) — x2 (t) = 0 — 2 = -2

-3 <t <3, амплитуда z (t) = x1 (t) — x2 (t) = 1 — 2 = -1

3 <t <10, амплитуда z (t) = x1 (t) + x2 (t) = 0 — 2 = -2

-10 <t <-3 амплитуда z (t) = x1 (t) — x2 (t) = 0 — 2 = -2

-3 <t <3, амплитуда z (t) = x1 (t) — x2 (t) = 1 — 2 = -1

3 <t <10, амплитуда z (t) = x1 (t) + x2 (t) = 0 — 2 = -2

умножение

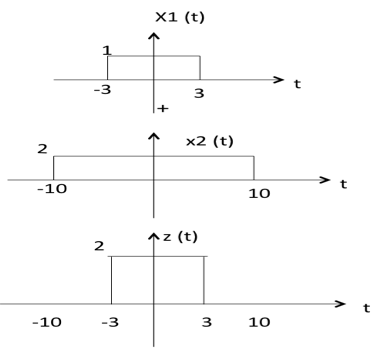
Умножение двух сигналов — не что иное, как умножение их соответствующих амплитуд. Это лучше всего объяснить следующим примером:

Как видно из диаграммы выше,

-10 <t <-3 амплитуда z (t) = x1 (t) × x2 (t) = 0 × 2 = 0

-3 <t <3, амплитуда z (t) = x1 (t) × x2 (t) = 1 × 2 = 2

3 <t <10, амплитуда z (t) = x1 (t) × x2 (t) = 0 × 2 = 0

-10 <t <-3 амплитуда z (t) = x1 (t) × x2 (t) = 0 × 2 = 0

-3 <t <3, амплитуда z (t) = x1 (t) × x2 (t) = 1 × 2 = 2

3 <t <10, амплитуда z (t) = x1 (t) × x2 (t) = 0 × 2 = 0

Следующие операции могут быть выполнены со временем:

Временной сдвиг

x (t $ \ pm $ t ₀ ) — сдвинутая по времени версия сигнала x (t).

x (t + t ₀ ) $ \ to $ отрицательный сдвиг

x (t — t ₀ ) $ \ to $ положительное смещение

x (t + t ₀ ) $ \ to $ отрицательный сдвиг

x (t — t ₀ ) $ \ to $ положительное смещение

Масштабирование времени

x (At) — масштабированная по времени версия сигнала x (t). где А всегда положительно.

| | > 1 $ \ to $ Сжатие сигнала

| | <1 $ \ to $ Расширение сигнала

| | > 1 $ \ to $ Сжатие сигнала

| | <1 $ \ to $ Расширение сигнала

Примечание: u (at) = u (t) масштабирование времени не применимо для функции единичного шага.

Обратное время

x (-t) — время обращения сигнала x (t).