Методы выборки сигналов

Существует три типа методов отбора проб:

• Импульсная выборка.

• Естественная выборка.

• Фронтальная выборка.

Импульсная выборка.

Естественная выборка.

Фронтальная выборка.

Импульсная выборка

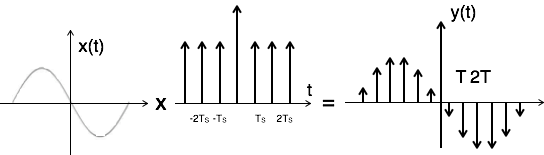
Импульсная выборка может быть выполнена путем умножения входного сигнала x (t) на импульсную последовательность $\ Sigma_ {n = - \ infty} ^ {\ infty} \ delta (t-nT)$ периода ‘T’. Здесь амплитуда импульса изменяется по отношению к амплитуде входного сигнала x (t). Выход сэмплера определяется как

$y (t) = x (t) ×$ импульсный поезд

$= x (t) × \ Sigma_ {n = - \ infty} ^ {\ infty} \ delta (t-nT)$

y(t)=y delta(t)= Sigma inftyn=− inftyx(nt) delta(t−nT)......1$y (t) = y _ {\ delta} (t) = \ Sigma_ {n = - \ infty} ^ {\ infty} x (nt) \ delta (t-nT) \, ... \, ... 1$

Чтобы получить спектр дискретизированного сигнала, рассмотрим преобразование Фурье уравнения 1 с обеих сторон.

$Y (\ omega) = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} X (\ omega - n \ omega_s)$

Это называется идеальной выборкой или импульсной выборкой. Вы не можете использовать это практически, потому что ширина импульса не может быть нулевой, а генерация последовательности импульсов практически невозможна.

Естественная выборка

Естественная выборка аналогична импульсной выборке, за исключением того, что импульсная последовательность заменяется импульсной последовательностью периода Т. Т.е. вы умножаете входной сигнал x (t) на импульсную последовательность $\ Sigma_ {n = - \ infty} ^ {\ infty} P ( t-nT)$, как показано ниже

Выход сэмплера

$y (t) = x (t) \ times \ text {последовательность импульсов}$

$= x (t) \ times p (t)$

=x(t) times Sigma inftyn=− inftyP(t−nT)......(1)$= x (t) \ times \ Sigma_ {n = - \ infty} ^ {\ infty} P (t-nT) \, ... \, ... (1)$

Экспоненциальное представление ряда Фурье для p (t) может быть задано как

p(t)= Sigma inftyn=− inftyFnejn omegast......(2)$p (t) = \ Sigma_ {n = - \ infty} ^ {\ infty} F_n e ^ {jn \ omega_s t} \, ... \, ... (2)$

$= \ Sigma_ {n = - \ infty} ^ {\ infty} F_n e ^ {j 2 \ pi nf_s t}$

Где $F_n = {1 \ over T} \ int _ {- T \ over 2} ^ {T \ over 2} p (t) e ^ {- jn \ omega_s t} dt$

$= {1 \ over TP} (n \ omega_s)$

Подставим значение F _n в уравнение 2

$\ следовательно p (t) = \ Sigma_ {n = - \ infty} ^ {\ infty} {1 \ over T} P (n \ omega_s) e ^ {jn \ omega_s t}$

$= {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) e ^ {jn \ omega_s t}$

Подставим p (t) в уравнение 1

$y (t) = x (t) \ times p (t)$

=x(t) times1 overT Sigma inftyn=− inftyP(n omegas)ejn omegast$= x (t) \ times {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, e ^ {jn \ omega_s t}$

y(t)=1 overT Sigma inftyn=− inftyP(n omegas)x(t)ejn omegast$y (t) = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, x (t) \, e ^ {jn \ omega_s t}$

Чтобы получить спектр дискретизированного сигнала, рассмотрим преобразование Фурье с обеих сторон.

FT[y(t)]=FT[1 overT Sigma inftyn=− inftyP(n omegas)x(t)ejn omegast]$FT \, [y (t)] = FT [{1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, x (t) \, e ^ { jn \ omega_s t}]$

=1 overT Sigma inftyn=− inftyP(n omegas)FT[x(t)ejn omegast]$= {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, FT \, [x (t) \, e ^ {jn \ omega_s t}]$

По частоте сдвига

FT[x(t)ejn omegast]=X[ omega−n omegas]$FT \, [x (t) \, e ^ {jn \ omega_s t}] = X [\ omega-n \ omega_s]$

 следовательноY[ omega]=1 overT Sigma inftyn=− inftyP(n omegas)X[ omega−n omegas]$\ следовательно \, Y [\ omega] = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, X [\ omega-n \ omega_s]$

Отбор проб с плоской вершиной

Во время передачи шум вводится в верхней части импульса передачи, который может быть легко удален, если импульс имеет форму плоской вершины. Здесь верхняя часть образцов является плоской, то есть они имеют постоянную амплитуду. Следовательно, это называется выборкой с плоским верхом или практической выборкой. Для выборки с плоским верхом используется схема выборки и удержания.

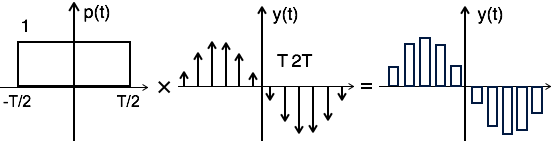
Теоретически, дискретизированный сигнал может быть получен путем свертки прямоугольного импульса p (t) с идеально дискретизированным сигналом, скажем, y _δ (t), как показано на схеме:

то есть y(t)=p(t) timesy delta(t)......(1)$y (t) = p (t) \ times y_ \ delta (t) \, ... \, ... (1)$

Чтобы получить выборочный спектр, рассмотрим преобразование Фурье с обеих сторон для уравнения 1

Y[ omega]=FT[P(t) timesy delta(t)]$Y [\ omega] = FT \, [P (t) \ times y_ \ delta (t)]$

По знанию свойства свертки,

Y[ omega]=P( omega)Y delta( omega)$Y [\ omega] = P (\ omega) \, Y_ \ delta (\ omega)$

Здесь $P (\ omega) = T Sa ({\ omega T \ over 2}) = 2 \ sin \ omega T / \ omega$

Рейтинг Найквиста

Это минимальная частота дискретизации, при которой сигнал может быть преобразован в выборки и может быть восстановлен без искажений.

Частота Найквиста f _N = 2f _м Гц

Интервал Найквиста = ${1 \ over fN}$ = ${1 \ over 2fm}$ секунд.

Выборки полосовых сигналов

В случае полосовых сигналов спектр полосового сигнала X [ω] = 0 для частот вне диапазона f ₁ ≤ f ≤ f ₂ . Частота f ₁ всегда больше нуля. Кроме того, эффект псевдонима отсутствует, если f _s > 2f ₂ . Но у него есть два недостатка:

• Частота дискретизации велика пропорционально f ₂ . Это имеет практические ограничения.

• Спектр дискретизированного сигнала имеет спектральные промежутки.

Частота дискретизации велика пропорционально f ₂ . Это имеет практические ограничения.

Спектр дискретизированного сигнала имеет спектральные промежутки.

Чтобы преодолеть это, теорема о полосе пропускания утверждает, что входной сигнал x (t) может быть преобразован в его выборки и может быть восстановлен обратно без искажений при частоте дискретизации f _s <2f ₂ .

Также,

$$f_s = {1 \ over T} = {2f_2 \ over m}$$

Где m — наибольшее целое число <${f_2 \ over B}$

и B — ширина полосы сигнала. Если f ₂ = КБ, то

$$f_s = {1 \ over T} = {2KB \ over m}$$

Для полосовых сигналов с шириной полосы 2f _m и минимальной частотой дискретизации f _s = 2 B = 4f _m ,

спектр дискретизированного сигнала определяется как Y[ omega]=1 overT Sigma inftyn=− inftyX[ omega−2nB]$Y [\ omega] = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} \, X [\ omega - 2nB]$