Свертка и корреляция

Свертка — это математическая операция, используемая для выражения связи между входом и выходом системы LTI. Он связывает вход, выход и импульсную характеристику системы LTI как

$$y (t) = x (t) * h (t)$$

Где у (т) = выходной LTI

х (т) = ввод LTI

h (t) = импульсный отклик LTI

Есть два типа извилин:

• Непрерывная свертка

• Дискретная свертка

Непрерывная свертка

Дискретная свертка

Непрерывная свертка

y(t)=x(t)∗h(t)$y (t) \, \, = x (t) * h (t)$

$= \ int _ {- \ infty} ^ {\ infty} x (\ tau) h (t- \ tau) d \ tau$

(или же)

$= \ int _ {- \ infty} ^ {\ infty} x (t - \ tau) h (\ tau) d \ tau$

Дискретная свертка

y(n)=x(n)∗h(n)$y (n) \, \, = x (n) * h (n)$

$= \ Sigma_ {k = - \ infty} ^ {\ infty} x (k) h (nk)$

(или же)

$= \ Sigma_ {k = - \ infty} ^ {\ infty} x (nk) h (k)$

Используя свертку, мы можем найти отклик системы в нулевом состоянии.

деконволюция

Деконволюция — это процесс, обратный процессу свертки, широко используемый в обработке сигналов и изображений.

Свойства свертки

Коммутативная собственность

$x_1 (t) * x_2 (t) = x_2 (t) * x_1 (t)$

Распределительное свойство

$x_1 (t) * [x_2 (t) + x_3 (t)] = [x_1 (t) * x_2 (t)] + [x_1 (t) * x_3 (t)]$

Ассоциативная собственность

$x_1 (t) * [x_2 (t) * x_3 (t)] = [x_1 (t) * x_2 (t)] * x_3 (t)$

Сдвиг собственности

$x_1 (t) * x_2 (t) = y (t)$

$x_1 (t) * x_2 (t-t_0) = y (t-t_0)$

$x_1 (t-t_0) * x_2 (t) = y (t-t_0)$

$x_1 (t-t_0) * x_2 (t-t_1) = y (t-t_0-t_1)$

Свертка с импульсом

$x_1 (t) * \ delta (t) = x (t)$

$x_1 (t) * \ delta (t- t_0) = x (t-t_0)$

Свертка шагов ступени

$u (t) * u (t) = r (t)$

$u (t-T_1) * u (t-T_2) = r (t-T_1-T_2)$

$u (n) * u (n) = [n + 1] u (n)$

Свойство масштабирования

Если $x (t) * h (t) = y (t)$

тогда $x (at) * h (at) = {1 \ over | a |} y (at)$

Дифференциация выпуска

если $y (t) = x (t) * h (t)$

тогда ${dy (t) \ over dt} = {dx (t) \ over dt} * h (t)$

или же

${dy (t) \ over dt} = x (t) * {dh (t) \ over dt}$

Замечания:

• Свертка двух причинных последовательностей является причинной.

• Свертка двух анти-причинных последовательностей является анти-каузальной.

• Свертывание двух прямоугольников неравной длины приводит к трапеции.

• Свертывание двух прямоугольников одинаковой длины приводит к треугольнику.

• Свернутая функция сама по себе равна интеграции этой функции.

Свертка двух причинных последовательностей является причинной.

Свертка двух анти-причинных последовательностей является анти-каузальной.

Свертывание двух прямоугольников неравной длины приводит к трапеции.

Свертывание двух прямоугольников одинаковой длины приводит к треугольнику.

Свернутая функция сама по себе равна интеграции этой функции.

Пример: вы знаете, что $u (t) * u (t) = r (t)$

Согласно приведенному выше примечанию, $u (t) * u (t) = \ int u (t) dt = \ int 1dt = t = r (t)$

Здесь вы получаете результат, просто интегрируя $u (t)$.

Пределы замысловатого сигнала

Если два сигнала свернуты, то результирующий извилистый сигнал имеет следующий диапазон:

Сумма нижних пределов <t <сумма верхних пределов

Пример: найти диапазон свертки сигналов, приведенных ниже

Здесь у нас есть два прямоугольника неравной длины, чтобы свернуть, что приводит к трапеции.

Диапазон извилистого сигнала:

Сумма нижних пределов <t <сумма верхних пределов

$-1 + -2 &amp;lt;t &amp;lt;2 + 2$

$-3 &amp;lt;t &amp;lt;4$

Следовательно, результатом является трапеция с периодом 7.

Площадь извилистого сигнала

Площадь под извилистым сигналом определяется как $A_y = A_x A_h$

Где A _x = площадь под входным сигналом

A _h = площадь под импульсным откликом

A _y = площадь под выходным сигналом

Доказательство: $y (t) = \ int _ {- \ infty} ^ {\ infty} x (\ tau) h (t- \ tau) d \ tau$

Возьмите интеграцию с обеих сторон

 inty(t)dt= int int infty− inftyx( tau)h(t− tau)d taudt$\ int y (t) dt \, \, \, = \ int \ int _ {- \ infty} ^ {\ infty} \, x (\ tau) h (t- \ tau) d \ tau dt$

= intx( tau)d tau int infty− inftyh(t− tau)dt$= \ int x (\ tau) d \ tau \ int _ {- \ infty} ^ {\ infty} \, h (t- \ tau) dt$

Мы знаем, что область любого сигнала — это интеграция самого сигнала.

 следовательноAy=Ax​​Ah$\ следовательно A_y = A_x \, ​​A_h$

Компонент постоянного тока

Постоянная составляющая любого сигнала определяется

$\ text {DC component} = {\ text {область сигнала} \ over \ text {период сигнала}}$

Пример: какова постоянная составляющая результирующего извилистого сигнала, приведенного ниже?

Здесь площадь х ₁ (т) = длина × ширина = 1 × 3 = 3

площадь х ₂ (т) = длина × ширина = 1 × 4 = 4

площадь извилистого сигнала = площадь х ₁ (т) х площадь х ₂ (т)

= 3 × 4 = 12

Длительность извилистого сигнала = сумма нижних пределов <t <сумма верхних пределов

= -1 + -2 <t <2 + 2

= -3 <t <4

Период = 7

Компонент $\ следовательно$ Dc извилистого сигнала = $\ text {область сигнала} \ over \ text {период сигнала}$

Компонент постоянного тока = ${12 \ over 7}$

Дискретная свертка

Давайте посмотрим, как рассчитать дискретную свертку:

я. Для вычисления дискретной линейной свертки:

Свернутые две последовательности x [n] = {a, b, c} & h [n] = [e, f, g]

Свернутый вывод = [ea, eb + fa, ec + fb + ga, fc + gb, gc]

Примечание: если любые две последовательности имеют m, n числа выборок соответственно, то полученная извилистая последовательность будет иметь [m + n-1] выборок.

Пример: две сложные последовательности x [n] = {1,2,3} & h [n] = {-1,2,2}

Свернутый вывод y [n] = [-1, -2 + 2, -3 + 4 + 2, 6 + 4, 6]

= [-1, 0, 3, 10, 6]

Здесь x [n] содержит 3 выборки, а h [n] также имеет 3 выборки, поэтому результирующая последовательность имеет 3 + 3-1 = 5 выборок.

II. Для расчета периодической или круговой свертки:

Периодическая свертка действительна для дискретного преобразования Фурье. Для расчета периодической свертки все образцы должны быть действительными. Периодическая или круговая свертка также называется быстрой сверткой.

Если две последовательности длиной m, n соответственно свернуты с использованием круговой свертки, то результирующая последовательность имеет максимум [m, n] выборок.

Пример: свертка двух последовательностей x [n] = {1,2,3} & h [n] = {-1,2,2} с использованием круговой свертки

Нормальный свернутый выход y [n] = [-1, -2 + 2, -3 + 4 + 2, 6 + 4, 6].

= [-1, 0, 3, 10, 6]

Здесь x [n] содержит 3 образца, а h [n] также имеет 3 образца. Следовательно, полученная последовательность, полученная круговой сверткой, должна иметь максимум [3,3] = 3 выборки.

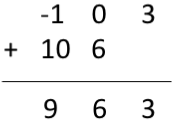
Теперь, чтобы получить результат периодической свертки, первые 3 выборки [с периодом 3] нормальной свертки совпадают, следующие две выборки добавляются к 1-м выборкам, как показано ниже:

$\ следовательно$ Результат круговой свертки $y [n] = [9 \ quad 6 \ quad 3]$

корреляция

Корреляция — это мера сходства между двумя сигналами. Общая формула для корреляции

$$\ int _ {- \ infty} ^ {\ infty} x_1 (t) x_2 (t- \ tau) dt$$

Существует два типа корреляции:

• Автокорреляция

• Cros корреляция

Автокорреляция

Cros корреляция

Функция автокорреляции

Это определяется как корреляция сигнала с самим собой. Функция автокорреляции — это мера сходства сигнала и его версии с задержкой по времени. Он представлен с помощью R ($\ tau$).

Рассмотрим сигналы x (t). Функция автокорреляции x (t) с версией с временной задержкой задается как

$$R_ {11} (\ tau) = R (\ tau) = \ int _ {- \ infty} ^ {\ infty} x (t) x (t- \ tau) dt \ quad \ quad \ text {[+ ve shift]}$$

$$\ quad \ quad \ quad \ quad \ quad = \ int _ {- \ infty} ^ {\ infty} x (t) x (t + \ tau) dt \ quad \ quad \ text {[- ve shift]}$$

Где $\ tau$ = параметр поиска или сканирования или задержки.

Если сигнал сложный, то функция автокорреляции определяется как

$$R_ {11} (\ tau) = R (\ tau) = \ int _ {- \ infty} ^ {\ infty} x (t) x * (t- \ tau) dt \ quad \ quad \ text {[ + ve shift]}$$

$$\ quad \ quad \ quad \ quad \ quad = \ int _ {- \ infty} ^ {\ infty} x (t + \ tau) x * (t) dt \ quad \ quad \ text {[- ve shift] }$$

Свойства автокорреляционной функции энергетического сигнала

• Автокорреляция проявляет сопряженную симметрию, т.е. R ($\ tau$) = R * (- $\ tau$)

• Автокорреляционная функция энергетического сигнала в начале координат, т.е. при $\ tau$ = 0, равна полной энергии этого сигнала, которая определяется как:

  R (0) = E =  int infty− infty|x(t)|2dt$\ int _ {- \ infty} ^ {\ infty} \, | \, x (t) \, | ^ 2 \, dt$

• Автокорреляционная функция $\ infty {1 \ over \ tau}$,

• Функция автокорреляции максимальна при $\ tau$ = 0, т.е. | R ($\ tau$) | ≤ R (0) ∀ $\ tau$

• Автокорреляционная функция и спектральные плотности энергии являются парами преобразования Фурье. т.е.

  FT[R( tau)]= Psi( omega)$FT \, [R (\ tau)] = \ Psi (\ omega)$

  $\ Psi (\ omega) = \ int _ {- \ infty} ^ {\ infty} R (\ tau) e ^ {- j \ omega \ tau} d \ tau$

• $R (\ tau) = x (\ tau) * x (- \ tau)$

Автокорреляция проявляет сопряженную симметрию, т.е. R ($\ tau$) = R * (- $\ tau$)

Автокорреляционная функция энергетического сигнала в начале координат, т.е. при $\ tau$ = 0, равна полной энергии этого сигнала, которая определяется как:

R (0) = E =  int infty− infty|x(t)|2dt$\ int _ {- \ infty} ^ {\ infty} \, | \, x (t) \, | ^ 2 \, dt$

Автокорреляционная функция $\ infty {1 \ over \ tau}$,

Функция автокорреляции максимальна при $\ tau$ = 0, т.е. | R ($\ tau$) | ≤ R (0) ∀ $\ tau$

Автокорреляционная функция и спектральные плотности энергии являются парами преобразования Фурье. т.е.

FT[R( tau)]= Psi( omega)$FT \, [R (\ tau)] = \ Psi (\ omega)$

$\ Psi (\ omega) = \ int _ {- \ infty} ^ {\ infty} R (\ tau) e ^ {- j \ omega \ tau} d \ tau$

$R (\ tau) = x (\ tau) * x (- \ tau)$

Автокорреляционная функция силовых сигналов

Функция автокорреляции периодического сигнала мощности с периодом T определяется как

R( tau)= limT to infty1 overT intT over2−T over2x(t)x∗(t− tau)dt $$R (\ tau) = \ lim_ {T \ to \ infty} {1 \ over T} \ int _ {{- T \ over 2}} ^ {{T \ over 2}} \, x (t) x * (t- \ tau) dt$$

свойства

• Автокорреляция сигнала мощности проявляет сопряженную симметрию, т.е. $R (\ tau) = R * (- \ tau)$

• Автокорреляционная функция сигнала мощности при $\ tau = 0$ (в начале координат) равна общей мощности этого сигнала. т.е.

  $R (0) = \ rho$

• Автокорреляционная функция сигнала мощности $\ infty {1 \ over \ tau}$,

• Автокорреляционная функция сигнала мощности максимальна при $\ tau$ = 0, т.е.

  $ | R (\ тау) | \ leq R (0) \, \ forall \, \ tau $

• Автокорреляционная функция и спектральные плотности мощности являются парами преобразования Фурье. т.е.

  $FT [R (\ tau)] = s (\ omega)$

  $s (\ omega) = \ int _ {- \ infty} ^ {\ infty} R (\ tau) e ^ {- j \ omega \ tau} d \ tau$

• $R (\ tau) = x (\ tau) * x (- \ tau)$

Автокорреляция сигнала мощности проявляет сопряженную симметрию, т.е. $R (\ tau) = R * (- \ tau)$

Автокорреляционная функция сигнала мощности при $\ tau = 0$ (в начале координат) равна общей мощности этого сигнала. т.е.

$R (0) = \ rho$

Автокорреляционная функция сигнала мощности $\ infty {1 \ over \ tau}$,

Автокорреляционная функция сигнала мощности максимальна при $\ tau$ = 0, т.е.

$ | R (\ тау) | \ leq R (0) \, \ forall \, \ tau $

Автокорреляционная функция и спектральные плотности мощности являются парами преобразования Фурье. т.е.

$FT [R (\ tau)] = s (\ omega)$

$s (\ omega) = \ int _ {- \ infty} ^ {\ infty} R (\ tau) e ^ {- j \ omega \ tau} d \ tau$

$R (\ tau) = x (\ tau) * x (- \ tau)$

Плотность спектра

Давайте посмотрим спектры плотности:

Спектр плотности энергии

Спектр плотности энергии можно рассчитать по формуле:

E= int infty− infty|x(f)|2df $$E = \ int _ {- \ infty} ^ {\ infty} | \, x (f) \, | ^ 2 df$$

Спектр плотности мощности

Спектр плотности мощности можно рассчитать по формуле:

P= Sigma inftyn=− infty|Cn|2 $$P = \ Sigma_ {n = - \ infty} ^ {\ infty} \, | \, C_n | ^ 2$$

Функция взаимной корреляции

Кросс-корреляция — это мера сходства двух разных сигналов.

Рассмотрим два сигнала x ₁ (t) и x ₂ (t). Кросс-корреляция этих двух сигналов $R_ {12} (\ tau)$ определяется как

R12( tau)= int infty− inftyx1(t)x2(t− tau)dt quad quad text[+veshift] $$R_ {12} (\ tau) = \ int _ {- \ infty} ^ {\ infty} x_1 (t) x_2 (t- \ tau) \, dt \ quad \ quad \ text {[+ ve shift]}$$

 quad quad= int infty− inftyx1(t+ tau)x2(t)dt quad quad text[−veshift] $$\ quad \ quad = \ int _ {- \ infty} ^ {\ infty} x_1 (t + \ tau) x_2 (t) \, dt \ quad \ quad \ text {[- ve shift]}$$

Если сигналы являются сложными, то

R12( tau)= int infty− inftyx1(t)x∗2(t− tau)dt quad quad text[+veshift] $$R_ {12} (\ tau) = \ int _ {- \ infty} ^ {\ infty} x_1 (t) x_2 ^ {*} (t- \ tau) \, dt \ quad \ quad \ text {[+ ve shift]}$$

$$ \ quad \ quad = \ int _ {- \ infty} ^ {\ infty} x_1 (t + \ tau) x_2 ^ {*} (t) \, dt \ quad \ quad \ text {[- ve shift]} $ $

R21( tau)= int infty− inftyx2(t)x∗1(t− tau)dt quad quad text[+veshift] $$R_ {21} (\ tau) = \ int _ {- \ infty} ^ {\ infty} x_2 (t) x_1 ^ {*} (t- \ tau) \, dt \ quad \ quad \ text {[+ ve shift]}$$

$$ \ quad \ quad = \ int _ {- \ infty} ^ {\ infty} x_2 (t + \ tau) x_1 ^ {*} (t) \, dt \ quad \ quad \ text {[- ve shift]} $ $

Свойства кросс-корреляционной функции сигналов энергии и мощности

• Автокорреляция демонстрирует сопряженную симметрию, т.е. $R_ {12} (\ tau) = R ^ * _ {21} (- \ tau)$.

• Кросс-корреляция не коммутативна, как свертка, т.е.

  $$R_ {12} (\ tau) \ neq R_ {21} (- \ tau)$$

• Если R ₁₂ (0) = 0 означает, что если $\ int _ {- \ infty} ^ {\ infty} x_1 (t) x_2 ^ * (t) dt = 0$, то эти два сигнала называются ортогональными.

  Для сигнала питания, если  limT to infty1 overT intT over2−T over2x(t)x∗(t)dt$\ lim_ {T \ to \ infty} {1 \ over T} \ int _ {{- T \ over 2}} ^ {{T \ over 2}} \, x (t) x ^ * ( t) \, dt$, тогда два сигнала называются ортогональными.

• Функция взаимной корреляции соответствует умножению спектров одного сигнала на комплексное сопряжение спектра другого сигнала. т.е.

  $$R_ {12} (\ tau) \ leftarrow \ rightarrow X_1 (\ omega) X_2 ^ * (\ omega)$$

  Это также называется корреляционной теоремой.

Автокорреляция демонстрирует сопряженную симметрию, т.е. $R_ {12} (\ tau) = R ^ * _ {21} (- \ tau)$.

Кросс-корреляция не коммутативна, как свертка, т.е.

$$R_ {12} (\ tau) \ neq R_ {21} (- \ tau)$$

Если R ₁₂ (0) = 0 означает, что если $\ int _ {- \ infty} ^ {\ infty} x_1 (t) x_2 ^ * (t) dt = 0$, то эти два сигнала называются ортогональными.

Для сигнала питания, если  limT to infty1 overT intT over2−T over2x(t)x∗(t)dt$\ lim_ {T \ to \ infty} {1 \ over T} \ int _ {{- T \ over 2}} ^ {{T \ over 2}} \, x (t) x ^ * ( t) \, dt$, тогда два сигнала называются ортогональными.

Функция взаимной корреляции соответствует умножению спектров одного сигнала на комплексное сопряжение спектра другого сигнала. т.е.

$$R_ {12} (\ tau) \ leftarrow \ rightarrow X_1 (\ omega) X_2 ^ * (\ omega)$$

Это также называется корреляционной теоремой.

Теорема Парсеваля

Теорема Парсеваля для энергетических сигналов гласит, что полная энергия в сигнале может быть получена из спектра сигнала как

$E = {1 \ over 2 \ pi} \ int _ {- \ infty} ^ {\ infty} | X (\ omega) | ^ 2 d \ omega$

Примечание. Если сигнал имеет энергию E, то масштабированная по времени версия этого сигнала x (at) имеет энергию E / a.