Сигналы подразделяются на следующие категории:
-
Непрерывное время и сигналы дискретного времени
-
Детерминированные и недетерминированные сигналы
-
Четные и нечетные сигналы
-
Периодические и апериодические сигналы
-
Сигналы энергии и мощности
-
Реальные и мнимые сигналы
Непрерывное время и сигналы дискретного времени
Детерминированные и недетерминированные сигналы
Четные и нечетные сигналы
Периодические и апериодические сигналы
Сигналы энергии и мощности
Реальные и мнимые сигналы
Непрерывное время и сигналы дискретного времени
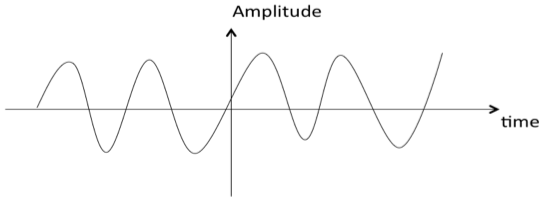
Сигнал называется непрерывным, когда он определен для всех моментов времени.
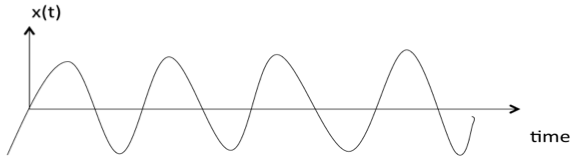
Сигнал называется дискретным, если он определен только в дискретные моменты времени /
Детерминированные и недетерминированные сигналы
Сигнал называется детерминированным, если нет неопределенности относительно его значения в любой момент времени. Или сигналы, которые могут быть точно определены математической формулой, называются детерминированными сигналами.
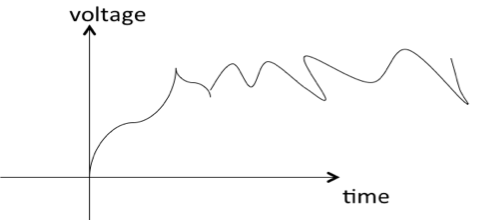
Сигнал считается недетерминированным, если в какой-то момент времени существует неопределенность относительно его значения. Недетерминированные сигналы носят случайный характер, поэтому их называют случайными сигналами. Случайные сигналы не могут быть описаны математическим уравнением. Они смоделированы в вероятностных терминах.
Четные и нечетные сигналы
Сигнал называется четным, даже если он удовлетворяет условию x (t) = x (-t)
Пример 1: t2, t4… стоимость и т. Д.
Пусть x (t) = t2
x (-t) = (-t) 2 = t2 = x (t)
следовательно, t2 является четной функцией
Пусть x (t) = t2
x (-t) = (-t) 2 = t2 = x (t)
следовательно, t2 является четной функцией
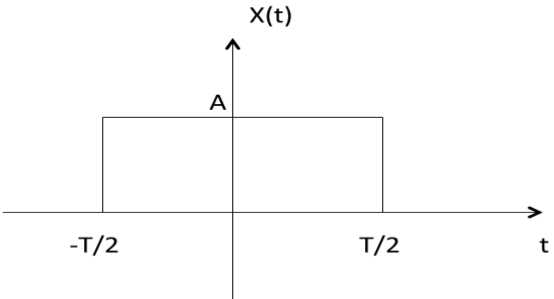
Пример 2: Как показано на следующей диаграмме, функция прямоугольника x (t) = x (-t), поэтому она также является четной функцией.
Сигнал называется нечетным, когда он удовлетворяет условию x (t) = -x (-t)
Пример: т, т3 … и грех т
Пусть х (т) = грех т
x (-t) = sin (-t) = -sin t = -x (t)
следовательно, sin t — нечетная функция.
Пусть х (т) = грех т
x (-t) = sin (-t) = -sin t = -x (t)
следовательно, sin t — нечетная функция.
Любая функция ƒ (t) может быть выражена как сумма ее четной функции ƒ e (t) и нечетной функции ƒ o (t).
ƒ ( t ) = ƒ e ( t ) + ƒ 0 ( t )
где
ƒ e ( t ) = ½ [ƒ ( t ) + ƒ ( -t )]
ƒ ( t ) = ƒ e ( t ) + ƒ 0 ( t )
где
ƒ e ( t ) = ½ [ƒ ( t ) + ƒ ( -t )]
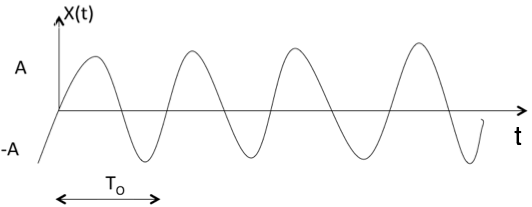
Периодические и апериодические сигналы
Сигнал называется периодическим, если он удовлетворяет условию x (t) = x (t + T) или x (n) = x (n + N).
куда
T = основной период времени,
1 / T = f = основная частота.
T = основной период времени,
1 / T = f = основная частота.
Вышеуказанный сигнал будет повторяться для каждого временного интервала T 0, следовательно, он является периодическим с периодом T 0 .
Сигналы энергии и мощности
Сигнал называется энергетическим сигналом, когда он имеет конечную энергию.
textEnergyE= int infty− inftyx2(t)dt
Сигнал называется сигналом мощности, когда он имеет конечную мощность.
textPowerP= limT to infty1 over2T intT−Tx2(t)dt
ПРИМЕЧАНИЕ. Сигнал не может быть одновременно и энергией, и мощностью одновременно. Кроме того, сигнал может не быть ни энергией, ни сигналом мощности.
Мощность энергетического сигнала = 0
Энергия силового сигнала = ∞
Мощность энергетического сигнала = 0
Энергия силового сигнала = ∞
Реальные и мнимые сигналы
Сигнал называется реальным, когда он удовлетворяет условию x (t) = x * (t)
Сигнал называется нечетным, когда он удовлетворяет условию x (t) = -x * (t)
Пример:
Если x (t) = 3, то x * (t) = 3 * = 3 здесь x (t) — реальный сигнал.
Если x (t) = 3j, то x * (t) = 3j * = -3j = -x (t), следовательно, x (t) является нечетным сигналом.
Если x (t) = 3, то x * (t) = 3 * = 3 здесь x (t) — реальный сигнал.
Если x (t) = 3j, то x * (t) = 3j * = -3j = -x (t), следовательно, x (t) является нечетным сигналом.
Примечание: для реального сигнала мнимая часть должна быть нулевой. Аналогично для воображаемого сигнала действительная часть должна быть равна нулю.