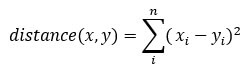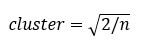В этом уроке вы узнаете
Что такое кластерный анализ?
Кластерный анализ является частью обучения без присмотра . Кластер — это группа данных, которые имеют схожие характеристики. Можно сказать, что кластерный анализ — это скорее открытие, а не предсказание. Машина ищет сходство в данных. Например, вы можете использовать кластерный анализ для следующего приложения:
- Сегментация клиентов: поиск сходства между группами клиентов
- Кластеризация фондового рынка: групповые акции по показателям
- Уменьшите размерность набора данных, сгруппировав наблюдения с одинаковыми значениями
Кластерный анализ не слишком сложен для реализации и является значимым, а также действенным для бизнеса.
Самое поразительное различие между обучением под наблюдением и без присмотра заключается в результатах. Неконтролируемое обучение создает новую переменную, метку, в то время как контролируемое обучение предсказывает результат. Машина помогает практикующему в поиске маркировать данные, основываясь на тесной взаимосвязи. Аналитик должен использовать группы и давать им имена.
Давайте сделаем пример, чтобы понять концепцию кластеризации. Для простоты мы работаем в двух измерениях. У вас есть данные об общих расходах клиентов и их возрасте. Чтобы улучшить рекламу, маркетинговая команда хочет отправлять своим клиентам более адресные электронные письма.
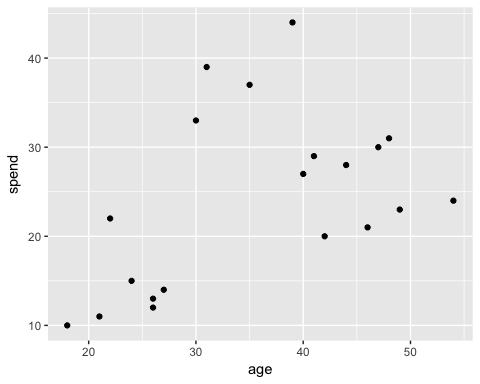
На следующем графике вы изображаете общие расходы и возраст клиентов.
library(ggplot2)
df <- data.frame(age = c(18, 21, 22, 24, 26, 26, 27, 30, 31, 35, 39, 40, 41, 42, 44, 46, 47, 48, 49, 54),
spend = c(10, 11, 22, 15, 12, 13, 14, 33, 39, 37, 44, 27, 29, 20, 28, 21, 30, 31, 23, 24)
)
ggplot(df, aes(x = age, y = spend)) +
geom_point()
В этой точке видна картина
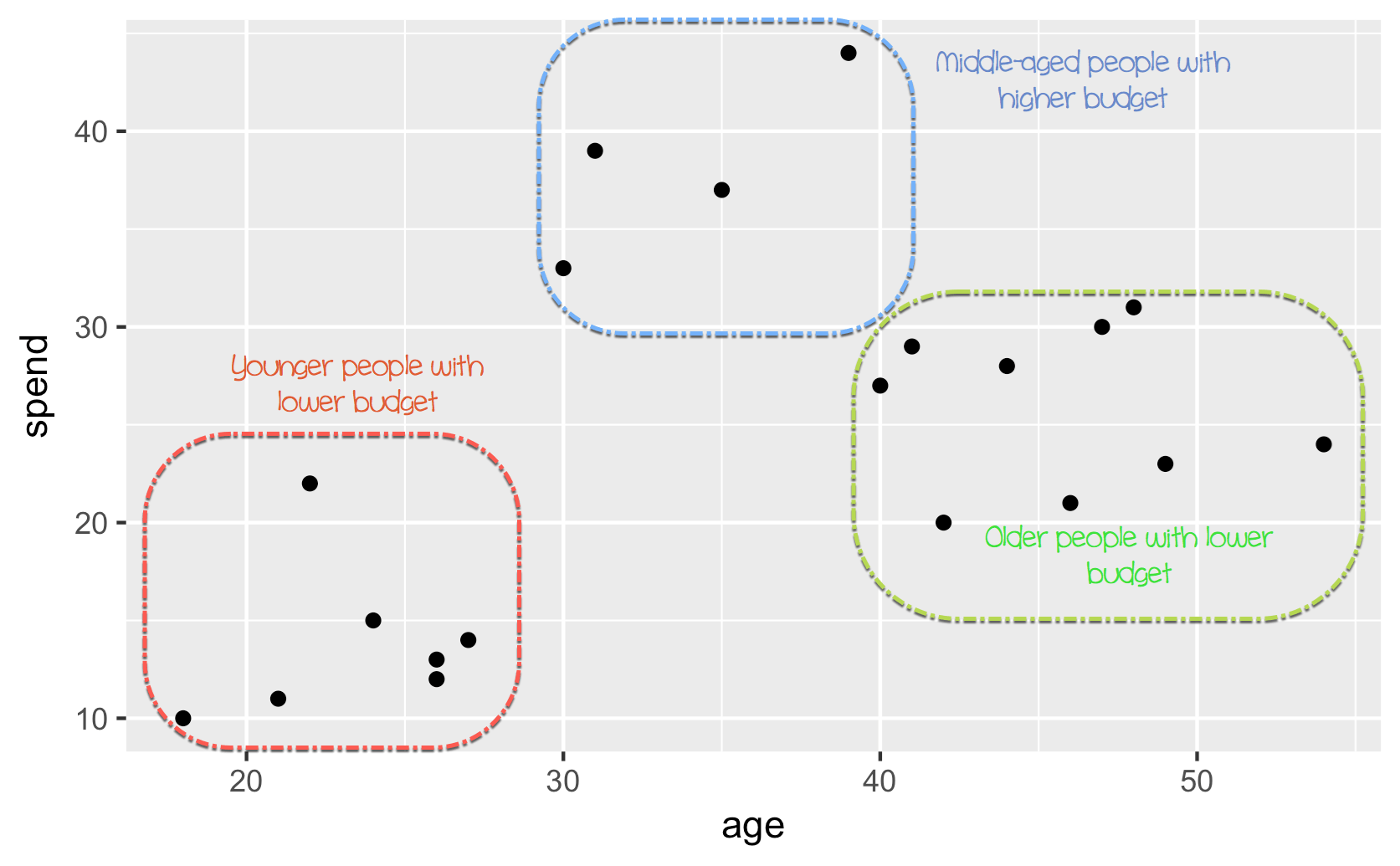
- Внизу слева вы можете увидеть молодых людей с более низкой покупательной способностью
- Верхний средний отражает людей с работой, которую они могут позволить себе тратить больше
- Наконец, пожилые люди с меньшим бюджетом.
На рисунке выше вы группируете наблюдения вручную и определяете каждую из трех групп. Этот пример несколько прост и очень нагляден. Если к набору данных добавляются новые наблюдения, вы можете пометить их в кругах. Вы определяете круг на основе нашего суждения. Вместо этого вы можете использовать машинное обучение для объективной группировки данных.
В этом уроке вы узнаете, как использовать алгоритм k-средних .
Алгоритм K-средних
K-mean is, without doubt, the most popular clustering method. Researchers released the algorithm decades ago, and lots of improvements have been done to k-means.
The algorithm tries to find groups by minimizing the distance between the observations, called local optimal solutions. The distances are measured based on the coordinates of the observations. For instance, in a two-dimensional space, the coordinates are simple and .
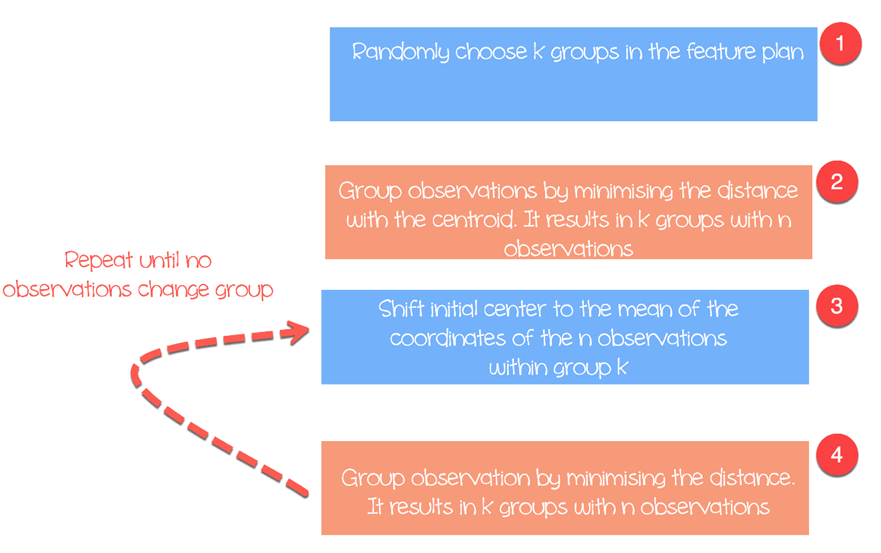
The algorithm works as follow:
- Step 1: Choose groups in the feature plan randomly
- Step 2: Minimize the distance between the cluster center and the different observations (centroid). It results in groups with observations
- Step 3: Shift the initial centroid to the mean of the coordinates within a group.
- Step 4: Minimize the distance according to the new centroids. New boundaries are created. Thus, observations will move from one group to another
- Repeat until no observation changes groups
K-means usually takes the Euclidean distance between the feature and feature :
Different measures are available such as the Manhattan distance or Minlowski distance. Note that, K-mean returns different groups each time you run the algorithm. Recall that the first initial guesses are random and compute the distances until the algorithm reaches a homogeneity within groups. That is, k-mean is very sensitive to the first choice, and unless the number of observations and groups are small, it is almost impossible to get the same clustering.
Select the number of clusters
Another difficulty found with k-mean is the choice of the number of clusters. You can set a high value of , i.e. a large number of groups, to improve stability but you might end up with overfit of data. Overfitting means the performance of the model decreases substantially for new coming data. The machine learnt the little details of the data set and struggle to generalize the overall pattern.
The number of clusters depends on the nature of the data set, the industry, business and so on. However, there is a rule of thumb to select the appropriate number of clusters:
with equals to the number of observation in the dataset.
Generally speaking, it is interesting to spend times to search for the best value of to fit with the business need.
Мы будем использовать набор данных «Цены на персональные компьютеры» для проведения нашего кластерного анализа. Этот набор данных содержит 6259 наблюдений и 10 функций. Набор данных наблюдает цену с 1993 по 1995 год 486 персональных компьютеров в США. Переменными являются цена, скорость, оперативная память, экран, CD среди других.
Вы будете действовать следующим образом:
- Импорт данных
- Тренируй модель
- Оценить модель
Импорт данных
K означает, что не подходит для факторных переменных, потому что он основан на расстоянии, а дискретные значения не возвращают значимых значений. Вы можете удалить три категориальные переменные в нашем наборе данных. Кроме того, в этом наборе данных отсутствуют пропущенные значения.
library(dplyr) PATH <-"https://raw.githubusercontent.com/guru99-edu/R-Programming/master/computers.csv" df <- read.csv(PATH) %>% select(-c(X, cd, multi, premium)) glimpse(df)
Вывод
## Observations: 6, 259 ## Variables: 7 ## $ price < int > 1499, 1795, 1595, 1849, 3295, 3695, 1720, 1995, 2225, 2... ##$ speed < int > 25, 33, 25, 25, 33, 66, 25, 50, 50, 50, 33, 66, 50, 25, ... ##$ hd < int > 80, 85, 170, 170, 340, 340, 170, 85, 210, 210, 170, 210... ##$ ram < int > 4, 2, 4, 8, 16, 16, 4, 2, 8, 4, 8, 8, 4, 8, 8, 4, 2, 4, ... ##$ screen < int > 14, 14, 15, 14, 14, 14, 14, 14, 14, 15, 15, 14, 14, 14, ... ##$ ads < int > 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, ... ## $ trend <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1...
Из сводной статистики видно, что данные имеют большие значения. Хорошей практикой расчета k средних и расстояний является изменение масштаба данных таким образом, чтобы среднее значение было равно единице, а стандартное отклонение равно нулю.
summary(df)
Вывод:
## price speed hd ram ## Min. : 949 Min. : 25.00 Min. : 80.0 Min. : 2.000 ## 1st Qu.:1794 1st Qu.: 33.00 1st Qu.: 214.0 1st Qu.: 4.000 ` ## Median :2144 Median : 50.00 Median : 340.0 Median : 8.000 ## Mean :2220 Mean : 52.01 Mean : 416.6 Mean : 8.287 ## 3rd Qu.:2595 3rd Qu.: 66.00 3rd Qu.: 528.0 3rd Qu.: 8.000 ## Max. :5399 Max. :100.00 Max. :2100.0 Max. :32.000 ## screen ads trend ## Min. :14.00 Min. : 39.0 Min. : 1.00 ## 1st Qu.:14.00 1st Qu.:162.5 1st Qu.:10.00 ## Median :14.00 Median :246.0 Median :16.00 ## Mean :14.61 Mean :221.3 Mean :15.93 ## 3rd Qu.:15.00 3rd Qu.:275.0 3rd Qu.:21.50 ## Max. :17.00 Max. :339.0 Max. :35.00
Вы перемасштабируете переменные с помощью функции scale () библиотеки dplyr. Преобразование уменьшает влияние выбросов и позволяет сравнить единственное наблюдение со средним. Если стандартизированное значение (или z-оценка ) является высоким, вы можете быть уверены, что это наблюдение действительно выше среднего (большой z-показатель означает, что эта точка далека от среднего значения в терминах стандартного отклонения. A z- оценка «два» указывает на то, что значение равно стандартному отклонению на 2 от среднего значения.
rescale_df <- df % > %
mutate(price_scal = scale(price),
hd_scal = scale(hd),
ram_scal = scale(ram),
screen_scal = scale(screen),
ads_scal = scale(ads),
trend_scal = scale(trend)) % > %
select(-c(price, speed, hd, ram, screen, ads, trend))
База R имеет функцию для запуска алгоритма k средних. Основная функция k означает:
kmeans(df, k) arguments: -df: dataset used to run the algorithm -k: Number of clusters
Тренируй модель
На третьем рисунке вы подробно рассказали, как работает алгоритм. Вы можете увидеть каждый шаг в графическом виде с помощью великолепного пакета, созданного Yi Hui (также создателем Knit для Rmarkdown). Анимация пакета недоступна в библиотеке conda. Вы можете использовать другой способ установки пакета с помощью install.packages («анимация»). Вы можете проверить, установлен ли пакет в нашей папке Anaconda.
install.packages("animation")
После загрузки библиотеки, вы добавляете .ani после kmeans, и R подготовит все шаги. Для наглядности алгоритм запускается только с измененными переменными hd и ram с тремя кластерами.
set.seed(2345) library(animation) kmeans.ani(rescale_df[2:3], 3)
Код Объяснение
- kmeans.ani (rescale_df [2: 3], 3): выберите столбцы 2 и 3 набора данных rescale_df и запустите алгоритм с k наборами, равными 3. Постройте анимацию.
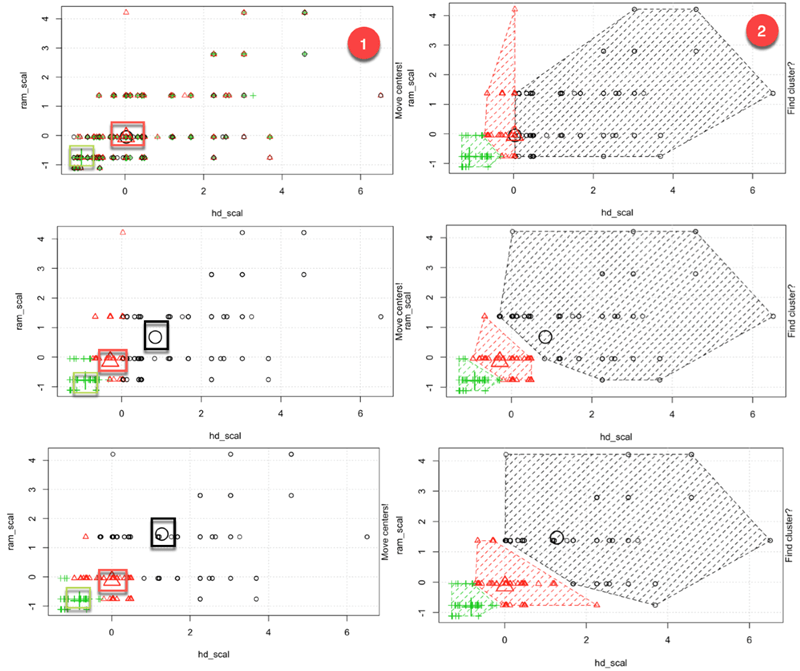
Вы можете интерпретировать анимацию следующим образом:
- Шаг 1: R случайным образом выбирает три очка
- Шаг 2: Вычислите евклидово расстояние и нарисуйте кластеры. У вас есть один кластер зеленого цвета внизу слева, один большой кластер цвета черного цвета справа и красный между ними.
- Шаг 3: Вычислить центроид, то есть среднее значение кластеров
- Повторяйте до тех пор, пока кластер данных не изменится
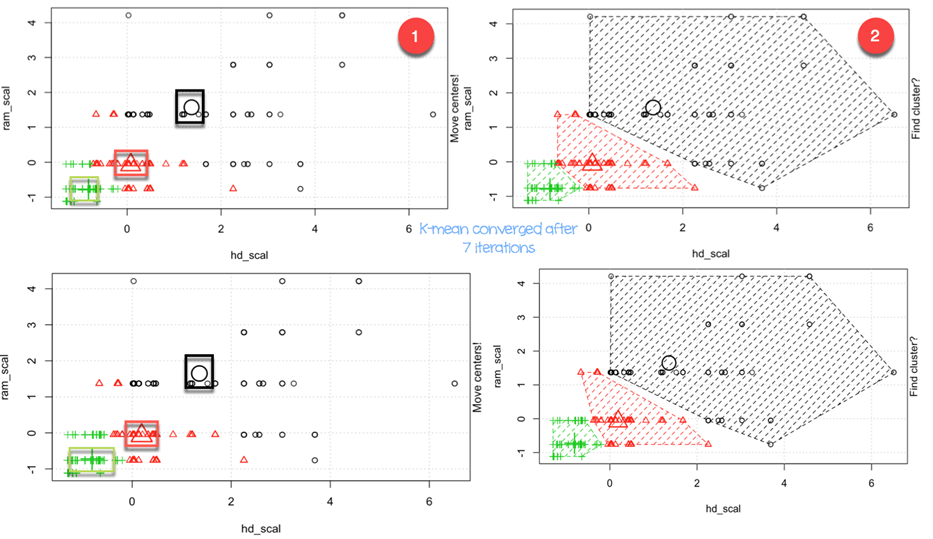
Алгоритм сходился после семи итераций. Вы можете запустить алгоритм k-mean в нашем наборе данных с пятью кластерами и назвать его pc_cluster.
pc_cluster <-kmeans(rescale_df, 5)
- Список pc_cluster содержит семь интересных элементов:
- pc_cluster $ cluster: указывает кластер каждого наблюдения
- pc_cluster $ центров: кластерные центры
- pc_cluster $ totss: общая сумма квадратов
- pc_cluster $ insidess: в пределах суммы квадрата. Количество возвращаемых компонентов равно `k`
- pc_cluster $ tot.withinss: сумма внутренних
- pc_clusterbetweenss: общая сумма квадратов минус в пределах суммы квадратов
- pc_cluster $ size: количество наблюдений в каждом кластере
Вы будете использовать сумму в пределах суммы квадратов (т.е. tot.withinss), чтобы вычислить оптимальное количество кластеров k. Нахождение k действительно является существенной задачей.
Оптимальный к
Один из методов выбора лучшего k называется методом локтя . Этот метод использует внутригрупповую однородность или внутригрупповую неоднородность для оценки изменчивости. Другими словами, вас интересует процент дисперсии, объясняемой каждым кластером. Можно ожидать, что изменчивость будет увеличиваться с увеличением количества кластеров, или же гетерогенность уменьшается. Наша задача — найти значение k, которое выходит за пределы убывающей доходности. Добавление нового кластера не улучшает изменчивость данных, поскольку для объяснения остается очень мало информации.
В этом уроке мы находим эту точку, используя меру неоднородности. Общая сумма квадратов в кластерах — это значение tot.withinss в списке, возвращаемое функцией kmean ().
Вы можете построить график колен и найти оптимальное k следующим образом:
- Шаг 1: Построить функцию для вычисления общей суммы квадратов в кластерах
- Шаг 2: Запустите алгоритм раз
- Шаг 3: Создать фрейм данных с результатами алгоритма
- Шаг 4: График результатов
Шаг 1) Построить функцию для вычисления суммы квадратов в кластерах
Вы создаете функцию, которая запускает алгоритм k-mean и сохраняете сумму в кластерах сумму квадратов
kmean_withinss <- function(k) {
cluster <- kmeans(rescale_df, k)
return (cluster$tot.withinss)
}
Код Объяснение
- function (k): установить количество аргументов в функции
- kmeans (rescale_df, k): запустить алгоритм k раз
- return (cluster $ tot.withinss): сохранить общую сумму квадратов в кластерах.
Вы можете проверить функцию с равными 2.
Вывод:
## Try with 2 cluster
kmean_withinss(2)
Вывод:
## [1] 27087.07
Шаг 2) Запустите алгоритм n раз
Вы будете использовать функцию sapply () для запуска алгоритма в диапазоне k. Этот метод быстрее, чем создание цикла и сохранение значения.
# Set maximum cluster max_k <-20 # Run algorithm over a range of k wss <- sapply(2:max_k, kmean_withinss)
Код Объяснение
- max_k <-20: установить максимальное количество до 20
- sapply (2: max_k, kmean_withinss): запустить функцию kmean_withinss () в диапазоне 2: max_k, то есть от 2 до 20.
Шаг 3) Создайте фрейм данных с результатами алгоритма
После создания и тестирования нашей функции вы можете запустить алгоритм k-mean в диапазоне от 2 до 20, сохранить значения tot.withinss.
# Create a data frame to plot the graph elbow <-data.frame(2:max_k, wss)
Код Объяснение
- data.frame (2: max_k, wss): создать фрейм данных с выводом хранилища алгоритма в wss.
Шаг 4) График результатов
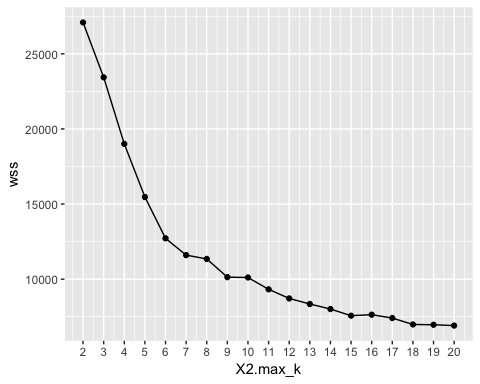
Вы строите график, чтобы визуализировать, где находится точка локтя
# Plot the graph with gglop
ggplot(elbow, aes(x = X2.max_k, y = wss)) +
geom_point() +
geom_line() +
scale_x_continuous(breaks = seq(1, 20, by = 1))
Из графика видно, что оптимальное k равно семи, где кривая начинает давать убывающую доходность.
Получив оптимальное k, вы перезапустите алгоритм с k, равным 7, и оцените кластеры.
Изучение кластера
pc_cluster_2 <-kmeans(rescale_df, 7)
Как упоминалось ранее, вы можете получить доступ к оставшейся интересной информации в списке, возвращаемом функцией kmean ().
pc_cluster_2$cluster pc_cluster_2$centers pc_cluster_2$size
Оценочная часть носит субъективный характер и опирается на использование алгоритма. Наша цель — собрать компьютер с похожими функциями. Компьютерный парень может выполнять работу вручную и группировать компьютер на основе своего опыта. Однако этот процесс займет много времени и будет подвержен ошибкам. Алгоритм среднего значения может подготовить поле для него, предложив кластеры.
В качестве предварительной оценки вы можете проверить размер кластеров.
pc_cluster_2$size
Вывод:
## [1] 608 1596 1231 580 1003 699 542
Первый кластер состоит из 608 наблюдений, в то время как самый маленький кластер, номер 4, имеет только 580 компьютеров. Было бы хорошо иметь однородность между кластерами, если нет, то может потребоваться более тонкая подготовка данных.
Вы получаете более глубокий взгляд на данные с центральным компонентом. Строки ссылаются на нумерацию кластера и столбцы переменных, используемых алгоритмом. Значения представляют собой среднюю оценку по каждому кластеру для интересующего столбца. Стандартизация облегчает интерпретацию. Положительные значения указывают, что z-показатель для данного кластера выше общего среднего значения. Например, кластер 2 имеет самую высокую среднюю цену среди всех кластеров.
center <-pc_cluster_2$centers center
Вывод:
## price_scal hd_scal ram_scal screen_scal ads_scal trend_scal ## 1 -0.6372457 -0.7097995 -0.691520682 -0.4401632 0.6780366 -0.3379751 ## 2 -0.1323863 0.6299541 0.004786730 2.6419582 -0.8894946 1.2673184 ## 3 0.8745816 0.2574164 0.513105797 -0.2003237 0.6734261 -0.3300536 ## 4 1.0912296 -0.2401936 0.006526723 2.6419582 0.4704301 -0.4132057 ## 5 -0.8155183 0.2814882 -0.307621003 -0.3205176 -0.9052979 1.2177279 ## 6 0.8830191 2.1019454 2.168706085 0.4492922 -0.9035248 1.2069855 ## 7 0.2215678 -0.7132577 -0.318050275 -0.3878782 -1.3206229 -1.5490909
Вы можете создать тепловую карту с помощью ggplot, чтобы помочь нам выделить разницу между категориями.
Цвета по умолчанию для ggplot необходимо изменить с помощью библиотеки RColorBrewer. Вы можете использовать библиотеку conda и код для запуска в терминале:
Конда установить -cr r-rcolorbrewer
Чтобы создать тепловую карту, необходимо выполнить три шага:
- Постройте фрейм данных со значениями центра и создайте переменную с номером кластера
- Измените данные с помощью функции collect () библиотеки tidyr. Вы хотите преобразовать данные из широкого в длинный.
- Создайте палитру цветов с помощью функции colorRampPalette ()
Шаг 1) Создайте фрейм данных
Давайте создадим измененный набор данных
library(tidyr) # create dataset with the cluster number cluster <- c(1: 7) center_df <- data.frame(cluster, center) # Reshape the data center_reshape <- gather(center_df, features, values, price_scal: trend_scal) head(center_reshape)
Вывод:
## cluster features values ## 1 1 price_scal -0.6372457 ## 2 2 price_scal -0.1323863 ## 3 3 price_scal 0.8745816 ## 4 4 price_scal 1.0912296 ## 5 5 price_scal -0.8155183 ## 6 6 price_scal 0.8830191
Шаг 2) Измените данные
Код ниже создает палитру цветов, которую вы будете использовать для построения тепловой карты.
library(RColorBrewer) # Create the palette hm.palette <-colorRampPalette(rev(brewer.pal(10, 'RdYlGn')),space='Lab')
Шаг 3) Визуализация
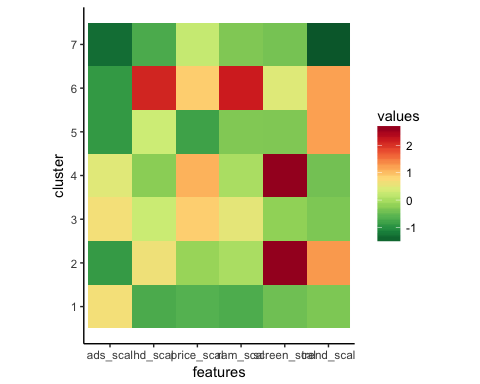
Вы можете построить график и посмотреть, как выглядят кластеры.
# Plot the heat map
ggplot(data = center_reshape, aes(x = features, y = cluster, fill = values)) +
scale_y_continuous(breaks = seq(1, 7, by = 1)) +
geom_tile() +
coord_equal() +
scale_fill_gradientn(colours = hm.palette(90)) +
theme_classic()
Резюме
Мы можем обобщить алгоритм k-среднего в таблице ниже
|
пакет |
Задача |
функция |
аргумент |
|---|---|---|---|
|
база |
Поезд к-среднее |
kmeans () |
дф, к |
|
Кластер доступа |
kmeans () $ кластера |
||
|
Кластерные центры |
kmeans () $ центров |
||
|
Размер кластера |
kmeans () $ размер |