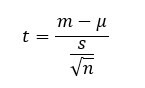Что такое статистический вывод?
Статистический вывод — это искусство генерирования выводов о распределении данных. Специалист по данным часто подвергается сомнению, на которое можно ответить только с научной точки зрения. Таким образом, статистический вывод — это стратегия проверки правильности гипотезы, то есть подтверждения данными.
Общая стратегия оценки гипотезы заключается в проведении t-теста. С помощью t-критерия можно определить, имеют ли две группы одинаковое среднее значение. T-тест также называется тестом для студентов . Т-тест может быть оценен для:
- Один вектор (т. Е. Один образец t-критерия)
- Два вектора из одной группы образцов (т. Е. Парный t-критерий).
Вы предполагаете, что оба вектора выбраны случайным образом, независимы и происходят из нормально распределенной популяции с неизвестными, но равными отклонениями.
В этом уроке вы узнаете
Что такое t-тест?
Основная идея t-критерия — использовать статистику для оценки двух противоположных гипотез:
- H0: NULL гипотеза: среднее значение совпадает с использованной выборкой
- H3: истинная гипотеза: среднее значение отличается от используемого образца
T-критерий обычно используется для небольших выборок. Чтобы выполнить t-тест, вы должны предположить нормальность данных.
Основной синтаксис для t.test ():
t.test(x, y = NULL,
mu = 0, var.equal = FALSE)
arguments:
- x : A vector to compute the one-sample t-test
- y: A second vector to compute the two sample t-test
- mu: Mean of the population- var.equal: Specify if the variance of the two vectors are equal. By default, set to `FALSE`
T-тест с одним образцом
T-критерий, или критерий Стьюдента, сравнивает среднее значение вектора с теоретическим средним значением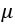 
. Формула, используемая для вычисления t-критерия:
Вот
относится к среднему- к теоретическому среднему
- s стандартное отклонение
- по количеству наблюдений.
Чтобы оценить статистическую значимость t-критерия, вам необходимо вычислить значение p . Значение p варьируется от 0 до 1 и интерпретируется следующим образом:
- Значение p ниже 0,05 означает, что вы абсолютно уверены в том, что отвергли нулевую гипотезу, поэтому H3 принимается.
- Значение р выше 0,05 указывает на то, что у вас недостаточно доказательств, чтобы отвергнуть нулевую гипотезу.
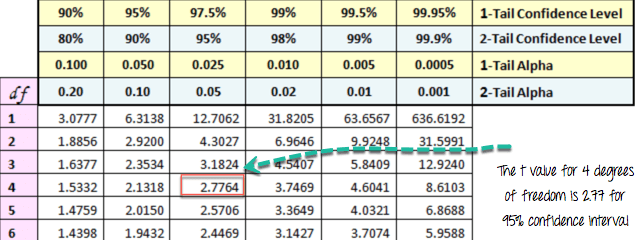
Вы можете построить pvalue, посмотрев на соответствующее абсолютное значение t-критерия в распределении Стьюдента со степенями свободы, равными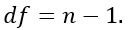 
Например, если у вас есть 5 наблюдений, вам нужно сравнить наше t-значение с t-значением в распределении Стьюдента с 4 степенями свободы и 95-процентным доверительным интервалом. Чтобы отклонить нулевую гипотезу, значение t должно быть выше, чем 2,77.
Таблица ниже:
Пример:
Предположим, вы — компания, производящая печенье. Каждое печенье должно содержать 10 грамм сахара. Печенье производится на машине, которая добавляет сахар в миску, прежде чем все перемешать. Вы считаете, что машина не добавляет 10 г сахара на каждое печенье. Если ваше предположение верно, машина должна быть исправлена. Вы сохранили уровень сахара в тридцать печенья.
Примечание. Вы можете создать случайный вектор с помощью функции rnorm (). Эта функция генерирует нормально распределенные значения. Основной синтаксис:
rnorm(n, mean, sd) arguments - n: Number of observations to generate - mean: The mean of the distribution. Optional - sd: The standard deviation of the distribution. Optional
Вы можете создать распределение с 30 наблюдениями со средним значением 9,99 и стандартным отклонением 0,04.
set.seed(123) sugar_cookie <- rnorm(30, mean = 9.99, sd = 0.04) head(sugar_cookie)
Вывод:
## [1] 9.967581 9.980793 10.052348 9.992820 9.995172 10.058603
Вы можете использовать t-тест для одного образца, чтобы проверить, отличается ли уровень сахара от рецепта. Вы можете нарисовать тест гипотезы:
- H0: средний уровень сахара равен 10
- H3: средний уровень сахара отличается от 10
Вы используете уровень значимости 0,05.
# H0 : mu = 10 t.test(sugar_cookie, mu = 10)
Вот вывод
Значение р в одном образце t-критерия составляет 0,1079 и выше 0,05. Вы можете быть уверены на 95%, что количество сахара, добавляемое машиной, составляет от 9,973 до 10,002 грамма. Вы не можете отвергнуть нулевую (H0) гипотезу. Недостаточно доказательств того, что количество сахара, добавляемое машиной, не соответствует рецепту.
Парный t-тест
Парный t-критерий или зависимый образец t-критерия используется, когда среднее значение для обработанной группы вычисляется дважды. Основное применение парного t-теста:
- A / B тестирование: сравнить два варианта
- Контрольные исследования: до / после лечения
Пример:
Компания по производству напитков заинтересована в том, чтобы узнать, как действует программа скидок на распродажи. Компания решила следить за ежедневными продажами одного из своих магазинов, где продвигается программа. В конце программы компания хочет узнать, есть ли статистическая разница между средними продажами магазина до и после программы.
- Компания отслеживала продажи каждый день до начала программы. Это наш первый вектор.
- Программа продвигается на одну неделю, а продажи регистрируются каждый день. Это наш второй вектор.
- Вы проведете t-тест, чтобы оценить эффективность программы. Это называется парным t-тестом, поскольку значения обоих векторов поступают из одного и того же распределения (т. Е. Из одного магазина).
Проверка гипотезы это:
- H0: нет разницы в среднем
- H3: два средства разные
Помните, одно предположение в t-тесте — неизвестная, но равная дисперсия. В действительности данные едва имеют одинаковое среднее значение, и это приводит к неверным результатам для t-теста.
Одним из решений для ослабления предположения о равной дисперсии является использование теста Уэлча. R предполагает, что две дисперсии не равны по умолчанию. В вашем наборе данных оба вектора имеют одинаковую дисперсию, вы можете установить var.equal = TRUE.
Вы создаете два случайных вектора из гауссовского распределения с более высоким средним для продаж после программы.
set.seed(123) # sales before the program sales_before <- rnorm(7, mean = 50000, sd = 50) # sales after the program.This has higher mean sales_after <- rnorm(7, mean = 50075, sd = 50) # draw the distribution t.test(sales_before, sales_after,var.equal = TRUE)
You obtained a p-value of 0.04606, lower than the threshold of 0.05. You conclude the averages of the two groups are significantly different. The program improves the sales of shops.
Summary
The t-test belongs to the family of inferential statistics. It is commonly employed to find out if there is a statistical difference between the means of two groups.
We can summarize the t-test is the table below:
|
test |
Hypothesis to test |
p-value |
code |
optional argument |
|---|---|---|---|---|
|
one-sample t-test |
Mean of a vector is different from the theoretical mean |
0.05 |
t.test(x, mu = mean) |
|
|
paired sample t-test |
Mean A is different from mean B for the same group |
0.06 |
t.test(A,B, mu = mean) |
var.equal= TRUE |
If we assume the variances are equal, we need to change the parameter var.equal= TRUE.