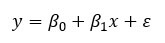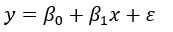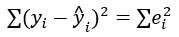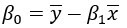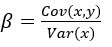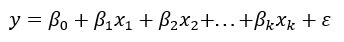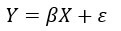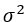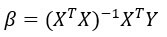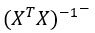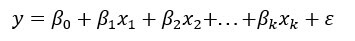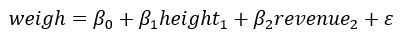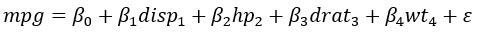Учебники

27) Ступенчатая регрессия в R

Март 18, 2020

В этом уроке вы узнаете

Простая линейная регрессия

Линейная регрессия отвечает на простой вопрос: можете ли вы измерить точную связь между одной целевой переменной и набором предикторов?

Простейшей из вероятностных моделей является модель прямой линии:

где

  • y = зависимая переменная
  • x = независимая переменная
  • = случайная ошибка компонента
  • = перехват
  • = Коэффициент х

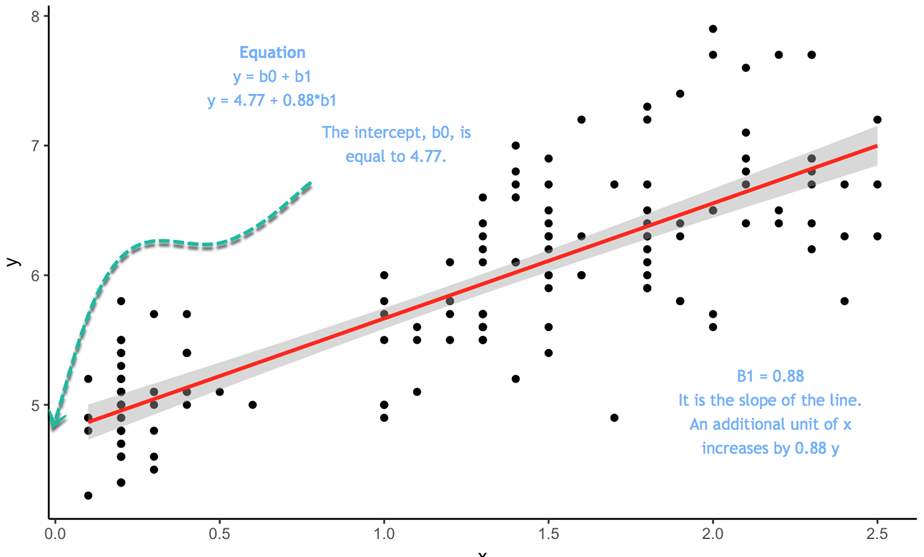
Рассмотрим следующий сюжет:

Уравнение есть 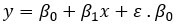перехват. Если x равно 0, y будет равно пересечению 4.77. это наклон линии. Он говорит, в какой пропорции у меняется, когда х меняется.

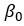
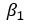
Чтобы оценить оптимальные значения и , вы используете метод, называемый Обыкновенные наименьшие квадраты (OLS) . Этот метод пытается найти параметры, которые минимизируют сумму квадратов ошибок, то есть вертикальное расстояние между прогнозируемыми значениями y и фактическими значениями y. Разница известна как термин ошибки .

Прежде чем оценивать модель, вы можете определить, является ли линейная зависимость между y и x вероятной, построив график рассеяния.

разброс точек

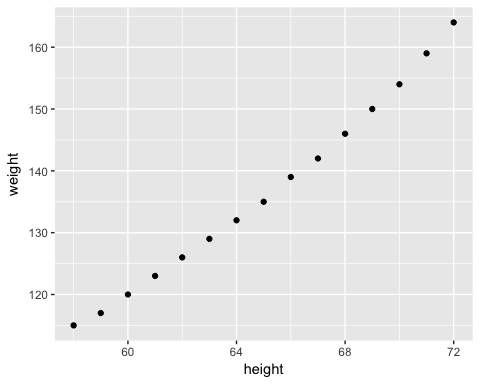
Мы будем использовать очень простой набор данных для объяснения концепции простой линейной регрессии. Мы импортируем средние высоты и веса для американских женщин. Набор данных содержит 15 наблюдений. Вы хотите измерить, положительно ли соотносятся высоты с весами.

library(ggplot2)
path <- 'https://raw.githubusercontent.com/guru99-edu/R-Programming/master/women.csv'
df <-read.csv(path)
ggplot(df,aes(x=height, y =  weight))+
geom_point()

Вывод:

Диаграмма рассеяния предполагает общую тенденцию к увеличению y при увеличении x. На следующем шаге вы будете измерять, сколько увеличивается для каждого дополнительного.

Наименьшие квадраты Оценки

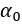
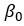
В простой регрессии OLS вычисление и является простым. Цель не в том, чтобы показать происхождение в этом уроке. Вы будете только писать формулу.

Вы хотите оценить:

Целью регрессии OLS является минимизация следующего уравнения:

где

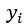
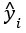
является фактическим значением и является прогнозируемым значением.

Решение для IS

Обратите внимание, что 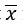означает среднее значение х

Решение для IS

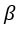
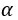
В R вы можете использовать функции cov () и var () для оценки, и вы можете использовать функцию mean () для оценки 

beta <- cov(df$height, df$weight) / var (df$height)
beta

Вывод: 

##[1] 3.45
alpha <- mean(df$weight) - beta * mean(df$height)
alpha

Вывод: 

## [1] -87.51667

Коэффициент бета подразумевает, что для каждого дополнительного роста вес увеличивается на 3,45.

Оценка простого линейного уравнения вручную не идеальна. R предоставляет подходящую функцию для оценки этих параметров. Вы увидите эту функцию в ближайшее время. Перед этим мы расскажем, как вручную вычислить простую модель линейной регрессии. На пути к исследованию данных вы просто или никогда не сможете оценить простую линейную модель. В большинстве случаев регрессионные задачи выполняются по множеству оценок.

Множественная линейная регрессия

Более практические применения регрессионного анализа используют модели, которые являются более сложными, чем простая прямолинейная модель. Вероятностная модель, которая включает в себя более одной независимой переменной, называется моделью множественной регрессии . Общая форма этой модели:

В матричной записи вы можете переписать модель:

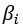
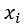
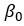
Зависимая переменная y теперь является функцией от k независимых переменных. Значение коэффициента определяет вклад независимой переменной и .

Мы кратко представим сделанное нами предположение о случайной ошибке 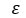OLS:

  • Среднее значение равно 0
  • Дисперсия равна
  • Нормальное распределение
  • Случайные ошибки независимы (в вероятностном смысле)

Вам необходимо найти 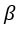вектор коэффициентов регрессии, которые минимизируют сумму квадратов ошибок между прогнозируемыми и фактическими значениями y.

Решение в закрытой форме:

с:

  • указывает на транспонирование матрицы X
  • указывает на обратимую матрицу

Мы используем набор данных mtcars. Вы уже знакомы с набором данных. Наша цель — предсказать милю на галлон по ряду функций.

Непрерывные переменные

На данный момент вы будете использовать только непрерывные переменные и оставить в стороне категориальные особенности. Переменная am является двоичной переменной, принимающей значение 1, если коробка передач механическая, и 0 для автоматических автомобилей; vs также является двоичной переменной.

library(dplyr)
df <- mtcars % > %
select(-c(am, vs, cyl, gear, carb))
glimpse(df)

Вывод: 

## Observations: 32
## Variables: 6
## $ mpg  <dbl> 21.0, 21.0, 22.8, 21.4, 18.7, 18.1, 14.3, 24.4, 22.8, 19....
## $ disp <dbl> 160.0, 160.0, 108.0, 258.0, 360.0, 225.0, 360.0, 146.7, 1...
## $ hp   <dbl> 110, 110, 93, 110, 175, 105, 245, 62, 95, 123, 123, 180, ...
## $ drat <dbl> 3.90, 3.90, 3.85, 3.08, 3.15, 2.76, 3.21, 3.69, 3.92, 3.9...
## $ wt   <dbl> 2.620, 2.875, 2.320, 3.215, 3.440, 3.460, 3.570, 3.190, 3...
## $ qsec <dbl> 16.46, 17.02, 18.61, 19.44, 17.02, 20.22, 15.84, 20.00, 2...

Вы можете использовать функцию lm () для вычисления параметров. Основной синтаксис этой функции:

lm(formula, data, subset)
Arguments:
	-formula: The equation you want to estimate	
	-data: The dataset used
	-subset: Estimate the model on a subset of the dataset

Помните, что уравнение имеет следующую форму

в R

  • Символ = заменяется на ~
  • Каждый х заменяется именем переменной
  • Если вы хотите удалить константу, добавьте -1 в конце формулы

Пример:

Вы хотите оценить вес людей на основе их роста и доходов. Уравнение

Уравнение в R записывается следующим образом:

y ~ X1 + X2 + … + Xn # с перехватом

Итак, для нашего примера:

  • Взвесьте ~ рост + доход

Ваша цель — оценить милю на галлон на основе набора переменных. Уравнение для оценки:

Вы оцените свою первую линейную регрессию и сохраните результат в подходящем объекте.

model <- mpg~.disp + hp + drat + wt
fit <- lm(model, df)
fit

Код Объяснение

  • модель <- mpg ~ . disp + hp + drat + wt: сохранить модель для оценки
  • lm (модель, df): оценка модели с помощью фрейма данных df
## 
## Call:
## lm(formula = model, data = df)
## 
## Coefficients:
## (Intercept)         disp           hp         drat           wt  
##    16.53357      0.00872     -0.02060      2.01577     -4.38546  
##        qsec  
##     0.64015

Вывод не дает достаточно информации о качестве посадки. Вы можете получить доступ к более подробной информации, такой как значимость коэффициентов, степень свободы и форма остатков, с помощью функции summary ().

summary(fit)

Вывод: 

## return the p-value and coefficient
## 
## Call:
## lm(formula = model, data = df)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.5404 -1.6701 -0.4264  1.1320  5.4996 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)   
## (Intercept) 16.53357   10.96423   1.508  0.14362   
## disp         0.00872    0.01119   0.779  0.44281   
## hp          -0.02060    0.01528  -1.348  0.18936   
## drat         2.01578    1.30946   1.539  0.13579   
## wt          -4.38546    1.24343  -3.527  0.00158 **
## qsec         0.64015    0.45934   1.394  0.17523   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.558 on 26 degrees of freedom
## Multiple R-squared:  0.8489, Adjusted R-squared:  0.8199 
## F-statistic: 29.22 on 5 and 26 DF, p-value: 6.892e-10

Вывод из вышеприведенного вывода таблицы

  • Приведенная выше таблица доказывает, что существует сильная отрицательная связь между массой и пробегом и положительная связь с drat.
  • Только переменная wt оказывает статистическое влияние на миль на галлон. Помните, что для проверки гипотезы в статистике мы используем:
    • H0: нет статистического воздействия
    • H3: предиктор оказывает существенное влияние на у
    • Если значение р ниже 0,05, это означает, что переменная является статистически значимой
  • Скорректированный R-квадрат: Разница объясняется моделью. В вашей модели модель объясняет 82 процента дисперсии y. R в квадрате всегда между 0 и 1. Чем выше, тем лучше

Вы можете запустить тест ANOVA, чтобы оценить влияние каждого объекта на отклонения с помощью функции anova (). 

anova(fit)

Вывод: 

## Analysis of Variance Table
## 
## Response: mpg
##           Df Sum Sq Mean Sq  F value   Pr(>F)    
## disp       1 808.89  808.89 123.6185 2.23e-11 ***
## hp         1  33.67   33.67   5.1449 0.031854 *  
## drat       1  30.15   30.15   4.6073 0.041340 *  
## wt         1  70.51   70.51  10.7754 0.002933 ** 
## qsec       1  12.71   12.71   1.9422 0.175233    
## Residuals 26 170.13    6.54                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

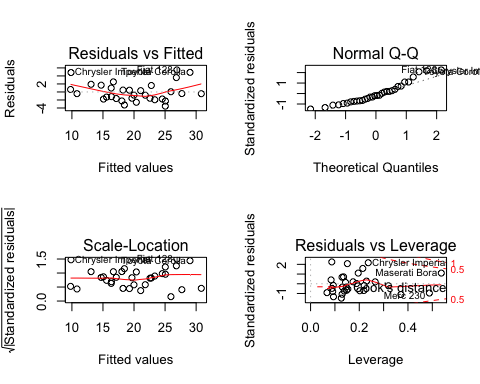
Более традиционный способ оценки производительности модели состоит в отображении остатка в зависимости от различных показателей.

Вы можете использовать функцию plot () для отображения четырех графиков:

— остатки против установленных значений

— Нормальный график QQ: теоретический квартиль против стандартизированных остатков

— Scale-Location: установленные значения в сравнении с квадратными корнями стандартизированных остатков.

— Остатки против плеча: плечо против стандартизированных остатков

Вы добавляете код par (mfrow = c (2,2)) перед графиком (fit). Если вы не добавите эту строку кода, R предложит вам нажать команду ввода, чтобы отобразить следующий график.

par(mfrow=(2,2))

Код Объяснение

  • (mfrow = c (2,2)): вернуть окно с четырьмя графиками рядом.
  • Первые 2 добавляют количество строк
  • Второе 2 добавляет количество столбцов.
  • Если вы напишите (mfrow = c (3,2)): вы создадите окно с 3 строками и 2 столбцами 
plot(fit)

Вывод:

Формула lm () возвращает список, содержащий много полезной информации. Вы можете получить к ним доступ с помощью созданного вами подходящего объекта, за которым следует знак $ и информация, которую вы хотите извлечь.

— коэффициенты: `соответствовать $ коэффициентам`

— остатки: `соответствуют $ остаткам`

— установленное значение: `fit $ fit.values`

Факторы регрессии

В последней оценке модели вы регрессируете mpg только для непрерывных переменных. Добавить факторные переменные в модель просто. Вы добавляете переменную am в вашу модель. Важно убедиться, что переменная является уровнем фактора, а не непрерывной.

df <- mtcars % > %
mutate(cyl = factor(cyl),
    vs = factor(vs),
    am = factor(am),
    gear = factor(gear),
    carb = factor(carb))
summary(lm(model, df))

Вывод: 

## 
## Call:
## lm(formula = model, data = df)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.5087 -1.3584 -0.0948  0.7745  4.6251 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)  
## (Intercept) 23.87913   20.06582   1.190   0.2525  
## cyl6        -2.64870    3.04089  -0.871   0.3975  
## cyl8        -0.33616    7.15954  -0.047   0.9632  
## disp         0.03555    0.03190   1.114   0.2827  
## hp          -0.07051    0.03943  -1.788   0.0939 .
## drat         1.18283    2.48348   0.476   0.6407  
## wt          -4.52978    2.53875  -1.784   0.0946 .
## qsec         0.36784    0.93540   0.393   0.6997  
## vs1          1.93085    2.87126   0.672   0.5115  
## am1          1.21212    3.21355   0.377   0.7113  
## gear4        1.11435    3.79952   0.293   0.7733  
## gear5        2.52840    3.73636   0.677   0.5089  
## carb2       -0.97935    2.31797  -0.423   0.6787  
## carb3        2.99964    4.29355   0.699   0.4955  
## carb4        1.09142    4.44962   0.245   0.8096  
## carb6        4.47757    6.38406   0.701   0.4938  
## carb8        7.25041    8.36057   0.867   0.3995  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.833 on 15 degrees of freedom
## Multiple R-squared:  0.8931, Adjusted R-squared:  0.779 
## F-statistic:  7.83 on 16 and 15 DF,  p-value: 0.000124

R использует первый уровень фактора в качестве базовой группы. Вам необходимо сравнить коэффициенты другой группы с базовой группой.

Пошаговая регрессия

Последняя часть этого урока посвящена алгоритму пошаговой регрессии . Целью этого алгоритма является добавление и удаление потенциальных кандидатов в моделях и сохранение тех, кто оказывает существенное влияние на зависимую переменную. Этот алгоритм имеет смысл, когда набор данных содержит большой список предикторов. Вам не нужно вручную добавлять и удалять независимые переменные. Построена ступенчатая регрессия для выбора лучших кандидатов, подходящих для модели.

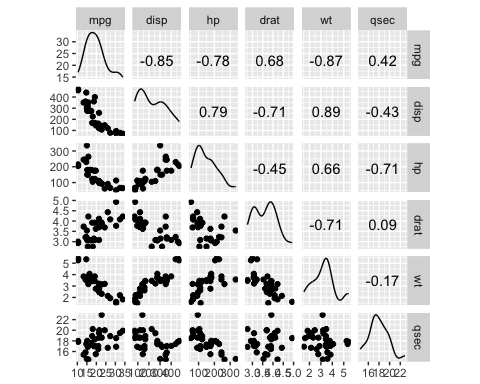
Давайте посмотрим в действии, как это работает. Вы используете набор данных mtcars с непрерывными переменными только для педагогической иллюстрации. Прежде чем приступить к анализу, полезно установить различия между данными с помощью корреляционной матрицы. Библиотека GGally является расширением ggplot2.

Библиотека включает в себя различные функции для отображения сводной статистики, такой как корреляция и распределение всех переменных в матрице. Мы будем использовать функцию ggscatmat, но вы можете обратиться к виньетке для получения дополнительной информации о библиотеке GGally.

Основной синтаксис для ggscatmat (): 

ggscatmat(df, columns = 1:ncol(df), corMethod = "pearson")
arguments:
-df:  A matrix of continuous variables
-columns: Pick up the columns to use in the function. By default, all columns are used
-corMethod: Define the function to compute the correlation between variable. By default, the algorithm uses the Pearson formula

Вы отображаете корреляцию для всех ваших переменных и решаете, какой из них будет лучшим кандидатом для первого шага ступенчатой ​​регрессии. Есть некоторые сильные корреляции между вашими переменными и зависимой переменной, mpg.

library(GGally)
df <- mtcars % > %
	select(-c(am, vs, cyl, gear, carb))
ggscatmat(df, columns = 1: ncol(df))

Вывод:

Пошаговая регрессия

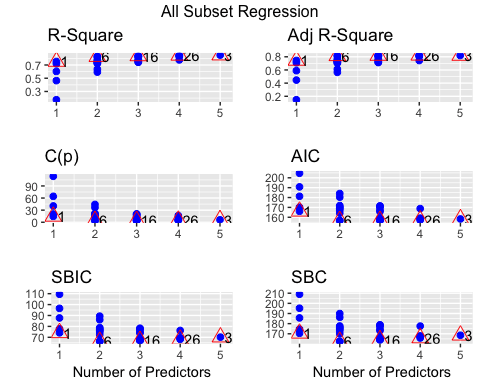
Выбор переменных является важной частью для подгонки модели. Пошаговая регрессия выполнит процесс поиска автоматически. Чтобы оценить, сколько возможных вариантов есть в наборе данных, вы вычисляете 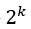с помощью k количество предсказателей. Количество возможностей растет с увеличением числа независимых переменных. Вот почему вам нужно иметь автоматический поиск.

Вам необходимо установить пакет olsrr из CRAN. В Анаконде пакет пока недоступен. Следовательно, вы устанавливаете его прямо из командной строки:

install.packages("olsrr")

Вы можете построить все подмножества возможностей с помощью критериев соответствия (т. Е. R-квадрат, Скорректированный R-квадрат, Байесовский критерий). Модель с самыми низкими критериями AIC будет окончательной моделью.

library(olsrr)
model <- mpg~.
fit <- lm(model, df)
test <- ols_all_subset(fit)
plot(test)

Код Объяснение

  • mpg ~ .: построить модель для оценки
  • lm (модель, df): запустить модель OLS
  • ols_all_subset (fit): построить графики с соответствующей статистической информацией
  • сюжет (тест): построение графиков

Вывод:

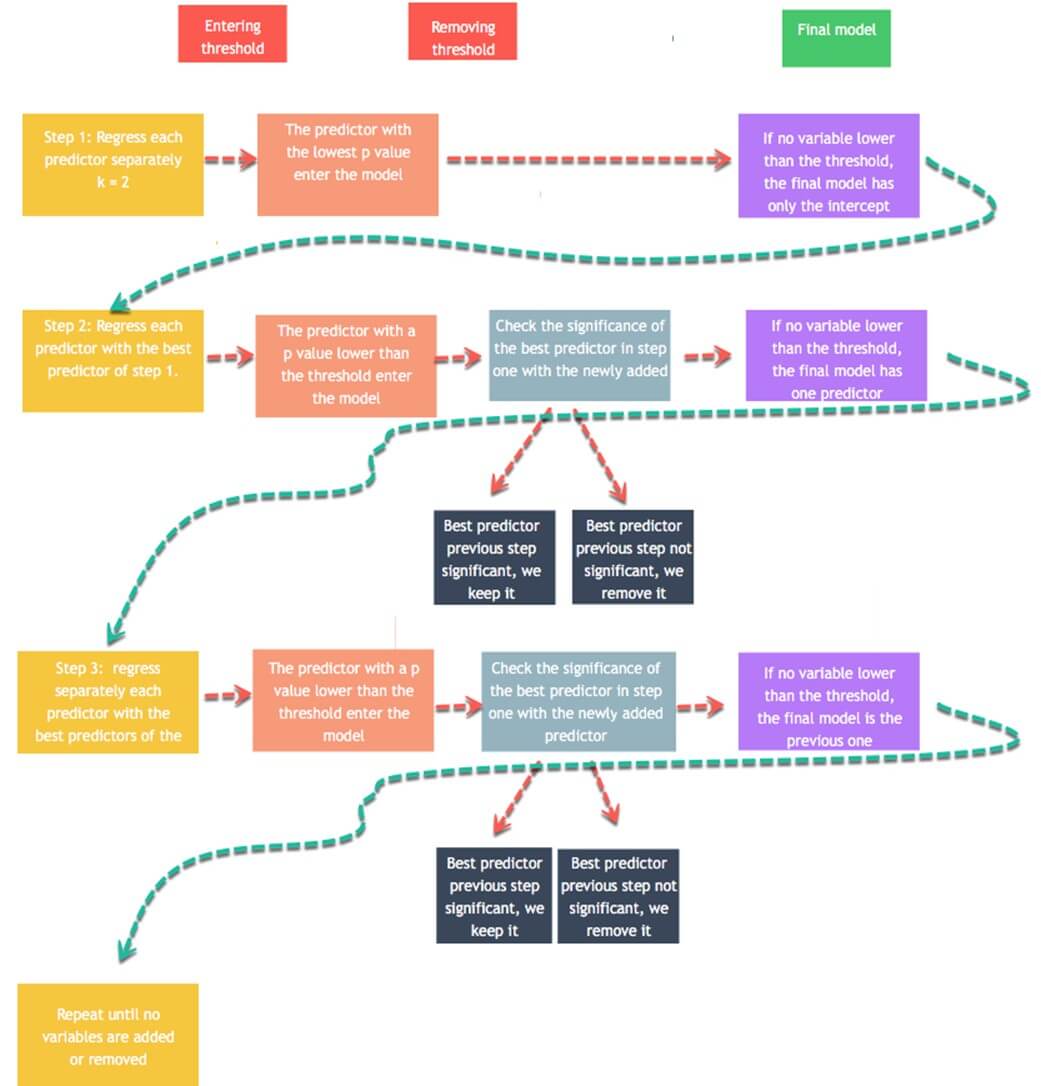
Модели линейной регрессии используют t-критерий для оценки статистического влияния независимой переменной на зависимую переменную. Исследователи устанавливают максимальный порог в 10 процентов, при этом более низкие значения указывают на более сильную статистическую связь. Стратегия ступенчатой ​​регрессии строится вокруг этого теста, чтобы добавлять и удалять потенциальных кандидатов. Алгоритм работает следующим образом:

  • Шаг 1: Регресс каждого предиктора по y отдельно. А именно, регрессировать x_1 на y, x_2 на y на x_n. Сохраните значение p и оставьте для регрессора значение p ниже определенного порогового значения (по умолчанию 0,1). Предикторы со значением ниже порогового значения будут добавлены в окончательную модель. Если ни одна переменная не имеет p-значения ниже порога входа, то алгоритм останавливается, и ваша окончательная модель имеет только константу.
  • Шаг 2: Используйте предиктор с самым низким значением p и добавьте отдельно одну переменную. Вы регрессируете константу, лучший предиктор первого и третьего шага. Вы добавляете в пошаговую модель новые предикторы со значением ниже порога ввода. Если ни одна переменная не имеет значения p ниже 0,1, тогда алгоритм останавливается, и ваша окончательная модель имеет только один предиктор. Вы регрессируете пошаговую модель, чтобы проверить значимость лучших предикторов шага 1. Если он выше порога удаления, вы сохраняете его в пошаговой модели. В противном случае вы исключаете это.
  • Шаг 3: Вы повторяете шаг 2 на новой лучшей пошаговой модели. Алгоритм добавляет предикторы в пошаговую модель на основе введенных значений и исключает предиктор из пошаговой модели, если он не удовлетворяет порогу исключения.
  • Алгоритм продолжается до тех пор, пока ни одна переменная не может быть добавлена ​​или исключена.

Вы можете выполнить алгоритм с помощью функции ols_stepwise () из пакета olsrr. 

ols_stepwise(fit, pent = 0.1, prem = 0.3, details = FALSE)

arguments:
-fit:  Model to fit. Need to use `lm()`before to run `ols_stepwise()
-pent: Threshold of the p-value used to enter a variable into the stepwise model. By default, 0.1
-prem: Threshold of the p-value used to exclude a variable into the stepwise model. By default, 0.3
-details: Print the details of each step

Перед этим мы покажем вам шаги алгоритма. Ниже приведена таблица с зависимыми и независимыми переменными:

Зависимая переменная

Независимые переменные

миль на галлон

Индик.точки

л.с.

провались ты

вес

qsec

Начните

Начнем с того, что алгоритм начинается с запуска модели по каждой независимой переменной отдельно. В таблице приведены значения p для каждой модели.

## [[1]]
##  (Intercept)         disp 
## 3.576586e-21 9.380327e-10 
## 
## [[2]]
##  (Intercept)           hp 
## 6.642736e-18 1.787835e-07 
## 
## [[3]]
##  (Intercept)         drat 
## 0.1796390847 0.0000177624 
## 
## [[4]]
##  (Intercept)           wt 
## 8.241799e-19 1.293959e-10 
## 
## [[5]
## (Intercept)        qsec 
##  0.61385436  0.01708199

Чтобы ввести модель, алгоритм сохраняет переменную с самым низким значением p. Из приведенного выше вывода, это вес

Шаг 1

На первом этапе алгоритм запускает mpg для wt и других переменных независимо. 

## [[1]]
##  (Intercept)           wt         disp
## 4.910746e-16 7.430725e-03 6.361981e-02 
## 
## [[2]]
##  (Intercept)           wt           hp 
## 2.565459e-20 1.119647e-06 1.451229e-03 
## 
## [[3]]
##  (Intercept)           wt         drat 
## 2.737824e-04 1.589075e-06 3.308544e-01 
## 
## [[4]]
##  (Intercept)           wt         qsec 
## 7.650466e-04 2.518948e-11 1.499883e-03

Каждая переменная является потенциальным кандидатом для ввода в окончательную модель. Однако алгоритм сохраняет только переменную с более низким значением p. Оказывается, hp имеет чуть меньшее значение p, чем qsec. Следовательно, hp входит в финальную модель

Шаг 2

Алгоритм повторяет первый шаг, но на этот раз с двумя независимыми переменными в окончательной модели. 

## [[1]]
##  (Intercept)           wt           hp         disp 
## 1.161936e-16 1.330991e-03 1.097103e-02 9.285070e-01 
## 
## [[2]]
##  (Intercept)           wt           hp         drat 
## 5.133678e-05 3.642961e-04 1.178415e-03 1.987554e-01 
## 
## [[3]]
##  (Intercept)           wt           hp         qsec 
## 2.784556e-03 3.217222e-06 2.441762e-01 2.546284e-01

Ни одна из переменных, которые вошли в окончательную модель, не имеет достаточно низкого значения p. Алгоритм останавливается здесь; у нас есть окончательная модель:

## 
## Call:
## lm(formula = mpg ~ wt + hp, data = df)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -3.941 -1.600 -0.182  1.050  5.854 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 37.22727    1.59879  23.285  < 2e-16 ***
## wt          -3.87783    0.63273  -6.129 1.12e-06 ***
## hp          -0.03177    0.00903  -3.519  0.00145 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.593 on 29 degrees of freedom
## Multiple R-squared:  0.8268, Adjusted R-squared:  0.8148 
## F-statistic: 69.21 on 2 and 29 DF,  p-value: 9.109e-12

Вы можете использовать функцию ols_stepwise () для сравнения результатов. 

stp_s <-ols_stepwise(fit, details=TRUE)

Вывод:

Алгоритм находит решение после 2 шагов и возвращает тот же результат, что и раньше.

В конце вы можете сказать, что модели объясняются двумя переменными и перехватом. Миля на галлон отрицательно коррелирует с полной мощностью и весом

## You are selecting variables based on p value...
## 1 variable(s) added....
## Variable Selection Procedure
##  Dependent Variable: mpg 
## 
##  Stepwise Selection: Step 1 
## 
##  Variable wt Entered 
## 
##                         Model Summary                          
## --------------------------------------------------------------
## R                       0.868       RMSE                3.046 
## R-Squared               0.753       Coef. Var          15.161 
## Adj. R-Squared          0.745       MSE                 9.277 
## Pred R-Squared          0.709       MAE                 2.341 
## --------------------------------------------------------------
##  RMSE: Root Mean Square Error 
##  MSE: Mean Square Error 
##  MAE: Mean Absolute Error 
##		ANOVA                                 
## --------------------------------------------------------------------
##                 Sum of                                              
##                Squares        DF    Mean Square      F         Sig. 
## --------------------------------------------------------------------
## Regression     847.725         1        847.725    91.375    0.0000 
## Residual       278.322        30          9.277                     
## Total         1126.047        31                                    
## --------------------------------------------------------------------
## 
##                                   Parameter Estimates                                    
## ----------------------------------------------------------------------------------------
##       model      Beta    Std. Error    Std. Beta      t        Sig      lower     upper 
## ----------------------------------------------------------------------------------------
## (Intercept)    37.285         1.878                 19.858    0.000    33.450    41.120 
##          wt    -5.344         0.559       -0.868    -9.559    0.000    -6.486    -4.203 
## ----------------------------------------------------------------------------------------
## 1 variable(s) added...
## Stepwise Selection: Step 2 
## 
##  Variable hp Entered 
## 
##                         Model Summary                          
## --------------------------------------------------------------
## R                       0.909       RMSE                2.593 
## R-Squared               0.827       Coef. Var          12.909 
## Adj. R-Squared          0.815       MSE                 6.726 
## Pred R-Squared          0.781       MAE                 1.901 
## --------------------------------------------------------------
##  RMSE: Root Mean Square Error 
##  MSE: Mean Square Error 
##  MAE: Mean Absolute Error 
##			ANOVA                                 
## --------------------------------------------------------------------
##                 Sum of                                              
##                Squares        DF    Mean Square      F         Sig. 
## --------------------------------------------------------------------
## Regression     930.999         2        465.500    69.211    0.0000 
## Residual       195.048        29          6.726                     
## Total         1126.047        31                                    
## --------------------------------------------------------------------
## 
##                                   Parameter Estimates                                    
## ----------------------------------------------------------------------------------------
##       model      Beta    Std. Error    Std. Beta      t        Sig      lower     upper 
## ----------------------------------------------------------------------------------------
## (Intercept)    37.227         1.599                 23.285    0.000    33.957    40.497 
##          wt    -3.878         0.633       -0.630    -6.129    0.000    -5.172    -2.584 
##          hp    -0.032         0.009       -0.361    -3.519    0.001    -0.050    -0.013 
## ----------------------------------------------------------------------------------------
## No more variables to be added or removed.

Machine learning

Machine learning is becoming widespread among data scientist and is deployed in hundreds of products you use daily. One of the first ML application was spam filter.

Ниже приведены другие применения машинного обучения.

  • Выявление нежелательных спам-сообщений в электронной почте
  • Сегментация поведения клиентов для целевой рекламы
  • Сокращение мошеннических операций с кредитными картами
  • Оптимизация использования энергии в доме и офисе
  • Распознавание лиц

Контролируемое обучение

В контролируемом обучении данные обучения, которые вы вводите в алгоритм, содержат метку.

Классификация , вероятно, является наиболее используемой методикой обучения под наблюдением. Одной из первых задач классификации, которой занимались исследователи, был спам-фильтр. Цель обучения состоит в том, чтобы предсказать, будет ли электронное письмо классифицировано как спам или хам (хорошее письмо). После этапа обучения машина может определить класс электронной почты.

Регрессии обычно используются в области машинного обучения для прогнозирования непрерывного значения. Задача регрессии может предсказать значение зависимой переменной на основе набора независимых переменных (также называемых предикторами или регрессорами). Например, линейные регрессии могут предсказать цену акций, прогноз погоды, продажи и так далее.

Вот список некоторых фундаментальных алгоритмов обучения под наблюдением.

  • Линейная регрессия
  • Логистическая регрессия
  • Ближайшие соседи
  • Машина опорных векторов (SVM)
  • Деревья решений и случайный лес
  • Нейронные сети

Неконтролируемое обучение

При неконтролируемом обучении данные обучения не имеют маркировки. Система пытается учиться без ссылки. Ниже приведен список неконтролируемых алгоритмов обучения.

  • K-среднее
  • Иерархический кластерный анализ
  • Максимальное ожидание
  • Визуализация и уменьшение размерности
  • Анализ главных компонентов
  • Ядро PCA
  • Локально-линейное вложение

Резюме

Обычная регрессия в наименьшем квадрате может быть обобщена в таблице ниже:

Библиотека

Задача

функция

аргументы

база

Вычислить линейную регрессию

лм ()

формула, данные

база

Обобщить модель

подводить итоги()

поместиться

база

Коэффициенты извлечения

лм () $ коэффициент

база

Извлечь остатки

ле () $ невязка

база

Извлечь установленное значение

лм () $ fitted.values

olsrr

Выполнить пошаговую регрессию

ols_stepwise ()

Fit, Pent = 0,1, Prem = 0,3, детали = FALSE

Примечание : не забудьте преобразовать категориальную переменную в фактор прежде, чем соответствовать модели.

 

114
Share: