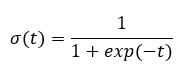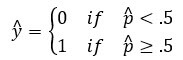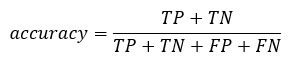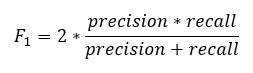Что такое логистическая регрессия?
Логистическая регрессия используется для прогнозирования класса, т. Е. Вероятности. Логистическая регрессия может точно предсказать бинарный результат.
Представьте, что вы хотите предсказать, будет ли кредит отклонен / принят на основе многих атрибутов. Логистическая регрессия имеет вид 0/1. y = 0, если кредит отклонен, y = 1, если он принят.
Модель логистической регрессии отличается от модели линейной регрессии в двух отношениях.
- Прежде всего, логистическая регрессия принимает только дихотомический (двоичный) ввод в качестве зависимой переменной (то есть вектор 0 и 1).
- Во-вторых, результат измеряется следующей вероятностной функцией связи, называемой сигмоидальной, из-за ее S-образной формы:
Выход функции всегда между 0 и 1. Проверьте изображение ниже
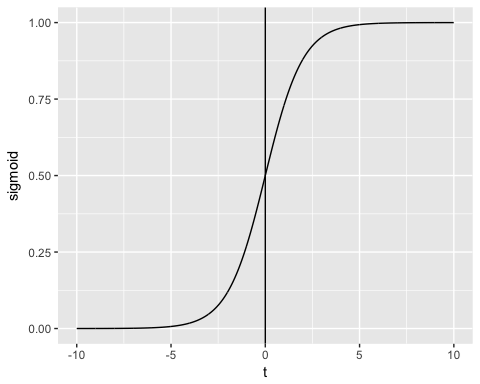
Функция сигмоида возвращает значения от 0 до 1. Для задачи классификации нам нужен дискретный вывод 0 или 1.
Чтобы преобразовать непрерывный поток в дискретное значение, мы можем установить предел решения на 0,5. Все значения выше этого порога классифицируются как 1
В этом уроке вы узнаете
- Что такое логистическая регрессия?
- Как создать обобщенную модель лайнера (GLM)
- Шаг 1) Проверьте непрерывные переменные
- Шаг 2) Проверьте факторные переменные
- Шаг 3) Разработка функций
- Шаг 4) Сводная статистика
- Шаг 5) Поезд / тестовый набор
- Шаг 6) Постройте модель
- Шаг 7) Оцените производительность модели
Как создать обобщенную модель лайнера (GLM)
Давайте использовать набор данных для взрослых, чтобы проиллюстрировать логистическую регрессию. «Adult» — отличный набор данных для задачи классификации. Цель состоит в том, чтобы предсказать, превысит ли годовой доход человека в долларах 50.000. Набор данных содержит 46 033 наблюдения и десять функций:
- возраст: возраст человека. числовой
- образование: образовательный уровень личности. Фактор.
- marital.status: семейное положение личности. Фактор, т. Е. Никогда не состоявший в браке, женатый, гражданский супруг, …
- пол: пол человека. Фактор, то есть мужчина или женщина
- доход: целевая переменная. Доход выше или ниже 50К. Фактор то есть> 50K, <= 50K
среди других
library(dplyr)
data_adult <-read.csv("https://raw.githubusercontent.com/guru99-edu/R-Programming/master/adult.csv")
glimpse(data_adult)
Вывод:
Observations: 48,842 Variables: 10 $ x <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,... $ age <int> 25, 38, 28, 44, 18, 34, 29, 63, 24, 55, 65, 36, 26... $ workclass <fctr> Private, Private, Local-gov, Private, ?, Private,... $ education <fctr> 11th, HS-grad, Assoc-acdm, Some-college, Some-col... $ educational.num <int> 7, 9, 12, 10, 10, 6, 9, 15, 10, 4, 9, 13, 9, 9, 9,... $ marital.status <fctr> Never-married, Married-civ-spouse, Married-civ-sp... $ race <fctr> Black, White, White, Black, White, White, Black, ... $ gender <fctr> Male, Male, Male, Male, Female, Male, Male, Male,... $ hours.per.week <int> 40, 50, 40, 40, 30, 30, 40, 32, 40, 10, 40, 40, 39... $ income <fctr> <=50K, <=50K, >50K, >50K, <=50K, <=50K, <=50K, >5...
Мы будем действовать следующим образом:
- Шаг 1: Проверьте непрерывные переменные
- Шаг 2: Проверьте факторные переменные
- Шаг 3: Разработка функций
- Шаг 4: Сводная статистика
- Шаг 5: Поезд / тестовый набор
- Шаг 6: Постройте модель
- Шаг 7: Оцените производительность модели
- Шаг 8: улучшить модель
Ваша задача — предсказать, у какого человека будет доход выше 50К.
В этом руководстве каждый шаг будет подробно описан для выполнения анализа реального набора данных.
Шаг 1) Проверьте непрерывные переменные
На первом этапе вы можете увидеть распределение непрерывных переменных.
continuous <-select_if(data_adult, is.numeric) summary(continuous)
Код Объяснение
- непрерывный <- select_if (data_adult, is.numeric): используйте функцию select_if () из библиотеки dplyr, чтобы выбрать только числовые столбцы
- итоговая (непрерывная): печать итоговой статистики
Вывод:
## X age educational.num hours.per.week ## Min. : 1 Min. :17.00 Min. : 1.00 Min. : 1.00 ## 1st Qu.:11509 1st Qu.:28.00 1st Qu.: 9.00 1st Qu.:40.00 ## Median :23017 Median :37.00 Median :10.00 Median :40.00 ## Mean :23017 Mean :38.56 Mean :10.13 Mean :40.95 ## 3rd Qu.:34525 3rd Qu.:47.00 3rd Qu.:13.00 3rd Qu.:45.00 ## Max. :46033 Max. :90.00 Max. :16.00 Max. :99.00
Из приведенной выше таблицы видно, что данные имеют совершенно разные масштабы, а у hours.per.weeks большие выбросы (.ie посмотрите на последний квартиль и максимальное значение).
С этим можно справиться, выполнив два шага:
- 1: подготовить график распределения hours.per.week
- 2: стандартизировать непрерывные переменные
- Сюжет о распределении
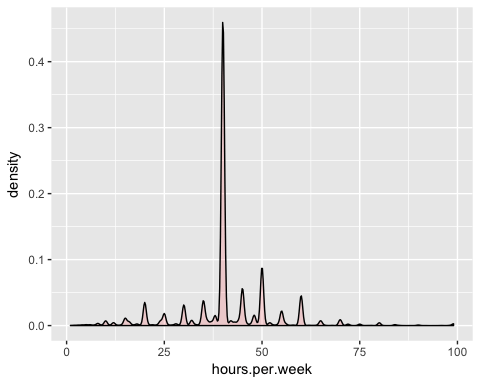
Давайте посмотрим ближе на распределение hours.per.week
# Histogram with kernel density curve
library(ggplot2)
ggplot(continuous, aes(x = hours.per.week)) +
geom_density(alpha = .2, fill = "#FF6666")
Вывод:
Переменная имеет много выбросов и нечеткое распределение. Вы можете частично решить эту проблему, удалив верхние 0,01 процента часов в неделю.
Основной синтаксис квантиля:
quantile(variable, percentile) arguments: -variable: Select the variable in the data frame to compute the percentile -percentile: Can be a single value between 0 and 1 or multiple value. If multiple, use this format: `c(A,B,C, ...) - `A`,`B`,`C` and `...` are all integer from 0 to 1.
Мы вычисляем верхний 2-процентный процентиль
top_one_percent <- quantile(data_adult$hours.per.week, .99) top_one_percent
Код Объяснение
- квантиль (data_adult $ hours.per.week, .99): вычислить значение 99 процентов рабочего времени
Вывод:
## 99% ## 80
98 процентов населения работает под 80 часов в неделю.
Вы можете сбросить наблюдения выше этого порога. Вы используете фильтр из библиотеки dplyr.
data_adult_drop <-data_adult %>% filter(hours.per.week<top_one_percent) dim(data_adult_drop)
Вывод:
## [1] 45537 10
- Стандартизируйте непрерывные переменные
Вы можете стандартизировать каждый столбец для повышения производительности, поскольку ваши данные имеют разный масштаб. Вы можете использовать функцию mutate_if из библиотеки dplyr. Основной синтаксис:
mutate_if(df, condition, funs(function)) arguments: -`df`: Data frame used to compute the function - `condition`: Statement used. Do not use parenthesis - funs(function): Return the function to apply. Do not use parenthesis for the function
Вы можете стандартизировать числовые столбцы следующим образом:
data_adult_rescale <- data_adult_drop % > % mutate_if(is.numeric, funs(as.numeric(scale(.)))) head(data_adult_rescale)
Код Объяснение
- mutate_if (is.numeric, funs (scale)): условие является только числовым столбцом, а функция — масштабной
Вывод:
## X age workclass education educational.num ## 1 -1.732680 -1.02325949 Private 11th -1.22106443 ## 2 -1.732605 -0.03969284 Private HS-grad -0.43998868 ## 3 -1.732530 -0.79628257 Local-gov Assoc-acdm 0.73162494 ## 4 -1.732455 0.41426100 Private Some-college -0.04945081 ## 5 -1.732379 -0.34232873 Private 10th -1.61160231 ## 6 -1.732304 1.85178149 Self-emp-not-inc Prof-school 1.90323857 ## marital.status race gender hours.per.week income ## 1 Never-married Black Male -0.03995944 <=50K ## 2 Married-civ-spouse White Male 0.86863037 <=50K ## 3 Married-civ-spouse White Male -0.03995944 >50K ## 4 Married-civ-spouse Black Male -0.03995944 >50K ## 5 Never-married White Male -0.94854924 <=50K ## 6 Married-civ-spouse White Male -0.76683128 >50K
Шаг 2) Проверьте факторные переменные
Этот шаг имеет две цели:
- Проверьте уровень в каждом категориальном столбце
- Определите новые уровни
Мы разделим этот шаг на три части:
- Выберите категориальные столбцы
- Сохраните гистограмму каждого столбца в списке
- Распечатать графики
Мы можем выбрать столбцы коэффициентов с помощью кода ниже:
# Select categorical column factor <- data.frame(select_if(data_adult_rescale, is.factor)) ncol(factor)
Код Объяснение
- data.frame (select_if (data_adult, is.factor)): мы сохраняем факторные столбцы в факторе в типе фрейма данных. Библиотека ggplot2 требует объект фрейма данных.
Вывод:
## [1] 6
Набор данных содержит 6 категориальных переменных
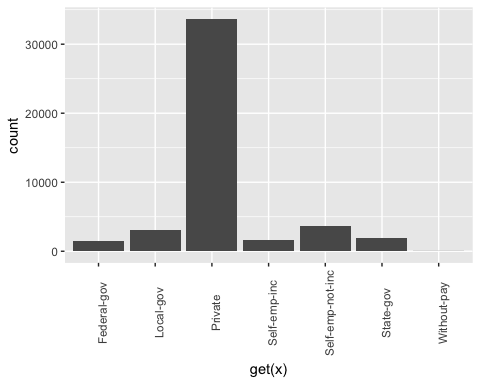
Второй шаг является более квалифицированным. Вы хотите построить гистограмму для каждого столбца в факторе фрейма данных. Автоматизировать процесс удобнее, особенно в ситуациях, когда имеется много столбцов.
library(ggplot2)
# Create graph for each column
graph <- lapply(names(factor),
function(x)
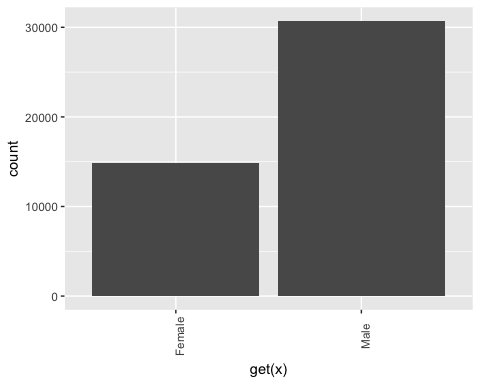
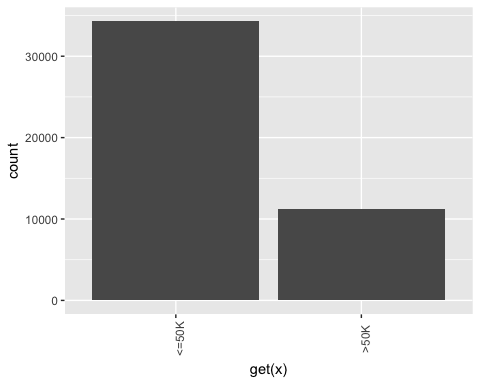
ggplot(factor, aes(get(x))) +
geom_bar() +
theme(axis.text.x = element_text(angle = 90)))
Код Объяснение
- lapply (): используйте функцию lapply (), чтобы передать функцию во все столбцы набора данных. Вы сохраняете вывод в списке
- функция (х): функция будет обрабатываться для каждого х. Здесь х столбцы
- ggplot (factor, aes (get (x))) + geom_bar () + theme (axis.text.x = element_text (angle = 90)): создайте гистограмму для каждого элемента x. Обратите внимание, чтобы вернуть x в виде столбца, вам нужно включить его в get ()
Последний шаг относительно прост. Вы хотите напечатать 6 графиков.
# Print the graph graph
Вывод:
## [[1]]
## ## [[2]]
## ## [[3]]
## ## [[4]]
## ## [[5]]
## ## [[6]]
Примечание. Используйте следующую кнопку для перехода к следующему графику.
Шаг 3) Разработка функций
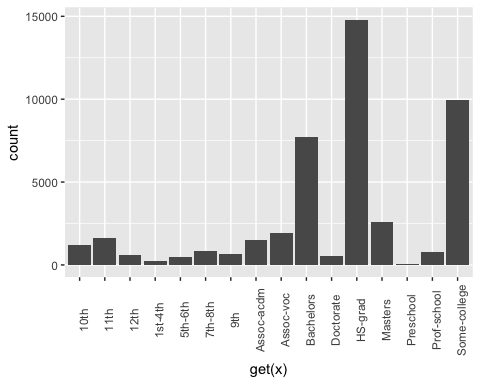
Переучить образование
Из приведенного выше графика видно, что переменное образование имеет 16 уровней. Это существенно, и некоторые уровни имеют относительно небольшое количество наблюдений. Если вы хотите улучшить объем информации, которую вы можете получить из этой переменной, вы можете преобразовать ее в более высокий уровень. А именно, вы создаете большие группы с одинаковым уровнем образования. Например, низкий уровень образования будет преобразован в отсев. Высшие уровни образования будут изменены на магистерские.
Вот деталь:
|
Старый уровень |
Новый уровень |
|---|---|
|
дошкольный |
выбывать |
|
десятые |
Выбывать |
|
11 |
Выбывать |
|
12 |
Выбывать |
|
Первый-четвёртый |
Выбывать |
|
Пятые-шестые |
Выбывать |
|
Седьмой-восьмой |
Выбывать |
|
девятую |
Выбывать |
|
HS-Град |
HighGrad |
|
Несколько колледжей некоторые колледжи |
сообщество |
|
Assoc-ACDM |
сообщество |
|
Assoc-VOC |
сообщество |
|
Бакалавры |
Бакалавры |
|
Мастера |
Мастера |
|
Проф-школа |
Мастера |
|
докторская степень |
кандидат наук |
recast_data <- data_adult_rescale % > %
select(-X) % > %
mutate(education = factor(ifelse(education == "Preschool" | education == "10th" | education == "11th" | education == "12th" | education == "1st-4th" | education == "5th-6th" | education == "7th-8th" | education == "9th", "dropout", ifelse(education == "HS-grad", "HighGrad", ifelse(education == "Some-college" | education == "Assoc-acdm" | education == "Assoc-voc", "Community",
ifelse(education == "Bachelors", "Bachelors",
ifelse(education == "Masters" | education == "Prof-school", "Master", "PhD")))))))
Код Объяснение
- Мы используем глагол mutate из библиотеки dplyr. Мы меняем ценности образования с заявлением ifelse
В таблице ниже вы создаете сводную статистику, чтобы увидеть, в среднем, сколько лет обучения (z-значение) требуется, чтобы достичь степени бакалавра, магистра или доктора наук.
recast_data % > % group_by(education) % > % summarize(average_educ_year = mean(educational.num), count = n()) % > % arrange(average_educ_year)
Вывод:
## # A tibble: 6 x 3 ## education average_educ_year count ## <fctr> <dbl> <int> ## 1 dropout -1.76147258 5712 ## 2 HighGrad -0.43998868 14803 ## 3 Community 0.09561361 13407 ## 4 Bachelors 1.12216282 7720 ## 5 Master 1.60337381 3338 ## 6 PhD 2.29377644 557
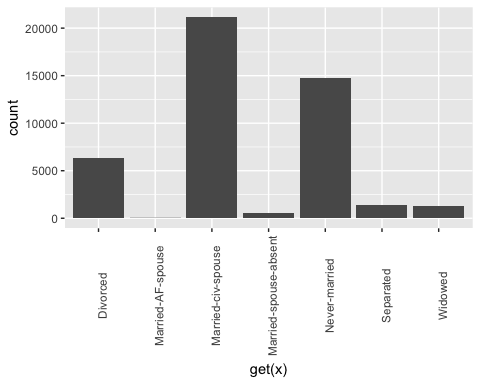
Recast Семейное положение
Также возможно создание более низких уровней для семейного положения. В следующем коде вы изменяете уровень следующим образом:
|
Старый уровень |
Новый уровень |
|---|---|
|
Никогда не был женат |
Не женат не замужем |
|
Женат, супруга, отсутствует |
Не женат не замужем |
|
Замужем-AF-супруга |
замужем |
|
Замужем-стро-супруга |
|
|
отделенный |
отделенный |
|
Разведенный |
|
|
Вдовы |
вдова |
# Change level marry recast_data <- recast_data % > % mutate(marital.status = factor(ifelse(marital.status == "Never-married" | marital.status == "Married-spouse-absent", "Not_married", ifelse(marital.status == "Married-AF-spouse" | marital.status == "Married-civ-spouse", "Married", ifelse(marital.status == "Separated" | marital.status == "Divorced", "Separated", "Widow")))))
Вы можете проверить количество людей в каждой группе.
table(recast_data$marital.status)
Вывод:
## ## Married Not_married Separated Widow ## 21165 15359 7727 1286
Шаг 4) Сводная статистика
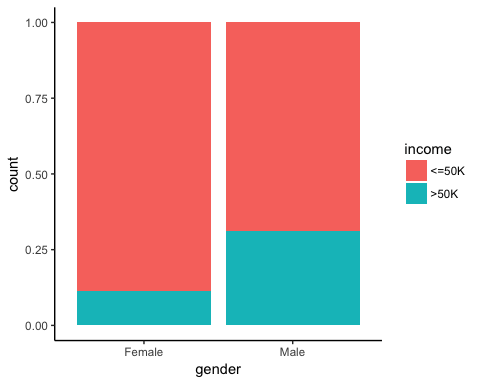
Пришло время проверить некоторые статистические данные о наших целевых переменных. На приведенном ниже графике вы считаете процент людей, заработавших более 50 000, с учетом их пола.
# Plot gender income
ggplot(recast_data, aes(x = gender, fill = income)) +
geom_bar(position = "fill") +
theme_classic()
Вывод:
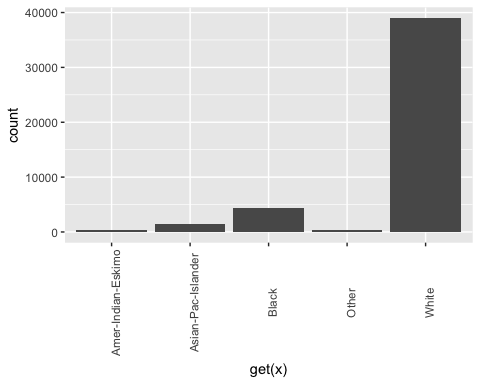
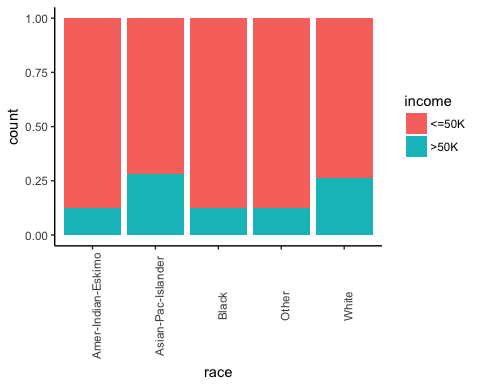
Затем, проверьте, влияет ли происхождение человека на их заработок.
# Plot origin income
ggplot(recast_data, aes(x = race, fill = income)) +
geom_bar(position = "fill") +
theme_classic() +
theme(axis.text.x = element_text(angle = 90))
Вывод:
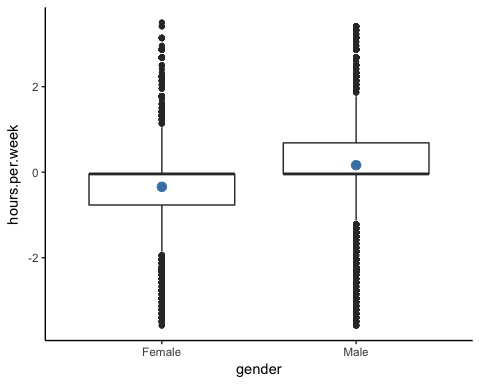
Количество часов работы по полу.
# box plot gender working time
ggplot(recast_data, aes(x = gender, y = hours.per.week)) +
geom_boxplot() +
stat_summary(fun.y = mean,
geom = "point",
size = 3,
color = "steelblue") +
theme_classic()
Вывод:
Квадратный график подтверждает, что распределение рабочего времени подходит для разных групп. На рамочном графике оба пола не имеют однородных наблюдений.
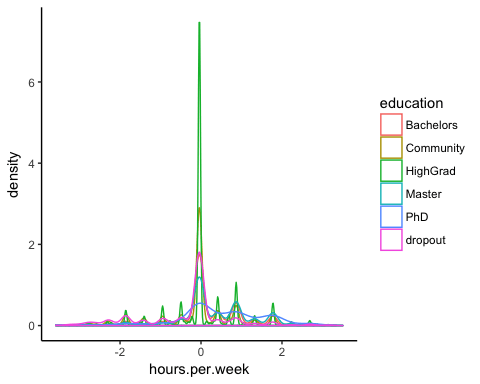
Вы можете проверить плотность еженедельного рабочего времени по типу образования. Распределения имеют много разных выборов. Вероятно, это можно объяснить типом контракта в США.
# Plot distribution working time by education
ggplot(recast_data, aes(x = hours.per.week)) +
geom_density(aes(color = education), alpha = 0.5) +
theme_classic()
Код Объяснение
- ggplot (recast_data, aes (x = hours.per.week)): для графика плотности требуется только одна переменная
- geom_density (aes (color = education), alpha = 0.5): геометрический объект для контроля плотности
Вывод:
Чтобы подтвердить свои мысли, вы можете выполнить односторонний тест ANOVA:
anova <- aov(hours.per.week~education, recast_data) summary(anova)
Вывод:
## Df Sum Sq Mean Sq F value Pr(>F) ## education 5 1552 310.31 321.2 <2e-16 *** ## Residuals 45531 43984 0.97 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Тест ANOVA подтверждает разницу в среднем между группами.
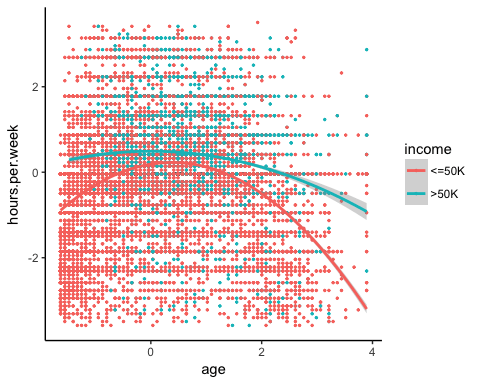
Нелинейность
Перед запуском модели вы можете увидеть, связано ли количество отработанных часов с возрастом.
library(ggplot2)
ggplot(recast_data, aes(x = age, y = hours.per.week)) +
geom_point(aes(color = income),
size = 0.5) +
stat_smooth(method = 'lm',
formula = y~poly(x, 2),
se = TRUE,
aes(color = income)) +
theme_classic()
Код Объяснение
- ggplot (recast_data, aes (x = age, y = hours.per.week)): установить эстетику графика
- geom_point (aes (цвет = доход), размер = 0.5): построить точечный график
- stat_smooth (): добавить линию тренда со следующими аргументами:
- method = ‘lm’: нанесите подгоночное значение, если линейная регрессия
- формула = y ~ poly (x, 2): подгонка полиномиальной регрессии
- se = TRUE: добавить стандартную ошибку
- aes (цвет = доход): разбить модель по доходу
Вывод:
Вкратце, вы можете протестировать условия взаимодействия в модели, чтобы уловить эффект нелинейности между рабочим временем в неделю и другими функциями. Важно определить, при каких условиях рабочее время отличается.
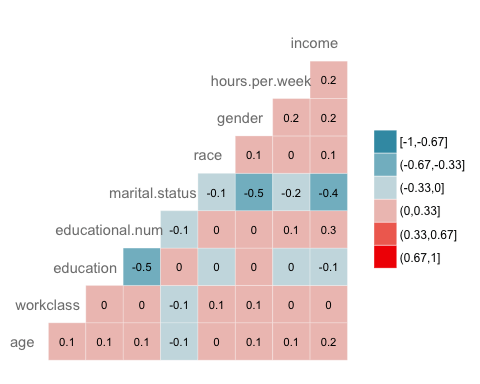
корреляция
Следующая проверка должна визуализировать корреляцию между переменными. Вы конвертируете тип уровня фактора в числовой, чтобы вы могли построить тепловую карту, содержащую коэффициент корреляции, рассчитанный по методу Спирмена.
library(GGally)
# Convert data to numeric
corr <- data.frame(lapply(recast_data, as.integer))
# Plot the graphggcorr(corr,
method = c("pairwise", "spearman"),
nbreaks = 6,
hjust = 0.8,
label = TRUE,
label_size = 3,
color = "grey50")
Код Объяснение
- data.frame (lapply (recast_data, as.integer)): преобразовать данные в числовые
- ggcorr () строит тепловую карту со следующими аргументами:
- Метод: метод для вычисления корреляции
- nbreaks = 6: количество перерывов
- hjust = 0.8: управляющая позиция имени переменной на графике
- label = TRUE: добавить метки в центре окон
- label_size = 3: размер метки
- color = «grey50»): цвет этикетки
Вывод:
Шаг 5) Поезд / тестовый набор
Любая контролируемая задача машинного обучения требует разделения данных между набором поездов и тестовым набором. Вы можете использовать «функцию», которую вы создали в других контролируемых учебных пособиях, чтобы создать набор поездов / тестов.
set.seed(1234)
create_train_test <- function(data, size = 0.8, train = TRUE) {
n_row = nrow(data)
total_row = size * n_row
train_sample <- 1: total_row
if (train == TRUE) {
return (data[train_sample, ])
} else {
return (data[-train_sample, ])
}
}
data_train <- create_train_test(recast_data, 0.8, train = TRUE)
data_test <- create_train_test(recast_data, 0.8, train = FALSE)
dim(data_train)
Вывод:
## [1] 36429 9
dim(data_test)
Вывод:
## [1] 9108 9
Шаг 6) Постройте модель
Чтобы увидеть, как работает алгоритм, вы используете пакет glm (). Обобщенная линейная модель представляет собой набор моделей. Основной синтаксис:
glm(formula, data=data, family=linkfunction() Argument: - formula: Equation used to fit the model- data: dataset used - Family: - binomial: (link = "logit") - gaussian: (link = "identity") - Gamma: (link = "inverse") - inverse.gaussian: (link = "1/mu^2") - poisson: (link = "log") - quasi: (link = "identity", variance = "constant") - quasibinomial: (link = "logit") - quasipoisson: (link = "log")
Вы готовы оценить логистическую модель, чтобы разделить уровень дохода между набором функций.
formula <- income~. logit <- glm(formula, data = data_train, family = 'binomial') summary(logit)
Код Объяснение
- формула <- доход ~.: создать модель, чтобы соответствовать
- logit <- glm (формула, data = data_train, family = ‘binomial’): согласовать логистическую модель (family = ‘binomial’) с данными data_train.
- summary (logit): распечатать сводку модели
Вывод:
## ## Call: ## glm(formula = formula, family = "binomial", data = data_train) ## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.6456 -0.5858 -0.2609 -0.0651 3.1982 ## ## Coefficients: ## Estimate Std. Error z value Pr(>|z|) ## (Intercept) 0.07882 0.21726 0.363 0.71675 ## age 0.41119 0.01857 22.146 < 2e-16 *** ## workclassLocal-gov -0.64018 0.09396 -6.813 9.54e-12 *** ## workclassPrivate -0.53542 0.07886 -6.789 1.13e-11 *** ## workclassSelf-emp-inc -0.07733 0.10350 -0.747 0.45499 ## workclassSelf-emp-not-inc -1.09052 0.09140 -11.931 < 2e-16 *** ## workclassState-gov -0.80562 0.10617 -7.588 3.25e-14 *** ## workclassWithout-pay -1.09765 0.86787 -1.265 0.20596 ## educationCommunity -0.44436 0.08267 -5.375 7.66e-08 *** ## educationHighGrad -0.67613 0.11827 -5.717 1.08e-08 *** ## educationMaster 0.35651 0.06780 5.258 1.46e-07 *** ## educationPhD 0.46995 0.15772 2.980 0.00289 ** ## educationdropout -1.04974 0.21280 -4.933 8.10e-07 *** ## educational.num 0.56908 0.07063 8.057 7.84e-16 *** ## marital.statusNot_married -2.50346 0.05113 -48.966 < 2e-16 *** ## marital.statusSeparated -2.16177 0.05425 -39.846 < 2e-16 *** ## marital.statusWidow -2.22707 0.12522 -17.785 < 2e-16 *** ## raceAsian-Pac-Islander 0.08359 0.20344 0.411 0.68117 ## raceBlack 0.07188 0.19330 0.372 0.71001 ## raceOther 0.01370 0.27695 0.049 0.96054 ## raceWhite 0.34830 0.18441 1.889 0.05894 . ## genderMale 0.08596 0.04289 2.004 0.04506 * ## hours.per.week 0.41942 0.01748 23.998 < 2e-16 *** ## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## (Dispersion parameter for binomial family taken to be 1) ## ## Null deviance: 40601 on 36428 degrees of freedom ## Residual deviance: 27041 on 36406 degrees of freedom ## AIC: 27087 ## ## Number of Fisher Scoring iterations: 6
Краткое изложение нашей модели раскрывает интересную информацию. Производительность логистической регрессии оценивается с помощью конкретных ключевых показателей.
- AIC (Akaike Information Criteria): это эквивалент R2 в логистической регрессии. Он измеряет соответствие, когда к числу параметров применяется штраф. Меньшие значения AIC указывают на то, что модель ближе к истине.
- Нулевое отклонение: соответствует модели только с перехватом. Степень свободы n-1. Мы можем интерпретировать его как значение хи-квадрат (подходящее значение, отличное от проверки гипотезы фактического значения).
- Остаточное отклонение: модель со всеми переменными. Это также интерпретируется как проверка гипотезы хи-квадрат.
- Количество итераций по шкале Фишера: количество итераций до схождения.
Вывод функции glm () сохраняется в списке. Приведенный ниже код показывает все элементы, доступные в переменной logit, которую мы создали для оценки логистической регрессии.
# Список очень длинный, выводятся только первые три элемента
lapply(logit, class)[1:3]
Вывод:
## $coefficients ## [1] "numeric" ## ## $residuals ## [1] "numeric" ## ## $fitted.values ## [1] "numeric"
Каждое значение может быть извлечено со знаком $, за которым следует имя метрики. Например, вы сохранили модель как logit. Чтобы извлечь критерии AIC, вы используете:
logit$aic
Вывод:
## [1] 27086.65
Шаг 7) Оцените производительность модели
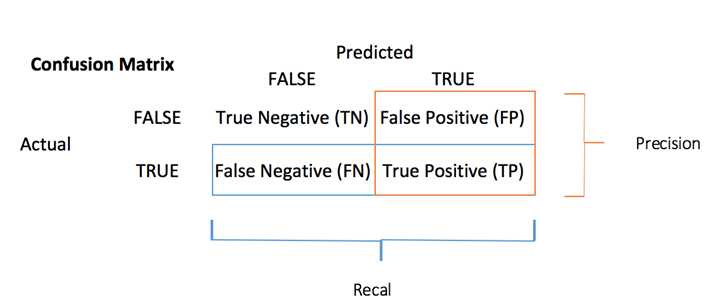
Матрица путаницы
Матрица неточностей является лучшим выбором для оценки эффективности классификации по сравнению с различными метриками вы видели раньше. Общая идея состоит в том, чтобы подсчитать, сколько раз Истинные экземпляры классифицируются как Ложные.
Чтобы вычислить матрицу путаницы, сначала необходимо иметь набор прогнозов, чтобы их можно было сравнивать с фактическими целями.
predict <- predict(logit, data_test, type = 'response') # confusion matrix table_mat <- table(data_test$income, predict > 0.5) table_mat
Код Объяснение
- Предикат (logit, data_test, type = ‘response’): вычислить прогноз на тестовом наборе. Установите type = ‘response’, чтобы вычислить вероятность ответа.
- таблица (data_test $ доход, прогноз> 0,5): вычислить матрицу путаницы. Предикат> 0,5 означает, что он возвращает 1, если прогнозируемые вероятности выше 0,5, иначе 0.
Вывод:
## ## FALSE TRUE ## <=50K 6310 495 ## >50K 1074 1229
Каждая строка в матрице путаницы представляет фактическую цель, в то время как каждый столбец представляет прогнозируемую цель. В первой строке этой матрицы рассматривается доход ниже 50 тыс. (Класс False): 6241 были правильно классифицированы как лица с доходом ниже 50 тыс. ( Истинно отрицательный ), а оставшаяся была ошибочно классифицирована как выше 50 тыс. ( Ложно положительный ). Во второй строке рассматривается доход выше 50 тыс., Положительный класс был 1229 ( истинно положительный ), а истинный отрицательный — 1074.
Вы можете рассчитать точность модели путем суммирования истинного положительного + истинного отрицательного значения по всему наблюдению
accuracy_Test <- sum(diag(table_mat)) / sum(table_mat) accuracy_Test
Код Объяснение
- сумма (diag (table_mat)): сумма диагонали
- sum (table_mat): сумма матрицы.
Вывод:
## [1] 0.8277339
Модель, кажется, страдает от одной проблемы, она переоценивает количество ложных негативов. Это называется парадоксом проверки точности . Мы указали, что точность — это отношение правильных прогнозов к общему количеству случаев. Мы можем иметь относительно высокую точность, но бесполезную модель. Это происходит, когда есть доминирующий класс. Если вы посмотрите на матрицу недоразумений, вы увидите, что большинство случаев классифицируются как истинно отрицательные. Теперь представьте, что модель классифицировала все классы как отрицательные (то есть ниже 50 КБ). Точность 75% (6718/6718 + 2257). Ваша модель работает лучше, но изо всех сил пытается отличить истинное положительное с истинным отрицательным.
В такой ситуации предпочтительно иметь более краткую метрику. Мы можем посмотреть на:
- Точность = TP / (TP + FP)
- Напомним = TP / (TP + FN)
Точность против Напомним
Точность смотрит на точность положительного прогноза. Напоминание — это соотношение положительных экземпляров, которые правильно обнаружены классификатором;
Вы можете построить две функции для вычисления этих двух метрик
- Построить точность
precision <- function(matrix) {
# True positive
tp <- matrix[2, 2]
# false positive
fp <- matrix[1, 2]
return (tp / (tp + fp))
}
Код Объяснение
- mat [1,1]: вернуть первую ячейку первого столбца фрейма данных, т.е. истинно положительный
- мат [1,2]; Вернуть первую ячейку второго столбца фрейма данных, т.е. ложное срабатывание
recall <- function(matrix) {
# true positive
tp <- matrix[2, 2]# false positive
fn <- matrix[2, 1]
return (tp / (tp + fn))
}
Код Объяснение
- mat [1,1]: вернуть первую ячейку первого столбца фрейма данных, т.е. истинно положительный
- мат [2,1]; Вернуть вторую ячейку первого столбца фрейма данных, т.е. ложный минус
Вы можете проверить свои функции
prec <- precision(table_mat) prec rec <- recall(table_mat) rec
Вывод:
## [1] 0.712877 ## [2] 0.5336518
Когда модель говорит, что это человек с весом выше 50 КБ, это верно только в 54% случаев и может претендовать на лиц с весом свыше 50 КБ в 72% случаев.
Вы можете создать 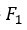
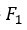
f1 <- 2 * ((prec * rec) / (prec + rec)) f1
Вывод:
## [1] 0.6103799
Точность в сравнении с отзывом
Невозможно иметь как высокую точность, так и высокую степень отзыва.
Если мы повысим точность, правильное лицо будет лучше предсказано, но мы бы пропустили многие из них (меньше отзывов). В некоторых ситуациях мы предпочитаем более высокую точность, чем вспомнить. Существует четкая связь между точностью и отзывом.
- Представьте, вам нужно предсказать, есть ли у пациента заболевание. Вы хотите быть максимально точным.
- Если вам необходимо обнаружить потенциальных мошеннических людей на улице с помощью распознавания лиц, было бы лучше поймать многих людей, помеченных как мошеннические, даже если точность низкая. Полиция сможет освободить не мошенническое лицо.
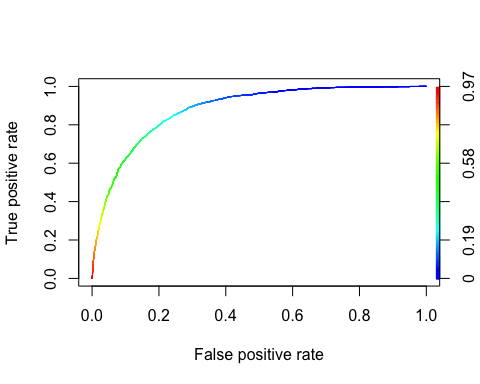
Кривая ROC
Характеристика приемник Операционный кривой является еще одним распространенным инструментом , используемым с бинарной классификацией. Она очень похожа на кривую «точность / отзыв», но вместо того, чтобы отображать точность и отзыв, кривая ROC показывает истинную положительную скорость (т.е. отзыв) по сравнению с ложной положительной скоростью. Коэффициент ложноположительных результатов — это соотношение отрицательных случаев, которые ошибочно классифицируются как положительные. Он равен единице минус истинная отрицательная ставка. Истинный отрицательный показатель также называется специфичностью . Следовательно, кривая ROC отображает чувствительность (отзыв) в сравнении с 1-специфичностью
Чтобы построить кривую ROC, нам нужно установить библиотеку под названием RORC. Мы можем найти в библиотеке conda . Вы можете ввести код:
Конда установить -cr r-rocr —yes
Мы можем построить ROC с помощью функцийpregnation () и performance ().
library(ROCR) ROCRpred <- prediction(predict, data_test$income) ROCRperf <- performance(ROCRpred, 'tpr', 'fpr') plot(ROCRperf, colorize = TRUE, text.adj = c(-0.2, 1.7))
Код Объяснение
- прогнозирование (предикат, data_test $ доход): библиотеке ROCR необходимо создать объект прогнозирования для преобразования входных данных
- Производительность (ROCRpred, ‘tpr’, ‘fpr’): возврат двух комбинаций для создания на графике. Здесь, tpr и fpr построены. Для точной прорисовки сюжета и вызова вместе используйте «prec», «rec».
Вывод:
Шаг 8) Улучшение модели
Вы можете попытаться добавить нелинейность в модель с взаимодействием между
- возраст и часы
- пол и часов.пер.нед.
Вам нужно использовать тест оценки, чтобы сравнить обе модели
formula_2 <- income~age: hours.per.week + gender: hours.per.week + . logit_2 <- glm(formula_2, data = data_train, family = 'binomial') predict_2 <- predict(logit_2, data_test, type = 'response') table_mat_2 <- table(data_test$income, predict_2 > 0.5) precision_2 <- precision(table_mat_2) recall_2 <- recall(table_mat_2) f1_2 <- 2 * ((precision_2 * recall_2) / (precision_2 + recall_2)) f1_2
Вывод:
## [1] 0.6109181
Оценка немного выше, чем предыдущая. Вы можете продолжать работать над данными, пытаясь побить рекорд.
Резюме
Мы можем суммировать функцию для обучения логистической регрессии в таблице ниже:
|
пакет |
Задача |
функция |
аргумент |
|---|---|---|---|
|
— |
Создать набор данных поезда / теста |
create_train_set () |
данные, размер, поезд |
|
GLM |
Обучите обобщенную линейную модель |
GLM () |
формула, данные, семья * |
|
GLM |
Подведите итог модели |
резюме() |
подогнанная модель |
|
база |
Сделать прогноз |
предсказать, () |
подогнанная модель, набор данных, тип = «ответ» |
|
база |
Создать матрицу путаницы |
Таблица() |
у, прогноз () |
|
база |
Создать оценку точности |
сумма (диаг (таблица ()) / сумма (таблица () |
|
|
ROCR |
Создать ROC: Шаг 1 Создать прогноз |
предсказания () |
предсказание (), у |
|
ROCR |
Создать ROC: Шаг 2 Создать производительность |
представление() |
предсказание (), ‘tpr’, ‘fpr’ |
|
ROCR |
Создать ROC: Шаг 3 График |
сюжет() |
представление() |
Другой тип моделей GLM :
— бином: (ссылка = «логит»)
— гауссовский: (ссылка = «личность»)
— Гамма: (ссылка = «обратная»)
— inverse.gaussian: (link = «1 / mu ^ 2»)
— Пуассон: (link = «log»)
— квази: (ссылка = «идентичность», дисперсия = «константа»)
— квазибином: (ссылка = «логит»)
— квазипуассон: (link = «log»)