Что такое ANOVA?
Дисперсионный анализ (ANOVA) представляет собой статистический метод, обычно используемый для изучения различий между двумя или более групповыми средними. Тест ANOVA сосредоточен на различных источниках вариации в типичной переменной. ANOVA в R в первую очередь предоставляет доказательства существования среднего равенства между группами. Этот статистический метод является продолжением t-критерия. Используется в ситуации, когда факторная переменная имеет более одной группы.
В этом уроке мы узнаем
Односторонний ANOVA
Есть много ситуаций, когда вам нужно сравнить среднее значение между несколькими группами. Например, отдел маркетинга хочет знать, имеют ли три команды одинаковые показатели продаж.
- Команда: 3 уровня фактор: A, B и C
- Продажа: показатель эффективности
Тест ANOVA может определить, имеют ли три группы одинаковые показатели.
Чтобы выяснить, поступают ли данные из одной и той же совокупности, вы можете выполнить односторонний дисперсионный анализ (далее односторонний ANOVA). Этот тест, как и любые другие статистические тесты, свидетельствует о том, может ли гипотеза H0 быть принята или отклонена.
Гипотеза в одностороннем тесте ANOVA:
- H0: средства между группами идентичны
- H3: по крайней мере, среднее значение для одной группы отличается
Другими словами, гипотеза H0 подразумевает, что недостаточно доказательств, чтобы доказать, что среднее значение группы (фактора) отличается от другого.
Этот тест похож на t-тест, хотя тест ANOVA рекомендуется в ситуации с более чем 2 группами. Кроме того, t-тест и ANOVA дают схожие результаты.
Предположения
Мы предполагаем, что каждый фактор выбирается случайным образом, независимо и происходит из нормально распределенной популяции с неизвестными, но равными отклонениями.
Интерпретировать тест ANOVA
F-статистика используется для проверки того, являются ли данные из существенно разных групп населения, т. Е. Из разных выборочных средних.
Чтобы вычислить F-статистику, вам необходимо разделить межгрупповую изменчивость на внутригрупповую изменчивость .
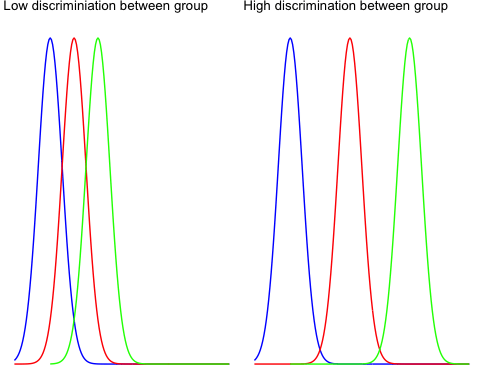
Межгрупповая изменчивость отражает различия между группами внутри всего населения. Посмотрите на два графика ниже, чтобы понять концепцию межгрупповой дисперсии.
Левый график показывает очень небольшое отклонение между тремя группами, и весьма вероятно, что три средних значения стремятся к общему среднему значению (то есть среднему значению для трех групп).
Правый график показывает три распределения далеко друг от друга, и ни одно из них не перекрывается. Существует высокая вероятность того, что разница между общим средним и средним по группам будет большой.
В группе вариабельность считает разницу между группами. Изменение происходит от индивидуальных наблюдений; некоторые точки могут быть совершенно другими, чем групповые. В группе вариабельность подхватывает этот эффект и относится к погрешности выборки.
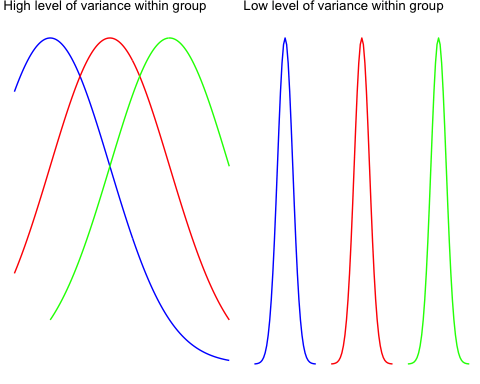
Чтобы визуально понять концепцию внутригрупповой изменчивости, посмотрите на график ниже.
Левая часть показывает распределение трех разных групп. Вы увеличили разброс каждого образца, и стало ясно, что индивидуальная дисперсия велика. F-критерий уменьшится, что означает, что вы склонны принимать нулевую гипотезу
Правая часть показывает точно такие же образцы (идентичное среднее), но с меньшей вариабельностью. Это приводит к увеличению F-теста и имеет тенденцию в пользу альтернативной гипотезы.
Вы можете использовать обе меры для построения F-статистики. Это очень интуитивно понятно для F-статистики. Если числитель увеличивается, это означает, что изменчивость между группами высока, и вполне вероятно, что группы в выборке взяты из совершенно разных распределений.
Другими словами, низкая F-статистика указывает на небольшую или нулевую разницу между средними по группе.
Пример One way ANOVA Test
Вы будете использовать набор отравленных данных для реализации одностороннего теста ANOVA. Набор данных содержит 48 строк и 3 переменные:
- Время: время выживания животного
- Яд: Тип используемого яда: уровень фактора: 1,2 и 3
- лакомство: тип используемого лечения: уровень фактора: 1,2 и 3
Прежде чем вы начнете вычислять тест ANOVA, вам необходимо подготовить данные следующим образом:
- Шаг 1: Импортируйте данные
- Шаг 2: Удалите ненужную переменную
- Шаг 3: Преобразуйте переменный яд как упорядоченный уровень
library(dplyr) PATH <- "https://raw.githubusercontent.com/guru99-edu/R-Programming/master/poisons.csv" df <- read.csv(PATH) %>% select(-X) %>% mutate(poison = factor(poison, ordered = TRUE)) glimpse(df)
Вывод:
## Observations: 48 ## Variables: 3 ## $ time <dbl> 0.31, 0.45, 0.46, 0.43, 0.36, 0.29, 0.40, 0.23, 0.22, 0... ## $ poison <ord> 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 1, 1, 1, 1, 2, 2, 2... ## $ treat <fctr> A, A, A, A, A, A, A, A, A, A, A, A, B, B, B, B, B, B, ...
Наша цель — проверить следующее предположение:
- H0: нет разницы в среднем времени выживания между группами
- H3: среднее время выживания отличается по крайней мере для одной группы.
Другими словами, вы хотите знать, существует ли статистическая разница между средним значением времени выживания в зависимости от типа яда, даваемого морской свинке.
Вы будете действовать следующим образом:
- Шаг 1: Проверьте формат переменной яд
- Шаг 2: Распечатать сводную статистику: количество, среднее и стандартное отклонение
- Шаг 3: нанесите коробочный график
- Шаг 4: Вычислить односторонний тест ANOVA
- Шаг 5: Запустите попарный t-тест
Step 1) You can check the level of the poison with the following code. You should see three character values because you convert them in factor with the mutate verb.
levels(df$poison)
Output:
## [1] "1" "2" "3"
Step 2) You compute the mean and standard deviation.
df % > % group_by(poison) % > % summarise( count_poison = n(), mean_time = mean(time, na.rm = TRUE), sd_time = sd(time, na.rm = TRUE) )
Output:
## # A tibble: 3 x 4 ## poison count_poison mean_time sd_time ## <ord> <int> <dbl> <dbl> ## 1 1 16 0.617500 0.20942779 ## 2 2 16 0.544375 0.28936641 ## 3 3 16 0.276250 0.06227627
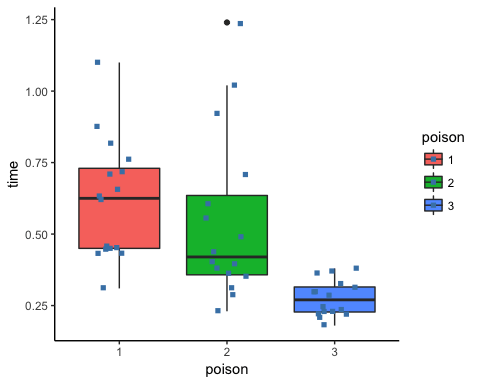
Step 3) In step three, you can graphically check if there is a difference between the distribution. Note that you include the jittered dot.
ggplot(df, aes(x = poison, y = time, fill = poison)) +
geom_boxplot() +
geom_jitter(shape = 15,
color = "steelblue",
position = position_jitter(0.21)) +
theme_classic()
Output:
Step 4) You can run the one-way ANOVA test with the command aov. The basic syntax for an ANOVA test is:
aov(formula, data) Arguments: - formula: The equation you want to estimate - data: The dataset used
The syntax of the formula is:
y ~ X1+ X2+...+Xn # X1 + X2 +... refers to the independent variables y ~ . # use all the remaining variables as independent variables
Вы можете ответить на наш вопрос: есть ли разница во времени выживания морской свинки, зная тип выданного яда.
Обратите внимание, что рекомендуется сохранить модель и использовать функцию summary (), чтобы лучше распечатать результаты.
anova_one_way <- aov(time~poison, data = df) summary(anova_one_way)
Код Объяснение
- aov (время ~ яд, данные = df): запустить тест ANOVA по следующей формуле
- summary (anova_one_way): распечатать сводку теста
Вывод:
## Df Sum Sq Mean Sq F value Pr(>F) ## poison 2 1.033 0.5165 11.79 7.66e-05 *** ## Residuals 45 1.972 0.0438 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Значение р ниже обычного порога 0,05. Вы можете с уверенностью сказать, что существует статистическая разница между группами, обозначенная «*».
Парное сравнение
Односторонний тест ANOVA не сообщает, какая группа имеет другое среднее значение. Вместо этого вы можете выполнить тест Tukey с помощью функции TukeyHSD ().
TukeyHSD(anova_one_way)
Вывод:
Двухсторонний ANOVA
Двусторонний тест ANOVA добавляет в формулу еще одну групповую переменную. Он идентичен одностороннему тесту ANOVA, хотя формула слегка меняется:
с является количественной переменной и и являются категориальными переменными.
Гипотеза в двухстороннем тесте ANOVA:
- H0: Средние значения равны для обеих переменных (т. Е. Факторная переменная)
- H3: средства различны для обеих переменных
Вы добавляете переменную обращения к нашей модели. Эта переменная указывает на лечение, назначенное морской свинке. Вам интересно узнать, существует ли статистическая зависимость между ядом и лечением, которое дает морская свинка.
Мы корректируем наш код, добавляя лакомство с другой независимой переменной.
anova_two_way <- aov(time~poison + treat, data = df) summary(anova_two_way)
Вывод:
## Df Sum Sq Mean Sq F value Pr(>F) ## poison 2 1.0330 0.5165 20.64 5.7e-07 *** ## treat 3 0.9212 0.3071 12.27 6.7e-06 *** ## Residuals 42 1.0509 0.0250 ## ---
Вы можете заключить, что и яд, и лечение статистически отличаются от 0. Вы можете отклонить гипотезу NULL и подтвердить, что изменение лечения или яда влияет на время выживания.
Резюме
Мы можем подвести итоги теста в таблице ниже:
|
Тестовое задание |
код |
гипотеза |
р-значение |
|---|---|---|---|
|
One way ANOVA |
aov(y ~ X, data = df) |
H3: среднее значение отличается по крайней мере для одной группы |
0,05 |
|
парный |
TukeyHSD(ANOVA summary) |
0,05 |
|
|
Двухсторонний анова |
aov(y ~ X1 + X2, data = df) |
H3: среднее значение отличается для обеих групп |
0,05 |