Параметр Хаббла и масштабный коэффициент

В этой главе мы обсудим как параметр Хаббла, так и коэффициент масштабирования.

• Обязательное условие — космологическое красное смещение, космологические принципы.

• Предположение — Вселенная однородна и изотропна.

Обязательное условие — космологическое красное смещение, космологические принципы.

Предположение — Вселенная однородна и изотропна.

Константа Хаббла с дробной скоростью изменения масштабного коэффициента

В этом разделе мы будем связывать постоянную Хаббла с частичной скоростью изменения коэффициента масштабирования.

Мы можем записать скорость следующим образом и упростить.

$$v = \ frac {\ mathrm {d} r_p} {\ mathrm {d} t}$$

$$= \ frac {d [a (t) r_c} {dt}$$

$$v = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ ast \ frac {1} {a} \ ast (ar_c)$$

$$v = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ ast \ frac {1} {a} \ ast r_p$$

Здесь v — скорость спада, a — коэффициент масштабирования, а r _p — правильное расстояние между галактиками.

Эмпирическая формула Хаббла имела природу —

$$v = H \ ast r_p$$

Таким образом, сравнивая два приведенных выше уравнения, получаем:

Параметр Хаббла = Дробная скорость изменения масштабного коэффициента

$$H = da / dt \ ast 1 / a$$

Примечание. Это не постоянная величина, поскольку масштабный коэффициент является функцией времени. Следовательно, это называется параметром Хаббла, а не постоянной Хаббла.

Опытным путем мы пишем —

$$H = V / D$$

Таким образом, из этого уравнения мы можем сделать вывод, что, поскольку D увеличивается, а V является константой, то H уменьшается со временем и расширением Вселенной.

Уравнение Фридмана в связи с моделью Робертсона-Уокера

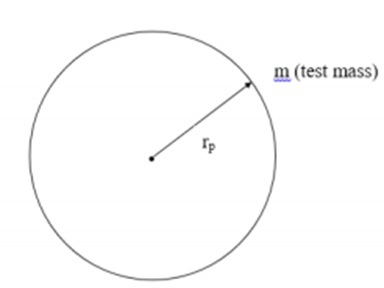
В этом разделе мы поймем, как используется уравнение Фридмана в сочетании с моделью Робертсона-Уокера. Чтобы понять это, возьмем в качестве примера следующее изображение, на котором испытательная масса находится на расстоянии r _p от массы M.

Принимая во внимание вышеприведенное изображение, мы можем выразить силу как —

$$F = G \ ast M \ ast \ frac {m} {r ^ 2_p}$$

Здесь G — универсальная гравитационная постоянная, а ρ — плотность вещества внутри наблюдаемой вселенной.

Теперь, предполагая однородную плотность массы внутри сферы, мы можем написать —

$$M = \ frac {4} {3} \ ast \ pi \ ast r_p ^ 3 \ ast \ rho$$

Используя их обратно в нашем уравнении силы, мы получаем —

$$F = \ frac {4} {3} \ ast \ pi \ ast G \ ast r_p \ ast \ rho \ ast m$$

Таким образом, мы можем записать потенциальную энергию и кинетическую энергию массы m как —

$$V = - \ frac {4} {3} \ ast \ pi \ ast G \ ast r ^ 2_p \ ast m \ ast \ rho$$

$$KE = \ frac {1} {2} \ ast m \ ast \ frac {\ mathrm {d} r_p ^ 2} {\ mathrm {d} t}$$

Используя теорему вириала —

$$U = KE + V$$

$$U = \ frac {1} {2} \ ast m \ ast \ left (\ frac {\ mathrm {d} r_p} {\ mathrm {d} t} \ right) ^ 2 - \ frac {4} { 3} \ ast \ pi \ ast G \ ast r_p ^ 2 \ ast m \ ast \ rho$$

Но здесь, $r_p = ar_c$. Итак, мы получаем —

$$U = \ frac {1} {2} \ ast m \ ast \ left (\ frac {\ mathrm {d} a} {\ mathrm {d} t} \ right) ^ 2 r_c ^ 2 - \ frac { 4} {3} \ ast \ pi \ ast G \ ast r_p ^ 2 \ ast m \ ast \ rho$$

При дальнейшем упрощении получим уравнение Фридмана,

$$\ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} \ ast G \ ast \ rho + \ frac {2U} {m} \ ast r_c ^ 2 \ ast a ^ 2$$

Здесь U постоянная. Также отметим, что во вселенной, в которой мы живем в настоящее время, преобладает материя, а плотность энергии излучения очень мала.

Параметр Хаббла уменьшается со временем и расширением Вселенной.

В настоящее время во вселенной, в которой мы живем, доминирует материя, а плотность энергии излучения очень низкая.