Красное смещение и рецессивная скорость

Наблюдения Хаббла использовали тот факт, что лучевая скорость связана со смещением спектральных линий . Здесь мы увидим четыре случая и найдем связь между рецессивной скоростью ($v_r$) и красным смещением (z).

Случай 1: нерелятивистский случай перемещения источника

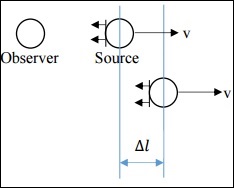
В этом случае v намного меньше, чем c. Источник излучает некоторый сигнал (звук, свет и т. Д.), Который распространяется в виде волновых фронтов . Интервал времени между отправкой двух последовательных сигналов в исходном кадре составляет Δts . Интервал времени между приемом двух последовательных сигналов в кадре наблюдателя составляет Δto .

Если и наблюдатель, и источник неподвижны, тогда Δts = Δto, но здесь это не так. Вместо этого отношение выглядит следующим образом.

$$\ Delta t_o = \ Delta t_s + \ frac {\ Delta l} {c}$$

Теперь $\ Delta l = v \ Delta t_s$

Кроме того, так как (скорость волны х время) = длина волны, мы получаем

$$\ frac {\ Delta t_o} {\ Delta t_s} = \ frac {\ lambda_o} {\ lambda_s}$$

Из приведенных выше уравнений получаем следующее соотношение —

$$\ frac {\ lambda_o} {\ lambda_s} = 1 + \ frac {v} {c}$$

где $\ lambda _s$ — длина волны сигнала в источнике, а $\ lambda _o$ — длина волны сигнала в интерпретации наблюдателя.

Здесь, поскольку источник удаляется от наблюдателя, v является положительным.

Красное смещение —

$$z = \ frac {\ lambda_o - \ lambda_s} {\ lambda_s} = \ frac {\ lambda_o} {\ lambda_s} - 1$$

Из приведенных выше уравнений получаем красное смещение следующим образом.

$$z = \ frac {v} {c}$$

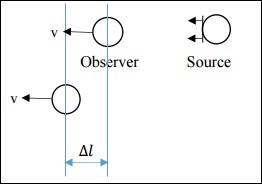
Случай 2: нерелятивистский случай перемещения наблюдателя

В этом случае v намного меньше, чем c. Здесь $\ Delta l$ отличается.

$$\ Delta l = v \ Delta t_o$$

По упрощению получаем:

$$\ frac {\ Delta t_o} {\ Delta t_s} = \ left (1 - \ frac {v} {c} \ right) ^ {- 1}$$

Мы получаем красное смещение следующим образом —

$$z = \ frac {v / c} {1-v / c}$$

Поскольку v << c , выражение красного смещения как для случая I, так и для случая II примерно одинаково.

Давайте посмотрим, как отличаются красные смещения, полученные в двух вышеупомянутых случаях.

$$z_ {II} - z_I = \ frac {v} {c} \ left [\ frac {1} {1 - v / c} -1 \ right]$$

Следовательно, $z_ {II} - z_ {I}$ — очень небольшое число из-за фактора $(v / c) ^ 2$.

Это означает, что, если v << c, мы не можем определить, движется ли источник или движется наблюдатель.

Давайте теперь поймем Основы СТО (Специальная Теория Относительности) —

• Скорость света постоянна.

• Когда источник (или наблюдатель) движется со скоростью, сравнимой со скоростью света, наблюдаются релятивистские эффекты.

• Время замедления: $\ Delta t_o = \ gamma \ Delta t_s$

• Сокращение длины: $\ Delta l_o = \ Delta t_s / \ gamma$

• Здесь $\ gamma$ — фактор Лоррентца , больше 1.

Скорость света постоянна.

Когда источник (или наблюдатель) движется со скоростью, сравнимой со скоростью света, наблюдаются релятивистские эффекты.

Время замедления: $\ Delta t_o = \ gamma \ Delta t_s$

Сокращение длины: $\ Delta l_o = \ Delta t_s / \ gamma$

Здесь $\ gamma$ — фактор Лоррентца , больше 1.

$$\ gamma = \ frac {1} {\ sqrt {1- (v ^ 2 / c ^ 2)}}$$

Случай 3: релятивистский случай перемещения источника

В этом случае v сравнимо с c. См. Тот же рисунок, что и в случае I. Из-за релятивистского эффекта наблюдается замедление времени и, следовательно, получается следующее соотношение. (Источник движется с релятивистской скоростью)

$$\ Delta t_o = \ gamma \ Delta t_s + \ frac {\ Delta l} {c}$$

$$\ Delta l = \ frac {v \ gamma \ Delta t_s} {c}$$

$$\ frac {\ Delta t_o} {\ Delta t_s} = \ frac {1 + v / c} {\ sqrt {1- (v ^ 2 / c ^ 2)}}$$

При дальнейшем упрощении получаем,

$$1 + z = \ sqrt {\ frac {1 + v / c} {1-v / c}}$$

Вышеупомянутое выражение известно как выражение кинематического доплеровского сдвига .

Случай 4: релятивистский случай перемещения наблюдателя

См. Тот же рисунок, что и в случае II. Из-за релятивистского эффекта наблюдается сокращение времени и, следовательно, получается следующее соотношение. (Наблюдатель движется с релятивистской скоростью)

$$\ Delta t_o = \ frac {\ Delta t_s} {\ gamma} + \ frac {\ Delta l} {c}$$

$$\ Delta l = \ frac {v \ Delta t_o} {c}$$

$$\ frac {\ Delta t_o} {\ Delta t_s} = \ frac {\ sqrt {1- (v ^ 2 / c ^ 2)}} {1-v / c}$$

При дальнейшем упрощении получим —

$$1 + z = \ sqrt {\ frac {1+ v / c} {1-v / c}}$$

Вышеупомянутое выражение совпадает с тем, что мы получили для случая III.

Спад скорости и красное смещение звезды являются связанными величинами.

В нерелятивистском случае мы не можем определить, является ли источник движущимся или стационарным.

В релятивистском случае нет различий в соотношении скорости красного смещения к спаду для движения источника или наблюдателя.

Движущиеся часы движутся медленнее, это прямой результат теории относительности.