Космология — метод лучевой скорости

В предыдущей главе метод радиальной скорости для случая, когда плоскость орбиты и плоскость неба перпендикулярны, обсуждался для круговых орбит. Здесь мы имеем дело с еще одним случаем, когда плоскость орбиты и плоскость неба не перпендикулярны круговым орбитам.

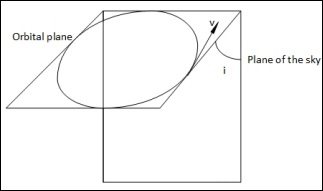
Когда плоскость орбиты находится под углом относительно плоскости неба (не перпендикулярно), мы имеем следующую ситуацию:

В этом случае, когда они были перпендикулярны, у нас было две точки, в которых мы могли измерить истинную скорость. Но здесь это невозможно. Во всех точках мы можем измерить только компонент истинной скорости v .

vr=vsin(i)cos( theta) $$v_r = v \: sin (i) cos (\ theta)$$

где θ — фаза орбиты, которая зависит от времени. Угол наклона i, с другой стороны, не зависит от времени. Следовательно,

(vr)max=vsin(i) $$(v_r) _ {max} = v \: sin (i)$$

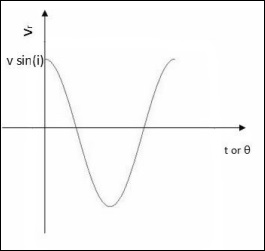
Наблюдаемая кривая лучевой скорости будет иметь следующий вид —

Когда орбитальная плоскость перпендикулярна небу —

$$ m_p = \ left (\ frac {P} {2 \ pi G} \ right) ^ {\ frac {1} {3}} (M_ \ ast) ^ {\ frac {2} {3}} v $ $

где m _p , P, G, M ∗ — масса планеты, период обращения, универсальная гравитационная постоянная и масса звезды соответственно. Но в этом случае мы должны изменить его следующим образом:

$$m_psin (i) = \ left (\ frac {P} {2 \ pi G} \ right) ^ {\ frac {1} {3}} (M_ \ ast) ^ {\ frac {2} {3} } (v_r) _ {макс}$$

Но найти значение i — трудная задача. Мы можем наложить определенные ограничения на значение i, используя метод транзита. Прохождение планеты между звездой и Землей называется транзитом. Мы можем получить кривую блеска, наблюдая транзит, и значительный провал в наблюдаемом потоке кривой блеска означает, что i близко к 90 градусам. Если такие условия не выполняются, мы не можем иметь никакого представления о значении i . Тогда найденное нами значение m _p может служить нижним пределом для массы планеты, поскольку на самом деле это m _p sin (i) и sin (i) ≤ 1 .

В заключение следует сказать, что метод радиальной скорости более удобен, чем метод транзита, поскольку радиальную скорость можно измерить в любое время, но измерения транзита можно проводить только во время транзита, который может длиться недолго.

Определение угла наклона орбиты планеты не достигается методом радиальной скорости.

Метод радиальной скорости лучше, чем метод транзита, потому что радиальная скорость может быть измерена всегда в отличие от транзита.

Транзиты недолговечны и их очень легко пропустить.