Космология — Транзитный метод

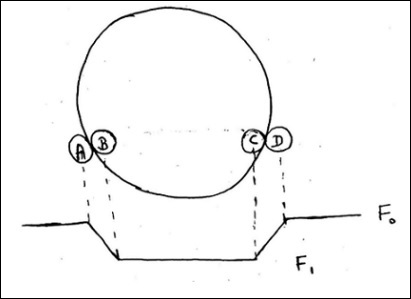
Метод Транзита (Космический телескоп Кеплера) используется, чтобы узнать размер. Падение яркости звезды на планете обычно очень мало в отличие от двойной системы.

• F ₀ — поток звезды до того, как планета закроет ее.

• F ₁ — поток после того, как вся планета находится перед звездой.

F ₀ — поток звезды до того, как планета закроет ее.

F ₁ — поток после того, как вся планета находится перед звездой.

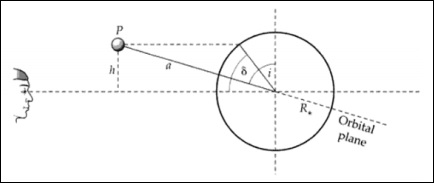
Следующее изображение будет использоваться для всех расчетов.

 fracF0−F1F0= frac pir2p piR2 ast

$$\ frac {F_0 - F_1} {F_0} = \ frac {\ pi r_p ^ {2}} {\ pi R ^ 2_ \ ast}$$

 frac DeltaFF cong fracr2pR2 ast

$$\ frac {\ Delta F} {F} \ cong \ frac {r ^ 2_p} {R ^ 2_ \ ast}$$

 left( frac DeltaFF right)earth cong0.001%

$$\ left (\ frac {\ Delta F} {F} \ right) _ {earth} \ cong 0.001 \%$$

 left( frac DeltaFF right)jupiter cong1%

$$\ left (\ frac {\ Delta F} {F} \ right) _ {jupiter} \ cong 1 \%$$

Этого нелегко достичь с помощью наземного телескопа. Это достигается телескопом Хаббла.

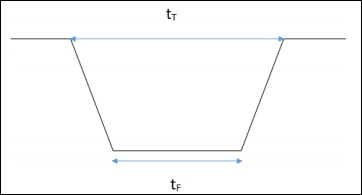
Здесь tT$t_T$ — это время между позициями A и D, а tF$t_F$ — это время между позициями B и C.

Геометрия транзита связана с наклоном i системы. Транзитная широта и наклон взаимозаменяемы.

Из приведенных выше изображений мы можем написать —

 fracha=cos(i)

$$\ frac {h} {a} = cos (i)$$

 frachR ast=sin( delta)

$$\ frac {h} {R_ \ ast} = sin (\ delta)$$

cos(i)= fracR astsin( delta)a

$$cos (i) = \ frac {R_ \ ast sin (\ delta)} {a}$$

y2=(R ast+Rp)2−h2

$$y ^ 2 = (R_ \ ast + R_p) ^ 2 - h ^ 2$$

y=[(R ast+Rp)2−h2] frac12

$$y = [(R_ \ ast + R_p) ^ 2 - h ^ 2] ^ {\ frac {1} {2}}$$

sin( theta)= fracya

$$sin (\ theta) = \ frac {y} {a}$$

 theta=sin−1 left[ frac(R ast+Rp)2−a2cos2(i)a2 right] frac12

$$\ theta = sin ^ {- 1} \ left [\ frac {(R_ \ ast + R_p) ^ 2 - a ^ 2cos ^ 2 (i)} {a ^ 2} \ right] ^ {\ frac {1 } {2}}$$

tT= fracP2 pi times2 theta

$$t_T = \ frac {P} {2 \ pi} \ times 2 \ theta$$

Здесь tT$t_T$ — это доля периода времени, в течение которого происходит транзит, а (2θ / 2π) — это доля угла, для которой происходит транзит.

sin( fractT piP)= fracR asta left[ left(1+ fracRpR ast right)2− left( fracaR astcos(i) right)2 right] frac12

$$sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1+ \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos (i) \ right) ^ 2 \ right] ^ {\ frac {1} {2}}$$

Обычно a >> R ∗ >> Rp. Итак, мы можем написать —

sin( fractT piP)= fracR asta left[1− left( fracaR astcos(i) right))2 right] frac12

$$sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [1- \ left (\ frac {a} {R_ \ ast} cos (i) \ right) ) ^ 2 \ right] ^ {\ frac {1} {2}}$$

Здесь P — продолжительность между двумя последовательными транзитами. Время прохождения очень меньше по сравнению с орбитальным периодом времени. Следовательно,

tT= fracP pi left[ left( fracR asta right)2−cos2(i) right] frac12

$$t_T = \ frac {P} {\ pi} \ left [\ left (\ frac {R_ \ ast} {a} \ right) ^ 2 - cos ^ 2 (i) \ right] ^ {\ frac {1 } {2}}$$

Здесь t _T , P, R ∗ — наблюдаемые, a и i следует выяснить.

Сейчас,

sin( fractF piP)= fracR asta left[ left(1− fracRpR ast right)2− left( fracaR astcosi right)2 right] frac12

$$sin (\ frac {t_F \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1 - \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos \: i \ right) ^ 2 \ right] ^ {\ frac {1} {2}}$$

где y2=(R ast−Rp)2−h2$y ^ 2 = (R_ \ ast - R_p) ^ 2 - h ^ 2$.

Позволять,

 frac DeltaFF=D= left( fracRpR ast right)2

$$\ frac {\ Delta F} {F} = D = \ left (\ frac {R_p} {R_ \ ast} \ right) ^ 2$$

Теперь мы можем выразить,

 fracaR ast= frac2P piD frac14(t2T−t2F)− frac12

$$\ frac {a} {R_ \ ast} = \ frac {2P} {\ pi} D ^ {\ frac {1} {4}} (t ^ 2_T - t ^ 2_F) ^ {- \ frac {1 } {2}}$$

Для звезд главной последовательности,

R ast proptoM alpha ast

$$R_ \ ast \ propto M ^ \ alpha_ \ ast$$

 fracR astR0 propto left( fracM astM0 right) alpha

$$\ frac {R_ \ ast} {R_0} \ propto \ left (\ frac {M_ \ ast} {M_0} \ right) ^ \ alpha$$

Это дает R ∗ .

Следовательно, мы также получаем значение «а».

Итак, мы получаем «R _p », «ap» и даже «i».

Для всего этого,

h leqR ast+Rp

$$h \ leq R_ \ ast + R_p$$

acosi leqR ast+Rp

$$a \: cos \: i \ leq R_ \ ast + R_p$$

Даже при ? ~ 89 градусов длительность транзита очень мала. Планета должна быть очень близко, чтобы получить достаточное время прохождения. Это дает жесткое ограничение на «я». Как только мы получим «i», мы можем вывести «m _p » из измерения радиальной скорости.

Это обнаружение методом транзита называется случайным обнаружением, то есть вероятностью наблюдения транзита. Расчеты транзитной вероятности (вероятности наблюдения) приведены ниже.

Вероятность прохождения связана с телесным углом, отслеживаемым двумя крайними конфигурациями прохождения, который:

Solidangleofplanet=2 pi left( frac2R asta right)

$$Solid \: angle \: of \: planet \: = 2 \ pi \ left (\ frac {2R_ \ ast} {a} \ right)$$

А также общий телесный угол на большой полуоси а или —

Solidangleof :phere=4 pi

$$Solid \: angle \: of \ :phere \: = \: 4 \ pi$$

Вероятность — это отношение этих двух областей:

= fracобластьofнебопокрытаяbyблагоприятнаяориентацияобластьofнебозакрытаяbyвсевозможнаяориентацияoforbit

$$= \: \ frac {область \: of \: небо \: покрытая \: by \: благоприятная \: ориентация} {область \: of \: небо \: закрытая \: by \: все \: возможная \: ориентация \: of \: orbit}$$

= frac4 piapR ast4 pia2p= fracR astap$= \ frac {4 \ pi a_pR_ \ ast} {4 \ pi a ^ 2_p} = \ frac {R_ \ ast} {a_p}$  fracareaofhollowcyclinderarea :of :phere$\ frac {area \: of \: hollow \: cyclinder} {area \ : of \ :phere}$

Эта вероятность не зависит от наблюдателя.