Космология — Вселенная с радиационным доминированием

В этой главе мы обсудим решения уравнений Фридмана, относящиеся к доминирующей радиации Вселенной. Сначала мы сравниваем плотность энергии вещества с энергией излучения. Это позволит нам увидеть, преобладает ли в нашей вселенной материя или радиация.

Энергетическая плотность излучения

Звездное излучение, распространенное в современной вселенной, очень мало можно отнести к звездным источникам, но в основном это связано с остаточным CMB (космический микроволновый фон).

Плотность энергии излучения,  epsilon gamma,0$\ epsilon _ {\ gamma, 0}$, можно выразить следующим образом:

 epsilon gamma,0=aT40

$$\ epsilon _ {\ gamma, 0} = aT_0 ^ 4$$

Здесь a — постоянная излучения, которая имеет выражение (8 pi5k4B)/(15h3c2)$(8 \ pi ^ 5k_B ^ 4) / (15h ^ 3c ^ 2)$, равное a = 7,5657 × 10 ⁻¹⁵ эрг \: см ⁻³ К ⁻⁴ . Температура T0, которую мы здесь рассматриваем, соответствует температуре черного тела, соответствующей CMB.

Подставляя результаты, имеем,

 epsilon gamma,0=aT40=4 times10−13эргсм−3

$$\ epsilon _ {\ gamma, 0} = aT_0 ^ 4 = 4 \ times 10 ^ {- 13} эрг \: см ^ {- 3}$$

Энергетическая плотность вещества

В следующих вычислениях мы предполагаем работу с плоской вселенной и K = 0. Мы рассматриваем плотность энергии вещества как  epsilon= rhoc2$\ epsilon = \ rho c ^ 2$. Мы считаем следующее —

 rhom,0c2=0.3 rhoc,0c2=0.3 times frac3H208 piG timesc2

$$\ rho_ {m, 0} c ^ 2 = 0.3 \ rho_ {c, 0} c ^ 2 = 0.3 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2$$

 rhom,0c2 simeq2 times10−8эргсм−3

$$\ rho_ {m, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 8} эрг \: см ^ {- 3}$$

 rhob,0c2=0,03 rhoc,0c2=0,03 times frac3H208 piG timesc2

$$\ rho_ {b, 0} c ^ 2 = 0,03 \ rho_ {c, 0} c ^ 2 = 0,03 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2$$

 rhob,0c2 simeq2 times10−9эргсм−3

$$\ rho_ {b, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 9} эрг \: см ^ {- 3}$$

Таким образом, из приведенного выше расчета мы видим, что мы живем во вселенной, в которой доминирует материя. Это может быть подтверждено тем фактом, что CMB очень холодный. Если мы оглянемся назад во времени, то температура CMB станет выше, и мы сможем сделать вывод, что, возможно, была эпоха, когда во Вселенной преобладала радиация.

Изменение плотности и масштабного коэффициента

Уравнение жидкости показывает нам, что —

 dot rho+3 frac dotaa left( rho+ fracPc2 right)=0

$$\ dot {\ rho} + 3 \ frac {\ dot {a}} {a} \ left (\ rho + \ frac {P} {c ^ 2} \ right) = 0$$

Если мы рассмотрим пыльную вселенную, у нас будет P = 0. Если отбросить предыдущие результаты, мы считаем, что во вселенной преобладает излучение.

 dot rhorad+3 frac dotaa left( rhorad+ fracPc2 right)=0

$$\ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {P} {c ^ 2} \ right) = 0$$

Используя соотношение давления Prad= rhoc2/3$P_ {rad} = \ rho c ^ {2/3}$, мы имеем —

 dot rhorad+3 frac dotaa left( rhorad+ frac rhorad3 right)=0

$$\ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {\ rho_ {rad}} {3} \ right) = 0$$

 dot rhorad+4 frac dotaa( rhorad)=0

$$\ dot {\ rho} _ {rad} + 4 \ frac {\ dot {a}} {a} (\ rho_ {rad}) = 0$$

О дальнейшем упрощении имеем,

 frac1a4 frac mathrmd mathrmdt( rhorada4)=0

$$\ frac {1} {a ^ 4} \ frac {\ mathrm {d}} {\ mathrm {d} t} (\ rho_ {rad} a ^ 4) = 0$$

 rhorada4=постоянная

$$\ rho_ {rad} a ^ 4 = \: постоянная$$

 rhorad propto frac1a4

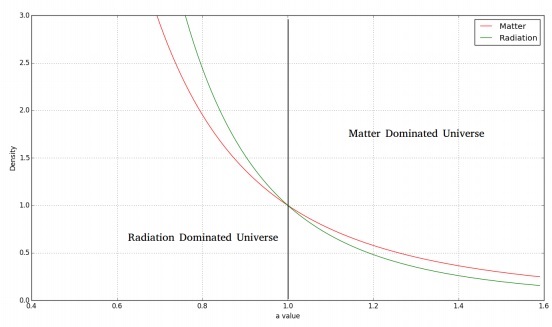
$$\ rho_ {rad} \ propto \ frac {1} {a ^ 4}$$

Приведенный выше результат показывает обратное 4- ^е изменение степени a с  rho$\ rho$.

Это может быть физически истолковано как a−3$a ^ {- 3}$, поступающее от изменения объема по мере его увеличения. Оставшиеся a−1$a ^ {- 1}$ можно рассматривать как энергию, потерянную фотоном из-за расширения пространства во вселенной (космологическое красное смещение 1 + z = a ^-1 ).

На следующем изображении показано изменение плотности вещества и излучения во времени.

Для плоской вселенной, в которой доминирует излучение, мы бы получили уравнение Фридмана следующим образом:

 left( frac dotaa right)2= frac8 piG rho3

$$\ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3}$$

 left( frac dotaa right)2= frac8 piG3 frac rho0a4

$$\ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ frac {\ rho_0} {a ^ 4}$$

При упрощении и применении решения к дифференциальному уравнению имеем:

( dota)2= frac8 piG rho03a2

$$(\ dot {a}) ^ 2 = \ frac {8 \ pi G \ rho_0} {3a ^ 2}$$

 Rightarrowa(t) proptot frac12

$$\ Rightarrow a (t) \ propto t ^ {\ frac {1} {2}}$$

Таким образом, мы имеем —

a(t)=a0 left( fractt0 right) frac12

$$a (t) = a_0 \ left (\ frac {t} {t_0} \ right) ^ {\ frac {1} {2}}$$

Из приведенного выше уравнения мы видим, что скорость увеличения масштабного коэффициента меньше, чем у пыльной вселенной.

Излучение, распространенное в современной вселенной, очень мало можно отнести к звездным источникам.

Для пыльной вселенной давление равно нулю.

CMB очень холодно.