Космология — Вселенная, в которой господствует материя

В этой главе мы обсудим решения уравнений Фридмана, касающиеся материи, в которой доминирует Вселенная. В космологии, поскольку мы видим все в больших масштабах, солнечные системы, галактики, все происходит как частицы пыли (это то, что мы видим своими глазами), мы можем назвать это пыльной вселенной или материей только вселенной.

В уравнении жидкости ,

$$\ dot {\ rho} = -3 \ left (\ frac {\ dot {a}} {a} \ right) \ rho -3 \ left (\ frac {\ dot {a}} {a} \ right ) \ left (\ frac {P} {c ^ 2} \ right)$$

Мы можем видеть, что есть термин давления. Для пыльной вселенной P = 0 , потому что плотность энергии вещества будет больше, чем давление излучения, и вещество не движется с релятивистской скоростью.

Итак, уравнение жидкости станет,

$$\ dot {\ rho} = -3 \ left (\ frac {\ dot {a}} {a} \ right) \ rho$$

$$\ Rightarrow \ dot {\ rho} a + 3 \ dot {a} \ rho = 0$$

$$\ Rightarrow \ frac {1} {a ^ 3} \ frac {\ mathrm {d}} {\ mathrm {d} t} (a ^ 3 \ rho) = 0$$

 Rightarrow rhoa3=постоянная $$\ Rightarrow \ rho a ^ 3 = \: постоянная$$

$$\ Rightarrow \ rho \ propto \ frac {1} {a ^ 3}$$

В этом уравнении нет противоположной интуиции, потому что плотность должна масштабироваться как $a ^ {- 3}$, потому что объем увеличивается как $a ^ 3$.

Из последнего отношения мы можем сказать, что

$$\ frac {\ rho (t)} {\ rho_0} = \ left [\ frac {a_0} {a (t)} \ right] ^ 3$$

Для существующей вселенной а , равное _0, должно быть 1. Итак,

$$\ rho (t) = \ frac {\ rho_0} {a ^ 3}$$

В плоской вселенной с доминированием материи, k = 0. Таким образом, уравнение Фридмана станет

$$\ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3}$$

$$\ dot {a} ^ 2 = \ frac {8 \ pi G \ rho a ^ 2} {3}$$

Решив это уравнение, мы получим,

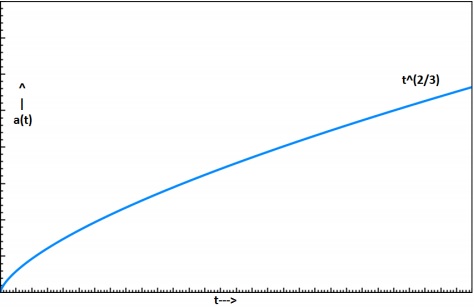
$$a \ propto t ^ {2/3}$$

$$\ frac {a (t)} {a_0} = \ left (\ frac {t} {t_0} \ right) ^ {2/3}$$

$$a (t) = \ left (\ frac {t} {t_0} \ right) ^ {2/3}$$

Это означает, что вселенная будет продолжать расти с уменьшающейся скоростью. На следующем изображении показано расширение пыльной вселенной.

Как ρ меняется со временем?

Взгляните на следующее уравнение —

$$\ frac {\ rho (t)} {\ rho_0} = \ left (\ frac {t_0} {t} \ right) ^ 2$$

Мы знаем, что масштабный коэффициент изменяется со временем как $t ^ {2/3}$. Так,

$$a (t) = \ left (\ frac {t} {t_0} \ right) ^ {2/3}$$

Различая это, мы получим,

$$\ frac {(da)} {dt} = \ dot {a} = \ frac {2} {3} \ left (\ frac {t ^ {- 1/3}} {t_0} \ right)$$

Мы знаем, что постоянная Хаббла

$$H (t) = \ frac {\ dot {a}} {a} = \ frac {2} {3t}$$

Это уравнение для Вселенной Эйнштейна-де Ситтера . Если мы хотим вычислить нынешний возраст вселенной, тогда

$$t_0 = t_ {age} = \ frac {2} {3H_0}$$

После присвоения значения $H_0$ для существующей вселенной мы получим значение возраста вселенной в 9 Гир . В нашей галактике Млечный путь есть много шаровых скоплений, которые имеют возрасты больше этого.

Это было все о пыльной вселенной. Теперь, если вы предполагаете, что во Вселенной преобладает излучение, а не материя, тогда плотность энергии излучения выражается как $a ^ {- 4}$, а не как $a ^ {- 3}$. Мы еще увидим это в следующей главе.

В космологии все происходит как частицы пыли, поэтому мы называем это пыльной вселенной или материальной вселенной.

Если мы предположим, что во вселенной преобладает излучение, а не материя, тогда плотность энергии излучения будет выражаться как $a ^ {- 4}$, а не как $a ^ {- 3}$.