Выпуклая оптимизация — минимумы и максимумы

 barx inS$\ bar {x} \ in \: S$ называется локальным минимумом функции $f$, если $f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right)$, где $N_ \ varepsilon \ left (\ bar {x} \ right)$ означает окрестность $\ bar {x}$, т. е. $N_ \ varepsilon \ left (\ bar {x} \ right)$ означает $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $

Локальные максимумы или максимизаторы

 barx inS$\ bar {x} \ in \: S$ называется локальным максимумом функции $f$, если $f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right)$, где $N_ \ varepsilon \ left (\ bar {x} \ right)$ означает окрестность $\ bar {x}$, т. е. $N_ \ varepsilon \ left (\ bar {x} \ right)$ означает $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $

Глобальные минимумы

 barx inS$\ bar {x} \ in \: S$ называется глобальным минимумом функции $f$, если $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ по всей сумме

Глобальные максимумы

 barx inS$\ bar {x} \ in \: S$ называется глобальным максимумом функции $f$, если $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ по всей сумме

Примеры

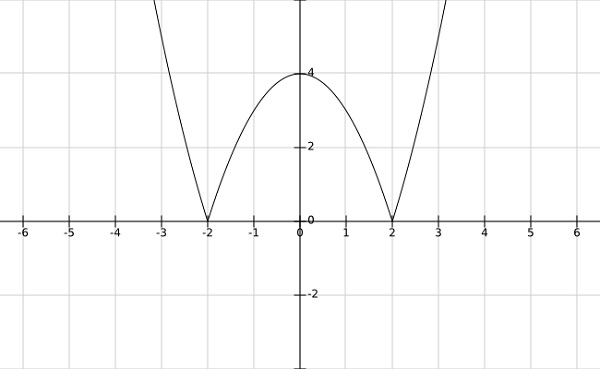
Шаг 1 — найдите локальные минимумы и максимумы $ f \ left (\ bar {x} \ right) = \ left | x ^ 2-4 \ right | $

Решение —

Из графика приведенной выше функции ясно, что локальные минимумы возникают при $x = \ pm 2$, а локальные максимумы — при $x = 0$.

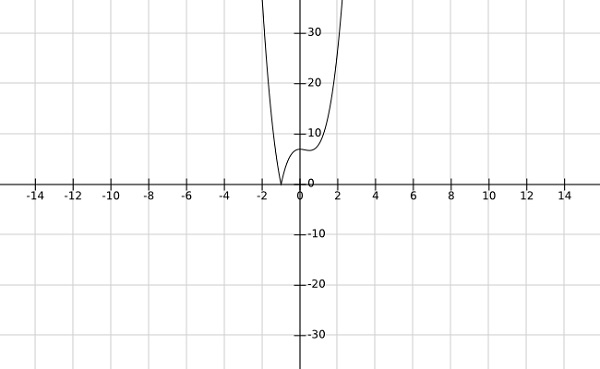
Шаг 2 — найти глобальные минимумы функции $ f \ left (x \ right) = \ left | 4x ^ 3-3x ^ 2 + 7 \ right | $

Решение —

Из графика приведенной выше функции видно, что глобальные минимумы возникают при $x = -1$.