Выпуклая оптимизация — Введение

Этот курс полезен для студентов, которые хотят решать задачи нелинейной оптимизации, возникающие в различных инженерных и научных приложениях. Этот курс начинается с базовой теории линейного программирования и вводит понятия выпуклых множеств и функций и связанных с ними терминологий для объяснения различных теорем, необходимых для решения задач нелинейного программирования. Этот курс представит различные алгоритмы, которые используются для решения таких проблем. Проблемы такого типа возникают в различных приложениях, включая машинное обучение, задачи оптимизации в электротехнике и т. Д. Это требует от учащихся предварительных знаний математических понятий и исчисления в старших классах.

В этом курсе студенты научатся решать задачи оптимизации, такие как $min f \ left (x \ right)$, с учетом некоторых ограничений.

Эти проблемы легко разрешимы, если функция $f \ left (x \ right)$ является линейной функцией и если ограничения линейны. Тогда это называется задачей линейного программирования (LPP). Но если ограничения являются нелинейными, то трудно решить вышеуказанную проблему. Если мы не можем построить функции на графике, то попытаться проанализировать оптимизацию можно одним способом, но мы не можем построить функцию, если она выходит за пределы трех измерений. Отсюда и методы нелинейного или выпуклого программирования для решения таких задач. В этом уроке мы сосредоточимся на изучении таких техник и, в конце концов, на нескольких алгоритмах для решения таких проблем. Сначала мы приведем понятие выпуклых множеств, которое является основой задач выпуклого программирования. Затем с введением выпуклых функций нам понадобятся некоторые важные теоремы для решения этих задач и некоторые алгоритмы, основанные на этих теоремах.

терминологической

• Пространство $\ mathbb {R} ^ n$ — это n-мерный вектор с действительными числами, определяемыми следующим образом — $\ mathbb {R} ^ n = \ left \ {\ left (x_1, x_2, ... , x_n \ right) ^ {\ tau}: x_1, x_2, ...., x_n \ in \ mathbb {R} \ right \}$

• Пространство $\ mathbb {R} ^ {mXn}$ — это множество матриц всех вещественных значений порядка $mXn$.

Пространство $\ mathbb {R} ^ n$ — это n-мерный вектор с действительными числами, определяемыми следующим образом — $\ mathbb {R} ^ n = \ left \ {\ left (x_1, x_2, ... , x_n \ right) ^ {\ tau}: x_1, x_2, ...., x_n \ in \ mathbb {R} \ right \}$

Пространство $\ mathbb {R} ^ {mXn}$ — это множество матриц всех вещественных значений порядка $mXn$.

Выпуклая оптимизация — линейное программирование

методология

Линейное программирование, также называемое линейной оптимизацией, — это метод, который используется для решения математических задач, в которых отношения являются линейными по природе. основная природа линейного программирования заключается в максимизации или минимизации целевой функции с учетом некоторых ограничений . Целевая функция — это линейная функция, полученная из математической модели задачи. Ограничения — это условия, которые накладываются на модель и также являются линейными.

• Из заданного вопроса найдите целевую функцию.
• найти ограничения.
• Нарисуйте ограничения на графике.
• найти допустимую область, которая образована пересечением всех ограничений.
• найти вершины допустимой области.
• найти значение целевой функции в этих вершинах.
• Вершина, которая либо максимизирует, либо минимизирует целевую функцию (в зависимости от вопроса) является ответом.

Примеры

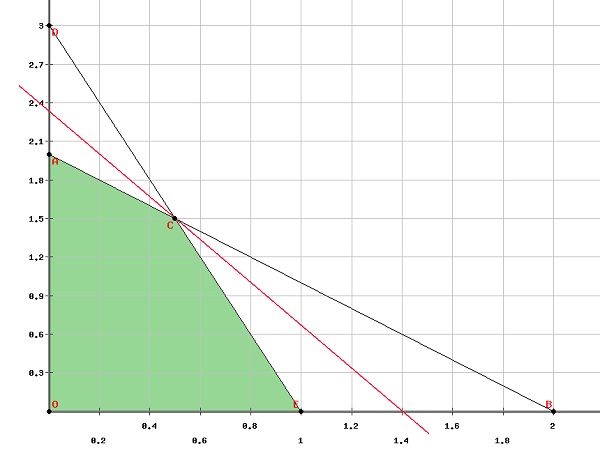
Шаг 1 — Максимизируйте $5x + 3y$ с учетом

$x + y \ leq 2$,

$3x + y \ leq 3$,

x geq0andy geq0$x \ geq 0 \: and \: y \ geq 0$

Решение —

Первый шаг — найти допустимую область на графике.

Из графика видно, что вершины допустимой области

$\ left (0, 0 \ right) \ left (0, 2 \ right) \ left (1, 0 \ right) \ left (\ frac {1} {2}, \ frac {3} {2} \ right )$

Пусть $f \ left (x, y \ right) = 5x + 3y$

Поместив эти значения в целевую функцию, мы получим —

$f \ left (0, 0 \ right)$ = 0

$f \ left (0, 2 \ right)$ = 6

$f \ left (1, 0 \ right)$ = 5

$f \ left (\ frac {1} {2}, \ frac {3} {2} \ right)$ = 7

Следовательно, функция максимизируется в $\ left (\ frac {1} {2}, \ frac {3} {2} \ right)$

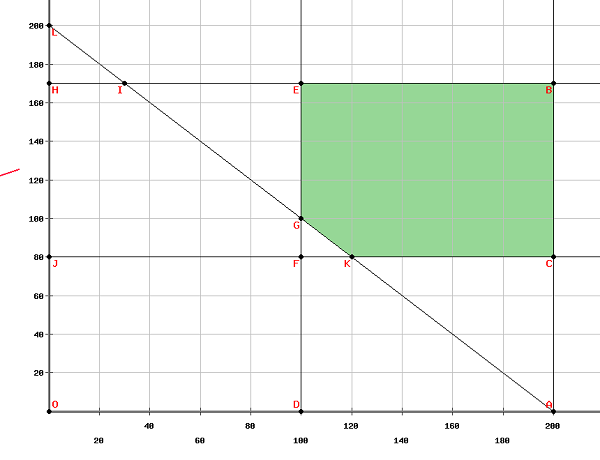
Шаг 2 — Часовая компания производит цифровые и механические часы. Долгосрочные прогнозы указывают на ожидаемый спрос не менее 100 цифровых и 80 механических часов каждый день. Из-за ограничений на производственную мощность в день можно производить не более 200 цифровых и 170 механических часов. Чтобы удовлетворить контракт на перевозку, каждый день отправляется не менее 200 часов.

Если каждая проданная цифровая модель приносит убыток в размере $\ $ 2 $, но каждая механическая модель приносит прибыль в размере$ \ $5$, сколько единиц каждого типа следует делать ежедневно, чтобы максимизировать чистую прибыль?

Решение —

Пусть $x$ будет количеством произведенных цифровых часов

$y$ — количество произведенных механических часов

В соответствии с этим вопросом, по крайней мере, 100 цифровых часов должны изготавливаться ежедневно, и может быть сделано максимум 200 цифровых часов.

 Rightarrow100 leqx leq200$\ Rightarrow 100 \ leq \: x \ leq 200$

Точно так же, по крайней мере, 80 механических часов должны изготавливаться ежедневно и максимум 170 механических часов.

 Rightarrow80 leqy leq170$\ Rightarrow 80 \ leq \: y \ leq 170$

Поскольку по крайней мере 200 часов должны выпускаться каждый день.

$\ Rightarrow x + y \ leq 200$

Поскольку каждая проданная цифровая модель приносит убыток в размере $\ $ 2 $, но каждая механическая модель приносит прибыль в размере$ \ $5$,

Общая прибыль может быть рассчитана как

$Прибыль = -2x + 5y$

И мы должны максимизировать прибыль, поэтому вопрос можно сформулировать так:

Увеличить $-2x + 5y$ при условии

100 leqx leq200$100 \: \ leq x \: \ leq 200$

80 leqy leq170$80 \: \ leq y \: \ leq 170$

x+y leq200$x + y \: \ leq 200$

Построив вышеприведенные уравнения на графике, получим,

Вершины допустимой области

$\ left (100, 170 \ right) \ left (200, 170 \ right) \ left (200, 180 \ right) \ left (120, 80 \ right) и \ left (100, 100 \ right)$

Максимальное значение целевой функции получается при $\ left (100, 170 \ right)$. Таким образом, чтобы максимизировать чистую прибыль, необходимо произвести 100 единиц цифровых часов и 170 единиц механических часов.

Выпуклая оптимизация — норма

Норма — это функция, которая дает строго положительное значение для вектора или переменной.

Норма — это функция $f: \ mathbb {R} ^ n \ rightarrow \ mathbb {R}$

Основными характеристиками нормы являются —

Пусть $X$ — такой вектор, что $X \ in \ mathbb {R} ^ n$

• $ \ left \ | x \ right \ | \ geq 0 $

• $ \ left \ | x \ right \ | = 0 \ Leftrightarrow x = 0 \ forall x \ in X $

• $ \ left \ | \ alpha x \ right \ | = \ left | \ alpha \ right | \ left \ | x \ right \ | \ forall \: x \ in X и \: \ alpha \: is \: a \: scalar $

• $ \ left \ | x + y \ right \ | \ leq \ left \ | x \ right \ | + \ left \ | y \ right \ | \ forall x, y \ in X $

• $ \ left \ | xy \ right \ | \ geq \ left \ | \ левый \ | x \ right \ | — \ left \ | y \ right \ | \ right \ | $

$ \ left \ | x \ right \ | \ geq 0 $

$ \ left \ | x \ right \ | = 0 \ Leftrightarrow x = 0 \ forall x \ in X $

$ \ left \ | \ alpha x \ right \ | = \ left | \ alpha \ right | \ left \ | x \ right \ | \ forall \: x \ in X и \: \ alpha \: is \: a \: scalar $

$ \ left \ | x + y \ right \ | \ leq \ left \ | x \ right \ | + \ left \ | y \ right \ | \ forall x, y \ in X $

$ \ left \ | xy \ right \ | \ geq \ left \ | \ левый \ | x \ right \ | — \ left \ | y \ right \ | \ right \ | $

По определению норма рассчитывается следующим образом —

• $ \ left \ | x \ right \ | _1 = \ displaystyle \ sum \ limit_ {i = 1} ^ n \ left | x_i \ right | $

• $ \ left \ | x \ right \ | _2 = \ left (\ displaystyle \ sum \ limit_ {i = 1} ^ n \ left | x_i \ right | ^ 2 \ right) ^ {\ frac {1} {2}} $

• $ \ left \ | x \ right \ | _p = \ left (\ displaystyle \ sum \ limit_ {i = 1} ^ n \ left | x_i \ right | ^ p \ right) ^ {\ frac {1} {p}}, 1 \ leq p \ leq \ infty $

$ \ left \ | x \ right \ | _1 = \ displaystyle \ sum \ limit_ {i = 1} ^ n \ left | x_i \ right | $

$ \ left \ | x \ right \ | _2 = \ left (\ displaystyle \ sum \ limit_ {i = 1} ^ n \ left | x_i \ right | ^ 2 \ right) ^ {\ frac {1} {2}} $

$ \ left \ | x \ right \ | _p = \ left (\ displaystyle \ sum \ limit_ {i = 1} ^ n \ left | x_i \ right | ^ p \ right) ^ {\ frac {1} {p}}, 1 \ leq p \ leq \ infty $

Норма — это непрерывная функция.

доказательство

По определению, если $x_n \ rightarrow x$ в $X \ Rightarrow f \ left (x_n \ right) \ rightarrow f \ left (x \ right)$, то $f \ left (x \ right)$ является постоянной функцией.

Пусть $ f \ left (x \ right) = \ left \ | x \ right \ | $

Следовательно, $ \ left | f \ left (x_n \ right) -f \ left (x \ right) \ right | = \ left | \ левый \ | x_n \ right \ | — \ слева \ | x \ right \ | \ right | \ leq \ left | \ левый | x_n-x \ right | \: \ right | $

Так как $x_n \ rightarrow x$, $ \ left \ | x_n-x \ right \ | \ rightarrow 0 $

Поэтому $ \ left | f \ left (x_n \ right) -f \ left (x \ right) \ right | \ leq 0 \ Rightarrow \ left | f \ left (x_n \ right) -f \ left (x \ right) \ right | = 0 \ Rightarrow f \ left (x_n \ right) \ rightarrow f \ left (x \ right) $

Следовательно, норма является непрерывной функцией.

Выпуклая оптимизация — внутренний продукт

Внутреннее произведение — это функция, которая дает скаляр для пары векторов.

Внутренний продукт — $f: \ mathbb {R} ^ n \ times \ mathbb {R} ^ n \ rightarrow \ kappa$, где $\ kappa$ — скаляр.

Основные характеристики внутреннего продукта следующие:

Пусть $X \ in \ mathbb {R} ^ n$

• $\ left \ langle x, x \ right \ rangle \ geq 0, \ forall x \ in X$

• $\ left \ langle x, x \ right \ rangle = 0 \ Leftrightarrow x = 0, \ forall x \ in X$

•  left langle alphax,y right rangle= alpha left langlex,y right rangle, forall alpha in kappaи forallx,y inX$\ left \ langle \ alpha x, y \ right \ rangle = \ alpha \ left \ langle x, y \ right \ rangle, \ forall \ alpha \ in \ kappa \: и \: \ forall x, y \ in X$

• $\ left \ langle x + y, z \ right \ rangle = \ left \ langle x, z \ right \ rangle + \ left \ langle y, z \ right \ rangle, \ forall x, y, z \ in X$

• $\ left \ langle \ overline {y, x} \ right \ rangle = \ left (x, y \ right), \ forall x, y \ in X$

$\ left \ langle x, x \ right \ rangle \ geq 0, \ forall x \ in X$

$\ left \ langle x, x \ right \ rangle = 0 \ Leftrightarrow x = 0, \ forall x \ in X$

 left langle alphax,y right rangle= alpha left langlex,y right rangle, forall alpha in kappaи forallx,y inX$\ left \ langle \ alpha x, y \ right \ rangle = \ alpha \ left \ langle x, y \ right \ rangle, \ forall \ alpha \ in \ kappa \: и \: \ forall x, y \ in X$

$\ left \ langle x + y, z \ right \ rangle = \ left \ langle x, z \ right \ rangle + \ left \ langle y, z \ right \ rangle, \ forall x, y, z \ in X$

$\ left \ langle \ overline {y, x} \ right \ rangle = \ left (x, y \ right), \ forall x, y \ in X$

Примечание —

• Связь между нормой и внутренним произведением: $ \ left \ | x \ right \ | = \ sqrt {\ left (x, x \ right)} $

• $\ forall x, y \ in \ mathbb {R} ^ n, \ left \ langle x, y \ right \ rangle = x_1y_1 + x_2y_2 + ... + x_ny_n$

Связь между нормой и внутренним произведением: $ \ left \ | x \ right \ | = \ sqrt {\ left (x, x \ right)} $

$\ forall x, y \ in \ mathbb {R} ^ n, \ left \ langle x, y \ right \ rangle = x_1y_1 + x_2y_2 + ... + x_ny_n$

Примеры

1. найти внутреннее произведение x= left(1,2,1 right)andy= left(3,−1,3 right)$x = \ left (1,2,1 \ right) \: and \: y = \ left (3, -1,3 \ right)$

Решение

$\ left \ langle x, y \ right \ rangle = x_1y_1 + x_2y_2 + x_3y_3$

$\ left \ langle x, y \ right \ rangle = \ left (1 \ times3 \ right) + \ left (2 \ times-1 \ right) + \ left (1 \ times3 \ right)$

$\ left \ langle x, y \ right \ rangle = 3 + \ left (-2 \ right) + 3$

$\ left \ langle x, y \ right \ rangle = 4$

2. Если $x = \ left (4,9,1 \ right), y = \ left (-3,5,1 \ right)$ и $z = \ left (2,4,1 \ right)$, найти $\ left (x + y, z \ right)$

Решение

Как мы знаем, $\ left \ langle x + y, z \ right \ rangle = \ left \ langle x, z \ right \ rangle + \ left \ langle y, z \ right \ rangle$

$\ left \ langle x + y, z \ right \ rangle = \ left (x_1z_1 + x_2z_2 + x_3z_3 \ right) + \ left (y_1z_1 + y_2z_2 + y_3z_3 \ right)$

$\ left \ langle x + y, z \ right \ rangle = \ left \ {\ left (4 \ times 2 \ right) + \ left (9 \ times 4 \ right) + \ left (1 \ times1 \ right) \ right \} +$

$\ left \ {\ left (-3 \ times2 \ right) + \ left (5 \ times4 \ right) + \ left (1 \ times 1 \ right) \ right \}$

$\ left \ langle x + y, z \ right \ rangle = \ left (8 + 36 + 1 \ right) + \ left (-6 + 20 + 1 \ right)$

$\ left \ langle x + y, z \ right \ rangle = 45 + 15$

$\ left \ langle x + y, z \ right \ rangle = 60$

Выпуклая оптимизация — минимумы и максимумы

Местные минимумы или минимизировать

 barx inS$\ bar {x} \ in \: S$ называется локальным минимумом функции $f$, если $f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right)$, где $N_ \ varepsilon \ left (\ bar {x} \ right)$ означает окрестность $\ bar {x}$, т. е. $N_ \ varepsilon \ left (\ bar {x} \ right)$ означает $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $

Локальные максимумы или максимизаторы

 barx inS$\ bar {x} \ in \: S$ называется локальным максимумом функции $f$, если $f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right)$, где $N_ \ varepsilon \ left (\ bar {x} \ right)$ означает окрестность $\ bar {x}$, т. е. $N_ \ varepsilon \ left (\ bar {x} \ right)$ означает $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $

Глобальные минимумы

 barx inS$\ bar {x} \ in \: S$ называется глобальным минимумом функции $f$, если $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ по всей сумме

Глобальные максимумы

 barx inS$\ bar {x} \ in \: S$ называется глобальным максимумом функции $f$, если $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ по всей сумме

Примеры

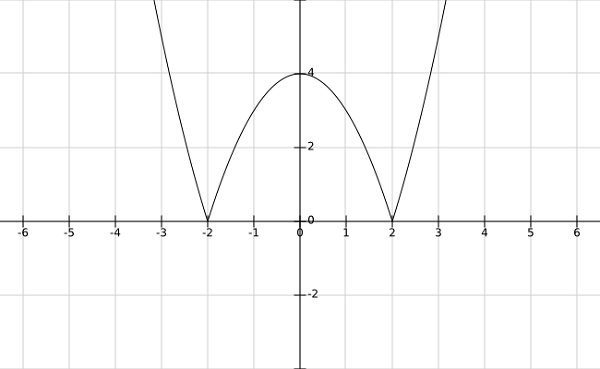
Шаг 1 — найдите локальные минимумы и максимумы $ f \ left (\ bar {x} \ right) = \ left | x ^ 2-4 \ right | $

Решение —

Из графика приведенной выше функции ясно, что локальные минимумы возникают при $x = \ pm 2$, а локальные максимумы — при $x = 0$.

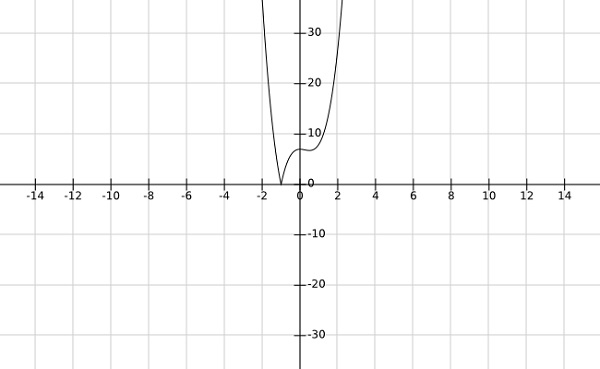
Шаг 2 — найти глобальные минимумы функции $ f \ left (x \ right) = \ left | 4x ^ 3-3x ^ 2 + 7 \ right | $

Решение —

Из графика приведенной выше функции видно, что глобальные минимумы возникают при $x = -1$.

Выпуклая оптимизация — выпуклый набор

Пусть $S \ subseteq \ mathbb {R} ^ n$. Множество S называется выпуклым, если отрезок, соединяющий любые две точки множества S, также принадлежит S, т. Е. Если $x_1, x_2 \ in S$ , тогда $\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ in S$, где $\ lambda \ in \ left (0,1 \ right)$.

Примечание —

• Объединение двух выпуклых множеств может быть или не быть выпуклым.
• Пересечение двух выпуклых множеств всегда выпукло.

доказательство

Пусть $S_1$ и $S_2$ — два выпуклых множества.

Пусть $S_3 = S_1 \ cap S_2$

Пусть $x_1, x_2 \ in S_3$

Так как $S_3 = S_1 \ cap S_2$, таким образом, $x_1, x_2 \ in S_1$ и $x_1, x_2 \ in S_2$

Поскольку $S_i$ является выпуклым множеством, $\ forall$ $i \ in 1,2,$

Таким образом, $\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ in S_i$, где $\ lambda \ in \ left (0,1 \ right)$

Поэтому $\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ in S_1 \ cap S_2$

$\ Rightarrow \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ in S_3$

Следовательно, $S_3$ является выпуклым множеством.

• Средневзвешенное значение в форме $\ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i$, где $\ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_i = 1$ и $\ lambda_i \ geq 0 , \ forall i \ in \ left [1, k \ right]$ называется конической комбинацией $x_1, x_2, .... x_k.$

• Средневзвешенное значение вида $\ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i$, где $\ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_i = 1$ называется аффинной комбинацией $x_1 , x_2, .... x_k.$

• Средневзвешенное значение вида $\ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i$ называется линейной комбинацией $x_1, x_2, .... x_k.$

Средневзвешенное значение в форме $\ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i$, где $\ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_i = 1$ и $\ lambda_i \ geq 0 , \ forall i \ in \ left [1, k \ right]$ называется конической комбинацией $x_1, x_2, .... x_k.$

Средневзвешенное значение вида $\ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i$, где $\ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_i = 1$ называется аффинной комбинацией $x_1 , x_2, .... x_k.$

Средневзвешенное значение вида $\ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i$ называется линейной комбинацией $x_1, x_2, .... x_k.$

Примеры

Шаг 1 — Докажите, что множество $S = \ left \ {x \ in \ mathbb {R} ^ n: Cx \ leq \ alpha \ right \}$ является выпуклым множеством.

Решение

Пусть $x_1$ и $x_2 \ in S$

$\ Rightarrow Cx_1 \ leq \ alpha$ и $\: and \: Cx_2 \ leq \ alpha$

Показать: $\: \: y = \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ in S \: \ forall \: \ lambda \ in \ left (0,1 \ верно)$

$Cy = C \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) = \ lambda Cx_1 + \ left (1- \ lambda \ right) Cx_2$

$\ Rightarrow Cy \ leq \ lambda \ alpha + \ left (1- \ lambda \ right) \ alpha$

$\ Rightarrow Cy \ leq \ alpha$

$\ Rightarrow y \ in S$

Следовательно, $S$ является выпуклым множеством.

Шаг 2 — Докажите, что множество $S = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_ {1} ^ {2} \ leq 8x_2 \ right \}$ равно выпуклое множество.

Решение

Пусть $x, y \ in S$

Пусть $x = \ left (x_1, x_2 \ right)$ и $y = \ left (y_1, y_2 \ right)$

$\ Rightarrow x_ {1} ^ {2} \ leq 8x_2$ и $y_ {1} ^ {2} \ leq 8y_2$

Чтобы показать — $\ lambda x + \ left (1- \ lambda \ right) y \ in S \ Rightarrow \ lambda \ left (x_1, x_2 \ right) + \ left (1- \ lambda \ right) \ left (y_1, y_2 \ right) \ in S \ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda) y_2] \ in S \ right) \ right]$

$Теперь \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} = \ lambda ^ 2x_ {1} ^ {2} + \ left (1- \ lambda \ right) ^ 2y_ {1} ^ {2} +2 \ lambda \ left (1- \ lambda \ right) x_1y_1$

Но $2x_1y_1 \ leq x_ {1} ^ {2} + y_ {1} ^ {2}$

Следовательно,

$\ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} \ leq \ lambda ^ 2x_ {1} ^ {2} + \ left (1- \ lambda \ right) ^ 2y_ {1} ^ {2} +2 \ lambda \ left (1- \ lambda \ right) \ left (x_ {1} ^ {2} + y_ {1} ^ {2} \ right)$

$\ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} \ leq \ lambda x_ {1} ^ {2} + \ left (1- \ lambda \ right) y_ {1} ^ {2}$

$\ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} \ leq 8 \ lambda x_2 + 8 \ left (1- \ lambda \ right) y_2$

$\ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} \ leq 8 \ left [\ lambda x_2 + \ left (1- \ lambda \ right) y_2 \ right]$

$\ Rightarrow \ lambda x + \ left (1- \ lambda \ right) y \ in S$

Шаг 3 — Показать, что множество $S \ in \ mathbb {R} ^ n$ является выпуклым тогда и только тогда, когда для каждого целого числа k каждая выпуклая комбинация любых k точек из $S$ находится в $S$.

Решение

Пусть $S$ — выпуклое множество. затем, чтобы показать;

$c_1x_1 + c_2x_2 + ..... + c_kx_k \ in S, \ displaystyle \ sum \ limit_ {1} ^ k c_i = 1, c_i \ geq 0, \ forall i \ in 1,2, ...., k$

Доказательство по индукции

Для $k = 1, x_1 \ in S, c_1 = 1 \ Rightarrow c_1x_1 \ in S$

Для $k = 2, x_1, x_2 \ in S, c_1 + c_2 = 1$ и поскольку S — выпуклое множество

$\ Rightarrow c_1x_1 + c_2x_2 \ in S.$

Пусть выпуклая комбинация m точек S находится в S, т. Е.

$c_1x_1 + c_2x_2 + ... + c_mx_m \ in S, \ displaystyle \ sum \ limit_ {1} ^ m c_i = 1, c_i \ geq 0, \ forall i \ in 1,2, ..., m$

Теперь пусть $x_1, x_2 ...., x_m, x_ {m + 1} \ in S$

Пусть $x = \ mu_1x_1 + \ mu_2x_2 + ... + \ mu_mx_m + \ mu_ {m + 1} x_ {m + 1}$

Пусть $x = \ left (\ mu_1 + \ mu_2 + ... + \ mu_m \ right) \ frac {\ mu_1x_1 + \ mu_2x_2 + \ mu_mx_m} {\ mu_1 + \ mu_2 + ......... + \ mu_m} + \ mu_ {т + 1} X_ {т + 1}$

Пусть $y = \ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_mx_m} {\ mu_1 + \ mu_2 + ......... + \ mu_m}$

$\ Rightarrow x = \ left (\ mu_1 + \ mu_2 + ... + \ mu_m \ right) y + \ mu_ {m + 1} x_ {m + 1}$

Теперь $y \ in S$, потому что сумма коэффициентов равна 1.

$\ Rightarrow x \ in S$, поскольку S — выпуклое множество и $y, x_ {m + 1} \ in S$

Следовательно, доказано по индукции.

Выпуклая оптимизация — аффинный набор

Множество $A$ называется аффинным множеством, если для любых двух различных точек прямая, проходящая через эти точки, лежит в множестве $A$.

Примечание —

• $S$ является аффинным множеством тогда и только тогда, когда оно содержит каждую аффинную комбинацию своих точек.

• Пустые и одноэлементные множества являются аффинными и выпуклыми множествами.

  Например, решение линейного уравнения является аффинным множеством.

$S$ является аффинным множеством тогда и только тогда, когда оно содержит каждую аффинную комбинацию своих точек.

Пустые и одноэлементные множества являются аффинными и выпуклыми множествами.

Например, решение линейного уравнения является аффинным множеством.

доказательство

Пусть S — решение линейного уравнения.

По определению $S = \ left \ {x \ in \ mathbb {R} ^ n: Ax = b \ right \}$

Пусть $x_1, x_2 \ in S \ Rightarrow Ax_1 = b$ и $Ax_2 = b$

Для доказательства: $A \ left [\ theta x_1 + \ left (1- \ theta \ right) x_2 \ right] = b, \ forall \ theta \ in \ left (0,1 \ right)$

$A \ left [\ theta x_1 + \ left (1- \ theta \ right) x_2 \ right] = \ theta Ax_1 + \ left (1- \ theta \ right) Ax_2 = \ theta b + \ left (1- \ theta \ right) ) B = B$

Таким образом, S является аффинным множеством.

теорема

Если $C$ является аффинным множеством и $x_0 \ in C$, то множество $V = C-x_0 = \ left \ {x-x_0: x \ in C \ right \}$ является подпространством в C.

доказательство

Пусть $x_1, x_2 \ in V$

Показать: $\ alpha x_1 + \ beta x_2 \ in V$ для некоторого $\ alpha, \ beta$

Теперь $x_1 + x_0 \ in C$ и $x_2 + x_0 \ in C$ по определению V

Теперь $\ alpha x_1 + \ beta x_2 + x_0 = \ alpha \ left (x_1 + x_0 \ right) + \ beta \ left (x_2 + x_0 \ right) + \ left (1- \ alpha - \ beta \ right) x_0$

Но $\ alpha \ left (x_1 + x_0 \ right) + \ beta \ left (x_2 + x_0 \ right) + \ left (1- \ alpha - \ beta \ right) x_0 \ in C$, потому что C является аффинным множеством ,

Следовательно, $\ alpha x_1 + \ beta x_2 \ in V$

Отсюда доказано.

Выпуклая оптимизация — корпус

Выпуклая оболочка множества точек в S является границей наименьшей выпуклой области, которая содержит все точки S внутри или на ее границе.

ИЛИ ЖЕ

Пусть $S \ subseteq \ mathbb {R} ^ n$ Выпуклая оболочка S, обозначаемая как $Co \ left (S \ right)$ by, является совокупностью всех выпуклых комбинаций S, т. Е. $X \ in Co \ left. (S \ right)$ тогда и только тогда, когда $x \ in \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_ix_i$, где $\ displaystyle \ sum \ limit_ {1} ^ n \ lambda_i = 1$ и $\ lambda_i \ geq 0 \ forall x_i \ in S$

Замечание. Оболочка множества точек в S на плоскости определяет выпуклый многоугольник, а точки S на границе многоугольника определяют вершины многоугольника.

Теорема $Co \ left (S \ right) = \ left \ {x: x = \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_ix_i, x_i \ in S, \ displaystyle \ sum \ limit_ {i = 1 } ^ n \ lambda_i = 1, \ lambda_i \ geq 0 \ right \}$ Показать, что выпуклая оболочка является выпуклым множеством.

доказательство

Пусть $x_1, x_2 \ in Co \ left (S \ right)$, затем $x_1 = \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_ix_i$ и $x_2 = \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_ \ gamma x_i$, где $\ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_i = 1, \ lambda_i \ geq 0$ и $\ displaystyle \ sum \ limit_ {i = 1} ^ n \ gamma_i = 1, \ gamma_i \ geq0$

Для $\ theta \ in \ left (0,1 \ right), \ theta x_1 + \ left (1- \ theta \ right) x_2 = \ theta \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_ix_i + \ left (1- \ theta \ right) \ displaystyle \ sum \ limit_ {i = 1} ^ n \ gamma_ix_i$

$\ theta x_1 + \ left (1- \ theta \ right) x_2 = \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_i \ theta x_i + \ displaystyle \ sum \ limit_ {i = 1} ^ n \ gamma_i \ слева (1- \ theta \ right) x_i$

$\ theta x_1 + \ left (1- \ theta \ right) x_2 = \ displaystyle \ sum \ limit_ {i = 1} ^ n \ left [\ lambda_i \ theta + \ gamma_i \ left (1- \ theta \ right) \ правильно] x_i$

Учитывая коэффициенты,

$\ displaystyle \ sum \ limit_ {i = 1} ^ n \ left [\ lambda_i \ theta + \ gamma_i \ left (1- \ theta \ right) \ right] = \ theta \ displaystyle \ sum \ limit_ {i = 1 } ^ n \ lambda_i + \ left (1- \ theta \ right) \ displaystyle \ sum \ limit_ {i = 1} ^ n \ gamma_i = \ theta + \ left (1- \ theta \ right) = 1$

Следовательно, $\ theta x_1 + \ left (1- \ theta \ right) x_2 \ in Co \ left (S \ right)$

Таким образом, выпуклая оболочка является выпуклым множеством.

Теорема Каратеодори

Пусть S — произвольное множество в $\ mathbb {R} ^ n$. Если $x \ in Co \ left (S \ right)$, то $x \ in Co \ left (x_1, x_2, ...., x_n, x_ {n + 1} \ right)$.

доказательство

Так как $x \ in Co \ left (S \ right)$, то $x$ представляется выпуклой комбинацией конечного числа точек в S, т. Е.

$x = \ displaystyle \ sum \ limit_ {j = 1} ^ k \ lambda_jx_j, \ displaystyle \ sum \ limit_ {j = 1} ^ k \ lambda_j = 1, \ lambda_j \ geq 0$ и $x_j \ in S, \ forall j \ in \ left (1, k \ right)$

Если $k \ leq n + 1$, полученный результат, очевидно, верен.

Если $k \ geq n + 1$, то $\ left (x_2-x_1 \ right) \ left (x_3-x_1 \ right), ....., \ left (x_k-x_1 \ right)$ линейно зависимы ,

$\ Rightarrow \ существует \ mu _j \ in \ mathbb {R}, 2 \ leq j \ leq k$ (не все ноль), так что $\ displaystyle \ sum \ limit_ {j = 2} ^ k \ mu _j \ left (x_j-x_1 \ right) = 0$

Определите $\ mu_1 = - \ displaystyle \ sum \ limit_ {j = 2} ^ k \ mu _j$, затем $\ displaystyle \ sum \ limit_ {j = 1} ^ k \ mu_j x_j = 0, \ displaystyle \ sum \ limit_ {j = 1} ^ k \ mu_j = 0$

где не все $\ mu_j's$ равны нулю. Так как $\ displaystyle \ sum \ limit_ {j = 1} ^ k \ mu_j = 0$, по крайней мере один из $\ mu_j&amp;gt; 0,1 \ leq j \ leq k$

Тогда $x = \ displaystyle \ sum \ limit_ {1} ^ k \ lambda_j x_j + 0$

$x = \ displaystyle \ sum \ limit_ {1} ^ k \ lambda_j x_j- \ alpha \ displaystyle \ sum \ limit_ {1} ^ k \ mu_j x_j$

$x = \ displaystyle \ sum \ limit_ {1} ^ k \ left (\ lambda_j- \ alpha \ mu_j \ right) x_j$

Выберите $\ alpha$ так, чтобы $\ alpha = min \ left \ {\ frac {\ lambda_j} {\ mu_j}, \ mu_j \ geq 0 \ right \} = \ frac {\ lambda_j} {\ mu _j},$ для некоторых $i = 1,2, ..., k$

Если $\ mu_j \ leq 0, \ lambda_j- \ alpha \ mu_j \ geq 0$

Если $\ mu_j&amp;gt; 0, то \: \ frac {\ lambda _j} {\ mu_j} \ geq \ frac {\ lambda_i} {\ mu _i} = \ alpha \ Rightarrow \ lambda_j- \ alpha \ mu_j \ geq 0, J = 1,2, ... к$

В частности, $\ lambda_i- \ alpha \ mu_i = 0$ по определению $\ alpha$

$x = \ displaystyle \ sum \ limit_ {j = 1} ^ k \ left (\ lambda_j- \ alpha \ mu_j \ right) x_j$, где

$\ lambda_j- \ alpha \ mu_j \ geq0$ и $\ displaystyle \ sum \ limit_ {j = 1} ^ k \ left (\ lambda_j- \ alpha \ mu_j \ right) = 1$ и $\ lambda_i- \ alpha \ mu_i = 0$

Таким образом, x можно представить в виде выпуклой комбинации не более (k-1) точек.

Этот процесс восстановления может повторяться до тех пор, пока x не будет представлен как выпуклая комбинация (n + 1) элементов.

Выпуклая оптимизация — теорема Вейерштрасса

Пусть S — непустое, замкнутое и ограниченное множество (также называемое компактным множеством) в $\ mathbb {R} ^ n$, и пусть $f: S \ rightarrow \ mathbb {R}$ — непрерывная функция на S, тогда задача min $\ left \ {f \ left (x \ right): x \ in S \ right \}$ достигает своего минимума.

доказательство

Поскольку S непусто и ограничено, существует нижняя граница.

$\ alpha = Inf \ left \ {f \ left (x \ right): x \ in S \ right \}$

Теперь пусть $S_j = \ left \ {x \ in S: \ alpha \ leq f \ left (x \ right) \ leq \ alpha + \ delta ^ j \ right \} \ forall j = 1,2, ...$ и $\ delta \ in \ left (0,1 \ right)$

По определению инфимия $S_j$ непусто для каждого $j$.

Выберите $x_j \ in S_j$, чтобы получить последовательность $\ left \ {x_j \ right \}$ для $j = 1,2, ...$

Поскольку S ограничена, последовательность также ограничена и существует сходящаяся подпоследовательность $\ left \ {y_j \ right \}$, которая сходится к $\ hat {x}$. Следовательно, $\ hat {x}$ является предельной точкой, и S замкнута, поэтому $\ hat {x} \ in S$. Поскольку f непрерывна, $f \ left (y_i \ right) \ rightarrow f \ left (\ hat {x} \ right)$.

Так как $\ alpha \ leq f \ left (y_i \ right) \ leq \ alpha + \ delta ^ k, \ alpha = \ displaystyle \ lim_ {k \ rightarrow \ infty} f \ left (y_i \ right) = f \ left ( \ hat {x} \ right)$

Таким образом, $\ hat {x}$ является минимизирующим решением.

замечания

Для выполнения теоремы Вейерштрасса есть два важных необходимых условия. Это следующие —

• Шаг 1 — Множество S должно быть ограниченным множеством.

  Рассмотрим функцию f \ left (x \ right) = x $.

  Это неограниченное множество, и оно имеет минимумы в любой точке своей области.

  Таким образом, для получения минимумов S должен быть ограничен.

• Шаг 2 — Набор S должен быть закрыт.

  Рассмотрим функцию $f \ left (x \ right) = \ frac {1} {x}$ в области \ left (0,1 \ right).

  Эта функция не является замкнутой в данной области и ее минимумов также не существует.

  Следовательно, для получения минимумов S следует замкнуть.

Шаг 1 — Множество S должно быть ограниченным множеством.

Рассмотрим функцию f \ left (x \ right) = x $.

Это неограниченное множество, и оно имеет минимумы в любой точке своей области.

Таким образом, для получения минимумов S должен быть ограничен.

Шаг 2 — Набор S должен быть закрыт.

Рассмотрим функцию $f \ left (x \ right) = \ frac {1} {x}$ в области \ left (0,1 \ right).

Эта функция не является замкнутой в данной области и ее минимумов также не существует.

Следовательно, для получения минимумов S следует замкнуть.

Выпуклая оптимизация — теорема о ближайшей точке

Пусть S — непустое замкнутое выпуклое множество в $\ mathbb {R} ^ n$, и пусть $y \ notin S$, тогда $\ существует$ точка $\ bar {x} \ in S$ с минимальным расстоянием от у, т. е. $ \ left \ | y- \ bar {x} \ right \ | \ leq \ left \ | yx \ right \ | \ forall x \ in S. $

Кроме того, $\ bar {x}$ является минимизирующей точкой тогда и только тогда, когда $\ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq 0$ или $\ left (y- \ hat {x}, x- \ hat {x} \ right) \ leq 0$

доказательство

Наличие ближайшей точки

Поскольку $S \ ne \ phi, \ существует$ точка $\ hat {x} \ in S$, такая, что минимальное расстояние S от y меньше или равно $ \ left \ | y- \ hat {x} \ right \ | $.

Определите $ \ hat {S} = S \ cap \ left \ {x: \ left \ | yx \ right \ | \ leq \ left \ | y- \ hat {x} \ right \ | \ right \} $

Поскольку $\ hat {S}$ замкнуто и ограничено, а норма является непрерывной функцией, то по теореме Вейерштрасса существует минимальная точка $\ hat {x} \ в S$ такая, что $ \ left \ | y- \ hat {x} \ right \ | = Inf \ left \ {\ left \ | yx \ right \ |, x \ in S \ right \} $

уникальность

Предположим, что $\ bar {x} \ in S$ такой, что $ \ left \ | y- \ hat {x} \ right \ | = \ left \ | y- \ hat {x} \ right \ | = \ alpha $

Поскольку S выпуклая, $\ frac {\ hat {x} + \ bar {x}} {2} \ in S$

Но, $ \ left \ | y- \ frac {\ hat {x} — \ bar {x}} {2} \ right \ | \ leq \ frac {1} {2} \ left \ | y- \ hat {x} \ right \ | + \ frac {1} {2} \ left \ | y- \ bar {x} \ right \ | = \ alpha $

Это не может быть строгим неравенством, потому что $\ hat {x}$ ближе всего к y.

Следовательно, $ \ left \ | y- \ hat {x} \ right \ | = \ mu \ left \ | y- \ hat {x} \ right \ | $, для некоторых$ \ mu $

Теперь $ \ left \ | \ mu \ right \ | = 1. $Если$ \ mu = -1 $, то$ \ left (y- \ hat {x} \ right) = — \ left (y- \ hat {x} \ right) \ Правая стрелка y = \ frac {\ hat {x} + \ bar {x}} {2} \ in S $

Но $y \ in S$. Отсюда и противоречие. Таким образом, $\ mu = 1 \ Rightarrow \ hat {x} = \ bar {x}$

Таким образом, точка минимизации уникальна.

Во второй части доказательства предположим, что $\ left (y- \ hat {x} \ right) ^ {\ tau} \ left (x- \ bar {x} \ right) \ leq 0$ для всех $x \ в S$

Сейчас,

$ \ left \ | yx \ right \ | ^ {2} = \ left \ | y- \ hat {x} + \ hat {x} -x \ right \ | ^ {2} = \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ left \ | \ hat {x} -x \ right \ | ^ {2} +2 \ left (\ hat {x} -x \ right) ^ {\ tau} \ left (y- \ hat {x} \ right) $

$ \ Rightarrow \ left \ | yx \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ {2} $, потому что$ \ left \ | \ hat {x} -x \ right \ | ^ {2} \ geq 0 $и$ \ left (\ hat {x} — x \ right) ^ {T} \ left (y- \ hat {x} \ right ) \ geq 0 $

Таким образом, $\ hat {x}$ является минимизирующей точкой.

И наоборот, предположим, что $\ hat {x}$ является минимизируемой точкой.

$ \ Rightarrow \ left \ | yx \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ 2 \ forall x \ in S $

Так как S выпуклое множество.

$\ Rightarrow \ lambda x + \ left (1- \ lambda \ right) \ hat {x} = \ hat {x} + \ lambda \ left (x- \ hat {x} \ right) \ in S$ для $x \ in S$ и $\ lambda \ in \ left (0,1 \ right)$

Теперь $ \ left \ | y- \ hat {x} — \ lambda \ left (x- \ hat {x} \ right) \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ 2 $

А также

$ \ left \ | y- \ hat {x} — \ lambda \ left (x- \ hat {x} \ right) \ right \ | ^ {2} = \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ lambda ^ 2 \ left \ | x- \ hat {x} \ right \ | ^ {2} -2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) $

$ \ Rightarrow \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ lambda ^ {2} \ left \ | x- \ hat {x} \ right \ | -2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ geq \ left \ | y- \ hat {x} \ right \ | ^ {2} $

$ \ Rightarrow 2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq \ lambda ^ 2 \ left \ | x- \ hat {x} \ right \ | ^ 2 $

$\ Rightarrow \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq 0$

Отсюда доказано.

Теорема о фундаментальном разделении

Пусть S — непустое замкнутое выпуклое множество в $\ mathbb {R} ^ n$ и $y \ notin S$. Тогда существует ненулевой вектор $p$ и скалярный $\ beta$ такой, что $p ^ T y&amp;gt; \ beta$ и $p ^ T x &amp;lt;\ beta$ для каждого $x \ in S$

доказательство

Поскольку S — непустое замкнутое выпуклое множество и $y \ notin S$, то по теореме о ближайшей точке существует единственная минимизирующая точка $\ hat {x} \ in S$, такая что

$\ left (x- \ hat {x} \ right) ^ T \ left (y- \ hat {x} \ right) \ leq 0 \ forall x \ in S$

Пусть $p = \ left (y- \ hat {x} \ right) \ neq 0$ и $\ beta = \ hat {x} ^ T \ left (y- \ hat {x} \ right) = p ^ T \ шляпа {х}$.

Тогда $\ left (x- \ hat {x} \ right) ^ T \ left (y- \ hat {x} \ right) \ leq 0$

$\ Rightarrow \ left (y- \ hat {x} \ right) ^ T \ left (x- \ hat {x} \ right) \ leq 0$

$\ Rightarrow \ left (y- \ hat {x} \ right) ^ Tx \ leq \ left (y- \ hat {x} \ right) ^ T \ hat {x} = \ hat {x} ^ T \ left (y- \ hat {x} \ right)$ i, т.е. $p ^ Tx \ leq \ beta$

Кроме того, $p ^ Ty- \ beta = \ left (y- \ hat {x} \ right) ^ Ty- \ hat {x} ^ T \ left (y- \ hat {x} \ right)$

$ = \ left (y- \ hat {x} \ right) ^ T \ left (yx \ right) = \ left \ | y- \ hat {x} \ right \ | ^ {2}> 0 $

$\ Rightarrow p ^ Ty&amp;gt; \ beta$

Эта теорема приводит к разделению гиперплоскостей. Гиперплоскости, основанные на приведенной выше теореме, могут быть определены следующим образом:

Пусть $S_1$ и $S_2$ — непустые подмножества в $\ mathbb {R}$, а $H = \ left \ {X: A ^ TX = b \ right \}$ — гиперплоскость.

• Говорят, что гиперплоскость H разделяет $S_1$ и $S_2$, если $A ^ TX \ leq b \ forall X \ in S_1$ и $A_TX \ geq b \ forall X \ in S_2$

• Говорят, что гиперплоскость H строго разделяет $S_1$ и $S_2$, если $A ^ TX &amp;lt;b \ forall X \ in S_1$ и $A_TX&amp;gt; b \ forall X \ in S_2$

• Говорят, что гиперплоскость H сильно разделяет $S_1$ и $S_2$, если $A ^ TX \ leq b \ forall X \ in S_1$ и $A_TX \ geq b + \ varepsilon \ forall X \ in S_2$, где $\ varepsilon$ — это положительный скаляр.

Говорят, что гиперплоскость H разделяет $S_1$ и $S_2$, если $A ^ TX \ leq b \ forall X \ in S_1$ и $A_TX \ geq b \ forall X \ in S_2$

Говорят, что гиперплоскость H строго разделяет $S_1$ и $S_2$, если $A ^ TX &amp;lt;b \ forall X \ in S_1$ и $A_TX&amp;gt; b \ forall X \ in S_2$

Говорят, что гиперплоскость H сильно разделяет $S_1$ и $S_2$, если $A ^ TX \ leq b \ forall X \ in S_1$ и $A_TX \ geq b + \ varepsilon \ forall X \ in S_2$, где $\ varepsilon$ — это положительный скаляр.

Выпуклая оптимизация — конусы

Говорят, что непустое множество C в $\ mathbb {R} ^ n$ конусно с вершиной 0, если $x \ in C \ Rightarrow \ lambda x \ in C \ forall \ lambda \ geq 0$.

Множество C является выпуклым конусом, если он выпуклый так же, как и конус.

Например, $ y = \ left | x \ right | $ не является выпуклым конусом, потому что он не выпуклый.

Но $ y \ geq \ left | x \ right | $ — выпуклый конус, потому что он выпуклый и конус.

Примечание . Конус C является выпуклым тогда и только тогда, когда для любого $x, y \ in C, x + y \ in C$.

доказательство

Поскольку C — конус, для $x, y \ in C \ Rightarrow \ lambda x \ in C$ и $\ mu y \ in C \: \ forall \: \ lambda, \ mu \ geq 0$

C является выпуклым, если $\ lambda x + \ left (1- \ lambda \ right) y \ in C \: \ forall \: \ lambda \ in \ left (0, 1 \ right)$

Поскольку C — конус, $\ lambda x \ in C$ и $\ left (1- \ lambda \ right) y \ in C \ Leftrightarrow x, y \ in C$

Таким образом, C является выпуклым, если $x + y \ in C$

В общем, если $x_1, x_2 \ in C$, то $\ lambda_1x_1 + \ lambda_2x_2 \ in C, \ forall \ lambda_1, \ lambda_2 \ geq 0$

Примеры

• Коническая комбинация бесконечного множества векторов в $\ mathbb {R} ^ n$ является выпуклым конусом.

• Любое пустое множество является выпуклым конусом.

• Любая линейная функция является выпуклым конусом.

• Поскольку гиперплоскость линейна, она также является выпуклым конусом.

• Замкнутые полупространства также являются выпуклыми конусами.

Коническая комбинация бесконечного множества векторов в $\ mathbb {R} ^ n$ является выпуклым конусом.

Любое пустое множество является выпуклым конусом.

Любая линейная функция является выпуклым конусом.

Поскольку гиперплоскость линейна, она также является выпуклым конусом.

Замкнутые полупространства также являются выпуклыми конусами.

Примечание . Пересечение двух выпуклых конусов является выпуклым конусом, но их объединение может быть или не быть выпуклым конусом.

Выпуклая оптимизация — полярный конус

Пусть S — непустое множество в $\ mathbb {R} ^ n$. Тогда полярный конус S, обозначаемый $S ^ *$, задается через $S ^ * = \ left \ {p \ in \ mathbb {R } ^ n, p ^ Tx \ leq 0 \: \ forall x \ in S \ right \}$.

замечание

• Полярный конус всегда выпуклый, даже если S не выпуклый.

• Если S пустое множество, $S ^ * = \ mathbb {R} ^ n$.

• Полярность можно рассматривать как обобщение ортогональности.

Полярный конус всегда выпуклый, даже если S не выпуклый.

Если S пустое множество, $S ^ * = \ mathbb {R} ^ n$.

Полярность можно рассматривать как обобщение ортогональности.

Пусть $C \ subseteq \ mathbb {R} ^ n$, то ортогональное пространство C, обозначаемое $C ^ \ perp = \ left \ {y \ in \ mathbb {R} ^ n: \ left \ langle x, y \ right \ rangle = 0 \ forall x \ in C \ right \}$.

лемма

Пусть $S, S_1$ и $S_2$ — непустые множества в $\ mathbb {R} ^ n$, тогда следующие утверждения верны:

• $S ^ *$ — замкнутый выпуклый конус.

• $S \ subseteq S ^ {**}$ где $S ^ {**}$ — полярный конус $S ^ *$.

• $S_1 \ subseteq S_2 \ Rightarrow S_ {2} ^ {*} \ subseteq S_ {1} ^ {*}$.

$S ^ *$ — замкнутый выпуклый конус.

$S \ subseteq S ^ {**}$ где $S ^ {**}$ — полярный конус $S ^ *$.

$S_1 \ subseteq S_2 \ Rightarrow S_ {2} ^ {*} \ subseteq S_ {1} ^ {*}$.

доказательство

Шаг 1 — $S ^ * = \ left \ {p \ in \ mathbb {R} ^ n, p ^ Tx \ leq 0 \: \ forall \: x \ in S \ right \}$

• Пусть $x_1, x_2 \ in S ^ * \ Rightarrow x_ {1} ^ {T} x \ leq 0$ и $x_ {2} ^ {T} x \ leq 0, \ forall x \ in S$

  Для $\ lambda \ in \ left (0, 1 \ right), \ left [\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right] ^ Tx = \ left [\ left (\ lambda x_1 \ right) ) ^ T + \ left \ {\ left (1- \ lambda \ right) x_ {2} \ right \} ^ {T} \ right] x, \ forall x \ in S$

  $= \ left [\ lambda x_ {1} ^ {T} + \ left (1- \ lambda \ right) x_ {2} ^ {T} \ right] x = \ lambda x_ {1} ^ {T} x + \ left (1- \ lambda \ right) x_ {2} ^ {T} \ leq 0$

  Таким образом, $\ lambda x_1 + \ left (1- \ lambda \ right) x_ {2} \ in S ^ *$

  Следовательно, $S ^ *$ — выпуклое множество.

• Для $\ lambda \ geq 0, p ^ {T} x \ leq 0, \ forall \: x \ in S$

  Следовательно, $\ lambda p ^ T x \ leq 0,$

  $\ Rightarrow \ left (\ lambda p \ right) ^ T x \ leq 0$

  $\ Rightarrow \ lambda p \ in S ^ *$

  Таким образом, $S ^ *$ является конусом.

• Показывать, что $S ^ *$ замкнуто, т. Е. Показывать, что если $p_n \ rightarrow p$ как $n \ rightarrow \ infty$, то $p \ in S ^ *$

  $\ forall x \ in S, p_ {n} ^ {T} xp ^ T x = \ left (p_n-p \ right) ^ T x$

  As $p_n \ rightarrow p$ as $n \ rightarrow \ infty \ Rightarrow \ left (p_n \ rightarrow p \ right) \ rightarrow 0$

  Следовательно, $p_ {n} ^ {T} x \ rightarrow p ^ {T} x$. Но $p_ {n} ^ {T} x \ leq 0, \: \ forall x \ in S$

  Таким образом, $p ^ Tx \ leq 0, \ forall x \ in S$

  $\ Rightarrow p \ in S ^ *$

  Следовательно, $S ^ *$ замкнуто.

Пусть $x_1, x_2 \ in S ^ * \ Rightarrow x_ {1} ^ {T} x \ leq 0$ и $x_ {2} ^ {T} x \ leq 0, \ forall x \ in S$

Для $\ lambda \ in \ left (0, 1 \ right), \ left [\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right] ^ Tx = \ left [\ left (\ lambda x_1 \ right) ) ^ T + \ left \ {\ left (1- \ lambda \ right) x_ {2} \ right \} ^ {T} \ right] x, \ forall x \ in S$

$= \ left [\ lambda x_ {1} ^ {T} + \ left (1- \ lambda \ right) x_ {2} ^ {T} \ right] x = \ lambda x_ {1} ^ {T} x + \ left (1- \ lambda \ right) x_ {2} ^ {T} \ leq 0$

Таким образом, $\ lambda x_1 + \ left (1- \ lambda \ right) x_ {2} \ in S ^ *$

Следовательно, $S ^ *$ — выпуклое множество.

Для $\ lambda \ geq 0, p ^ {T} x \ leq 0, \ forall \: x \ in S$

Следовательно, $\ lambda p ^ T x \ leq 0,$

$\ Rightarrow \ left (\ lambda p \ right) ^ T x \ leq 0$

$\ Rightarrow \ lambda p \ in S ^ *$

Таким образом, $S ^ *$ является конусом.

Показывать, что $S ^ *$ замкнуто, т. Е. Показывать, что если $p_n \ rightarrow p$ как $n \ rightarrow \ infty$, то $p \ in S ^ *$

$\ forall x \ in S, p_ {n} ^ {T} xp ^ T x = \ left (p_n-p \ right) ^ T x$

As $p_n \ rightarrow p$ as $n \ rightarrow \ infty \ Rightarrow \ left (p_n \ rightarrow p \ right) \ rightarrow 0$

Следовательно, $p_ {n} ^ {T} x \ rightarrow p ^ {T} x$. Но $p_ {n} ^ {T} x \ leq 0, \: \ forall x \ in S$

Таким образом, $p ^ Tx \ leq 0, \ forall x \ in S$

$\ Rightarrow p \ in S ^ *$

Следовательно, $S ^ *$ замкнуто.

Шаг 2 — $S ^ {**} = \ left \ {q \ in \ mathbb {R} ^ n: q ^ T p \ leq 0, \ forall p \ in S ^ * \ right \}$

Пусть $x \ in S$, затем $\ forall p \ in S ^ *, p ^ T x \ leq 0 \ Rightarrow x ^ Tp \ leq 0 \ Rightarrow x \ in S ^ {**}$

Таким образом, $S \ subseteq S ^ {**}$

Шаг 3 — $S_2 ^ * = \ left \ {p \ in \ mathbb {R} ^ n: p ^ Tx \ leq 0, \ forall x \ in S_2 \ right \}$

Так как $S_1 \ subseteq S_2 \ Rightarrow \ forall x \ in S_2 \ Rightarrow \ forall x \ in S_1$

Следовательно, если $\ hat {p} \ in S_2 ^ *,$, то $\ hat {p} ^ Tx \ leq 0, \ forall x \ in S_2$

$\ Rightarrow \ hat {p} ^ Tx \ leq 0, \ forall x \ in S_1$

$\ Rightarrow \ hat {p} ^ T \ in S_1 ^ *$

$\ Rightarrow S_2 ^ * \ subseteq S_1 ^ *$

теорема

Пусть C — непустой замкнутый выпуклый конус, тогда $C = C ^ **$

доказательство

$C = C ^ {**}$ по предыдущей лемме.

Для доказательства: $x \ in C ^ {**} \ subseteq C$

Пусть $x \ in C ^ {**}$ и пусть $x \ notin C$

Тогда по фундаментальной теореме разделения существует вектор $p \ neq 0$ и скалярный $\ alpha$ такой, что $p ^ Ty \ leq \ alpha, \ forall y \ in C$

Следовательно, $p ^ Tx&amp;gt; \ alpha$

Но, поскольку $\ left (y = 0 \ right) \ in C$ и $p ^ Ty \ leq \ alpha, \ forall y \ in C \ Rightarrow \ alpha \ geq 0$ и $p ^ Tx&amp;gt; 0$

Если $p \ notin C ^ *$, то существует некоторый $\ bar {y} \ in C$ такой, что $p ^ T \ bar {y}&amp;gt; 0$ и $p ^ T \ left (\ lambda \ bar {y} \ right)$ можно сделать сколь угодно большим, если взять $\ lambda$ достаточно большим.

Это противоречит тому факту, что $p ^ Ty \ leq \ alpha, \ forall y \ in C$

Следовательно, $p \ in C ^ *$

Поскольку $x \ in C ^ * = \ left \ {q: q ^ Tp \ leq 0, \ forall p \ in C ^ * \ right \}$

Следовательно, $x ^ Tp \ leq 0 \ Rightarrow p ^ Tx \ leq 0$

Но $p ^ Tx&amp;gt; \ alpha$

Такова контракция.

Таким образом, $x \ in C$

Следовательно, $C = C ^ {**}$.

Выпуклая оптимизация — коническая комбинация

Точка вида $\ alpha_1x_1 + \ alpha_2x_2 + .... + \ alpha_nx_n$ с $\ alpha_1, \ alpha_2, ..., \ alpha_n \ geq 0$ называется конической комбинацией $x_1, x_2, ..., x_n.$

• Если $x_i$ находится в выпуклом конусе C, то любая коническая комбинация $x_i$ также находится в C.

• Множество C является выпуклым конусом, если оно содержит все конические комбинации своих элементов.

Если $x_i$ находится в выпуклом конусе C, то любая коническая комбинация $x_i$ также находится в C.

Множество C является выпуклым конусом, если оно содержит все конические комбинации своих элементов.

Коническая оболочка

Коническая оболочка определяется как набор всех конических комбинаций данного набора S и обозначается как coni (S).

Таким образом, $coni \ left (S \ right) = \ left \ {\ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i: x_i \ in S, \ lambda_i \ in \ mathbb {R}, \ lambda_i \ geq 0, i = 1,2, ... \ right \}$

• Коническая оболочка является выпуклым множеством.
• Происхождение всегда принадлежит коническому корпусу.

Выпуклая оптимизация — многогранный набор

Множество в $\ mathbb {R} ^ n$ называется многогранным, если оно является пересечением конечного числа замкнутых полупространств, т. Е.

$S = \ left \ {x \ in \ mathbb {R} ^ n: p_ {i} ^ {T} x \ leq \ alpha_i, i = 1,2, ...., n \ right \}$

Например,

• $\ left \ {x \ in \ mathbb {R} ^ n: AX = b \ right \}$

• $\ left \ {x \ in \ mathbb {R} ^ n: AX \ leq b \ right \}$

• $\ left \ {x \ in \ mathbb {R} ^ n: AX \ geq b \ right \}$

$\ left \ {x \ in \ mathbb {R} ^ n: AX = b \ right \}$

$\ left \ {x \ in \ mathbb {R} ^ n: AX \ leq b \ right \}$

$\ left \ {x \ in \ mathbb {R} ^ n: AX \ geq b \ right \}$

Многогранный конус

Множество в $\ mathbb {R} ^ n$ называется многогранным конусом, если оно является пересечением конечного числа полупространств, содержащих начало координат, т. Е. $S = \ left \ {x \ in \ mathbb { R} ^ n: p_ {i} ^ {T} x \ leq 0, i = 1, 2, ... \ right \}$

многогранник

Многогранник — это многогранное множество, ограниченное.

замечания

• Многогранник — это выпуклая оболочка конечного множества точек.
• Многогранный конус порожден конечным набором векторов.
• Многогранное множество является замкнутым множеством.
• Многогранное множество является выпуклым множеством.

Крайняя точка выпуклого множества

Пусть S — выпуклое множество в $\ mathbb {R} ^ n$. Вектор $x \ in S$ называется крайней точкой S, если $x = \ lambda x_1 + \ left (1- \ lambda \ right) x_2$ с $x_1, x_2 \ in S$ и $\ lambda \ in \ left (0, 1 \ right) \ Rightarrow x = x_1 = x_2$.

пример

Шаг 1 — $S = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 1 \ право \}$

Крайняя точка, $E = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_ {1} ^ {2} + x_ {2} ^ {2} = 1 \ right \}$

Шаг 2 — $S = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_1 + x_2 &amp;lt;2, -x_1 + 2x_2 \ leq 2, x_1, x_2 \ geq 0 \ право \}$

Крайняя точка, $E = \ left \ {\ left (0, 0 \ right), \ left (2, 0 \ right), \ left (0, 1 \ right), \ left (\ frac {2} {3 }, \ frac {4} {3} \ right) \ right \}$

Шаг 3 — S — многогранник, составленный из точек $\ left \ {\ left (0,0 \ right), \ left (1,1 \ right), \ left (1,3 \ right), \ left (- 2,4 \ направо), \ налево (0,2 \ направо) \ направо \}$

Крайняя точка, $E = \ left \ {\ left (0,0 \ right), \ left (1,1 \ right), \ left (1,3 \ right), \ left (-2,4 \ right) \ right \}$

замечания

• Любая точка выпуклого множества S, может быть представлена ​​как выпуклая комбинация его крайних точек.

• Это верно только для замкнутых и ограниченных множеств в $\ mathbb {R} ^ n$.

• Это может быть не так для неограниченных множеств.

Любая точка выпуклого множества S, может быть представлена ​​как выпуклая комбинация его крайних точек.

Это верно только для замкнутых и ограниченных множеств в $\ mathbb {R} ^ n$.

Это может быть не так для неограниченных множеств.

k крайних точек

Точка в выпуклом множестве называется k экстремальной тогда и только тогда, когда она является внутренней точкой k-мерного выпуклого множества в S и не является внутренней точкой (k + 1) -мерного выпуклого множества в S. В принципе, для выпуклого множества S k крайних точек образуют k-мерные открытые грани.

Выпуклая оптимизация — направление

Пусть S — замкнутое выпуклое множество в $\ mathbb {R} ^ n$. Ненулевой вектор $d \ in \ mathbb {R} ^ n$ называется направлением S, если для каждого $x \ in S, x + \ lambda d \ in S, \ forall \ lambda \ geq 0.$

• Два направления $d_1$ и $d_2$ в S называются различными, если $d \ neq \ alpha d_2$ для $\ alpha&amp;gt; 0$.

• Направление $d$ в $S$ называется крайним направлением, если его нельзя записать в виде положительной линейной комбинации двух разных направлений, т. Е. Если $d = \ lambda _1d_1 + \ lambda _2d_2$ для $\ lambda _1, \ лямбда _2&amp;gt; 0$, затем $d_1 = \ alpha d_2$ для некоторого $\ alpha$.

• Любое другое направление может быть выражено как положительная комбинация экстремальных направлений.

• Для выпуклого множества $S$ направление d такое, что $x + \ lambda d \ in S$ для некоторого $x \ in S$ и всех $\ lambda \ geq0$ называется рецессивным для $S$.

• Пусть E — множество точек, в которых некоторая функция $f: S \ rightarrow$ над непустым выпуклым множеством S в $\ mathbb {R} ^ n$ достигает своего максимума, тогда $E$ называется открытой гранью $S$. Направления открытых лиц называются открытыми направлениями.

• Луч, чье направление является экстремальным, называется экстремальным.

Два направления $d_1$ и $d_2$ в S называются различными, если $d \ neq \ alpha d_2$ для $\ alpha&amp;gt; 0$.

Направление $d$ в $S$ называется крайним направлением, если его нельзя записать в виде положительной линейной комбинации двух разных направлений, т. Е. Если $d = \ lambda _1d_1 + \ lambda _2d_2$ для $\ lambda _1, \ лямбда _2&amp;gt; 0$, затем $d_1 = \ alpha d_2$ для некоторого $\ alpha$.

Любое другое направление может быть выражено как положительная комбинация экстремальных направлений.

Для выпуклого множества $S$ направление d такое, что $x + \ lambda d \ in S$ для некоторого $x \ in S$ и всех $\ lambda \ geq0$ называется рецессивным для $S$.

Пусть E — множество точек, в которых некоторая функция $f: S \ rightarrow$ над непустым выпуклым множеством S в $\ mathbb {R} ^ n$ достигает своего максимума, тогда $E$ называется открытой гранью $S$. Направления открытых лиц называются открытыми направлениями.

Луч, чье направление является экстремальным, называется экстремальным.

пример

Рассмотрим функцию $f \ left (x \ right) = y = \ left | x \ right |$, где $x \ in \ mathbb {R} ^ n$. Пусть d будет единичным вектором в $\ mathbb {R} ^ n$

Тогда d является направлением для функции f, потому что для любого $\ lambda \ geq 0, x + \ lambda d \ in f \ left (x \ right)$.

Выпуклая и вогнутая функция

Пусть $f: S \ rightarrow \ mathbb {R}$, где S — непустое выпуклое множество в $\ mathbb {R} ^ n$, тогда $f \ left (x \ right)$ называется выпуклым на S если $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left ( x_2 \ right), \ forall \ lambda \ in \ left (0,1 \ right)$.

С другой стороны, пусть $f: S \ rightarrow \ mathbb {R}$, где S — непустое выпуклое множество в $\ mathbb {R} ^ n$, тогда говорят $f \ left (x \ right)$ быть вогнутым на S, если $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ geq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) ) f \ left (x_2 \ right), \ forall \ lambda \ in \ left (0, 1 \ right)$.

Пусть $f: S \ rightarrow \ mathbb {R}$, где S — непустое выпуклое множество в $\ mathbb {R} ^ n$, тогда $f \ left (x \ right)$ называется строго выпуклым на S если $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) &amp;lt;\ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right), \ forall \ lambda \ in \ left (0, 1 \ right)$.

Пусть $f: S \ rightarrow \ mathbb {R}$, где S — непустое выпуклое множество в $\ mathbb {R} ^ n$, тогда $f \ left (x \ right)$ называется строго вогнутым на S если $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right)&amp;gt; \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right), \ forall \ lambda \ in \ left (0, 1 \ right)$.

Примеры

• Линейная функция является выпуклой и вогнутой.

• $ f \ left (x \ right) = \ left | x \ right | $ — выпуклая функция.

• $f \ left (x \ right) = \ frac {1} {x}$ — выпуклая функция.

Линейная функция является выпуклой и вогнутой.

$ f \ left (x \ right) = \ left | x \ right | $ — выпуклая функция.

$f \ left (x \ right) = \ frac {1} {x}$ — выпуклая функция.

теорема

Пусть $f_1, f_2, ..., f_k: \ mathbb {R} ^ n \ rightarrow \ mathbb {R}$ — выпуклые функции. Рассмотрим функцию $f \ left (x \ right) = \ displaystyle \ sum \ limit_ {j = 1} ^ k \ alpha_jf_j \ left (x \ right)$, где $\ alpha_j&amp;gt; 0, j = 1, 2,. ..k,$ then $f \ left (x \ right)$ — выпуклая функция.

доказательство

Поскольку $f_1, f_2, ... f_k$ являются выпуклыми функциями

Следовательно, $f_i \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f_i \ left (x_1 \ right) + \ left (1- \ lambda \ right) f_i \ left (x_2 \ right), \ forall \ lambda \ in \ left (0, 1 \ right)$ и $i = 1, 2, ...., k$

Рассмотрим функцию $f \ left (x \ right)$.

Следовательно,

$f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right)$

$= \ displaystyle \ sum \ limit_ {j = 1} ^ k \ alpha_jf_j \ left (\ lambda x_1 + 1- \ lambda \ right) x_2 \ leq \ displaystyle \ sum \ limit_ {j = 1} ^ k \ alpha_j \ лямбда f_j \ left (x_1 \ right) + \ left (1- \ lambda \ right) f_j \ left (x_2 \ right)$

$\ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda \ left (\ displaystyle \ sum \ limit_ {j = 1} ^ k \ alpha _jf_j \ left ( x_1 \ right) \ right) + \ left (\ displaystyle \ sum \ limit_ {j = 1} ^ k \ alpha _jf_j \ left (x_2 \ right) \ right)$

$\ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_2 \ right) \ leq \ left (1- \ lambda \ right) f \ левый (x_2 \ правый)$

Следовательно, $f \ left (x \ right)$ — выпуклая функция.

теорема

Пусть $f \ left (x \ right)$ — выпуклая функция на выпуклом множестве $S \ subset \ mathbb {R} ^ n$, тогда локальные минимумы $f \ left (x \ right)$ на S — это глобальные минимумы.

доказательство

Пусть $\ hat {x}$ — локальные минимумы для $f \ left (x \ right)$, а $\ hat {x}$ — не глобальные минимумы.

следовательно, $\ существует \ hat {x} \ в S$ такое, что $f \ left (\ bar {x} \ right) &amp;lt;f \ left (\ hat {x} \ right)$

Поскольку $\ hat {x}$ является локальным минимумом, существует окрестность $N_ \ varepsilon \ left (\ hat {x} \ right)$, такая что $f \ left (\ hat {x} \ right) \ leq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ hat {x} \ right) \ cap S$

Но $f \ left (x \ right)$ — выпуклая функция на S, поэтому для $\ lambda \ in \ left (0, 1 \ right)$

у нас есть $\ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} \ leq \ lambda f \ left (\ hat {x} \ right) + \ left (1- \ lambda \ right) f \ left (\ bar {x} \ right)$

$\ Rightarrow \ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} &amp;lt;\ lambda f \ left (\ hat {x} \ right) + \ left (1- \ lambda \ справа) f \ left (\ hat {x} \ right)$

$\ Rightarrow \ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} &amp;lt;f \ left (\ hat {x} \ right), \ forall \ lambda \ in \ left (0 , 1 \ справа)$

Но для некоторого $\ lambda &amp;lt;1$, но близко к 1, мы имеем

$\ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} \ in N_ \ varepsilon \ left (\ hat {x} \ right) \ cap S$ и $f \ left ( \ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} \ right) &amp;lt;f \ left (\ bar {x} \ right)$

что противоречие.

Следовательно, $\ bar {x}$ является глобальным минимумом.

Эпиграф

пусть S — непустое подмножество в $\ mathbb {R} ^ n$, и пусть $f: S \ rightarrow \ mathbb {R}$, тогда эпиграф из f, обозначаемый epi (f) или $E_f$, является подмножеством $\ mathbb {R} ^ n + 1$, определяемый как $E_f = \ left \ {\ left (x, \ alpha \ right): x \ in \ mathbb {R} ^ n, \ alpha \ in \ mathbb { R}, f \ left (x \ right) \ leq \ alpha \ right \}$

подграфик

пусть S — непустое подмножество в $\ mathbb {R} ^ n$, и пусть $f: S \ rightarrow \ mathbb {R}$, тогда гипограф f обозначается через hyp (f) или $H_f = \ left \ {\ left (x, \ alpha \ right): x \ in \ mathbb {R} ^ n, \ alpha \ in \ mathbb {R} ^ n, \ alpha \ in \ mathbb {R}, f \ left ( x \ right) \ geq \ alpha \ right \}$

теорема

Пусть S — непустое выпуклое множество в $\ mathbb {R} ^ n$, и пусть $f: S \ rightarrow \ mathbb {R} ^ n$, тогда f является выпуклым тогда и только тогда, когда его эпиграф $E_f$ равен выпуклое множество.

доказательство

Пусть f — выпуклая функция.

Показать $E_f$ — выпуклое множество.

Пусть $\ left (x_1, \ alpha_1 \ right), \ left (x_2, \ alpha_2 \ right) \ in E_f, \ lambda \ in \ left (0, 1 \ right)$

Показать $\ lambda \ left (x_1, \ alpha_1 \ right) + \ left (1- \ lambda \ right) \ left (x_2, \ alpha_2 \ right) \ in E_f$

$\ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda \ right) x_2, \ lambda \ alpha_1 + \ left (1- \ lambda \ right) \ alpha_2 \ right] \ in E_f$

$f \ left (x_1 \ right) \ leq \ alpha _1, f \ left (x_2 \ right) \ leq \ alpha _2$

Следовательно, $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right)$

$\ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda \ alpha_1 + \ left (1- \ lambda \ right) \ alpha_2$

обратный

Пусть $E_f$ — выпуклое множество.

Чтобы показать, что f является выпуклым.

то есть, чтобы показать, если $x_1, x_2 \ in S, \ lambda \ left (0, 1 \ right)$

$f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ право)$

Пусть $x_1, x_2 \ in S, \ lambda \ in \ left (0, 1 \ right), f \ left (x_1 \ right), f \ left (x_2 \ right) \ in \ mathbb {R}$

Поскольку $E_f$ является выпуклым множеством, $\ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2, \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) \ справа) f \ left (x_2 \ right) \ in E_f$

Следовательно, $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right)$

Выпуклая оптимизация — неравенство Дженсена

Пусть S — непустое выпуклое множество в $\ mathbb {R} ^ n$ и $f: S \ rightarrow \ mathbb {R} ^ n$. Тогда f выпуклая тогда и только тогда, когда для каждого целого числа $k&amp;gt; 0$

$x_1, x_2, ... x_k \ in S, \ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_i = 1, \ lambda_i \ geq 0, \ forall i = 1,2, s, k$, у нас есть $f \ left (\ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i \ right) \ leq \ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda _if \ left (x \ right)$

доказательство

По индукции на к.

$k = 1: x_1 \ in S$ Следовательно, $f \ left (\ lambda_1 x_1 \ right) \ leq \ lambda_i f \ left (x_1 \ right)$, потому что $\ lambda_i = 1$.

$k = 2: \ lambda_1 + \ lambda_2 = 1$ и $x_1, x_2 \ in S$

Следовательно, $\ lambda_1x_1 + \ lambda_2x_2 \ in S$

Следовательно, по определению, $f \ left (\ lambda_1 x_1 + \ lambda_2 x_2 \ right) \ leq \ lambda _1f \ left (x_1 \ right) + \ lambda _2f \ left (x_2 \ right)$

Пусть утверждение верно для $n &amp;lt;k$

Следовательно,

$f \ left (\ lambda_1 x_1 + \ lambda_2 x_2 + .... + \ lambda_k x_k \ right) \ leq \ lambda_1 f \ left (x_1 \ right) + \ lambda_2 f \ left (x_2 \ right) + ... + \ lambda_k f \ left (x_k \ right)$

$k = n + 1:$ Let $x_1, x_2, .... x_n, x_ {n + 1} \ in S$ и $\ displaystyle \ sum \ limit_ {i = 1} ^ {n + 1} = 1$

Поэтому $\ mu_1x_1 + \ mu_2x_2 + ....... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ in S$

таким образом, $f \ left (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right)$

$= f \ left (\ left (\ mu_1 + \ mu_2 + ... + \ mu_n \ right) \ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n} {\ mu_1 + \ mu_2 + \ mu_3} + \ mu_ {n + 1} x_ {n + 1} \ right)$

$= f \ left (\ mu_y + \ mu_ {n + 1} x_ {n + 1} \ right)$ где $\ mu = \ mu_1 + \ mu_2 + ... + \ mu_n$ и

$y = \ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n} {\ mu_1 + \ mu_2 + ... + \ mu_n}$, а также $\ mu_1 + \ mu_ {n + 1} = 1, y \ in S$

$\ Rightarrow f \ left (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right) \ leq \ mu f \ left (y \ right) + \ mu_ {n +1} f \ left (x_ {n + 1} \ right)$

$\ Rightarrow f \ left (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right) \ leq$

$\ left (\ mu_1 + \ mu_2 + ... + \ mu_n \ right) f \ left (\ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n} {\ mu_1 + \ mu_2 + ... + \ mu_n} \ right) + \ mu_ {n + 1} f \ left (x_ {n + 1} \ right)$

$\ Rightarrow f \ left (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right) \ leq \ left (\ mu_1 + \ mu_2 + ... + \ mu_n \ верно)$

$\ left [\ frac {\ mu_1} {\ mu_1 + \ mu_2 + ... + \ mu_n} f \ left (x_1 \ right) + ... + \ frac {\ mu_n} {\ mu_1 + \ mu_2 + ... + \ mu_n} f \ left (x_n \ right) \ right] + \ mu_ {n + 1} f \ left (x_ {n + 1} \ right)$

$\ Rightarrow f \ left (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right) \ leq \ mu_1f \ left (x_1 \ right) + \ mu_2f \ left ( x_2 \ right) + ....$

Отсюда доказано.

Выпуклая оптимизация — дифференцируемая функция

Пусть S — непустое открытое множество в $\ mathbb {R} ^ n$, тогда $f: S \ rightarrow \ mathbb {R}$ называется дифференцируемым в $\ hat {x} \ in S$, если существует вектор $\ bigtriangledown f \ left (\ hat {x} \ right)$, называемый вектором градиента, и функция $\ alpha: \ mathbb {R} ^ n \ rightarrow \ mathbb {R}$ такая, что

$ f \ left (x \ right) = f \ left (\ hat {x} \ right) + \ bigtriangledown f \ left (\ hat {x} \ right) ^ T \ left (x- \ hat {x} \ правый) + \ левый \ | x = \ hat {x} \ right \ | \ alpha \ left (\ hat {x}, x- \ hat {x} \ right), \ forall x \ in S $, где

$\ alpha \ left (\ hat {x}, x- \ hat {x} \ right) \ rightarrow 0 \ bigtriangledown f \ left (\ hat {x} \ right) = \ left [\ frac {\ частичный f} {\ частичный x_1} \ frac {\ частичный f} {\ частичный x_2} ... \ frac {\ частичный f} {\ частичный x_n} \ right] _ {x = \ hat {x}} ^ {T}$

теорема

пусть S — непустое открытое выпуклое множество в $\ mathbb {R} ^ n$, и пусть $f: S \ rightarrow \ mathbb {R}$ дифференцируемо на S. Тогда f выпукло тогда и только тогда, когда для $x_1, x_2 \ in S, \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) \ leq f \ left (x_1 \ right) -f \ left (x_2 \ right)$

доказательство

Пусть f — выпуклая функция. то есть для $x_1, x_2 \ in S, \ lambda \ in \ left (0, 1 \ right)$

$f \ left [\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right] \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ право)$

$\ Rightarrow f \ left [\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right] \ leq \ lambda \ left (f \ left (x_1 \ right) -f \ left (x_2 \ right) \ right ) + f \ left (x_2 \ right)$

$\ Rightarrow \ lambda \ left (f \ left (x_1 \ right) -f \ left (x_2 \ right) \ right) \ geq f \ left (x_2 + \ lambda \ left (x_1-x_2 \ right) \ right) - f \ left (x_2 \ right)$

$\ Rightarrow \ lambda \ left (f \ left (x_1 \ right) -f \ left (x_2 \ right) \ right) \ geq f \ left (x_2 \ right) + \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) \ лямбда +$

$ \ left \ | \ lambda \ left (x_1-x_2 \ right) \ right \ | \ alpha \ left (x_2, \ lambda \ left (x_1 — x_2 \ right) -f \ left (x_2 \ right) \ right) $

где $\ alpha \ left (x_2, \ lambda \ left (x_1 - x_2 \ right) \ right) \ rightarrow 0$ как $\ lambda \ rightarrow 0$

Разделив $\ lambda$ на обе стороны, получим —

$f \ left (x_1 \ right) -f \ left (x_2 \ right) \ geq \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right)$

обратный

Пусть для $x_1, x_2 \ in S, \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) \ leq f \ left (x_1 \ right) -f \ left (x_2 \ right)$

Чтобы показать, что f выпуклая.

Поскольку S выпуклый, $x_3 = \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ in S, \ lambda \ in \ left (0, 1 \ right)$

Так как $x_1, x_3 \ in S$, следовательно,

$f \ left (x_1 \ right) -f \ left (x_3 \ right) \ geq \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1 -x_3 \ right)$

$\ Rightarrow f \ left (x_1 \ right) -f \ left (x_3 \ right) \ geq \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1 - \ lambda x_1- \ left (1- \ lambda) \ right) x_2 \ right)$

$\ Rightarrow f \ left (x_1 \ right) -f \ left (x_3 \ right) \ geq \ left (1- \ lambda \ right) \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1 - x_2 \ право)$

Так как, $x_2, x_3 \ in S$, следовательно,

$f \ left (x_2 \ right) -f \ left (x_3 \ right) \ geq \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_2-x_3 \ right)$

$\ Rightarrow f \ left (x_2 \ right) -f \ left (x_3 \ right) \ geq \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_2- \ lambda x_1- \ left (1- \ lambda) \ right) x_2 \ right)$

$\ Rightarrow f \ left (x_2 \ right) -f \ left (x_3 \ right) \ geq \ left (- \ lambda \ right) \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1-x_2 \ верно)$

Таким образом, объединяя приведенные выше уравнения, получаем —

$\ lambda \ left (f \ left (x_1 \ right) -f \ left (x_3 \ right) \ right) + \ left (1- \ lambda \ right) \ left (f \ left (x_2 \ right) -f \ left (x_3 \ right) \ right) \ geq 0$

$\ Rightarrow f \ left (x_3 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right)$

теорема

пусть S — непустое открытое выпуклое множество в $\ mathbb {R} ^ n$, и пусть $f: S \ rightarrow \ mathbb {R}$ дифференцируемо на S, тогда f выпукло на S тогда и только тогда, когда для любой $x_1, x_2 \ in S, \ left (\ bigtriangledown f \ left (x_2 \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (x_2-x_1 \ right) \ geq 0$

доказательство

пусть f — выпуклая функция, тогда используя предыдущую теорему —

$\ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) \ leq f \ left (x_1 \ right) -f \ left (x_2 \ right)$ и

$\ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) \ leq f \ left (x_2 \ right) -f \ left (x_1 \ right)$

Сложив два приведенных выше уравнения, получим —

$\ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) + \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) \ leq 0$

$\ Rightarrow \ left (\ bigtriangledown f \ left (x_2 \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (x_1-x_2 \ right) \ leq 0$

$\ Rightarrow \ left (\ bigtriangledown f \ left (x_2 \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (x_2-x_1 \ right) \ geq 0$

обратный

Пусть для любого $x_1, x_2 \ in S, \ left (\ bigtriangledown f \ left (x_2 \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (x_2-x_1 \ right) \ geq 0$

Чтобы показать, что f выпуклая.

Пусть $x_1, x_2 \ in S$, то есть по теореме о среднем значении $\ frac {f \ left (x_1 \ right) -f \ left (x_2 \ right)} {x_1-x_2} = \ bigtriangledown f \ left ( x \ right), x \ in \ left (x_1-x_2 \ right) \ Rightarrow x = \ lambda x_1 + \ left (1- \ lambda \ right) x_2$, поскольку S — выпуклое множество.

$\ Rightarrow f \ left (x_1 \ right) - f \ left (x_2 \ right) = \ left (\ bigtriangledown f \ left (x \ right) ^ T \ right) \ left (x_1-x_2 \ right)$

за $x, x_1$ мы знаем —

$\ left (\ bigtriangledown f \ left (x \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (x-x_1 \ right) \ geq 0$

$\ Rightarrow \ left (\ bigtriangledown f \ left (x \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2- x_1 \ right) \ geq 0$

$\ Rightarrow \ left (\ bigtriangledown f \ left (x \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (1- \ lambda \ right) \ left (x_2-x_1 \ right) ) \ geq 0$

$\ Rightarrow \ bigtriangledown f \ left (x \ right) ^ T \ left (x_2-x_1 \ right) \ geq \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right)$

Комбинируя вышеприведенные уравнения, получим —

$\ Rightarrow \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) \ leq f \ left (x_2 \ right) -f \ left (x_1 \ right)$

Следовательно, используя последнюю теорему, f является выпуклой функцией.

Дважды дифференцируемая функция

Пусть S — непустое подмножество в $\ mathbb {R} ^ n$, и пусть $f: S \ rightarrow \ mathbb {R}$, тогда f называется дважды дифференцируемым в $\ bar {x} \ in S$, если существует вектор $\ bigtriangledown f \ left (\ bar {x} \ right), матрица \: nXn$ $H \ left (x \ right)$ (называемая гессианской матрицей) и функция $\ alpha: \ mathbb {R} ^ n \ rightarrow \ mathbb {R}$ такой, что $f \ left (x \ right) = f \ left (\ bar {x} + x- \ bar {x} \ right) = f \ left (\ bar {x} \ right) + \ bigtriangledown f \ left (\ bar {x} \ right) ^ T \ left (x- \ bar {x} \ right) + \ frac {1} {2} \ left (x- \ bar {x} \ right) H \ left (\ bar {x} \ right) \ left (x- \ bar {x} \ right)$

где $\ alpha \ left (\ bar {x}, x- \ bar {x} \ right) \ rightarrow Oasx \ rightarrow \ bar {x}$

Достаточные и необходимые условия для Global Optima

теорема

Пусть f — дважды дифференцируемая функция. Если $\ bar {x}$ является локальным минимумом, то $\ bigtriangledown f \ left (\ bar {x} \ right) = 0$ и гессенская матрица $H \ left (\ bar {x} \ right)$ является положительным полуопределенным.

доказательство

Пусть $d \ in \ mathbb {R} ^ n$. Поскольку f дважды дифференцируема в $\ bar {x}$.

Следовательно,

$f \ left (\ bar {x} + \ lambda d \ right) = f \ left (\ bar {x} \ right) + \ lambda \ bigtriangledown f \ left (\ bar {x} \ right) ^ T d + \ lambda ^ 2d ^ TH \ left (\ bar {x} \ right) d + \ lambda ^ 2d ^ TH \ left (\ bar {x} \ right) d +$

$ \ lambda ^ 2 \ left \ | d \ right \ | ^ 2 \ beta \ left (\ bar {x}, \ lambda d \ right) $

Но $\ bigtriangledown f \ left (\ bar {x} \ right) = 0$ и $\ beta \ left (\ bar {x}, \ lambda d \ right) \ rightarrow 0$ как $\ lambda \ rightarrow 0$

$\ Rightarrow f \ left (\ bar {x} + \ lambda d \ right) -f \ left (\ bar {x} \ right) = \ lambda ^ 2d ^ TH \ left (\ bar {x} \ right) d$

Поскольку $\ bar {x}$ является локальным минимумом, существует такое $\ delta&amp;gt; 0$, что $f \ left (x \ right) \ leq f \ left (\ bar {x} + \ lambda d \ right) ), \ forall \ lambda \ in \ left (0, \ delta \ right)$

теорема

Пусть $f: S \ rightarrow \ mathbb {R} ^ n$, где $S \ subset \ mathbb {R} ^ n$, можно дважды дифференцировать по S. Если $\ bigtriangledown f \ left (x \ right) = 0$ и $H \ left (\ bar {x} \ right)$ положительно полуопределен, для всех $x \ in S$ тогда $\ bar {x}$ является глобальным оптимальным решением.

доказательство

Поскольку $H \ left (\ bar {x} \ right)$ является положительно-полуопределенным, f является выпуклой функцией над S. Поскольку f дифференцируема и выпукла в $\ bar {x}$

$\ bigtriangledown f \ left (\ bar {x} \ right) ^ T \ left (x- \ bar {x} \ right) \ leq f \ left (x \ right) -f \ left (\ bar {x} \ right), \ forall x \ in S$

Так как $\ bigtriangledown f \ left (\ bar {x} \ right) = 0, f \ left (x \ right) \ geq f \ left (\ bar {x} \ right)$

Следовательно, $\ bar {x}$ является глобальной оптимой.

теорема

Предположим, что $\ bar {x} \ in S$ является локальным оптимальным решением задачи $f: S \ rightarrow \ mathbb {R}$, где S — непустое подмножество в $\ mathbb {R} ^ n$ и S выпуклый. $min \: f \ left (x \ right)$, где $x \ in S$.

Затем:

• $\ bar {x}$ — глобальное оптимальное решение.

• Если либо $\ bar {x}$ — строго локальные минимумы, либо f — строго выпуклая функция, то $\ bar {x}$ — единственное глобальное оптимальное решение, а также сильные локальные минимумы.

$\ bar {x}$ — глобальное оптимальное решение.

Если либо $\ bar {x}$ — строго локальные минимумы, либо f — строго выпуклая функция, то $\ bar {x}$ — единственное глобальное оптимальное решение, а также сильные локальные минимумы.

доказательство

Пусть $\ bar {x}$ — другое глобальное оптимальное решение задачи, такое что $x \ neq \ bar {x}$ и $f \ left (\ bar {x} \ right) = f \ left (\ hat { x} \ right)$

Поскольку $\ hat {x}, \ bar {x} \ in S$ и S выпуклый, то $\ frac {\ hat {x} + \ bar {x}} {2} \ in S$ и f строго выпукло.

$\ Rightarrow f \ left (\ frac {\ hat {x} + \ bar {x}} {2} \ right) &amp;lt;\ frac {1} {2} f \ left (\ bar {x} \ right) + \ frac {1} {2} f \ left (\ hat {x} \ right) = f \ left (\ hat {x} \ right)$

Это противоречие.

Следовательно, $\ hat {x}$ — единственное глобальное оптимальное решение.

следствие

Пусть $f: S \ subset \ mathbb {R} ^ n \ rightarrow \ mathbb {R}$ — выпуклая дифференцируемая функция, где $\ phi \ neq S \ subset \ mathbb {R} ^ n$ — выпуклое множество. Рассмотрим задачу $min f \ left (x \ right), x \ in S$, тогда $\ bar {x}$ является оптимальным решением, если $\ bigtriangledown f \ left (\ bar {x} \ right) ^ T \ left (x- \ bar {x} \ right) \ geq 0, \ forall x \ in S.$

доказательство

Пусть $\ bar {x}$ является оптимальным решением, т. Е. $F \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ in S$

$\ Rightarrow f \ left (x \ right) = f \ left (\ bar {x} \ right) \ geq 0$

$ f \ left (x \ right) = f \ left (\ bar {x} \ right) + \ bigtriangledown f \ left (\ bar {x} \ right) ^ T \ left (x- \ bar {x} \ правый) + \ левый \ | x- \ bar {x} \ right \ | \ alpha \ left (\ bar {x}, x- \ bar {x} \ right) $

где $\ alpha \ left (\ bar {x}, x- \ bar {x} \ right) \ rightarrow 0$ как $x \ rightarrow \ bar {x}$

$\ Rightarrow f \ left (x \ right) -f \ left (\ bar {x} \ right) = \ bigtriangledown f \ left (\ bar {x} \ right) ^ T \ left (x- \ bar {x) } \ right) \ geq 0$

следствие

Пусть f — дифференцируемая выпуклая функция в $\ bar {x}$, тогда $\ bar {x}$ — глобальный минимум, если $\ bigtriangledown f \ left (\ bar {x} \ right) = 0$

Примеры

• $f \ left (x \ right) = \ left (x ^ 2-1 \ right) ^ {3}, x \ in \ mathbb {R}$.

  $\ bigtriangledown f \ left (x \ right) = 0 \ Rightarrow x = -1,0,1$.

  $\ bigtriangledown ^ 2f \ left (\ pm 1 \ right) = 0, \ bigtriangledown ^ 2 f \ left (0 \ right) = 6&amp;gt; 0$.

  $f \ left (\ pm 1 \ right) = 0, f \ left (0 \ right) = - 1$

  Следовательно, $f \ left (x \ right) \ geq -1 = f \ left (0 \ right) \ Rightarrow f \ left (0 \ right) \ leq f \ left (x \ right) \ forall x \ in \ mathbb {R}$

• $f \ left (x \ right) = x \ log x$, определенный в $S = \ left \ {x \ in \ mathbb {R}, x&amp;gt; 0 \ right \}$.

  ${f} 'x = 1 + \ log x$

  ${Е} '' х = \ гидроразрыва {1} {х}&amp;gt; 0$

  Таким образом, эта функция является строго выпуклой.

• $f \ left (x \ right) = e ^ {x}, x \ in \ mathbb {R}$ строго выпуклый.

$f \ left (x \ right) = \ left (x ^ 2-1 \ right) ^ {3}, x \ in \ mathbb {R}$.

$\ bigtriangledown f \ left (x \ right) = 0 \ Rightarrow x = -1,0,1$.

$\ bigtriangledown ^ 2f \ left (\ pm 1 \ right) = 0, \ bigtriangledown ^ 2 f \ left (0 \ right) = 6&amp;gt; 0$.

$f \ left (\ pm 1 \ right) = 0, f \ left (0 \ right) = - 1$

Следовательно, $f \ left (x \ right) \ geq -1 = f \ left (0 \ right) \ Rightarrow f \ left (0 \ right) \ leq f \ left (x \ right) \ forall x \ in \ mathbb {R}$

$f \ left (x \ right) = x \ log x$, определенный в $S = \ left \ {x \ in \ mathbb {R}, x&amp;gt; 0 \ right \}$.

${f} 'x = 1 + \ log x$

${Е} '' х = \ гидроразрыва {1} {х}&amp;gt; 0$

Таким образом, эта функция является строго выпуклой.

$f \ left (x \ right) = e ^ {x}, x \ in \ mathbb {R}$ строго выпуклый.

Квазивыпуклые и квазивогнутые функции

Пусть $f: S \ rightarrow \ mathbb {R}$, где $S \ subset \ mathbb {R} ^ n$ — непустое выпуклое множество. Функция f называется квазивыпуклой, если для каждого $x_1, x_2 \ in S$ мы имеем $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq max \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}, \ lambda \ in \ left (0, 1 \ right)$

Например, $f \ left (x \ right) = x ^ {3}$

Пусть $f: S \ rightarrow R$, где $S \ subset \ mathbb {R} ^ n$ — непустое выпуклое множество. Функция f называется квазивыпуклой, если для каждого $x_1, x_2 \ in S$ мы имеем $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ geq min \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}, \ lambda \ in \ left (0, 1 \ right)$

замечания

• Каждая выпуклая функция квазивыпуклая, но обратное неверно.
• Функция, которая является квазивыпуклой и квазивогнутой, называется квазимонотонной.

теорема

Пусть $f: S \ rightarrow \ mathbb {R}$ и S — непустое выпуклое множество в $\ mathbb {R} ^ n$. Функция f является квазивыпуклой тогда и только тогда, когда $S _ {\ alpha} = \ left (x \ in S: f \ left (x \ right) \ leq \ alpha \ right \}$ выпукло для каждого действительного числа \ alpha $

доказательство

Пусть f квазивыпуклая на S.

Пусть $x_1, x_2 \ in S _ {\ alpha}$, поэтому $x_1, x_2 \ in S$ и $max \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \} \ leq \ alpha$

Пусть $\ lambda \ in \ left (0, 1 \ right)$ и пусть $x = \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ leq max \ left \ {f \ left (x_1 \ right) , f \ left (x_2 \ right) \ right \} \ Rightarrow x \ in S$

Таким образом, $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq max \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \} \ leq \ alpha$

Следовательно, $S _ {\ alpha}$ выпукло.

обратный

Пусть $S _ {\ alpha}$ является выпуклым для каждого $\ alpha$

$x_1, x_2 \ in S, \ lambda \ in \ left (0,1 \ right)$

$x = \ lambda x_1 + \ left (1- \ lambda \ right) x_2$

Пусть $x = \ lambda x_1 + \ left (1- \ lambda \ right) x_2$

Для $x_1, x_2 \ in S _ {\ alpha}, \ alpha = max \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}$

$\ Rightarrow \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ in S _ {\ alpha}$

$\ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ alpha$

Отсюда доказано.

теорема

Пусть $f: S \ rightarrow \ mathbb {R}$ и S — непустое выпуклое множество в $\ mathbb {R} ^ n$. Функция f квазивогнута в том и только в том случае, если $S _ {\ alpha} = \ left \ {x \ in S: f \ left (x \ right) \ geq \ alpha \ right \}$ выпукло для каждого действительного числа $\ альфа$.

теорема

Пусть $f: S \ rightarrow \ mathbb {R}$ и S — непустое выпуклое множество в $\ mathbb {R} ^ n$. Функция f квазимонотонна тогда и только тогда, когда $S _ {\ alpha} = \ left \ {x \ in S: f \ left (x \ right) = \ alpha \ right \}$ выпукла для каждого действительного числа $\ alpha$.

Дифференцируемая квазивыпуклая функция

теорема

Пусть S — непустое выпуклое множество в $\ mathbb {R} ^ n$ и $f: S \ rightarrow \ mathbb {R}$ — дифференцируемо на S, тогда f квазивыпукло тогда и только тогда, когда для любого $x_1, x_2 \ in S$ и $f \ left (x_1 \ right) \ leq f \ left (x_2 \ right)$, у нас есть $\ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_2-x_1 \ right) \ leq 0$

доказательство

Пусть f — квазивыпуклая функция.

Пусть $x_1, x_2 \ in S$ такие, что $f \ left (x_1 \ right) \ leq f \ left (x_2 \ right)$

По дифференцируемости f в $x_2, \ lambda \ in \ left (0, 1 \ right)$

$f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) = f \ left (x_2 + \ lambda \ left (x_1-x_2 \ right) \ right) = f \ left (x_2 \ right) ) + \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right)$

$ + \ lambda \ left \ | x_1-x_2 \ right \ | \ alpha \ left (x_2, \ lambda \ left (x_1-x_2 \ right) \ right) $

$\ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) -f \ left (x_2 \ right) -f \ left (x_2 \ right) = \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right)$

$ + \ lambda \ left \ | x_1-x_2 \ right \ | \ alpha \ left (x2, \ lambda \ left (x_1-x_2 \ right) \ right) $

Но поскольку f квазивыпуклая, $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq f \ left (x_2 \ right)$

$ \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) + \ lambda \ left \ | x_1-x_2 \ right \ | \ alpha \ left (x_2, \ lambda \ left (x_1, x_2 \ right) \ right) \ leq 0 $

Но $\ alpha \ left (x_2, \ lambda \ left (x_1, x_2 \ right) \ right) \ rightarrow 0$ при $\ lambda \ rightarrow 0$

Следовательно, $\ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) \ leq 0$

обратный

пусть для $x_1, x_2 \ in S$ и $f \ left (x_1 \ right) \ leq f \ left (x_2 \ right)$, $\ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1, x_2 \ right) \ leq 0$

Чтобы показать, что f квазивыпуклый, т. Е. $F \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq f \ left (x_2 \ right)$

Доказательство от противного

Предположим, существует $x_3 = \ lambda x_1 + \ left (1- \ lambda \ right) x_2$, такой что $f \ left (x_2 \ right) &amp;lt;f \ left (x_3 \ right)$ для некоторого $\ lambda \ in \ left (0, 1 \ right)$

Для $x_2$ и $x_3: \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_2-x_3 \ right) \ leq 0$

$\ Rightarrow - \ lambda \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_2-x_3 \ right) \ leq 0$

$\ Rightarrow \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1-x_2 \ right) \ geq 0$

Для $x_1$ и $x_3: \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1-x_3 \ right) \ leq 0$

$\ Rightarrow \ left (1- \ lambda \ right) \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1-x_2 \ right) \ leq 0$

$\ Rightarrow \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1-x_2 \ right) \ leq 0$

таким образом, из приведенных выше уравнений $\ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1-x_2 \ right) = 0$

Определите $U = \ left \ {x: f \ left (x \ right) \ leq f \ left (x_2 \ right), x = \ mu x_2 + \ left (1- \ mu \ right) x_3, \ mu \ in \ left (0,1 \ right) \ right \}$

Таким образом, мы можем найти $x_0 \ in U$ такой, что $x_0 = \ mu_0 x_2 = \ mu x_2 + \ left (1- \ mu \ right) x_3$ для некоторого $\ mu _0 \ in \ left (0,1 \ right) )$, ближайший к $x_3$ и $\ hat {x} \ in \ left (x_0, x_1 \ right)$, так что по теореме о среднем значении

$$\ frac {f \ left (x_3 \ right) -f \ left (x_0 \ right)} {x_3-x_0} = \ bigtriangledown f \ left (\ hat {x} \ right)$$

$$\ Rightarrow f \ left (x_3 \ right) = f \ left (x_0 \ right) + \ bigtriangledown f \ left (\ hat {x} \ right) ^ T \ left (x_3-x_0 \ right)$$

$$ \ Rightarrow f \ left (x_3 \ right) = f \ left (x_0 \ right) + \ mu_0 \ lambda f \ left (\ hat {x} \ right) ^ T \ left (x_1-x_2 \ right) $ $

Поскольку $x_0$ представляет собой комбинацию $x_1$ и $x_2$ и $f \ left (x_2 \ right) &amp;lt;f \ left (\ hat {x} \ right)$

Повторяя процедуру запуска, $\ bigtriangledown f \ left (\ hat {x} \ right) ^ T \ left (x_1-x_2 \ right) = 0$

Таким образом, объединяя приведенные выше уравнения, получаем:

$$f \ left (x_3 \ right) = f \ left (x_0 \ right) \ leq f \ left (x_2 \ right)$$

$$\ Rightarrow f \ left (x_3 \ right) \ leq f \ left (x_2 \ right)$$

Следовательно, это противоречие.

Примеры

Шаг 1 — $f \ left (x \ right) = X ^ 3$

$Пусть f \ left (x_1 \ right) \ leq f \ left (x_2 \ right)$

$\ Rightarrow x_ {1} ^ {3} \ leq x_ {2} ^ {3} \ Rightarrow x_1 \ leq x_2$

$\ bigtriangledown f \ left (x_2 \ right) \ left (x_1-x_2 \ right) = 3x_ {2} ^ {2} \ left (x_1-x_2 \ right) \ leq 0$

Таким образом, $f \ left (x \ right)$ является квазивыпуклым.

Шаг 2 — $f \ left (x \ right) = x_ {1} ^ {3} + x_ {2} ^ {3}$

Пусть $\ hat {x_1} = \ left (2, -2 \ right)$ и $\ hat {x_2} = \ left (1, 0 \ right)$

таким образом, $f \ left (\ hat {x_1} \ right) = 0, f \ left (\ hat {x_2} \ right) = 1 \ Rightarrow f \ left (\ hat {x_1} \ right) \ setminus &amp;lt;f \ left (\ hat {x_2} \ right)$

Таким образом, $\ bigtriangledown f \ left (\ hat {x_2} \ right) ^ T \ left (\ hat {x_1} - \ hat {x_2} \ right) = \ left (3, 0 \ right) ^ T \ left (1, -2 \ справа) = 3&amp;gt; 0$

Следовательно, $f \ left (x \ right)$ не является квазивыпуклым.

Строго квазивыпуклая функция

Пусть $f: S \ rightarrow \ mathbb {R} ^ n$ и S — непустое выпуклое множество в $\ mathbb {R} ^ n$, тогда f называется строго квазиковексной функцией, если для каждого $x_1, x_2 \ in S$ с $f \ left (x_1 \ right) \ neq f \ left (x_2 \ right)$, у нас есть $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) &amp;lt;max \: \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}$

замечания

• Каждая строго квазивыпуклая функция является строго выпуклой.
• Строго квазивыпуклая функция не подразумевает квазивыпуклости.
• Строго квазивыпуклая функция не может быть сильно квазивыпуклой.
• Псевдовыпуклая функция является строго квазивыпуклой функцией.

теорема

Пусть $f: S \ rightarrow \ mathbb {R} ^ n$ — строго квазивыпуклая функция, а S — непустое выпуклое множество в $\ mathbb {R} ^ n$. Рассмотрим проблему: $min \: f \ left (x \ right), x \ in S$. Если $\ hat {x}$ является локальным оптимальным решением, то $\ bar {x}$ является глобальным оптимальным решением.

доказательство

Пусть существует $\ bar {x} \ in S$ такой, что $f \ left (\ bar {x} \ right) \ leq f \ left (\ hat {x} \ right)$

Поскольку $\ bar {x}, \ hat {x} \ in S$ и S выпуклое множество, следовательно,

$$\ lambda \ bar {x} + \ left (1- \ lambda \ right) \ hat {x} \ in S, \ forall \ lambda \ in \ left (0,1 \ right)$$

Поскольку $\ hat {x}$ — локальные минимумы, $f \ left (\ hat {x} \ right) \ leq f \ left (\ lambda \ bar {x} + \ left (1- \ lambda \ right) \ hat {x} \ right), \ forall \ lambda \ in \ left (0, \ delta \ right)$

Поскольку f строго квазивыпуклый.

$$f \ left (\ lambda \ bar {x} + \ left (1- \ lambda \ right) \ hat {x} \ right) &amp;lt;max \ left \ {f \ left (\ hat {x} \ right) , f \ left (\ bar {x} \ right) \ right \} = f \ left (\ hat {x} \ right)$$

Следовательно, это противоречие.

Строго квазивогнутая функция

Пусть $f: S \ rightarrow \ mathbb {R} ^ n$ и S — непустое выпуклое множество в $\ mathbb {R} ^ n$, тогда f считается строго квазиковексной функцией, если для каждого $x_1, x_2 \ in S$ с $f \ left (x_1 \ right) \ neq f \ left (x_2 \ right)$, имеем

$$f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right)&amp;gt; min \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}$$ .

Примеры

• $f \ left (x \ right) = x ^ 2-2$

  Это строго квазивыпуклая функция, потому что если мы возьмем любые две точки $x_1, x_2$ в области, которые удовлетворяют ограничениям в определении $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) &amp;lt;max \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}$ Поскольку функция уменьшается по отрицательной оси x и увеличивается по положительной оси x ( так как это парабола).

• $f \ left (x \ right) = - x ^ 2$

  Это не строго квазивыпуклая функция, потому что если мы возьмем $x_1 = 1$ и $x_2 = -1$ и $\ lambda = 0.5$, то $f \ left (x_1 \ right) = - 1 = f \ left ( x_2 \ right)$ but $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) = 0$ Поэтому оно не удовлетворяет условиям, изложенным в определении. Но это квазивогнутая функция, потому что если мы возьмем любые две точки в области, которые удовлетворяют ограничениям в определении $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right)&amp;gt; min \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}$. Поскольку функция увеличивается в отрицательной оси X и уменьшается в положительной оси X.

$f \ left (x \ right) = x ^ 2-2$

Это строго квазивыпуклая функция, потому что если мы возьмем любые две точки $x_1, x_2$ в области, которые удовлетворяют ограничениям в определении $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) &amp;lt;max \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}$ Поскольку функция уменьшается по отрицательной оси x и увеличивается по положительной оси x ( так как это парабола).

$f \ left (x \ right) = - x ^ 2$

Это не строго квазивыпуклая функция, потому что если мы возьмем $x_1 = 1$ и $x_2 = -1$ и $\ lambda = 0.5$, то $f \ left (x_1 \ right) = - 1 = f \ left ( x_2 \ right)$ but $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) = 0$ Поэтому оно не удовлетворяет условиям, изложенным в определении. Но это квазивогнутая функция, потому что если мы возьмем любые две точки в области, которые удовлетворяют ограничениям в определении $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right)&amp;gt; min \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}$. Поскольку функция увеличивается в отрицательной оси X и уменьшается в положительной оси X.

Сильно квазивыпуклая функция

Пусть $f: S \ rightarrow \ mathbb {R} ^ n$ и S — непустое выпуклое множество в $\ mathbb {R} ^ n$, тогда f сильно квазивыпуклая функция, если для любого $x_1, x_2 \ in S$ с $\ left (x_1 \ right) \ neq \ left (x_2 \ right)$, у нас есть $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) &amp;lt;max \: \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}, \ forall \ lambda \ in \ left (0,1 \ right)$

теорема

Квазивыпуклая функция $f: S \ rightarrow \ mathbb {R} ^ n$ на непустом выпуклом множестве S в $\ mathbb {R} ^ n$ является сильно квазивыпуклой функцией, если она не постоянна на отрезке, соединяющем любую очки С.

доказательство

Пусть f — квазивыпуклая функция, и она не постоянна на отрезке, соединяющем любые точки S.

Предположим, что f не сильно квазивыпуклая функция.

Существуют $x_1, x_2 \ in S$ с $x_1 \ neq x_2$, такие что

$$f \ left (z \ right) \ geq max \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}, \ forall z = \ lambda x_1 + \ left (1 - \ lambda \ right) x_2, \ lambda \ in \ left (0,1 \ right)$$

$\ Rightarrow f \ left (x_1 \ right) \ leq f \ left (z \ right)$ и $f \ left (x_2 \ right) \ leq f \ left (z \ right)$

Поскольку f не является постоянной величиной в $\ left [x_1, z \ right]$ и $\ left [z, x_2 \ right]$

Таким образом, существует $u \ in \ left [x_1, z \ right]$ и $v = \ left [z, x_2 \ right]$

$$\ Rightarrow u = \ mu_1x_1 + \ left (1- \ mu_1 \ right) z, v = \ mu_2z + \ left (1- \ mu_2 \ right) x_2$$

Поскольку f квазивыпуклый,

$$\ Rightarrow f \ left (u \ right) \ leq max \ left \ {f \ left (x_1 \ right), f \ left (z \ right) \ right \} = f \ left (z \ right) \ : \: и \: \: f \ left (v \ right) \ leq max \ left \ {f \ left (z \ right), f \ left (x_2 \ right) \ right \}$$

$$ \ Rightarrow f \ left (u \ right) \ leq f \ left (z \ right) \: \: и \: \: f \ left (v \ right) \ leq f \ left (z \ right) $ $

$$\ Rightarrow max \ left \ {f \ left (u \ right), f \ left (v \ right) \ right \} \ leq f \ left (z \ right)$$

Но z — это любая точка между u и v, если любое из них равно, то f постоянно.

Следовательно, $max \ left \ {f \ left (u \ right), f \ left (v \ right) \ right \} \ leq f \ left (z \ right)$

что противоречит квазивыпуклости f как $z \ in \ left [u, v \ right]$.

Следовательно, f сильно квазивыпуклая функция.

теорема

Пусть $f: S \ rightarrow \ mathbb {R} ^ n$ и S — непустое выпуклое множество в $\ mathbb {R} ^ n$. Если $\ hat {x}$ — локальное оптимальное решение, то $\ hat {x}$ — единственное глобальное оптимальное решение.

доказательство

Поскольку сильная квазивыпуклая функция также является строго квазивыпуклой функцией, локальное оптимальное решение является глобальным оптимальным решением.

Единственность — Пусть f достигает глобального оптимального решения в двух точках $u, v \ in S$

$$\ Rightarrow f \ left (u \ right) \ leq f \ left (x \ right). \ Forall x \ in S \: \: и \: \: f \ left (v \ right) \ leq f \ влево (x \ right). \ forall x \ in S$$

Если u — глобальное оптимальное решение, $f \ left (u \ right) \ leq f \ left (v \ right)$ и $f \ left (v \ right) \ leq f \ left (u \ right) \ Rightarrow f \ left (u \ right) = f \ left (v \ right)$

$$f \ left (\ lambda u + \ left (1- \ lambda \ right) v \ right) &amp;lt;max \ left \ {f \ left (u \ right), f \ left (v \ right) \ right \} = f \ left (u \ right)$$

что противоречие.

Следовательно, существует только одно глобальное оптимальное решение.

замечания

• Сильно квазивыпуклая функция также является строго квазивыпуклой функцией.
• Строго выпуклая функция может быть или не быть сильно квазивыпуклой.
• Дифференцируемый строго выпуклый сильно квазивыпуклый.

Псевдовыпуклая функция

Пусть $f: S \ rightarrow \ mathbb {R}$ — дифференцируемая функция, а S — непустое выпуклое множество в $\ mathbb {R} ^ n$, тогда f называется псевдовыпуклым, если для каждого $x_1, x_2 \ in S$ с $\ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) \ geq 0$, у нас есть $f \ left (x_2 \ right) \ geq f \ left ( x_1 \ right)$, или эквивалентно, если $f \ left (x_1 \ right)&amp;gt; f \ left (x_2 \ right)$, то $\ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) ) &amp;lt;0$

Псевдо-вогнутая функция

Пусть $f: S \ rightarrow \ mathbb {R}$ — дифференцируемая функция, а S — непустое выпуклое множество в $\ mathbb {R} ^ n$, тогда f называется псевдовыпуклым, если для каждого $x_1, x_2 \ in S$ с $\ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) \ geq 0$, у нас есть $f \ left (x_2 \ right) \ leq f \ left ( x_1 \ right)$, или эквивалентно, если $f \ left (x_1 \ right)&amp;gt; f \ left (x_2 \ right)$, то $\ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) )&amp;gt; 0$

замечания

• Если функция является и псевдовыпуклой, и псевдовогнутой, то она называется псевдолинейной.

• Дифференцируемая выпуклая функция также является псевдовыпуклой.

• Псевдовыпуклая функция не может быть выпуклой. Например,

  $f \ left (x \ right) = x + x ^ 3$ не является выпуклым. Если $x_1 \ leq x_2, x_ {1} ^ {3} \ leq x_ {2} ^ {3}$

  Таким образом, $\ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) = \ left (1 + 3x_ {1} ^ {2} \ right) \ left (x_2-x_1 \ right) \ geq 0$

  И, $f \ left (x_2 \ right) -f \ left (x_1 \ right) = \ left (x_2-x_1 \ right) + \ left (x_ {2} ^ {3} -x_ {1} ^ {3 } \ right) \ geq 0$

  $\ Rightarrow f \ left (x_2 \ right) \ geq f \ left (x_1 \ right)$

  Таким образом, это псевдовыпуклый.

  Псевдовыпуклая функция строго квазивыпуклая. Таким образом, каждый локальный минимум псевдовыпуклости также является глобальным минимумом.

Если функция является и псевдовыпуклой, и псевдовогнутой, то она называется псевдолинейной.

Дифференцируемая выпуклая функция также является псевдовыпуклой.

Псевдовыпуклая функция не может быть выпуклой. Например,

$f \ left (x \ right) = x + x ^ 3$ не является выпуклым. Если $x_1 \ leq x_2, x_ {1} ^ {3} \ leq x_ {2} ^ {3}$

Таким образом, $\ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) = \ left (1 + 3x_ {1} ^ {2} \ right) \ left (x_2-x_1 \ right) \ geq 0$

И, $f \ left (x_2 \ right) -f \ left (x_1 \ right) = \ left (x_2-x_1 \ right) + \ left (x_ {2} ^ {3} -x_ {1} ^ {3 } \ right) \ geq 0$

$\ Rightarrow f \ left (x_2 \ right) \ geq f \ left (x_1 \ right)$

Таким образом, это псевдовыпуклый.

Псевдовыпуклая функция строго квазивыпуклая. Таким образом, каждый локальный минимум псевдовыпуклости также является глобальным минимумом.

Строго псевдовыпуклая функция

Пусть $f: S \ rightarrow \ mathbb {R}$ — дифференцируемая функция, а S — непустое выпуклое множество в $\ mathbb {R} ^ n$, тогда f называется псевдовыпуклым, если для каждого $x_1, x_2 \ in S$ с $\ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) \ geq 0$, у нас есть $f \ left (x_2 \ right)&amp;gt; f \ left (x_1 \ right)$ или, что эквивалентно, если $f \ left (x_1 \ right) \ geq f \ left (x_2 \ right)$ then $\ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) ) &amp;lt;0$

теорема

Пусть f — псевдовыпуклая функция, и пусть $\ bigtriangledown f \ left (\ hat {x} \ right) = 0$ для некоторого $\ hat {x} \ in S$, тогда $\ hat {x}$ является глобально оптимальным решение е над S.

доказательство

Пусть $\ hat {x}$ — критическая точка f, т. Е. $\ Bigtriangledown f \ left (\ hat {x} \ right) = 0$

Поскольку f — псевдовыпуклая функция, для $x \ in S,$ имеем

$$\ bigtriangledown f \ left (\ hat {x} \ right) \ left (x- \ hat {x} \ right) = 0 \ Rightarrow f \ left (\ hat {x} \ right) \ leq f \ left (x \ right), \ forall x \ in S$$

Следовательно, $\ hat {x}$ является глобальным оптимальным решением.

замечание

Если f — строго псевдовыпуклая функция, $\ hat {x}$ — единственное глобальное оптимальное решение.

теорема

Если f — дифференцируемая псевдовыпуклая функция над S, то f является как строго квазивыпуклой, так и квазивыпуклой функцией.

замечания

• Сумма двух псевдовыпуклых функций, определенных на открытом множестве S из $\ mathbb {R} ^ n$, не может быть псевдовыпуклой.

• Пусть $f: S \ rightarrow \ mathbb {R}$ — квазивыпуклая функция, а S — непустое выпуклое подмножество в $\ mathbb {R} ^ n$, тогда f является псевдовыпуклым тогда и только тогда, когда каждая критическая точка является глобальной минимумы f над S.

• Пусть S — непустое выпуклое подмножество в $\ mathbb {R} ^ n$, а $f: S \ rightarrow \ mathbb {R}$ — такая функция, что $\ bigtriangledown f \ left (x \ right) \ neq 0$ для каждого $x \ in S$, то f является псевдовыпуклой тогда и только тогда, когда она является квазивыпуклой функцией.

Сумма двух псевдовыпуклых функций, определенных на открытом множестве S из $\ mathbb {R} ^ n$, не может быть псевдовыпуклой.

Пусть $f: S \ rightarrow \ mathbb {R}$ — квазивыпуклая функция, а S — непустое выпуклое подмножество в $\ mathbb {R} ^ n$, тогда f является псевдовыпуклым тогда и только тогда, когда каждая критическая точка является глобальной минимумы f над S.

Пусть S — непустое выпуклое подмножество в $\ mathbb {R} ^ n$, а $f: S \ rightarrow \ mathbb {R}$ — такая функция, что $\ bigtriangledown f \ left (x \ right) \ neq 0$ для каждого $x \ in S$, то f является псевдовыпуклой тогда и только тогда, когда она является квазивыпуклой функцией.

Выпуклая оптимизация — проблема программирования

Существует четыре типа задач выпуклого программирования:

Шаг 1 — $min \: f \ left (x \ right)$, где $x \ in S$ и S — непустое выпуклое множество в $\ mathbb {R} ^ n$ и $f \ left (x \ right)$ — выпуклая функция.

Шаг 2 — $min \: f \ left (x \ right), x \ in \ mathbb {R} ^ n$ при условии

$g_i \ left (x \ right) \ geq 0, 1 \ leq m_1$ и $g_i \ left (x \ right)$ — выпуклая функция.

$g_i \ left (x \ right) \ leq 0, m_1 + 1 \ leq m_2$ и $g_i \ left (x \ right)$ — вогнутая функция.

$g_i \ left (x \ right) = 0, m_2 + 1 \ leq m$ и $g_i \ left (x \ right)$ — линейная функция.

где $f \ left (x \ right)$ — выпуклая функция.

Шаг 3 — $max \: f \ left (x \ right)$, где $x \ in S$ и S — непустое выпуклое множество в $\ mathbb {R} ^ n$ и $f \ left (x \) справа)$ — вогнутая функция.

Шаг 4 — $min \: f \ left (x \ right)$, где $x \ in \ mathbb {R} ^ n$ подчиняется

$g_i \ left (x \ right) \ geq 0, 1 \ leq m_1$ и $g_i \ left (x \ right)$ — выпуклая функция.

$g_i \ left (x \ right) \ leq 0, m_1 + 1 \ leq m_2$ и $g_i \ left (x \ right)$ — вогнутая функция.

$g_i \ left (x \ right) = 0, m_2 + 1 \ leq m$ и $g_i \ left (x \ right)$ — линейная функция.

где $f \ left (x \ right)$ — вогнутая функция.

Конус возможного направления

Пусть S — непустое множество в $\ mathbb {R} ^ n$, и пусть $\ hat {x} \ in \: Closure \ left (S \ right)$, тогда конус допустимого направления S в $\ hat {x}$, обозначаемый D, определяется как $D = \ left \ {d: d \ neq 0, \ hat {x} + \ lambda d \ in S, \ lambda \ in \ left (0, \ delta \ right), \ delta&amp;gt; 0 \ right \}$

Каждый ненулевой вектор $d \ in D$ называется допустимым направлением.

Для данной функции $f: \ mathbb {R} ^ n \ Rightarrow \ mathbb {R}$ конус улучшения направления в $\ hat {x}$ обозначается через F и определяется как

$$F = \ left \ {d: f \ left (\ hat {x} + \ lambda d \ right) \ leq f \ left (\ hat {x} \ right), \ forall \ lambda \ in \ left ( 0, \ delta \ right), \ delta&amp;gt; 0 \ right \}$$

Каждое направление $d \ in F$ называется улучшающим направлением или направлением спуска f в $\ hat {x}$

теорема

Необходимое условие

Рассмотрим задачу $min f \ left (x \ right)$, в которой $x \ in S$, где S — непустое множество в $\ mathbb {R} ^ n$. Предположим, что f дифференцируема в точке $\ hat {x} \ in S$. Если $\ hat {x}$ является локальным оптимальным решением, то $F_0 \ cap D = \ phi$, где $F_0 = \ left \ {d: \ bigtriangledown f \ left (\ hat {x} \ right) ^ T d &amp;lt;0 \ right \}$, а D — конус возможного направления.

Достаточное условие

Если $F_0 \ cap D = \ phi$ f является псевдовыпуклой функцией в $\ hat {x}$ и существует окрестность $\ hat {x}, N_ \ varepsilon \ left (\ hat {x} \ right) , \ varepsilon&amp;gt; 0$ такое, что $d = x- \ hat {x} \ in D$ для любого $x \ in S \ cap N_ \ varepsilon \ left (\ hat {x} \ right)$, затем $\ hat {x}$ — локально оптимальное решение.

доказательство

Необходимое условие

Пусть $F_0 \ cap D \ neq \ phi$, т. Е. Существует такое $d \ in F_0 \ cap D$, что $d \ in F_0$ и $d \ in D$

Поскольку $d \ in D$, существует $\ delta_1&amp;gt; 0$, для которого $\ hat {x} + \ lambda d \ in S, \ lambda \ in \ left (0, \ delta_1 \ right).$

Так как $d \ in F_0$, поэтому $\ bigtriangledown f \ left (\ hat {x} \ right) ^ T d &amp;lt;0$

Таким образом, существует $\ delta_2&amp;gt; 0$ такое, что $f \ left (\ hat {x} + \ lambda d \ right) &amp;lt;f \ left (\ hat {x} \ right), \ forall \ lambda \ in f \ left (0, \ delta_2 \ right)$

Пусть $\ delta = min \ left \ {\ delta_1, \ delta_2 \ right \}$

Тогда $\ hat {x} + \ lambda d \ in S, f \ left (\ hat {x} + \ lambda d \ right) &amp;lt;f \ left (\ hat {x} \ right), \ forall \ lambda \ в f \ left (0, \ delta \ right)$

Но $\ hat {x}$ является локальным оптимальным решением.

Отсюда и противоречие.

Таким образом, $F_0 \ cap D = \ phi$

Достаточное условие

Пусть $F_0 \ cap D \ neq \ phi$ nd и f — псевдовыпуклая функция.

Пусть существует такая окрестность $\ hat {x}, N _ {\ varepsilon} \ left (\ hat {x} \ right)$, что $d = x- \ hat {x}, \ forall x \ in S \ колпачок N_ \ varepsilon \ left (\ hat {x} \ right)$

Пусть $\ hat {x}$ не является локальным оптимальным решением.

Таким образом, существует $\ bar {x} \ in S \ cap N_ \ varepsilon \ left (\ hat {x} \ right)$, такой что $f \ left (\ bar {x} \ right) &amp;lt;f \ left ( \ hat {x} \ right)$

По предположению $S \ cap N_ \ varepsilon \ left (\ hat {x} \ right), d = \ left (\ bar {x} - \ hat {x} \ right) \ in D$

По псевдовыпуклости f,

$$f \ left (\ hat {x} \ right)&amp;gt; f \ left (\ bar {x} \ right) \ Rightarrow \ bigtriangledown f \ left (\ hat {x} \ right) ^ T \ left (\ bar {x} - \ hat {x} \ right) &amp;lt;0$$

$\ Rightarrow \ bigtriangledown f \ left (\ hat {x} \ right) ^ T d &amp;lt;0$

$\ Rightarrow d \ in F_0$

следовательно, $F_0 \ cap D \ neq \ phi$

что противоречие.

Следовательно, $\ hat {x}$ является локальным оптимальным решением.

Рассмотрим следующую задачу: $min \: f \ left (x \ right)$, где $x \ in X$ такое, что $g_x \ left (x \ right) \ leq 0, i = 1,2, ..., м$

$f: X \ rightarrow \ mathbb {R}, g_i: X \ rightarrow \ mathbb {R} ^ n$, а X — открытое множество в $\ mathbb {R} ^ n$

Пусть $S = \ left \ {x: g_i \ left (x \ right) \ leq 0, \ forall i \ right \}$

Пусть $\ hat {x} \ in X$, тогда $M = \ left \ {1,2, ..., m \ right \}$

Пусть $I = \ left \ {i: g_i \ left (\ hat {x} \ right) = 0, i \ in M ​​\ right \}$, где I называется набором индексов для всех активных ограничений в $\ hat {x }$

Пусть $J = \ left \ {i: g_i \ left (\ hat {x} \ right) &amp;lt;0, i \ in M ​​\ right \}$, где J называется набором индексов для всех активных ограничений в $\ hat {x }$.

Пусть $F_0 = \ left \ {d \ in \ mathbb {R} ^ m: \ bigtriangledown f \ left (\ hat {x} \ right) ^ T d &amp;lt;0 \ right \}$

Пусть $G_0 = \ left \ {d \ in \ mathbb {R} ^ m: \ bigtriangledown gI \ left (\ hat {x} \ right) ^ T d &amp;lt;0 \ right \}$

или $G_0 = \ left \ {d \ in \ mathbb {R} ^ m: \ bigtriangledown gi \ left (\ hat {x} \ right) ^ T d &amp;lt;0, \ forall i \ in I \ right \}$

лемма

Если $S = \ left \ {x \ in X: g_i \ left (x \ right) \ leq 0, \ forall i \ in I \ right \}$ и X — непустое открытое множество в $\ mathbb {R } ^ N$. Пусть $\ hat {x} \ in S$ и $g_i$ различны в $\ hat {x}, i \ in I$, и пусть $g_i$, где $i \ in J$ непрерывны в $\ hat {x }$, затем $G_0 \ subseteq D$.

доказательство

Пусть $d \ in G_0$

Поскольку $\ hat {x} \ in X$ и X — открытое множество, таким образом, существует $\ delta_1&amp;gt; 0$ такое, что $\ hat {x} + \ lambda d \ in X$ для $\ lambda \ in \ влево (0, \ delta_1 \ right)$

Также, так как $g_ \ hat {x} &amp;lt;0$ и $g_i$ непрерывны в $\ hat {x}, \ forall i \ in J$, существует $\ delta_2&amp;gt; 0$, $g_i \ left (\ hat {x} + \ lambda d \ right) &amp;lt;0, \ lambda \ in \ left (0, \ delta_2 \ right)$

Так как $d \ in G_0$, следовательно, $\ bigtriangledown g_i \ left (\ hat {x} \ right) ^ T d &amp;lt;0, \ forall i \ in I$, таким образом, существует $\ delta_3&amp;gt; 0, g_i \ left (\ hat {x} + \ lambda d \ right) &amp;lt;g_i \ left (\ hat {x} \ right) = 0$, для $\ lambda \ in \ left (0, \ delta_3 \ right) i \ in J$

Пусть $\ delta = min \ left \ {\ delta_1, \ delta_2, \ delta_3 \ right \}$

следовательно, $\ hat {x} + \ lambda d \ in X, g_i \ left (\ hat {x} + \ lambda d \ right) &amp;lt;0, i \ in M ​​$

$\ Rightarrow \ hat {x} + \ lambda d \ in S$

$\ Rightarrow d \ in D$

$\ Rightarrow G_0 \ subseteq D$

Отсюда доказано.

теорема

Необходимое условие

Пусть $f$ и $g_i, i \ in I$, различны в $\ hat {x} \ in S,$ и $g_j$ непрерывны в $\ hat {x} \ in S$. Если $\ hat {x}$ является локальным минимумом $S$, то $F_0 \ cap G_0 = \ phi$.

Достаточное условие

Если $F_0 \ cap G_0 = \ phi$ и f — псевдовыпуклая функция в $\ left (\ hat {x}, g_i 9x \ right), i \ in I$ — строго псевдовыпуклые функции над некоторой $\ varepsilon$ — окрестностью $\ hat {x}, \ hat {x}$ — локальное оптимальное решение.

замечания

• Пусть $\ hat {x}$ — допустимая точка, такая, что $\ bigtriangledown f \ left (\ hat {x} \ right) = 0$, тогда $F_0 = \ phi$. Таким образом, $F_0 \ cap G_0 = \ phi$, но $\ hat {x}$ не является оптимальным решением

• Но если $\ bigtriangledown g \ left (\ hat {x} \ right) = 0$, то $G_0 = \ phi$, то есть $F_0 \ cap G_0 = \ phi$

• Рассмотрим задачу: min $f \ left (x \ right)$ такое, что $g \ left (x \ right) = 0$.

  Так как $g \ left (x \ right) = 0$, то $g_1 \ left (x \ right) = g \ left (x \ right) &amp;lt;0$ и $g_2 \ left (x \ right) = - g \ left (x \ right) \ leq 0$.

  Пусть $\ hat {x} \ in S$, тогда $g_1 \ left (\ hat {x} \ right) = 0$ и $g_2 \ left (\ hat {x} \ right) = 0$.

  Но $\ bigtriangledown g_1 \ left (\ hat {x} \ right) = - \ bigtriangledown g_2 \ left (\ hat {x} \ right)$

  Таким образом, $G_0 = \ phi$ и $F_0 \ cap G_0 = \ phi$.

Пусть $\ hat {x}$ — допустимая точка, такая, что $\ bigtriangledown f \ left (\ hat {x} \ right) = 0$, тогда $F_0 = \ phi$. Таким образом, $F_0 \ cap G_0 = \ phi$, но $\ hat {x}$ не является оптимальным решением

Но если $\ bigtriangledown g \ left (\ hat {x} \ right) = 0$, то $G_0 = \ phi$, то есть $F_0 \ cap G_0 = \ phi$

Рассмотрим задачу: min $f \ left (x \ right)$ такое, что $g \ left (x \ right) = 0$.

Так как $g \ left (x \ right) = 0$, то $g_1 \ left (x \ right) = g \ left (x \ right) &amp;lt;0$ и $g_2 \ left (x \ right) = - g \ left (x \ right) \ leq 0$.

Пусть $\ hat {x} \ in S$, тогда $g_1 \ left (\ hat {x} \ right) = 0$ и $g_2 \ left (\ hat {x} \ right) = 0$.

Но $\ bigtriangledown g_1 \ left (\ hat {x} \ right) = - \ bigtriangledown g_2 \ left (\ hat {x} \ right)$

Таким образом, $G_0 = \ phi$ и $F_0 \ cap G_0 = \ phi$.

Выпуклая оптимизация — условия Фрица-Джона

Необходимые условия

теорема

Рассмотрим задачу — $min f \ left (x \ right)$, для которой $x \ in X$, где X — открытое множество в $\ mathbb {R} ^ n$, и пусть $g_i \ left (x \ right) \ leq 0, \ forall i = 1,2, .... m$.

Пусть $f: X \ rightarrow \ mathbb {R}$ и $g_i: X \ rightarrow \ mathbb {R}$

Пусть $\ hat {x}$ — допустимое решение, и пусть f и $g_i, i \ in I$ дифференцируемы в $\ hat {x}$, а $g_i, i \ in J$ непрерывны в $\ hat { х}$.

Если $\ hat {x}$ решает вышеуказанную проблему локально, то существует $u_0, u_i \ in \ mathbb {R}, i \ in I$, такой, что $u_0 \ bigtriangledown f \ left (\ hat {x} \ справа) + \ displaystyle \ sum \ limit_ {i \ in I} u_i \ bigtriangledown g_i \ left (\ hat {x} \ right)$ = 0

где $u_0, u_i \ geq 0, i \ in I$ и $\ left (u_0, u_I \ right) \ neq \ left (0,0 \ right)$

Кроме того, если $g_i, i \ in J$ также дифференцируемы в $\ hat {x}$, то вышеуказанные условия можно записать в виде —

$u_0 \ bigtriangledown f \ left (\ hat {x} \ right) + \ displaystyle \ sum \ limit_ {i = 1} ^ m u_i \ bigtriangledown g_i \ left (\ hat {x} \ right) = 0$

$u_ig_i \ left (\ hat {x} \ right)$ = 0

$u_0, u_i \ geq 0, \ forall i = 1,2, ...., m$

$\ left (u_0, u \ right) \ neq \ left (0,0 \ right), u = \ left (u_1, u_2, s, u_m \ right) \ in \ mathbb {R} ^ m$

замечания

• $u_i$ называются лагранжевыми множителями.

• Условие, что $\ hat {x}$ выполнимо для данной проблемы, называется первичным выполнимым условием.

• Требование $u_0 \ bigtriangledown f \ left (\ hat {x} \ right) + \ displaystyle \ sum \ limit_ {i = 1} ^ m ui \ bigtriangledown g_i \ left (x \ right) = 0$ называется двойной осуществимостью состояние.

• Условие $u_ig_i \ left (\ hat {x} \ right) = 0, i = 1, 2, ... m$ называется условием дополнительной слабости. Это условие требует $u_i = 0, i \ in J$

• Вместе первичное выполнимое условие, двойное условие выполнимости и комплиментарное расслабление называются условиями Фрица-Джона.

$u_i$ называются лагранжевыми множителями.

Условие, что $\ hat {x}$ выполнимо для данной проблемы, называется первичным выполнимым условием.

Требование $u_0 \ bigtriangledown f \ left (\ hat {x} \ right) + \ displaystyle \ sum \ limit_ {i = 1} ^ m ui \ bigtriangledown g_i \ left (x \ right) = 0$ называется двойной осуществимостью состояние.

Условие $u_ig_i \ left (\ hat {x} \ right) = 0, i = 1, 2, ... m$ называется условием дополнительной слабости. Это условие требует $u_i = 0, i \ in J$

Вместе первичное выполнимое условие, двойное условие выполнимости и комплиментарное расслабление называются условиями Фрица-Джона.

Достаточные условия

теорема

Если существует $\ varepsilon$ -соседство $\ hat {x} N_ \ varepsilon \ left (\ hat {x} \ right), \ varepsilon&amp;gt; 0$ такое, что f является псевдовыпуклым над $N_ \ varepsilon \ left ( \ hat {x} \ right) \ cap S$ и $g_i, i \ in I$ строго псевдовыпуклы над $N_ \ varepsilon \ left (\ hat {x} \ right) \ cap S$, затем $\ hat { x}$ — локальное оптимальное решение задачи, описанной выше. Если f является псевдовыпуклым в $\ hat {x}$ и если $g_i, i \ in I$ являются строго псевдовыпуклой и квазивыпуклой функцией в $\ hat {x}, \ hat {x}$ является глобальным оптимальным решением задачи описано выше.

пример

• $min \: f \ left (x_1, x_2 \ right) = \ left (x_1-3 \ right) ^ 2 + \ left (x_2-2 \ right) ^ 2$

  так что $x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 5, x_1 + 2x_2 \ leq 4, x_1, x_2 \ geq 0$ и $\ hat {x} = \ left (2 , 1 \ справа)$

  Пусть $g_1 \ left (x_1, x_2 \ right) = x_ {1} ^ {2} + x_ {2} ^ {2} -5,$

  $g_2 \ left (x_1, x_2 \ right) = x_1 + 2x_2-4,$

  $g_3 \ left (x_1, x_2 \ right) = - x_1$ и $g_4 \ left (x_1, x_2 \ right) = -x_2$.

  Таким образом, вышеуказанные ограничения могут быть записаны как —

  $g_1 \ left (x_1, x_2 \ right) \ leq 0,$

  $g_2 \ left (x_1, x_2 \ right) \ leq 0,$

  $g_3 \ left (x_1, x_2 \ right) \ leq 0$ и

  $g_4 \ left (x_1, x_2 \ right) \ leq 0$ Таким образом, $I = \ left \ {1,2 \ right \}$, следовательно, $u_3 = 0, u_4 = 0$

  $\ bigtriangledown f \ left (\ hat {x} \ right) = \ left (2, -2 \ right), \ bigtriangledown g_1 \ left (\ hat {x} \ right) = \ left (4,2 \ right) )$ и $\ bigtriangledown g_2 \ left (\ hat {x} \ right) = \ left (1,2 \ right)$

  Таким образом, помещая эти значения в первое условие условий Фрица-Джона, мы получаем —

  $u_0 = \ frac {3} {2} u_2, \: \: u_1 = \ frac {1} {2} u_2,$ и пусть $u_2 = 1$, поэтому $u_0 = \ frac {3} {2} , \: \: u_1 = \ frac {1} {2}$

  Таким образом, условия Фрица Джона удовлетворены.

• $min f \ left (x_1, x_2 \ right) = - x_1$.

  такой, что $x_2- \ left (1-x_1 \ right) ^ 3 \ leq 0$,

  $-x_2 \ leq 0$ и $\ hat {x} = \ left (1,0 \ right)$

  Пусть $g_1 \ left (x_1, x_2 \ right) = x_2- \ left (1-x_1 \ right) ^ 3$,

  $g_2 \ left (x_1, x_2 \ right) = - x_2$

  Таким образом, вышеуказанные ограничения можно записать как —

  $g_1 \ left (x_1, x_2 \ right) \ leq 0,$

  $g_2 \ left (x_1, x_2 \ right) \ leq 0,$

  Таким образом, $I = \ left \ {1,2 \ right \}$

  $\ bigtriangledown f \ left (\ hat {x} \ right) = \ left (-1,0 \ right)$

  $\ bigtriangledown g_1 \ left (\ hat {x} \ right) = \ left (0,1 \ right)$ и $g_2 \ left (\ hat {x} \ right) = \ left (0, -1 \ right) )$

  Таким образом, помещая эти значения в первое условие условий Фрица-Джона, мы получаем —

  $u_0 = 0, \: \: u_1 = u_2 = a&amp;gt; 0$

  Таким образом, условия Фрица Джона удовлетворены.

$min \: f \ left (x_1, x_2 \ right) = \ left (x_1-3 \ right) ^ 2 + \ left (x_2-2 \ right) ^ 2$

так что $x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 5, x_1 + 2x_2 \ leq 4, x_1, x_2 \ geq 0$ и $\ hat {x} = \ left (2 , 1 \ справа)$

Пусть $g_1 \ left (x_1, x_2 \ right) = x_ {1} ^ {2} + x_ {2} ^ {2} -5,$

$g_2 \ left (x_1, x_2 \ right) = x_1 + 2x_2-4,$

$g_3 \ left (x_1, x_2 \ right) = - x_1$ и $g_4 \ left (x_1, x_2 \ right) = -x_2$.

Таким образом, вышеуказанные ограничения могут быть записаны как —

$g_1 \ left (x_1, x_2 \ right) \ leq 0,$

$g_2 \ left (x_1, x_2 \ right) \ leq 0,$

$g_3 \ left (x_1, x_2 \ right) \ leq 0$ и

$g_4 \ left (x_1, x_2 \ right) \ leq 0$ Таким образом, $I = \ left \ {1,2 \ right \}$, следовательно, $u_3 = 0, u_4 = 0$

$\ bigtriangledown f \ left (\ hat {x} \ right) = \ left (2, -2 \ right), \ bigtriangledown g_1 \ left (\ hat {x} \ right) = \ left (4,2 \ right) )$ и $\ bigtriangledown g_2 \ left (\ hat {x} \ right) = \ left (1,2 \ right)$

Таким образом, помещая эти значения в первое условие условий Фрица-Джона, мы получаем —

$u_0 = \ frac {3} {2} u_2, \: \: u_1 = \ frac {1} {2} u_2,$ и пусть $u_2 = 1$, поэтому $u_0 = \ frac {3} {2} , \: \: u_1 = \ frac {1} {2}$

Таким образом, условия Фрица Джона удовлетворены.

$min f \ left (x_1, x_2 \ right) = - x_1$.

такой, что $x_2- \ left (1-x_1 \ right) ^ 3 \ leq 0$,

$-x_2 \ leq 0$ и $\ hat {x} = \ left (1,0 \ right)$

Пусть $g_1 \ left (x_1, x_2 \ right) = x_2- \ left (1-x_1 \ right) ^ 3$,

$g_2 \ left (x_1, x_2 \ right) = - x_2$

Таким образом, вышеуказанные ограничения можно записать как —

$g_1 \ left (x_1, x_2 \ right) \ leq 0,$

$g_2 \ left (x_1, x_2 \ right) \ leq 0,$

Таким образом, $I = \ left \ {1,2 \ right \}$

$\ bigtriangledown f \ left (\ hat {x} \ right) = \ left (-1,0 \ right)$

$\ bigtriangledown g_1 \ left (\ hat {x} \ right) = \ left (0,1 \ right)$ и $g_2 \ left (\ hat {x} \ right) = \ left (0, -1 \ right) )$

Таким образом, помещая эти значения в первое условие условий Фрица-Джона, мы получаем —

$u_0 = 0, \: \: u_1 = u_2 = a&amp;gt; 0$

Таким образом, условия Фрица Джона удовлетворены.

Каруш-Кун-Такер Оптимальность Необходимые условия

Рассмотрим проблему —

$min \: f \ left (x \ right)$ такое, что $x \ in X$, где X — открытое множество в $\ mathbb {R} ^ n$ и $g_i \ left (x \ right) \ leq 0, i = 1, 2, ..., m$

Пусть $S = \ left \ {x \ in X: g_i \ left (x \ right) \ leq 0, \ forall i \ right \}$

Пусть $\ hat {x} \ in S$ и $f$ и $g_i, i \ in I$ дифференцируемы в $\ hat {x}$, а $g_i, i \ in J$ непрерывны в $\ hat {х}$. Кроме того, $\ bigtriangledown g_i \ left (\ hat {x} \ right), i \ in I$ линейно независимы. Если $\ hat {x}$ решает вышеуказанную проблему локально, то существует $u_i, i \ in I$, такой что

$\ bigtriangledown f \ left (x \ right) + \ displaystyle \ sum \ limit_ {i \ in I} u_i \ bigtriangledown g_i \ left (\ hat {x} \ right) = 0$, $\: \: u_i \ geq 0, i \ in I$

Если $g_i, i \ in J$ также дифференцируемы в $\ hat {x}$. затем $\ hat {x}$, затем

$\ bigtriangledown f \ left (\ hat {x} \ right) + \ displaystyle \ sum \ limit_ {i = 1} ^ m u_i \ bigtriangledown g_i \ left (\ hat {x} \ right) = 0$

$u_ig_i \ left (\ hat {x} \ right) = 0, \ forall i = 1,2, ..., m$

$u_i \ geq 0 \ forall i = 1,2, ..., m$

пример

Рассмотрим следующую проблему —

$min \: f \ left (x_1, x_2 \ right) = \ left (x_1-3 \ right) ^ 2 + \ left (x_2-2 \ right) ^ 2$

такой, что $x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 5$,

$x_1,2x_2 \ geq 0$ и $\ hat {x} = \ left (2,1 \ right)$

Пусть $g_1 \ left (x_1, x_2 \ right) = x_ {1} ^ {2} + x_ {2} ^ {2} -5$,

$g_2 \ left (x_1, x_2 \ right) = x_ {1} + 2x_2-4$

$g_3 \ left (x_1, x_2 \ right) = - x_ {1}$ и $g_4 \ left (x_1, x_2 \ right) = - x_2$

Таким образом, вышеуказанные ограничения могут быть записаны как —

$g_1 \ left (x_1, x_2 \ right) \ leq 0, g_2 \ left (x_1, x_2 \ right) \ leq 0$

$g_3 \ left (x_1, x_2 \ right) \ leq 0,$ и $g_4 \ left (x_1, x_2 \ right) \ leq 0$ Таким образом, поэтому $I = \ left \ {1,2 \ right \}$ , $u_3 = 0, \: \: u_4 = 0$

$\ bigtriangledown f \ left (\ hat {x} \ right) = \ left (2, -2 \ right), \ bigtriangledown g_1 \ left (\ hat {x} \ right) = \ left (4,2 \ right) )$ и

$\ bigtriangledown g_2 \ left (\ hat {x} \ right) = \ left (1,2 \ right)$

Таким образом, помещая эти значения в первое условие условий Каруша-Куна-Такера, мы получаем —

$u_1 = \ frac {1} {3}$ и $u_2 = \ frac {2} {3}$

Таким образом, условия Каруша-Куна-Такера выполняются.

Алгоритмы для выпуклой задачи

Метод наискорейшего спуска

Этот метод также называется методом градиента или методом Коши. Этот метод включает в себя следующие термины —

$$X_ {к + 1} = x_k + \ alpha_kd_k$$

$d_k = - \ bigtriangledown f \ left (x_k \ right)$ или $ d_k = — \ frac {\ bigtriangledown f \ left (x_k \ right)} {\ left \ | \ bigtriangledown f \ left (x_k \ right) \ right \ |} $

Пусть $\ phi \ left (\ alpha \ right) = f \ left (x_k + \ alpha d_k \ right)$

Дифференцируя $\ phi$ и приравнивая его к нулю, мы можем получить $\ alpha$.

Таким образом, алгоритм выглядит следующим образом —

• Инициализируйте $x_0$, $\ varepsilon_1$, $\ varepsilon_2$ и установите $k = 0$.

• Установите $d_k = - \ bigtriangledown f \ left (x_k \ right)$ или $d_k = - \ frac {\ bigtriangledown f \ left (x_k \ right)} {\ left \ | \ bigtriangledown f \ left (x_k \ right) \ right \ |}$.

• найдите $\ alpha_k$ таким образом, чтобы минимизировать $\ phi \ left (\ alpha \ right) = f \ left (x_k + \ alpha d_k \ right)$.

• Установите $x_ {k + 1} = x_k + \ alpha_kd_k$.

• Если $ \ left \ | x_ {k + 1-x_k} \ right \ | <\ varepsilon_1 $или$ \ left \ | \ bigtriangledown f \ left (x_ {k + 1} \ right) \ right \ | \ leq \ varepsilon_2 $, перейдите к шагу 6, в противном случае установите$ k = k + 1 $ и перейдите к шагу 2.

• Оптимальным решением является $\ hat {x} = x_ {k + 1}$.

Инициализируйте $x_0$, $\ varepsilon_1$, $\ varepsilon_2$ и установите $k = 0$.

Установите $d_k = - \ bigtriangledown f \ left (x_k \ right)$ или $d_k = - \ frac {\ bigtriangledown f \ left (x_k \ right)} {\ left \ | \ bigtriangledown f \ left (x_k \ right) \ right \ |}$.

найдите $\ alpha_k$ таким образом, чтобы минимизировать $\ phi \ left (\ alpha \ right) = f \ left (x_k + \ alpha d_k \ right)$.

Установите $x_ {k + 1} = x_k + \ alpha_kd_k$.

Если $ \ left \ | x_ {k + 1-x_k} \ right \ | <\ varepsilon_1 $или$ \ left \ | \ bigtriangledown f \ left (x_ {k + 1} \ right) \ right \ | \ leq \ varepsilon_2 $, перейдите к шагу 6, в противном случае установите$ k = k + 1 $ и перейдите к шагу 2.

Оптимальным решением является $\ hat {x} = x_ {k + 1}$.

Метод Ньютона

Метод Ньютона работает по следующему принципу —

$f \ left (x \ right) = y \ left (x \ right) = f \ left (x_k \ right) + \ left (x-x_k \ right) ^ T \ bigtriangledown f \ left (x_k \ right) + \ frac {1} {2} \ left (x-x_k \ right) ^ TH \ left (x_k \ right) \ left (x-x_k \ right)$

$\ bigtriangledown y \ left (x \ right) = \ bigtriangledown f \ left (x_k \ right) + H \ left (x_k \ right) \ left (x-x_k \ right)$

При $x_ {k + 1}, \ bigtriangledown y \ left (x_ {k + 1} \ right) = \ bigtriangledown f \ left (x_k \ right) + H \ left (x_k \ right) \ left (x_ {k +1} -x_k \ right)$

Для $x_ {k + 1}$ быть оптимальным решением $\ bigtriangledown y \ left (x_k + 1 \ right) = 0$

Таким образом, $x_ {k + 1} = x_k-H \ left (x_k \ right) ^ {- 1} \ bigtriangledown f \ left (x_k \ right)$

Здесь $H \ left (x_k \ right)$ должен быть неособым.

Следовательно, алгоритм выглядит следующим образом:

Шаг 1 — Инициализируйте $x_0, \ varepsilon$ и установите $k = 0$.

Шаг 2 — найдите $H \ left (x_k \ right) \ bigtriangledown f \ left (x_k \ right)$.

Шаг 3 — Решите для линейной системы $H \ left (x_k \ right) h \ left (x_k \ right) = \ bigtriangledown f \ left (x_k \ right)$ для $h \ left (x_k \ right)$.

Шаг 4 — найдите $x_ {k + 1} = x_k-h \ left (x_k \ right)$.

Шаг 5 — Если $ \ left \ | x_ {k + 1} -x_k \ right \ | <\ varepsilon $или$ \ left \ | \ bigtriangledown f \ left (x_k \ right) \ right \ | \ leq \ varepsilon $, затем перейдите к шагу 6, в противном случае установите$ k = k + 1 $ и перейдите к шагу 2.

Шаг 6 — Оптимальным решением является $\ hat {x} = x_ {k + 1}$.

Метод сопряженных градиентов

Этот метод используется для решения задач следующих типов —

$min f \ left (x \ right) = \ frac {1} {2} x ^ T Qx-bx$

где Q — положительно определенная матрица nXn, а b — постоянная.

Учитывая $x_0, \ varepsilon,$ compute $g_0 = Qx_0-b$

Установите $d_0 = -g_0$ для $k = 0,1,2, ...,$

Установить $\ alpha_k = \ frac {g_ {k} ^ {T} g_k} {d_ {k} ^ {T} Q d_k}$

Вычислить $x_ {k + 1} = x_k + \ alpha_kd_k$

Установите $g_ {k + 1} = g_k + \ alpha_kd_k$

Вычислить $\ beta_k = \ frac {g_ {k} ^ {T} g_k} {d_ {k} ^ {T} Qd_k}$

Вычислить $x_ {k + 1} = x_k + \ alpha_kd_k$

Установите $g_ {k + 1} = x_k + \ alpha_kQd_k$

Вычислить $\ beta_k = \ frac {g_ {k + 1} ^ {T} g_ {k + 1}} {g_ {k} ^ {T} gk}$

Установите $d_ {k + 1} = - g_ {k + 1} + \ beta_kd_k$.