Процесс извлечения исходного сигнала сообщения из волны SSBSC известен как обнаружение или демодуляция SSBSC. Когерентный детектор используется для демодуляции волны SSBSC.
Когерентный детектор
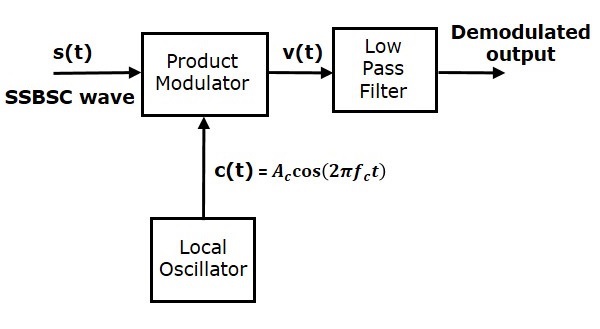
Здесь тот же самый сигнал несущей (который используется для генерации волны SSBSC) используется для обнаружения сигнала сообщения. Следовательно, этот процесс обнаружения называется когерентным или синхронным обнаружением . Ниже приведена блок-схема когерентного детектора.
В этом процессе сигнал сообщения может быть извлечен из волны SSBSC путем умножения его на несущую, имеющую ту же частоту и фазу несущей, которые используются в модуляции SSBSC. Полученный сигнал затем пропускается через фильтр нижних частот. Выход этого фильтра — желаемый сигнал сообщения.
Рассмотрим следующую волну SSBSC, имеющую нижнюю боковую полосу .
$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $$
Выход гетеродина
$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$
Из рисунка мы можем записать вывод модулятора продукта как
$$ v \ left (t \ right) = s \ left (t \ right) c \ left (t \ right) $$
Подставьте значения $ s \ left (t \ right) $ и $ c \ left (t \ right) $ в вышеприведенном уравнении.
$$ v \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] A_c \ cos \ left (2 \ pi f_ct \ право) $$
$ = \ frac {A_m {A_ {c}} ^ {2}} {2} \ cos \ left [2 \ pi \ left (f_c -f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ право) $
$ = \ frac {A_m {A_ {c}} ^ {2}} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c-fm \ right) \ right] + \ cos \ left ( 2 \ pi f_m \ right) t \ right \} $
$ v \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) + \ frac {A_m {A_ {c} } ^ {2}} {4} \ cos \ left [2 \ pi \ left (2f_c-f_m \ right) t \ right] $
В приведенном выше уравнении первый член — это масштабированная версия сигнала сообщения. Его можно извлечь, пропустив вышеуказанный сигнал через фильтр нижних частот.
Следовательно, выходной сигнал фильтра нижних частот
$$ v_0 \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) $$
Здесь коэффициент масштабирования составляет $ \ frac {{A_ {c}} ^ {2}} {4} $.
Мы можем использовать ту же блок-схему для демодуляции волны SSBSC, имеющей верхнюю боковую полосу. Рассмотрим следующую волну SSBSC, имеющую верхнюю боковую полосу .
$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $$
Выход гетеродина
$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$
Мы можем записать вывод модулятора продукта как
$$ v \ left (t \ right) = s \ left (t \ right) c \ left (t \ right) $$
Подставьте значения $ s \ left (t \ right) $ и $ c \ left (t \ right) $ в вышеприведенном уравнении.
$$ \ Rightarrow v \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] A_c \ cos \ left (2 \ pi f_ct \ right) $$
$ = \ frac {A_m {A_ {c}} ^ {2}} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ право) $
$ = \ frac {A_m {A_ {c}} ^ {2}} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c + f_m \ right) t \ right] + \ cos \ left (2 \ pi f_mt \ right) \ right \} $
$ v \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) + \ frac {A_m {A_ {c} } ^ {2}} {4} \ cos \ left [2 \ pi \ left (2f_c + f_m \ right) t \ right] $
В приведенном выше уравнении первый член — это масштабированная версия сигнала сообщения. Его можно извлечь, пропустив вышеуказанный сигнал через фильтр нижних частот.
Следовательно, выходной сигнал фильтра нижних частот
$$ v_0 \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) $$
Здесь также коэффициент масштабирования составляет $ \ frac {{A_ {c}} ^ {2}} {4} $.
Следовательно, мы получаем одинаковый демодулированный выход в обоих случаях с помощью когерентного детектора.