Аналоговая связь — AM модуляторы

В этой главе мы поговорим о модуляторах, которые генерируют амплитудно-модулированную волну. Следующие два модулятора генерируют АМ волну.

• Квадратный закон модулятора
• Переключающий модулятор

Квадратный Закон Модулятор

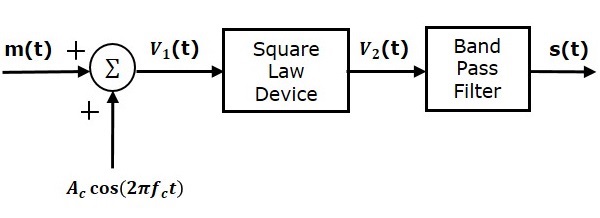
Ниже приведена блок-схема квадратичного модулятора

Пусть модулирующие и несущие сигналы обозначаются как $m \ left (t \ right)$ и $A \ cos \ left (2 \ pi f_ct \ right)$ соответственно. Эти два сигнала применяются в качестве входных данных для блока летнего (сумматора). Этот летний блок выдает выходной сигнал, который является сложением модулирующего и несущего сигналов. Математически мы можем записать это как

$$V_1t = m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right)$$

Этот сигнал $V_1t$ подается на вход нелинейного устройства, такого как диод. Характеристики диода тесно связаны с квадратичным законом.

$V_2t = k_1V_1 \ left (t \ right) + k_2V_1 ^ 2 \ left (t \ right)$ (уравнение 1)

Где $k_1$ и $k_2$ — постоянные.

Замените $V_1 \ left (t \ right)$ в уравнении 1

$$V_2 \ left (t \ right) = k_1 \ left [m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) \ right] + k_2 \ left [m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) \ right] ^ 2$$

$\ Rightarrow V_2 \ left (t \ right) = k_1 m \ left (t \ right) + k_1 A_c \ cos \ left (2 \ pi f_ct \ right) + k_2 m ^ 2 \ left (t \ right) +$

$k_2A_c ^ 2 \ cos ^ 2 \ left (2 \ pi f_ct \ right) + 2k_2m \ left (t \ right) A_c \ cos \ left (2 \ pi f_ct \ right)$

$\ Rightarrow V_2 \ left (t \ right) = k_1 m \ left (t \ right) + k_2 m ^ 2 \ left (t \ right) + k_2 A ^ 2_c \ cos ^ 2 \ left (2 \ pi f_ct \ справа) +$

$k_1A_c \ left [1+ \ left (\ frac {2k_2} {k_1} \ right) m \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$

Последний член вышеприведенного уравнения представляет желаемую волну AM, а первые три члена вышеприведенного уравнения являются нежелательными. Итак, с помощью полосового фильтра мы можем пропустить только АМ волну и исключить первые три члена.

Следовательно, на выходе квадратичного модулятора

$$s \ left (t \ right) = k_1A_c \ left [1+ \ left (\ frac {2k_2} {k_1} \ right) m \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$$

Стандартное уравнение AM-волны

$$s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$$

Где $K_a$ — амплитудная чувствительность

Сравнивая выходные данные квадратичного модулятора со стандартным уравнением AM-волны, мы получим коэффициент масштабирования как $k_1$ и амплитудную чувствительность $k_a$ как $\ frac {2k_2} {k1}$.

Модулятор переключения

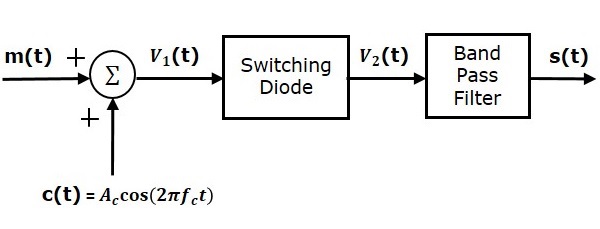
Ниже приведена блок-схема переключения модулятора.

Переключающий модулятор похож на квадратичный модулятор. Единственное отличие состоит в том, что в квадратичном модуляторе диод работает в нелинейном режиме, тогда как в переключающем модуляторе диод должен работать как идеальный переключатель.

Пусть модулирующие и несущие сигналы обозначаются как $m \ left (t \ right)$ и $c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right)$ соответственно. Эти два сигнала применяются в качестве входных данных для блока летнего (сумматора). Летний блок выдает выходной сигнал, который является сложением модулирующих и несущих сигналов. Математически мы можем записать это как

$$V_1 \ left (t \ right) = m \ left (t \ right) + c \ left (t \ right) = m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) )$$

Этот сигнал $V_1 \ left (t \ right)$ применяется как вход диода. Предположим, что величина модулирующего сигнала очень мала по сравнению с амплитудой несущего сигнала $A_c$. Таким образом, действие включения и выключения диода контролируется сигналом несущей $c \ left (t \ right)$. Это означает, что диод будет смещен в прямом направлении, когда $c \ left (t \ right)> 0$, и будет смещен в обратном направлении, когда $c \ left (t \ right) <0$.

Следовательно, выход диода

$$V_2 \ left (t \ right) = \ left \ {\ begin {matrix} V_1 \ left (t \ right) & if & c \ left (t \ right)> 0 \\ 0 & if & c \ left (t \ right) <0 \ end {matrix} \ right.$$

Мы можем приблизить это как

$V_2 \ left (t \ right) = V_1 \ left (t \ right) x \ left (t \ right)$ (уравнение 2)

Где $x \ left (t \ right)$ — периодическая последовательность импульсов с периодом времени $T = \ frac {1} {f_c}$

Представление этой периодической последовательности импульсов в рядах Фурье

$$x \ left (t \ right) = \ frac {1} {2} + \ frac {2} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ справа) ^ n-1} {2n-1} \ cos \ left (2 \ pi \ left (2n-1 \ right) f_ct \ right)$$

$$\ Rightarrow x \ left (t \ right) = \ frac {1} {2} + \ frac {2} {\ pi} \ cos \ left (2 \ pi f_ct \ right) - \ frac {2} { 3 \ pi} \ cos \ left (6 \ pi f_ct \ right) + ....$$

Подставьте значения $V_1 \ left (t \ right)$ и $x \ left (t \ right)$ в уравнение 2.

$V_2 \ left (t \ right) = \ left [m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) \ right] \ left [\ frac {1} {2} + \ frac {2} {\ pi} \ cos \ left (2 \ pi f_ct \ right) - \ frac {2} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) + ..... \ right]$

$V_2 \ left (t \ right) = \ frac {m \ left (t \ right)} {2} + \ frac {A_c} {2} \ cos \ left (2 \ pi f_ct \ right) + \ frac { 2m \ left (t \ right)} {\ pi} \ cos \ left (2 \ pi f_ct \ right) + \ frac {2A_c} {\ pi} \ cos ^ 2 \ left (2 \ pi f_ct \ right) -$

$\ frac {2m \ left (t \ right)} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) - \ frac {2A_c} {3 \ pi} \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (6 \ pi f_ct \ right) + .....$

$V_2 \ left (t \ right) = \ frac {A_c} {2} \ left (1+ \ left (\ frac {4} {\ pi A_c} \ right) m \ left (t \ right) \ right) \ cos \ left (2 \ pi f_ct \ right) + \ frac {m \ left (t \ right)} {2} + \ frac {2A_c} {\ pi} \ cos ^ 2 \ left (2 \ pi f_ct \ правильно) -$

$\ frac {2m \ left (t \ right)} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) - \ frac {2A_c} {3 \ pi} \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (6 \ pi f_ct \ right) + .....$

1- ^й член приведенного выше уравнения представляет желаемую AM-волну, а остальные члены являются нежелательными. Таким образом, с помощью полосового фильтра мы можем пропустить только АМ волну и исключить оставшиеся члены.

Следовательно, выход модулятора переключения

$$s \ left (t \ right) = \ frac {A_c} {2} \ left (1+ \ left (\ frac {4} {\ pi A_c} \ right) m \ left (t \ right) \ right ) \ cos \ left (2 \ pi f_ct \ right)$$

Мы знаем, что стандартное уравнение AM волны

$$s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$$

Где $k_a$ — амплитудная чувствительность.

Сравнивая выходной сигнал переключающего модулятора со стандартным уравнением АМ волны, мы получим масштабный коэффициент как 0,5 и амплитудную чувствительность $k_a$ как $\ frac {4} {\ pi A_c}$.