Амплитудная модуляция

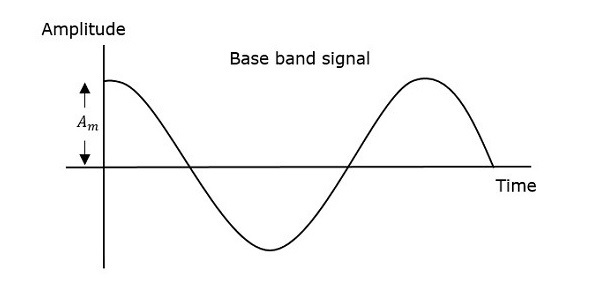
Непрерывная волна идет непрерывно без каких-либо интервалов, и это сигнал сообщения основной полосы частот, который содержит информацию. Эта волна должна быть модулирована.

Согласно стандартному определению, «амплитуда несущего сигнала изменяется в соответствии с мгновенной амплитудой модулирующего сигнала». Это означает, что амплитуда несущего сигнала, не содержащего информацию, изменяется в соответствии с амплитудой сигнала, содержащего информацию, при каждое мгновение Это можно хорошо объяснить следующими рисунками.

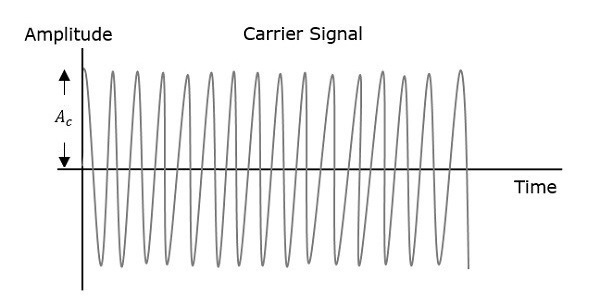
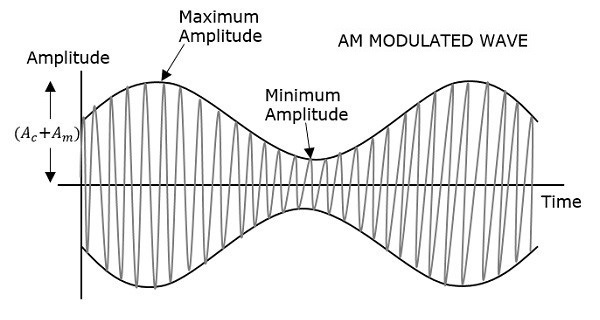
На первом рисунке показана модулирующая волна, которая является сигналом сообщения. Следующей является несущая волна, которая является высокочастотным сигналом и не содержит никакой информации. В то время как последний является результирующей модулированной волной.

Можно наблюдать, что положительные и отрицательные пики несущей волны взаимосвязаны с воображаемой линией. Эта линия помогает воссоздать точную форму модулирующего сигнала. Эта воображаемая линия на несущей волне называется огибающей . Это то же самое, что и сигнал сообщения.

Математические выражения

Ниже приведены математические выражения для этих волн.

Представление волн во временной области

Пусть модулирующий сигнал будет,

$$m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right)$$

и сигнал несущей будет,

$$c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right)$$

Куда,

$A_m$ и $A_c$ являются амплитудой модулирующего сигнала и сигнала несущей соответственно.

$f_m$ и $f_c$ являются частотой модулирующего сигнала и сигнала несущей соответственно.

Тогда уравнение амплитудно-модулированной волны будет

$s (t) = \ left [A_c + A_m \ cos \ left (2 \ pi f_mt \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$ (уравнение 1)

Индекс модуляции

Несущая волна, после модуляции, если вычисляется модулированный уровень, то такая попытка называется индексом модуляции или глубиной модуляции . Он устанавливает уровень модуляции, которому подвергается несущая волна.

Переставьте уравнение 1, как показано ниже.

$s (t) = A_c \ left [1+ \ left (\ frac {A_m} {A_c} \ right) \ cos \ left (2 \ pi f_mt \ right) \ right] \ cos \ left (2 \ pi f_ct \ право)$

$\ Rightarrow s \ left (t \ right) = A_c \ left [1 + \ mu \ cos \ left (2 \ pi f_m t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$ ( Уравнение 2)

Где $\ mu$ — индекс модуляции, и он равен отношению $A_m$ и $A_c$. Математически мы можем записать это как

$\ mu = \ frac {A_m} {A_c}$ (уравнение 3)

Следовательно, мы можем вычислить значение индекса модуляции, используя вышеприведенную формулу, когда амплитуды сигналов сообщения и несущей известны.

Теперь, давайте выведем еще одну формулу для индекса модуляции, рассматривая уравнение 1. Мы можем использовать эту формулу для вычисления значения индекса модуляции, когда известны максимальная и минимальная амплитуды модулированной волны.

Пусть $A_ \ max$ и $A_ \ min$ — максимальные и минимальные амплитуды модулированной волны.

Мы получим максимальную амплитуду модулированной волны, когда $\ cos \ left (2 \ pi f_mt \ right)$ равно 1.

$\ Rightarrow A_ \ max = A_c + A_m$ (уравнение 4)

Мы получим минимальную амплитуду модулированной волны, когда $\ cos \ left (2 \ pi f_mt \ right)$ равно -1.

$\ Rightarrow A_ \ min = A_c - A_m$ (уравнение 5)

Добавить уравнение 4 и уравнение 5.

$$A_ \ max + A_ \ min = A_c + A_m + A_c-A_m = 2A_c$$

$\ Rightarrow A_c = \ frac {A_ \ max + A_ \ min} {2}$ (Уравнение 6)

Вычтите уравнение 5 из уравнения 4.

$$A_ \ max - A_ \ min = A_c + A_m - \ left (A_c -A_m \ right) = 2A_m$$

$\ Rightarrow A_m = \ frac {A_ \ max - A_ \ min} {2}$ (уравнение 7)

Соотношение уравнения 7 и уравнения 6 будет следующим.

$$\ frac {A_m} {A_c} = \ frac {\ left (A_ {max} - A_ {min} \ right) / 2} {\ left (A_ {max} + A_ {min} \ right) / 2 }$$

$\ Rightarrow \ mu = \ frac {A_ \ max - A_ \ min} {A_ \ max + A_ \ min}$ (уравнение 8)

Следовательно, уравнение 3 и уравнение 8 являются двумя формулами для индекса модуляции. Индекс модуляции или глубина модуляции часто обозначаются в процентах, называемых процентами модуляции. Мы получим процент модуляции , просто умножив значение индекса модуляции на 100.

Для идеальной модуляции значение индекса модуляции должно быть 1, что означает, что процент модуляции должен составлять 100%.

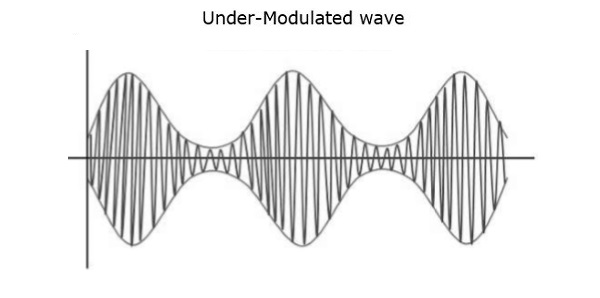
Например, если это значение меньше 1, т. Е. Индекс модуляции равен 0,5, то модулированный выходной сигнал будет выглядеть следующим образом. Это называется недомодуляцией . Такая волна называется немодулированной волной .

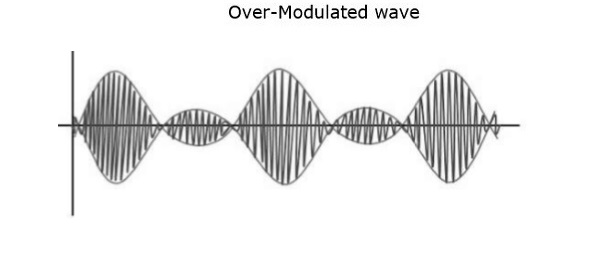
Если значение индекса модуляции больше 1, т. Е. 1,5 или около того, то волна будет перемодулированной волной . Это будет выглядеть следующим образом.

Когда значение индекса модуляции увеличивается, несущая испытывает изменение фазы на 180 ^o , что вызывает дополнительные боковые полосы и, следовательно, волна искажается. Такая перемодулированная волна вызывает помехи, которые невозможно устранить.

Пропускная способность AM Wave

Ширина полосы (BW) — это разница между самой высокой и самой низкой частотами сигнала. Математически мы можем записать это как

$$BW = f_ {max} - f_ {min}$$

Рассмотрим следующее уравнение амплитудно-модулированной волны.

$$s \ left (t \ right) = A_c \ left [1 + \ mu \ cos \ left (2 \ pi f_m t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$$

$$\ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_c \ mu \ cos (2 \ pi f_ct) \ cos \ left (2 \ pi f_mt \ right)$$

$\ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c + f_m) \ right) t \ right] + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right]$

Следовательно, амплитуда модулированной волны имеет три частоты. Это несущая частота $f_c$, частота верхней боковой полосы $f_c + f_m$ и частота нижней боковой полосы $f_c-f_m$

Вот,

$f_ {max} = f_c + f_m$ и $f_ {min} = f_c-f_m$

Подставьте значения $f_ {max}$ и $f_ {min}$ в формулу пропускной способности.

$$BW = f_c + f_m- \ left (f_c-f_m \ right)$$

$$\ Rightarrow BW = 2f_m$$

Таким образом, можно сказать, что ширина полосы, требуемая для амплитудно-модулированной волны, в два раза превышает частоту модулирующего сигнала.

Расчеты мощности AM Wave

Рассмотрим следующее уравнение амплитудно-модулированной волны.

$\ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \) справа) t \ right] + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right]$

Мощность AM-волны равна сумме мощностей несущей, частотной составляющей верхней боковой полосы и нижней боковой полосы.

$$p_t = P_c + Р- {USB} + Р- {LSB}$$

Мы знаем, что стандартная формула для мощности сигнала cos

$$P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m / \ sqrt {2} \ right) ^ 2} {2}$$

Куда,

$v_ {rms}$ — среднеквадратичное значение сигнала cos.

$v_m$ — пиковое значение сигнала cos.

Во-первых, давайте найдем мощности несущей, верхней и нижней боковой полосы одну за другой.

Мощность несущей

$$P_c = \ frac {\ left (A_c / \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {c}} ^ {2}} {2R}$$

Мощность верхней боковой полосы

PUSB= frac left(Ac mu/2 sqrt2 right)2R= fracAc2 mu28R $$P_ {USB} = \ frac {\ left (A_c \ mu / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R}$$

Точно так же мы получим мощность нижней боковой полосы такую ​​же, как и мощность верхней боковой полосы.

PLSB= fracAc2 mu28R $$P_ {LSB} = \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R}$$

Теперь давайте добавим эти три силы, чтобы получить мощность волны AM.

Pt= fracAc22R+ fracAc2 mu28R+ fracAc2 mu28R $$P_t = \ frac {{A_ {c}} ^ {2}} {2R} + \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} + \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R}$$

$$\ Rightarrow P_t = \ left (\ frac {{A_ {c}} ^ {2}} {2R} \ right) \ left (1+ \ frac {\ mu ^ 2} {4} + \ frac {\ mu ^ 2} {4} \ right)$$

$$\ Rightarrow P_t = P_c \ left (1+ \ frac {\ mu ^ 2} {2} \ right)$$

Мы можем использовать приведенную выше формулу для расчета мощности АМ-волны, когда мощность несущей и индекс модуляции известны.

Если индекс модуляции $\ mu = 1$, то мощность волны АМ в 1,5 раза превышает мощность несущей. Таким образом, мощность, необходимая для передачи АМ-волны, в 1,5 раза превышает мощность несущей для идеальной модуляции.