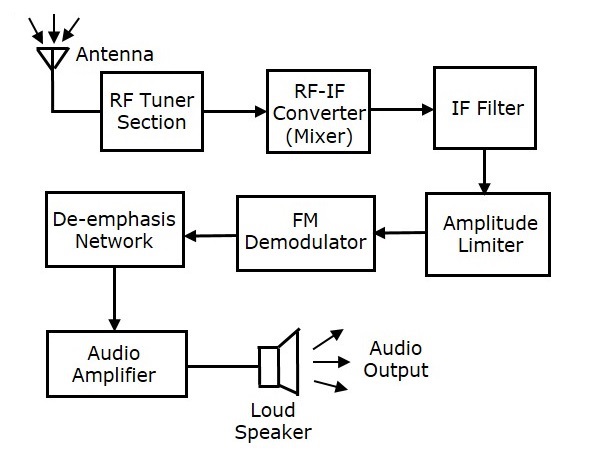
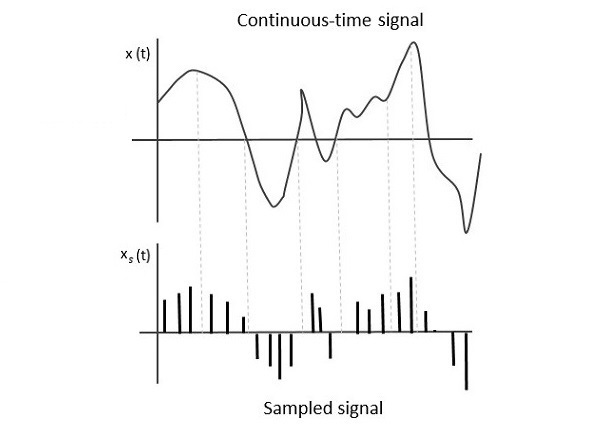
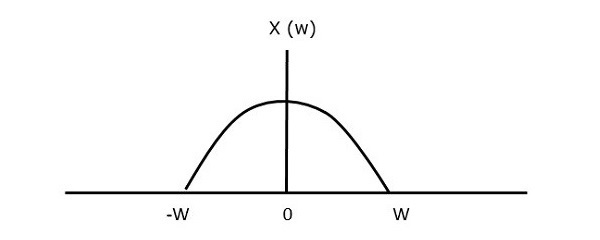
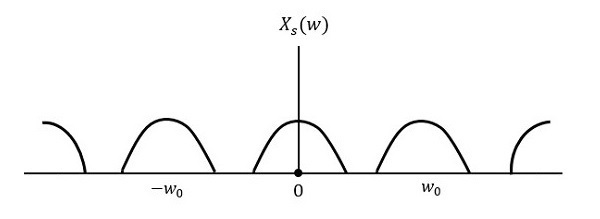
Аналоговая связь — Введение

Слово «общение» происходит от латинского слова commūnicāre, что означает «делиться». Коммуникация является основным шагом для обмена информацией.

Например, ребенок в колыбели общается с плачем, когда ей нужна мама. Корова громко кричит, когда она в опасности. Человек общается с помощью языка. Общение — это мост, которым нужно делиться.

Общение может быть определено как процесс обмена информацией с помощью таких средств, как слова, действия, знаки и т. Д., Между двумя или более лицами.

Части системы связи

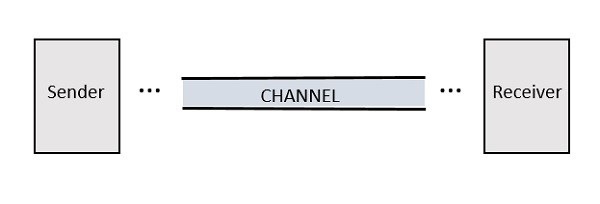
Любая система, которая обеспечивает связь, состоит из трех важных и основных частей, как показано на следующем рисунке.

• Отправитель — это человек, который отправляет сообщение. Это может быть передающая станция, с которой передается сигнал.

• Канал — это среда, по которой сигналы сообщения проходят до места назначения.

• Получатель — это человек, который получает сообщение. Это может быть приемная станция, где принимается передаваемый сигнал.

Отправитель — это человек, который отправляет сообщение. Это может быть передающая станция, с которой передается сигнал.

Канал — это среда, по которой сигналы сообщения проходят до места назначения.

Получатель — это человек, который получает сообщение. Это может быть приемная станция, где принимается передаваемый сигнал.

Типы сигналов

Передача информации некоторыми средствами, такими как жесты, звуки, действия и т. Д., Может быть названа сигналом . Следовательно, сигнал может быть источником энергии, который передает некоторую информацию. Этот сигнал помогает установить связь между отправителем и получателем.

Электрический импульс или электромагнитная волна, которая проходит расстояние для передачи сообщения, может быть названа сигналом в системах связи.

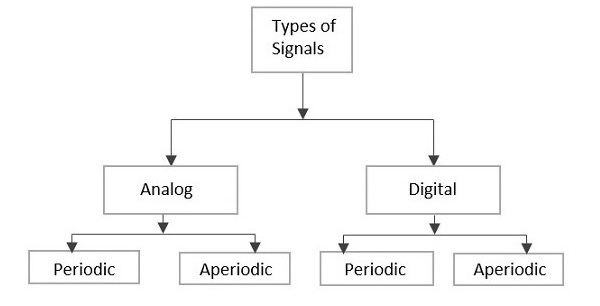
В зависимости от своих характеристик сигналы в основном подразделяются на два типа: аналоговые и цифровые. Аналоговые и цифровые сигналы дополнительно классифицируются, как показано на следующем рисунке.

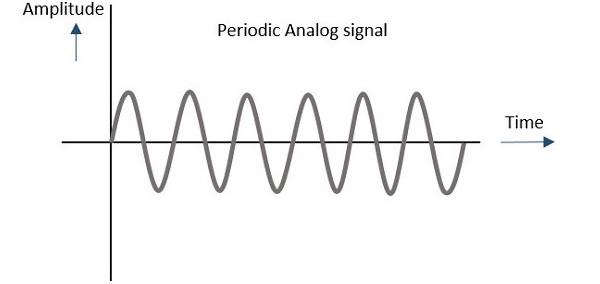
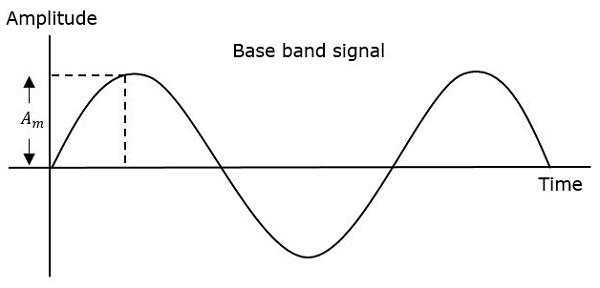
Аналоговый сигнал

Непрерывный изменяющийся во времени сигнал, который представляет изменяющуюся во времени величину, можно назвать аналоговым сигналом . Этот сигнал продолжает изменяться во времени в соответствии с мгновенными значениями величины, которая его представляет.

пример

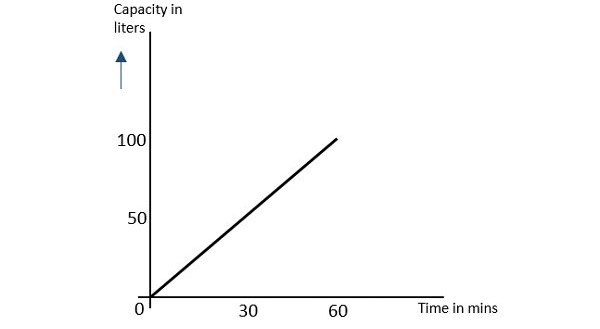
Давайте рассмотрим кран, который заполняет бак емкостью 100 литров в час (с 6 утра до 7 утра). Часть заполнения бака варьируется в зависимости от времени. Это означает, что через 15 минут (6:15 утра) четвертая часть бака заполняется, тогда как в 6:45 утра заполняется 3/4 бака.

Если мы попытаемся нанести на график различные порции воды в резервуаре в соответствии с изменяющимся временем, это будет выглядеть следующим образом.

Поскольку результат, показанный на этом изображении, изменяется (увеличивается) в зависимости от времени, эту изменяющуюся во времени величину можно понимать как Аналоговую величину. Сигнал, который представляет это условие с помощью наклонной линии на рисунке, является аналоговым сигналом . Связь, основанная на аналоговых сигналах и аналоговых значениях, называется аналоговой связью .

Цифровой сигнал

Сигнал, который является дискретным по природе или который не является непрерывным по форме, можно назвать цифровым сигналом . Этот сигнал имеет отдельные значения, обозначенные отдельно, которые не основаны на предыдущих значениях, как если бы они были получены в этот конкретный момент времени.

пример

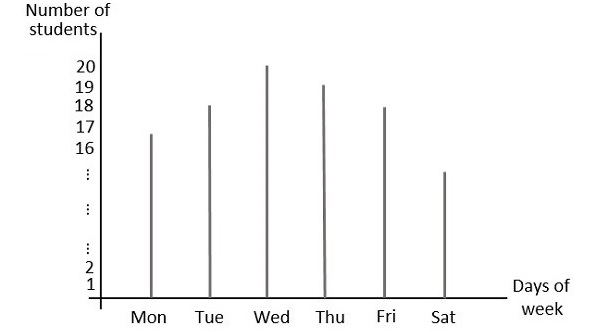
Давайте рассмотрим класс с 20 учениками. Если их посещаемость в неделю строится, это будет выглядеть следующим образом.

На этом рисунке значения указаны отдельно. Например, посещаемость класса в среду составляет 20, тогда как в субботу — 15. Эти значения можно рассматривать индивидуально и раздельно или дискретно, поэтому они называются дискретными значениями .

Двоичные цифры, которые имеют только 1 и 0, в основном называются цифровыми значениями . Следовательно, сигналы, которые представляют 1 и 0, также называются цифровыми сигналами . Связь, основанная на цифровых сигналах и цифровых значениях, называется цифровой связью.

Периодический сигнал

Любой аналоговый или цифровой сигнал, который повторяет свою схему в течение определенного периода времени, называется периодическим сигналом . Этот сигнал постоянно повторяется, и его легко предположить или рассчитать.

пример

Если мы рассмотрим машины в отрасли, процесс, который происходит один за другим, является непрерывной процедурой. Например, заготовка и сортировка сырья, обработка материала партиями, упаковка продуктов один за другим и т. Д. Повторяют определенную процедуру несколько раз.

Такой процесс, будь то аналоговый или цифровой, может быть графически представлен следующим образом.

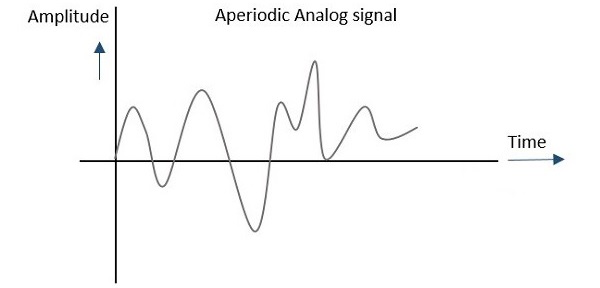
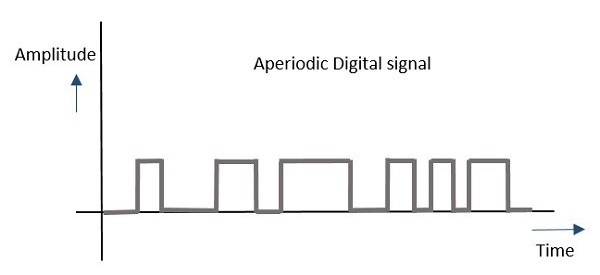
Апериодический сигнал

Любой аналоговый или цифровой сигнал, который не повторяет своего паттерна в течение определенного периода времени, называется апериодическим сигналом . Этот сигнал имеет свой паттерн продолженный, но паттерн не повторяется. Это также не так легко предположить или рассчитать.

пример

Повседневный распорядок дня человека, если рассматривать его, состоит из различных видов работы, которые занимают разные промежутки времени для разных задач. Временной интервал или работа не повторяются непрерывно. Например, человек не будет постоянно чистить зубы с утра до ночи, причем с одинаковым периодом времени.

Такой процесс, будь то аналоговый или цифровой, может быть графически представлен следующим образом.

В общем, сигналы, которые используются в системах связи, являются аналоговыми по своей природе, которые передаются в аналоговом виде или преобразуются в цифровые, а затем передаются в зависимости от требований.

Аналоговая связь — модуляция

Для передачи сигнала на расстояние, без влияния каких-либо внешних помех или добавления шума и без затухания, он должен пройти процесс, называемый модуляцией . Это улучшает силу сигнала без нарушения параметров исходного сигнала.

Что такое модуляция?

Сообщение, несущее сигнал, должно передаваться на расстояние, и для установления надежной связи ему требуется высокочастотный сигнал, который не должен влиять на исходные характеристики сигнала сообщения.

Характеристики сигнала сообщения, в случае изменения сообщения, содержащегося в нем, также изменяются. Следовательно, необходимо позаботиться о сигнале сообщения. Высокочастотный сигнал может распространяться на большие расстояния без воздействия внешних помех. Мы используем помощь такого высокочастотного сигнала, который называется сигналом несущей, для передачи сигнала нашего сообщения. Такой процесс называется просто модуляцией.

Модуляция — это процесс изменения параметров несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

Необходимость модуляции

Сигналы основной полосы частот несовместимы для прямой передачи. Для такого сигнала, чтобы преодолевать большие расстояния, его сила должна быть увеличена путем модуляции высокочастотной несущей, которая не влияет на параметры модулирующего сигнала.

Преимущества модуляции

Антенна, используемая для передачи, должна была быть очень большой, если модуляция не была введена. Диапазон связи ограничен, так как волна не может пройти расстояние без искажений.

Ниже приведены некоторые преимущества реализации модуляции в системах связи.

• Уменьшение размера антенны
• Нет смешивания сигналов
• Увеличение дальности связи
• Мультиплексирование сигналов
• Возможность регулировки пропускной способности
• Улучшенное качество приема

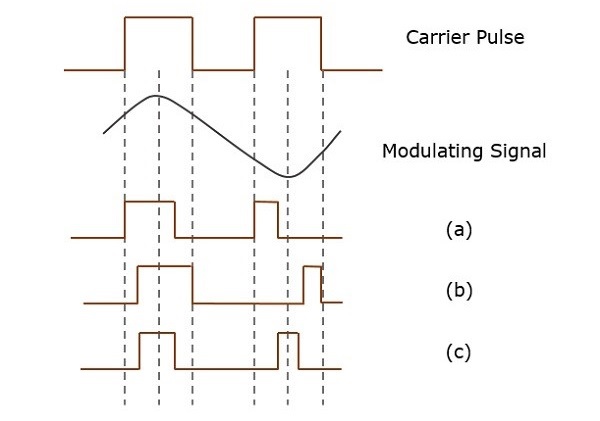
Сигналы в процессе модуляции

Ниже приведены три типа сигналов в процессе модуляции.

Сообщение или модулирующий сигнал

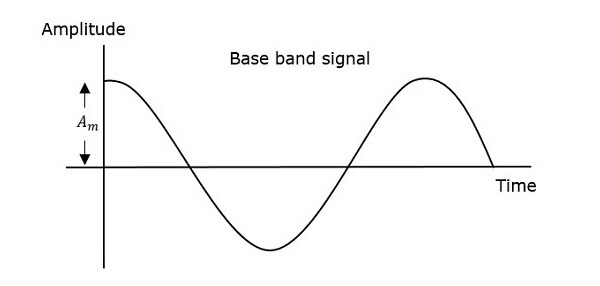
Сигнал, который содержит сообщение, подлежащее передаче, называется сигналом сообщения . Это сигнал основной полосы частот, который должен пройти процесс модуляции для передачи. Следовательно, он также называется модулирующим сигналом .

Сигнал несущей

Высокочастотный сигнал, который имеет определенную амплитуду, частоту и фазу, но не содержит информации, называется несущим сигналом . Это пустой сигнал и используется для передачи сигнала в приемник после модуляции.

Модулированный сигнал

Результирующий сигнал после процесса модуляции называется модулированным сигналом . Этот сигнал является комбинацией модулирующего сигнала и несущего сигнала.

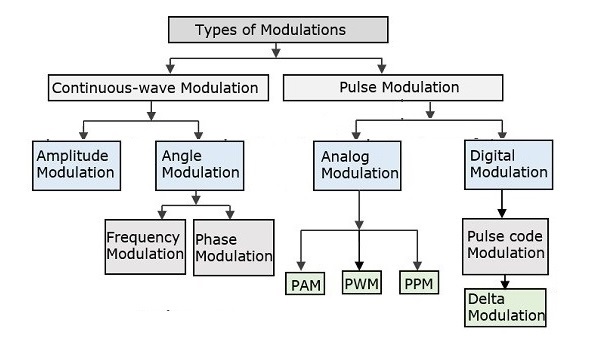
Типы модуляции

Существует много видов модуляции. В зависимости от используемых методов модуляции они классифицируются, как показано на следующем рисунке.

Типы модуляции в целом подразделяются на непрерывно-волновую модуляцию и импульсную модуляцию.

Непрерывно-волновая модуляция

При непрерывно-волновой модуляции высокочастотная синусоидальная волна используется в качестве несущей. Это далее разделено на амплитуду и угловую модуляцию.

• Если амплитуда высокочастотной несущей волны изменяется в соответствии с мгновенной амплитудой модулирующего сигнала, то такой метод называется амплитудной модуляцией .

• Если угол несущей волны изменяется в соответствии с мгновенным значением модулирующего сигнала, то такая методика называется угловой модуляцией . Угловая модуляция дополнительно делится на частотную модуляцию и фазовую модуляцию.

  • Если частота несущей волны изменяется в соответствии с мгновенным значением модулирующего сигнала, то такой метод называется частотной модуляцией .

  • Если фаза высокочастотной несущей волны изменяется в соответствии с мгновенным значением модулирующего сигнала, то такой метод называется фазовой модуляцией .

Если амплитуда высокочастотной несущей волны изменяется в соответствии с мгновенной амплитудой модулирующего сигнала, то такой метод называется амплитудной модуляцией .

Если угол несущей волны изменяется в соответствии с мгновенным значением модулирующего сигнала, то такая методика называется угловой модуляцией . Угловая модуляция дополнительно делится на частотную модуляцию и фазовую модуляцию.

Если частота несущей волны изменяется в соответствии с мгновенным значением модулирующего сигнала, то такой метод называется частотной модуляцией .

Если фаза высокочастотной несущей волны изменяется в соответствии с мгновенным значением модулирующего сигнала, то такой метод называется фазовой модуляцией .

Импульсная модуляция

В импульсной модуляции периодическая последовательность прямоугольных импульсов используется в качестве несущей волны. Это далее разделено на аналоговую и цифровую модуляцию.

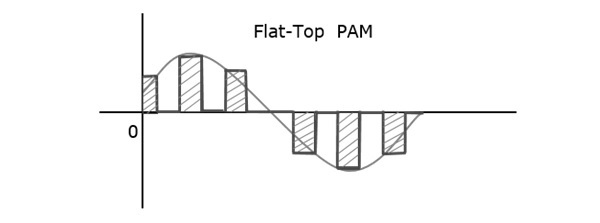
В методе аналоговой модуляции, если амплитуда, длительность или положение импульса изменяются в соответствии с мгновенными значениями модулирующего сигнала основной полосы частот, то такой метод называется импульсной амплитудной модуляцией (PAM) или импульсной длительностью / шириной модуляции (PDM). / PWM), или импульсная модуляция положения (PPM).

В цифровой модуляции используется метод модуляции с импульсной кодовой модуляцией (PCM), в котором аналоговый сигнал преобразуется в цифровую форму, состоящую из 1 и 0. Поскольку в результате получается последовательность закодированных импульсов, это называется PCM. Это далее развито как Дельта Модуляция (DM). Эти методы цифровой модуляции обсуждаются в нашем руководстве по цифровой связи.

Амплитудная модуляция

Непрерывная волна идет непрерывно без каких-либо интервалов, и это сигнал сообщения основной полосы частот, который содержит информацию. Эта волна должна быть модулирована.

Согласно стандартному определению, «амплитуда несущего сигнала изменяется в соответствии с мгновенной амплитудой модулирующего сигнала». Это означает, что амплитуда несущего сигнала, не содержащего информацию, изменяется в соответствии с амплитудой сигнала, содержащего информацию, при каждое мгновение Это можно хорошо объяснить следующими рисунками.

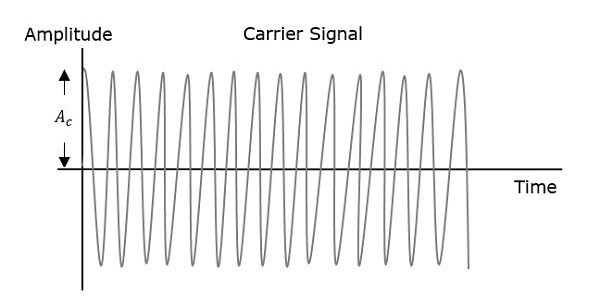
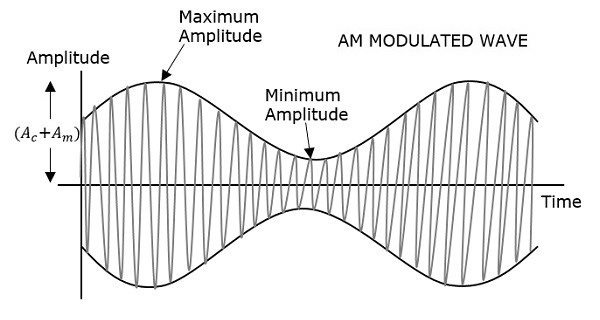
На первом рисунке показана модулирующая волна, которая является сигналом сообщения. Следующей является несущая волна, которая является высокочастотным сигналом и не содержит никакой информации. В то время как последний является результирующей модулированной волной.

Можно наблюдать, что положительные и отрицательные пики несущей волны взаимосвязаны с воображаемой линией. Эта линия помогает воссоздать точную форму модулирующего сигнала. Эта воображаемая линия на несущей волне называется огибающей . Это то же самое, что и сигнал сообщения.

Математические выражения

Ниже приведены математические выражения для этих волн.

Представление волн во временной области

Пусть модулирующий сигнал будет,

$$m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right)$$

и сигнал несущей будет,

$$c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right)$$

Куда,

$A_m$ и $A_c$ являются амплитудой модулирующего сигнала и сигнала несущей соответственно.

$f_m$ и $f_c$ являются частотой модулирующего сигнала и сигнала несущей соответственно.

Тогда уравнение амплитудно-модулированной волны будет

$s (t) = \ left [A_c + A_m \ cos \ left (2 \ pi f_mt \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$ (уравнение 1)

Индекс модуляции

Несущая волна, после модуляции, если вычисляется модулированный уровень, то такая попытка называется индексом модуляции или глубиной модуляции . Он устанавливает уровень модуляции, которому подвергается несущая волна.

Переставьте уравнение 1, как показано ниже.

$s (t) = A_c \ left [1+ \ left (\ frac {A_m} {A_c} \ right) \ cos \ left (2 \ pi f_mt \ right) \ right] \ cos \ left (2 \ pi f_ct \ право)$

$\ Rightarrow s \ left (t \ right) = A_c \ left [1 + \ mu \ cos \ left (2 \ pi f_m t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$ ( Уравнение 2)

Где $\ mu$ — индекс модуляции, и он равен отношению $A_m$ и $A_c$. Математически мы можем записать это как

$\ mu = \ frac {A_m} {A_c}$ (уравнение 3)

Следовательно, мы можем вычислить значение индекса модуляции, используя вышеприведенную формулу, когда амплитуды сигналов сообщения и несущей известны.

Теперь, давайте выведем еще одну формулу для индекса модуляции, рассматривая уравнение 1. Мы можем использовать эту формулу для вычисления значения индекса модуляции, когда известны максимальная и минимальная амплитуды модулированной волны.

Пусть $A_ \ max$ и $A_ \ min$ — максимальные и минимальные амплитуды модулированной волны.

Мы получим максимальную амплитуду модулированной волны, когда $\ cos \ left (2 \ pi f_mt \ right)$ равно 1.

$\ Rightarrow A_ \ max = A_c + A_m$ (уравнение 4)

Мы получим минимальную амплитуду модулированной волны, когда $\ cos \ left (2 \ pi f_mt \ right)$ равно -1.

$\ Rightarrow A_ \ min = A_c - A_m$ (уравнение 5)

Добавить уравнение 4 и уравнение 5.

$$A_ \ max + A_ \ min = A_c + A_m + A_c-A_m = 2A_c$$

$\ Rightarrow A_c = \ frac {A_ \ max + A_ \ min} {2}$ (Уравнение 6)

Вычтите уравнение 5 из уравнения 4.

$$A_ \ max - A_ \ min = A_c + A_m - \ left (A_c -A_m \ right) = 2A_m$$

$\ Rightarrow A_m = \ frac {A_ \ max - A_ \ min} {2}$ (уравнение 7)

Соотношение уравнения 7 и уравнения 6 будет следующим.

$$\ frac {A_m} {A_c} = \ frac {\ left (A_ {max} - A_ {min} \ right) / 2} {\ left (A_ {max} + A_ {min} \ right) / 2 }$$

$\ Rightarrow \ mu = \ frac {A_ \ max - A_ \ min} {A_ \ max + A_ \ min}$ (уравнение 8)

Следовательно, уравнение 3 и уравнение 8 являются двумя формулами для индекса модуляции. Индекс модуляции или глубина модуляции часто обозначаются в процентах, называемых процентами модуляции. Мы получим процент модуляции , просто умножив значение индекса модуляции на 100.

Для идеальной модуляции значение индекса модуляции должно быть 1, что означает, что процент модуляции должен составлять 100%.

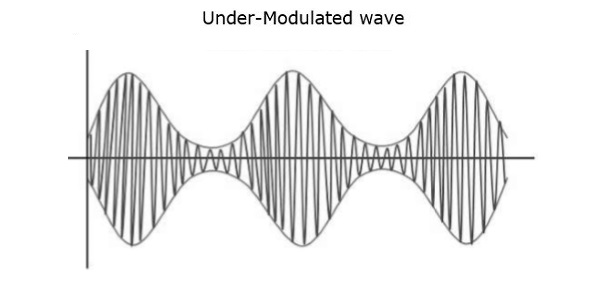
Например, если это значение меньше 1, т. Е. Индекс модуляции равен 0,5, то модулированный выходной сигнал будет выглядеть следующим образом. Это называется недомодуляцией . Такая волна называется немодулированной волной .

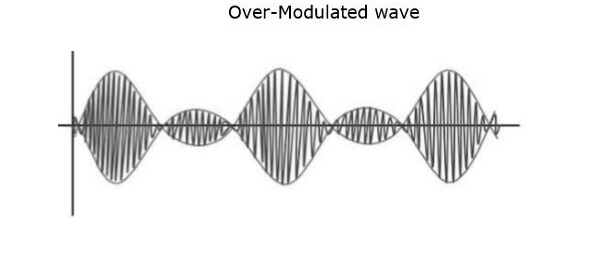
Если значение индекса модуляции больше 1, т. Е. 1,5 или около того, то волна будет перемодулированной волной . Это будет выглядеть следующим образом.

Когда значение индекса модуляции увеличивается, несущая испытывает изменение фазы на 180 ^o , что вызывает дополнительные боковые полосы и, следовательно, волна искажается. Такая перемодулированная волна вызывает помехи, которые невозможно устранить.

Пропускная способность AM Wave

Ширина полосы (BW) — это разница между самой высокой и самой низкой частотами сигнала. Математически мы можем записать это как

$$BW = f_ {max} - f_ {min}$$

Рассмотрим следующее уравнение амплитудно-модулированной волны.

$$s \ left (t \ right) = A_c \ left [1 + \ mu \ cos \ left (2 \ pi f_m t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$$

$$\ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_c \ mu \ cos (2 \ pi f_ct) \ cos \ left (2 \ pi f_mt \ right)$$

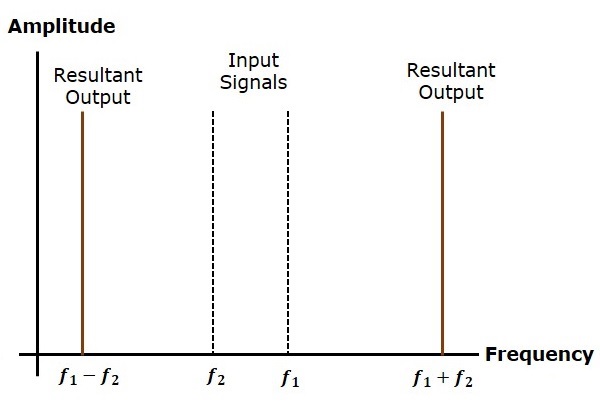
$\ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c + f_m) \ right) t \ right] + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right]$

Следовательно, амплитуда модулированной волны имеет три частоты. Это несущая частота $f_c$, частота верхней боковой полосы $f_c + f_m$ и частота нижней боковой полосы $f_c-f_m$

Вот,

$f_ {max} = f_c + f_m$ и $f_ {min} = f_c-f_m$

Подставьте значения $f_ {max}$ и $f_ {min}$ в формулу пропускной способности.

$$BW = f_c + f_m- \ left (f_c-f_m \ right)$$

$$\ Rightarrow BW = 2f_m$$

Таким образом, можно сказать, что ширина полосы, требуемая для амплитудно-модулированной волны, в два раза превышает частоту модулирующего сигнала.

Расчеты мощности AM Wave

Рассмотрим следующее уравнение амплитудно-модулированной волны.

$\ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \) справа) t \ right] + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right]$

Мощность AM-волны равна сумме мощностей несущей, частотной составляющей верхней боковой полосы и нижней боковой полосы.

$$p_t = P_c + Р- {USB} + Р- {LSB}$$

Мы знаем, что стандартная формула для мощности сигнала cos

$$P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m / \ sqrt {2} \ right) ^ 2} {2}$$

Куда,

$v_ {rms}$ — среднеквадратичное значение сигнала cos.

$v_m$ — пиковое значение сигнала cos.

Во-первых, давайте найдем мощности несущей, верхней и нижней боковой полосы одну за другой.

Мощность несущей

$$P_c = \ frac {\ left (A_c / \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {c}} ^ {2}} {2R}$$

Мощность верхней боковой полосы

$$P_ {USB} = \ frac {\ left (A_c \ mu / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R}$$

Точно так же мы получим мощность нижней боковой полосы такую ​​же, как и мощность верхней боковой полосы.

$$P_ {LSB} = \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R}$$

Теперь давайте добавим эти три силы, чтобы получить мощность волны AM.

$$P_t = \ frac {{A_ {c}} ^ {2}} {2R} + \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} + \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R}$$

$$\ Rightarrow P_t = \ left (\ frac {{A_ {c}} ^ {2}} {2R} \ right) \ left (1+ \ frac {\ mu ^ 2} {4} + \ frac {\ mu ^ 2} {4} \ right)$$

$$\ Rightarrow P_t = P_c \ left (1+ \ frac {\ mu ^ 2} {2} \ right)$$

Мы можем использовать приведенную выше формулу для расчета мощности АМ-волны, когда мощность несущей и индекс модуляции известны.

Если индекс модуляции $\ mu = 1$, то мощность волны АМ в 1,5 раза превышает мощность несущей. Таким образом, мощность, необходимая для передачи АМ-волны, в 1,5 раза превышает мощность несущей для идеальной модуляции.

Численные задачи 1

В предыдущей главе мы обсудили параметры, используемые в амплитудной модуляции. Каждый параметр имеет свою формулу. Используя эти формулы, мы можем найти соответствующие значения параметров. В этой главе давайте решим несколько проблем, основанных на концепции амплитудной модуляции.

Проблема 1

Модулирующий сигнал $m \ left (t \ right) = 10 \ cos \ left (2 \ pi \ times 10 ^ 3 t \ right)$ амплитудно модулируется несущим сигналом $c \ left (t \ right) = 50 \ cos \ left (2 \ pi \ times 10 ^ 5 т \ вправо)$. Найти индекс модуляции, мощность несущей и мощность, необходимую для передачи AM-волны.

Решение

Дано уравнение модулирующего сигнала как

$$m \ left (t \ right) = 10 \ cos \ left (2 \ pi \ times 10 ^ 3 t \ right)$$

Мы знаем стандартное уравнение модулирующего сигнала как

$$m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right)$$

Сравнивая два приведенных выше уравнения, получим

Амплитуда модулирующего сигнала как $A_m = 10 вольт$

и частота модулирующего сигнала как $$f_m = 10 ^ 3 Гц = 1 кГц$$

Учитывая, уравнение несущего сигнала

$$c \ left (t \ right) = 50 \ cos \ left (2 \ pi \ times 10 ^ 5t \ right)$$

Стандартное уравнение несущего сигнала

$$c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right)$$

Сравнивая эти два уравнения, мы получим

Амплитуда несущего сигнала в виде $A_c = 50 вольт$

и частота несущего сигнала как $f_c = 10 ^ 5 Гц = 100 кГц$

Мы знаем формулу для индекса модуляции как

$$\ mu = \ frac {A_m} {A_c}$$

Подставим значения $A_m$ и $A_c$ в приведенной выше формуле.

$$\ му = \ гидроразрыва {10} {50} = 0.2$$

Следовательно, значение индекса модуляции составляет 0,2, а процент модуляции составляет 20%.

Формула для мощности несущей $P_c =$ равна

$$P_c = \ гидроразрыва {{A_ {с}} ^ {2}} {2R}$$

Предположим, что $R = 1 \ Omega$ и подставим значение $A_c$ в приведенную выше формулу.

$$P_c = \ frac {\ left (50 \ right) ^ 2} {2 \ left (1 \ right)} = 1250 Вт$$

Следовательно, мощность несущей , $P_c$, составляет 1250 Вт .

Мы знаем, что формула для мощности, необходимой для передачи АМ волны, равна

$$\ Rightarrow P_t = P_c \ left (1+ \ frac {\ mu ^ 2} {2} \ right)$$

Подставим значения $P_c$ и $\ mu$ в приведенную выше формулу.

$$P_t = 1250 \ left (1+ \ frac {\ left (0.2 \ right) ^ 2} {2} \ right) = 1275W$$

Следовательно, мощность, необходимая для передачи AM- волны, составляет 1275 Вт .

Проблема 2

Уравнение амплитуды волны задается как $s \ left (t \ right) = 20 \ left [1 + 0,8 \ cos \ left (2 \ pi \ times 10 ^ 3t \ right) \ right] \ cos \ left (4 \ pi \ times 10 ^ 5t \ right)$. Найти мощность несущей, общую мощность боковой полосы и ширину полосы AM-волны.

Решение

Учитывая, уравнение амплитудно-модулированной волны

$$s \ left (t \ right) = 20 \ left [1 + 0,8 \ cos \ left (2 \ pi \ times 10 ^ 3t \ right) \ right] \ cos \ left (4 \ pi \ times 10 ^ 5t \ право)$$

Переписать приведенное выше уравнение как

$$s \ left (t \ right) = 20 \ left [1 + 0,8 \ cos \ left (2 \ pi \ times 10 ^ 3t \ right) \ right] \ cos \ left (2 \ pi \ times 2 \ times 10 ^ 5т \ справа)$$

Мы знаем, что уравнение амплитудно-модулированной волны

$$s \ left (t \ right) = A_c \ left [1+ \ mu \ cos \ left (2 \ pi f_mt \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$$

Сравнивая два приведенных выше уравнения, получим

Амплитуда несущего сигнала в виде $A_c = 20 вольт$

Индекс модуляции как $\ mu = 0,8$

Частота модулирующего сигнала как $f_m = 10 ^ 3 Гц = 1 КГц$

Частота несущего сигнала как $ f_c = 2 \ умноженная на 10 ^ 5 Гц = 200 кГц

Формула для мощности несущей $P_c$ равна

$$P_c = \ гидроразрыва {{A_ {е}} ^ {2}} {2R}$$

Предположим, что $R = 1 \ Omega$ и подставим значение $A_c$ в приведенную выше формулу.

$$P_c = \ frac {\ left (20 \ right) ^ 2} {2 \ left (1 \ right)} = 200 Вт$$

Следовательно, мощность несущей , $P_c$, составляет 200 Вт .

Мы знаем, что формула для общей мощности боковой полосы

$$Р- {SB} = \ {гидроразрыва P_c \ мю ^ 2} {2}$$

Подставим значения $P_c$ и $\ mu$ в приведенную выше формулу.

$$P_ {SB} = \ frac {200 \ times \ left (0.8 \ right) ^ 2} {2} = 64 Вт$$

Следовательно, общая мощность боковой полосы составляет 64 Вт.

Мы знаем формулу для пропускной способности AM-волны

$$BW = 2f_m$$

Замените значение $f_m$ в приведенной выше формуле.

$$BW = 2 \ left (1K \ right) = 2 КГц$$

Следовательно, полоса частот AM-волны составляет 2 кГц.

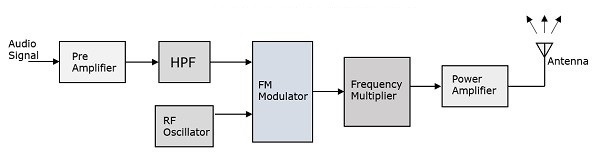
Аналоговая связь — AM модуляторы

В этой главе мы поговорим о модуляторах, которые генерируют амплитудно-модулированную волну. Следующие два модулятора генерируют АМ волну.

• Квадратный закон модулятора
• Переключающий модулятор

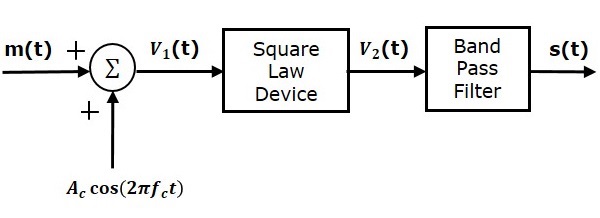
Квадратный Закон Модулятор

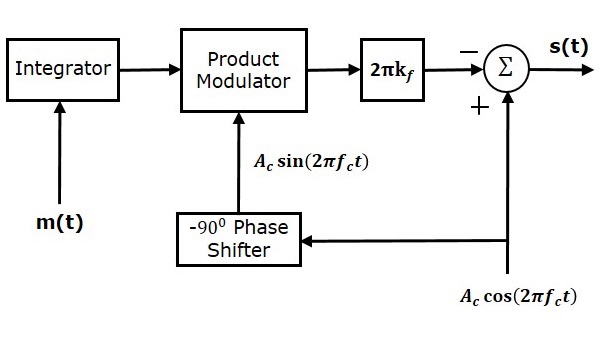
Ниже приведена блок-схема квадратичного модулятора

Пусть модулирующие и несущие сигналы обозначаются как $m \ left (t \ right)$ и $A \ cos \ left (2 \ pi f_ct \ right)$ соответственно. Эти два сигнала применяются в качестве входных данных для блока летнего (сумматора). Этот летний блок выдает выходной сигнал, который является сложением модулирующего и несущего сигналов. Математически мы можем записать это как

$$V_1t = m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right)$$

Этот сигнал $V_1t$ подается на вход нелинейного устройства, такого как диод. Характеристики диода тесно связаны с квадратичным законом.

$V_2t = k_1V_1 \ left (t \ right) + k_2V_1 ^ 2 \ left (t \ right)$ (уравнение 1)

Где $k_1$ и $k_2$ — постоянные.

Замените $V_1 \ left (t \ right)$ в уравнении 1

$$V_2 \ left (t \ right) = k_1 \ left [m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) \ right] + k_2 \ left [m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) \ right] ^ 2$$

$\ Rightarrow V_2 \ left (t \ right) = k_1 m \ left (t \ right) + k_1 A_c \ cos \ left (2 \ pi f_ct \ right) + k_2 m ^ 2 \ left (t \ right) +$

$k_2A_c ^ 2 \ cos ^ 2 \ left (2 \ pi f_ct \ right) + 2k_2m \ left (t \ right) A_c \ cos \ left (2 \ pi f_ct \ right)$

$\ Rightarrow V_2 \ left (t \ right) = k_1 m \ left (t \ right) + k_2 m ^ 2 \ left (t \ right) + k_2 A ^ 2_c \ cos ^ 2 \ left (2 \ pi f_ct \ справа) +$

$k_1A_c \ left [1+ \ left (\ frac {2k_2} {k_1} \ right) m \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$

Последний член вышеприведенного уравнения представляет желаемую волну AM, а первые три члена вышеприведенного уравнения являются нежелательными. Итак, с помощью полосового фильтра мы можем пропустить только АМ волну и исключить первые три члена.

Следовательно, на выходе квадратичного модулятора

$$s \ left (t \ right) = k_1A_c \ left [1+ \ left (\ frac {2k_2} {k_1} \ right) m \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$$

Стандартное уравнение AM-волны

$$s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$$

Где $K_a$ — амплитудная чувствительность

Сравнивая выходные данные квадратичного модулятора со стандартным уравнением AM-волны, мы получим коэффициент масштабирования как $k_1$ и амплитудную чувствительность $k_a$ как $\ frac {2k_2} {k1}$.

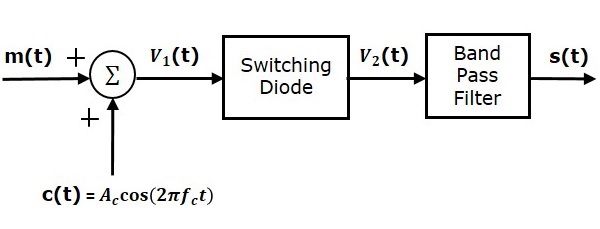
Модулятор переключения

Ниже приведена блок-схема переключения модулятора.

Переключающий модулятор похож на квадратичный модулятор. Единственное отличие состоит в том, что в квадратичном модуляторе диод работает в нелинейном режиме, тогда как в переключающем модуляторе диод должен работать как идеальный переключатель.

Пусть модулирующие и несущие сигналы обозначаются как $m \ left (t \ right)$ и $c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right)$ соответственно. Эти два сигнала применяются в качестве входных данных для блока летнего (сумматора). Летний блок выдает выходной сигнал, который является сложением модулирующих и несущих сигналов. Математически мы можем записать это как

$$V_1 \ left (t \ right) = m \ left (t \ right) + c \ left (t \ right) = m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) )$$

Этот сигнал $V_1 \ left (t \ right)$ применяется как вход диода. Предположим, что величина модулирующего сигнала очень мала по сравнению с амплитудой несущего сигнала $A_c$. Таким образом, действие включения и выключения диода контролируется сигналом несущей $c \ left (t \ right)$. Это означает, что диод будет смещен в прямом направлении, когда $c \ left (t \ right)> 0$, и будет смещен в обратном направлении, когда $c \ left (t \ right) <0$.

Следовательно, выход диода

$$V_2 \ left (t \ right) = \ left \ {\ begin {matrix} V_1 \ left (t \ right) & if & c \ left (t \ right)> 0 \\ 0 & if & c \ left (t \ right) <0 \ end {matrix} \ right.$$

Мы можем приблизить это как

$V_2 \ left (t \ right) = V_1 \ left (t \ right) x \ left (t \ right)$ (уравнение 2)

Где $x \ left (t \ right)$ — периодическая последовательность импульсов с периодом времени $T = \ frac {1} {f_c}$

Представление этой периодической последовательности импульсов в рядах Фурье

$$x \ left (t \ right) = \ frac {1} {2} + \ frac {2} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ справа) ^ n-1} {2n-1} \ cos \ left (2 \ pi \ left (2n-1 \ right) f_ct \ right)$$

$$\ Rightarrow x \ left (t \ right) = \ frac {1} {2} + \ frac {2} {\ pi} \ cos \ left (2 \ pi f_ct \ right) - \ frac {2} { 3 \ pi} \ cos \ left (6 \ pi f_ct \ right) + ....$$

Подставьте значения $V_1 \ left (t \ right)$ и $x \ left (t \ right)$ в уравнение 2.

$V_2 \ left (t \ right) = \ left [m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) \ right] \ left [\ frac {1} {2} + \ frac {2} {\ pi} \ cos \ left (2 \ pi f_ct \ right) - \ frac {2} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) + ..... \ right]$

$V_2 \ left (t \ right) = \ frac {m \ left (t \ right)} {2} + \ frac {A_c} {2} \ cos \ left (2 \ pi f_ct \ right) + \ frac { 2m \ left (t \ right)} {\ pi} \ cos \ left (2 \ pi f_ct \ right) + \ frac {2A_c} {\ pi} \ cos ^ 2 \ left (2 \ pi f_ct \ right) -$

$\ frac {2m \ left (t \ right)} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) - \ frac {2A_c} {3 \ pi} \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (6 \ pi f_ct \ right) + .....$

$V_2 \ left (t \ right) = \ frac {A_c} {2} \ left (1+ \ left (\ frac {4} {\ pi A_c} \ right) m \ left (t \ right) \ right) \ cos \ left (2 \ pi f_ct \ right) + \ frac {m \ left (t \ right)} {2} + \ frac {2A_c} {\ pi} \ cos ^ 2 \ left (2 \ pi f_ct \ правильно) -$

$\ frac {2m \ left (t \ right)} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) - \ frac {2A_c} {3 \ pi} \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (6 \ pi f_ct \ right) + .....$

1- ^й член приведенного выше уравнения представляет желаемую AM-волну, а остальные члены являются нежелательными. Таким образом, с помощью полосового фильтра мы можем пропустить только АМ волну и исключить оставшиеся члены.

Следовательно, выход модулятора переключения

$$s \ left (t \ right) = \ frac {A_c} {2} \ left (1+ \ left (\ frac {4} {\ pi A_c} \ right) m \ left (t \ right) \ right ) \ cos \ left (2 \ pi f_ct \ right)$$

Мы знаем, что стандартное уравнение AM волны

$$s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$$

Где $k_a$ — амплитудная чувствительность.

Сравнивая выходной сигнал переключающего модулятора со стандартным уравнением АМ волны, мы получим масштабный коэффициент как 0,5 и амплитудную чувствительность $k_a$ как $\ frac {4} {\ pi A_c}$.

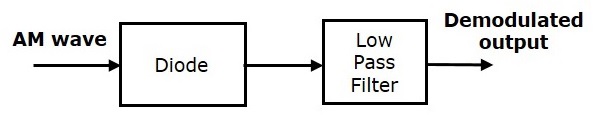
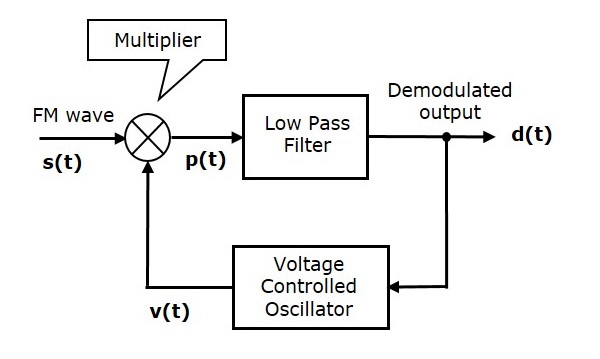
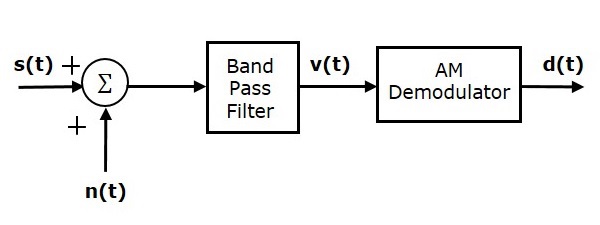
Аналоговая связь — AM демодуляторы

Процесс извлечения исходного сигнала сообщения из модулированной волны известен как обнаружение или демодуляция . Схема, которая демодулирует модулированную волну, называется демодулятором . Следующие демодуляторы (детекторы) используются для демодуляции AM-волны.

• Квадратный Закон Демодулятор
• Детектор конвертов

Квадратный Закон Демодулятор

Квадратный демодулятор используется для демодуляции АМ-волны низкого уровня. Ниже приведена блок-схема квадратичного демодулятора .

Этот демодулятор содержит устройство квадратичного типа и фильтр нижних частот. Волна АМ $V_1 \ left (t \ right)$ применяется в качестве входа для этого демодулятора.

Стандартная форма волны AM

$$V_1 \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$$

Мы знаем, что математическое соотношение между входом и выходом устройства квадратичного закона

$V_2 \ left (t \ right) = k_1V_1 \ left (t \ right) + k_2V_1 ^ 2 \ left (t \ right)$ (уравнение 1)

Куда,

$V_1 \ left (t \ right)$ — вход устройства квадратичного закона, который является ничем иным, как волной AM

$V_2 \ left (t \ right)$ — выход устройства квадратичного закона

$k_1$ и $k_2$ являются константами

Замените $V_1 \ left (t \ right)$ в уравнении 1

$$V_2 \ left (t \ right) = k_1 \ left (A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) \ right) + k_2 \ left (A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) \ right) ^ 2$$

$\ Rightarrow V_2 \ left (t \ right) = k_1A_c \ cos \ left (2 \ pi f_ct \ right) + k_1A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) +$

$k_2 {A_ {c}} ^ {2} \ left [1+ {K_ {a}} ^ {2} m ^ 2 \ left (t \ right) + 2k_am \ left (t \ right) \ right] \ left (\ frac {1+ \ cos \ left (4 \ pi f_ct \ right)} {2} \ right)$

$\ Rightarrow V_2 \ left (t \ right) = k_1A_c \ cos \ left (2 \ pi f_ct \ right) + k_1A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + \ frac { K_2 {A_ {с}} ^ {2}} {2} +$

$\ frac {K_2 {A_ {c}} ^ {2}} {2} \ cos \ left (4 \ pi f_ct \ right) + \ frac {k_2 {A_ {c}} ^ {2} {k_ {a }} ^ {2} m ^ 2 \ left (t \ right)} {2} + \ frac {k_2 {A_ {c}} ^ {2} {k_ {a}} ^ {2} m ^ 2 \ left (t \ right)} {2} \ cos \ left (4 \ pi f_ct \ right) +$

$k_2 {A_ {c}} ^ {2} k_am \ left (t \ right) + k_2 {A_ {c}} ^ {2} k_am \ left (t \ right) \ cos \ left (4 \ pi f_ct \ верно)$

В приведенном выше уравнении термин $k_2 {A_ {c}} ^ {2} k_am \ left (t \ right)$ является масштабированной версией сигнала сообщения. Его можно извлечь, пропустив вышеуказанный сигнал через фильтр нижних частот, а компонент постоянного тока $\ frac {k_2 {A_ {c}} ^ {2}} {2}$ можно устранить с помощью конденсатора связи.

Детектор конвертов

Детектор огибающей используется для обнаружения (демодуляции) AM-волны высокого уровня. Ниже приведена блок-схема детектора огибающей.

Этот детектор огибающей состоит из диода и фильтра низких частот. Здесь диод является основным детектирующим элементом. Следовательно, детектор огибающей также называется диодным детектором . Фильтр нижних частот содержит параллельную комбинацию резистора и конденсатора.

Волна АМ $s \ left (t \ right)$ применяется в качестве входных данных для этого детектора.

Мы знаем, что стандартная форма волны AM

$$s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$$

В положительном полупериоде AM-волны диод проводит, и конденсатор заряжается до пикового значения AM-волны. Когда значение волны AM меньше, чем это значение, диод будет иметь обратное смещение. Таким образом, конденсатор будет разряжаться через резистор R до следующего положительного полупериода AM-волны. Когда значение волны AM больше, чем напряжение на конденсаторе, диод проводит, и процесс будет повторяться.

Мы должны выбирать значения компонентов таким образом, чтобы конденсатор заряжался очень быстро и разряжался очень медленно. В результате мы получим форму волны напряжения на конденсаторе, аналогичную огибающей волны AM, которая почти аналогична модулирующему сигналу.

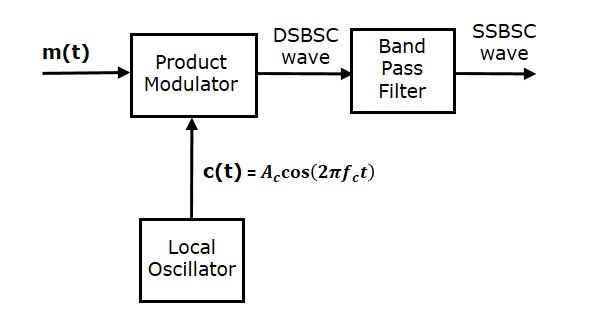
Аналоговая связь — DSBSC Модуляция

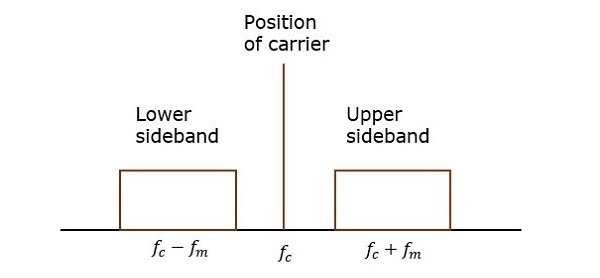
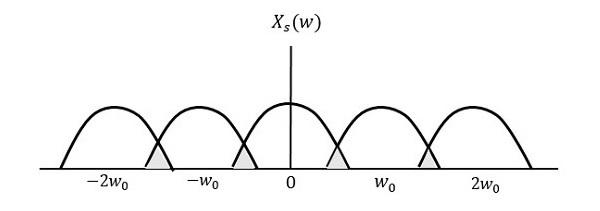
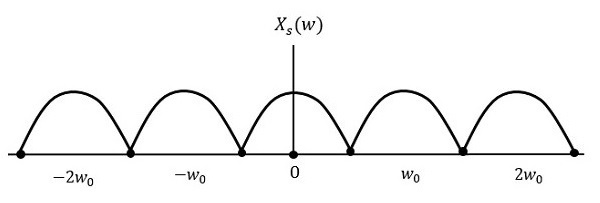
В процессе амплитудной модуляции модулированная волна состоит из несущей и двух боковых полос. Модулированная волна имеет информацию только в боковых полосах. Боковая полоса — это не что иное, как полоса частот, содержащая мощность, которые являются более низкими и более высокими частотами несущей частоты.

Передача сигнала, который содержит несущую вместе с двумя боковыми полосами, может называться двухполосной системой с полной несущей или просто DSBFC . Он построен, как показано на следующем рисунке.

Однако такая передача неэффективна. Потому что две трети энергии тратится впустую на несущей, которая не несет никакой информации.

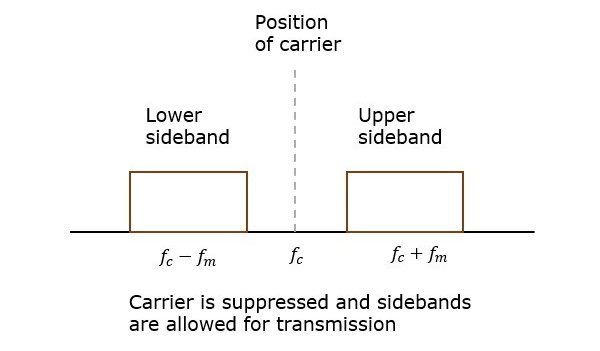
Если эта несущая подавляется и сохраненная мощность распределяется по двум боковым полосам , то такой процесс называется системой с двухполосной подавленной несущей или просто DSBSC . Он построен, как показано на следующем рисунке.

Математические выражения

Рассмотрим те же математические выражения для модулирующих сигналов и сигналов несущей, которые мы рассматривали в предыдущих главах.

т.е. модулирующий сигнал

$$m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right)$$

Сигнал несущей

$$c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right)$$

Математически мы можем представить уравнение волны DSBSC как произведение модулирующих и несущих сигналов.

$$s \ left (t \ right) = m \ left (t \ right) c \ left (t \ right)$$

$$\ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt \ right) \ cos \ left (2 \ pi f_ct \ right)$$

Пропускная способность DSBSC Wave

Мы знаем, что формула для пропускной способности (BW)

$$BW = F_ {макс} -f_ {мин}$$

Рассмотрим уравнение DSBSC модулированной волны.

$$s \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt \ right) \ cos (2 \ pi f_ct)$$

$$\ Rightarrow s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ frac {A_mA_c} {2 } \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right]$$

Волна с модуляцией DSBSC имеет только две частоты. Таким образом, максимальная и минимальная частоты составляют $f_c + f_m$ и $f_c-f_m$ соответственно.

т.е.

$f_ {max} = f_c + f_m$ и $f_ {min} = f_c-f_m$

Подставьте значения $f_ {max}$ и $f_ {min}$ в формулу пропускной способности.

$$BW = f_c + f_m- \ left (f_c-f_m \ right)$$

$$\ Rightarrow BW = 2f_m$$

Таким образом, ширина полосы волны DSBSC такая же, как у волны AM, и она равна удвоенной частоте модулирующего сигнала.

Расчеты мощности DSBSC Wave

Рассмотрим следующее уравнение DSBSC модулированной волны.

$$s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right]$$

Мощность волны DSBSC равна сумме мощностей частотной составляющей верхней боковой полосы и нижней боковой полосы.

$$p_t = Р- {USB} + Р- {LSB}$$

Мы знаем, что стандартная формула для мощности сигнала cos

$$P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m \ sqrt {2} \ right) ^ 2} {R}$$

Во-первых, давайте найдем мощности верхней боковой полосы и нижней боковой полосы одну за другой.

Мощность верхней боковой полосы

$$P_ {USB} = \ frac {\ left (A_mA_c / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R}$$

Точно так же мы получим мощность нижней боковой полосы, равную мощности верхней боковой полосы.

$$Р- {USB} = \ гидроразрыва {{A_ {т}} ^ {2} {A_ {с}} ^ {2}} {8R}$$

Теперь давайте добавим эти две мощности боковой полосы, чтобы получить мощность волны DSBSC.

$$p_t = \ гидроразрыва {{А_ {т}} ^ {2} {А_ {C}} ^ {2}} {8R} + \ гидроразрыва {{А_ {т}} ^ {2} {А_ {C} } ^ {2}} {8R}$$

$$\ Rightarrow P_t = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {4R}$$

Следовательно, мощность, необходимая для передачи волны DSBSC, равна мощности обеих боковых полос.

Аналоговая связь — DSBSC Модуляторы

В этой главе давайте поговорим о модуляторах, которые генерируют волну DSBSC. Следующие два модулятора генерируют волну DSBSC.

• Сбалансированный модулятор
• Кольцевой модулятор

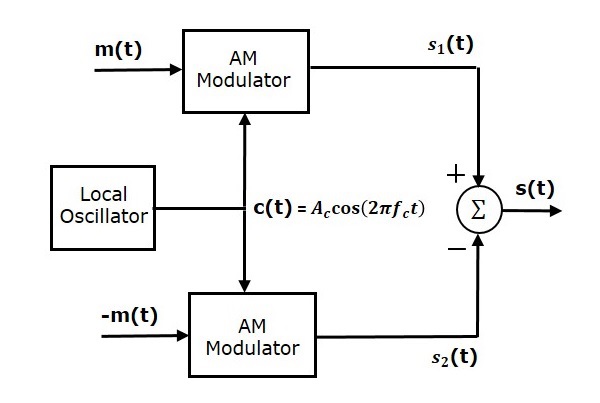
Сбалансированный Модулятор

Ниже приведена блок-схема сбалансированного модулятора.

Сбалансированный модулятор состоит из двух идентичных AM-модуляторов. Эти два модулятора расположены в сбалансированной конфигурации, чтобы подавить сигнал несущей. Следовательно, он называется сбалансированным модулятором.

Тот же самый сигнал несущей $c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right)$ применяется в качестве одного из входов для этих двух модуляторов AM. Модулирующий сигнал $m \ left (t \ right)$ подается в качестве другого входа в верхний AM-модулятор. Принимая во внимание, что модулирующий сигнал $m \ left (t \ right)$ с противоположной полярностью, то есть $-m \ left (t \ right)$, применяется в качестве другого входа в нижний AM-модулятор.

Выход верхнего AM модулятора

$$s_1 \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$$

Выход нижнего AM модулятора

$$s_2 \ left (t \ right) = A_c \ left [1-k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$$

Мы получаем DSBSC волну $s \ left (t \ right)$, вычитая $s_2 \ left (t \ right)$ из $s_1 \ left (t \ right)$. Летний блок используется для выполнения этой операции. $s_1 \ left (t \ right)$ с положительным знаком и $s_2 \ left (t \ right)$ с отрицательным знаком применяются в качестве входных данных для летнего блока. Таким образом, летний блок производит вывод $s \ left (t \ right)$, который является разностью $s_1 \ left (t \ right)$ и $s_2 \ left (t \ right)$.

$$\ Rightarrow s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) -A_c \ left [1-k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$$

$$\ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) - A_c \ cos \ left (2 \ pi f_ct \ right) +$$

$A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right)$

$\ Rightarrow s \ left (t \ right) = 2A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right)$

Мы знаем, что стандартное уравнение DSBSC волны

$$s \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right)$$

Сравнивая выходные данные летнего блока со стандартным уравнением волны DSBSC, мы получим коэффициент масштабирования как $2k_a$

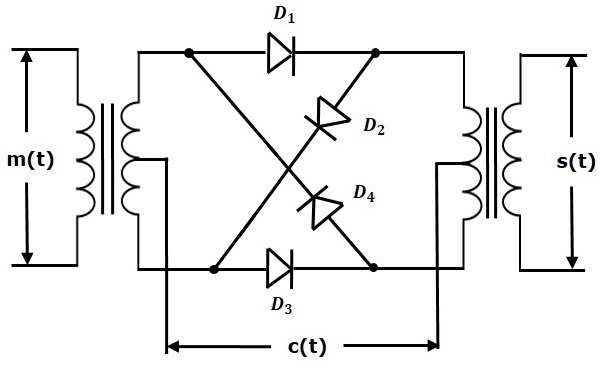
Кольцевой Модулятор

Ниже приведена блок-схема кольцевого модулятора.

На этой диаграмме четыре диода $D_1$, $D_2$, $D_3$ и $D_4$ соединены в кольцевую структуру. Следовательно, этот модулятор называется кольцевым модулятором . На этой диаграмме используются два трансформатора с центральным отводом. Сигнал сообщения $m \ left (t \ right)$ подается на входной преобразователь. Принимая во внимание, что несущие сигналы $c \ left (t \ right)$ подаются между двумя трансформаторами с центральным ответвлением.

Для положительного полупериода несущего сигнала диоды $D_1$ и $D_3$ включены, а два других диода $D_2$ и $D_4$ выключены. В этом случае сигнал сообщения умножается на +1.

Для отрицательного полупериода сигнала несущей диоды $D_2$ и $D_4$ включены, а два других диода $D_1$ и $D_3$ выключены. В этом случае сигнал сообщения умножается на -1. Это приводит к сдвигу фазы $ 180 ^ 0 в результирующей волне DSBSC.

Из приведенного выше анализа можно сказать, что четыре диода $D_1$, $D_2$, $D_3$ и $D_4$ управляются сигналом несущей. Если носитель представляет собой прямоугольную волну, то представление ряда Фурье в $c \ left (t \ right)$ представляется в виде

$$c \ left (t \ right) = \ frac {4} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ right) ^ {n-1}} {2n-1} \ cos \ left [2 \ pi f_ct \ left (2n-1 \ right) \ right]$$

Мы получим волну DSBSC $s \ left (t \ right)$, которая является просто произведением сигнала-носителя $c \ left (t \ right)$ и сигнала сообщения $m \ left (t \ right)$ ie ,

$$s \ left (t \ right) = \ frac {4} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ right) ^ {n-1}} {2n-1} \ cos \ left [2 \ pi f_ct \ left (2n-1 \ right) \ right] m \ left (t \ right)$$

Приведенное выше уравнение представляет волну DSBSC, которая получается на выходе трансформатора кольцевого модулятора.

Модуляторы DSBSC также называют модуляторами продукта, поскольку они производят выходной сигнал, который является произведением двух входных сигналов.

DSBSC Демодуляторы

Процесс извлечения исходного сигнала сообщения из волны DSBSC известен как обнаружение или демодуляция DSBSC. Следующие демодуляторы (детекторы) используются для демодуляции волны DSBSC.

• Когерентный детектор
• Костас Луп

Когерентный детектор

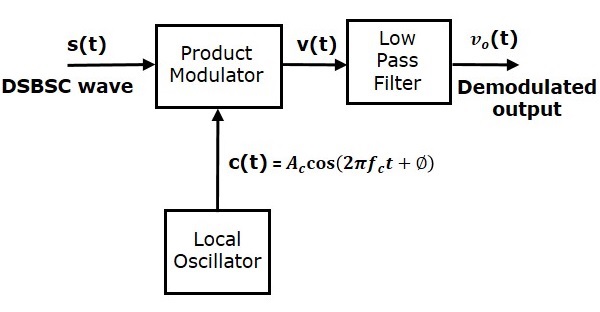
Здесь один и тот же сигнал несущей (который используется для генерации сигнала DSBSC) используется для обнаружения сигнала сообщения. Следовательно, этот процесс обнаружения называется когерентным или синхронным обнаружением . Ниже приведена блок-схема когерентного детектора.

В этом процессе сигнал сообщения может быть извлечен из волны DSBSC путем умножения его на несущую, имеющую ту же частоту и фазу несущей, которые используются в модуляции DSBSC. Полученный сигнал затем пропускается через фильтр нижних частот. Выход этого фильтра — желаемый сигнал сообщения.

Пусть волна DSBSC будет

$$s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right)$$

Выход гетеродина

$$c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ phi \ right)$$

Где $\ phi$ — разность фаз между сигналом гетеродина и сигналом несущей, который используется для модуляции DSBSC.

Из рисунка мы можем записать вывод модулятора продукта как

$$v \ left (t \ right) = s \ left (t \ right) c \ left (t \ right)$$

Подставим значения $s \ left (t \ right)$ и $c \ left (t \ right)$ в вышеприведенном уравнении.

$$\ Rightarrow v \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) A_c \ cos \ left (2 \ pi f_ct + \ phi \ right)$$

$= {A_ {c}} ^ {2} \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct + \ phi \ right) m \ left (t \ right)$

$= \ frac {{A_ {c}} ^ {2}} {2} \ left [\ cos \ left (4 \ pi f_ct + \ phi \ right) + \ cos \ phi \ right] m \ left (t \ верно)$

$$v \ left (t \ right) = \ frac {{A_ {c}} ^ {2}} {2} \ cos \ phi m \ left (t \ right) + \ frac {{A_ {c}} ^ {2}} {2} \ cos \ left (4 \ pi f_ct + \ phi \ right) m \ left (t \ right)$$

В приведенном выше уравнении первый член — это масштабированная версия сигнала сообщения. Его можно извлечь, пропустив вышеуказанный сигнал через фильтр нижних частот.

Следовательно, выходной сигнал фильтра нижних частот

$$v_0t = \ frac {{A_ {c}} ^ {2}} {2} \ cos \ phi m \ left (t \ right)$$

Амплитуда демодулированного сигнала будет максимальной, когда $\ phi = 0 ^ 0$. Вот почему сигнал гетеродина и сигнал несущей должны быть в фазе, т.е. между этими двумя сигналами не должно быть разности фаз.

Амплитуда демодулированного сигнала будет равна нулю, когда $\ phi = \ pm 90 ^ 0$. Этот эффект называется квадратурным нулевым эффектом .

Костас Луп

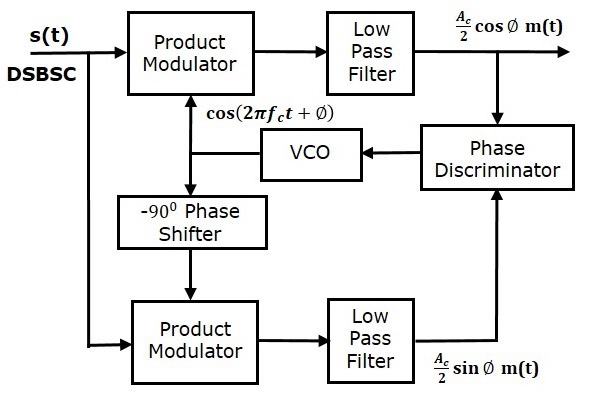
Петля Костаса используется, чтобы сделать как сигнал несущей (используемый для модуляции DSBSC), так и локально сгенерированный сигнал в фазе. Ниже приведена блок-схема цикла Костаса.

Цикл Костаса состоит из двух модуляторов произведений с общим входом $s \ left (t \ right)$, который является волной DSBSC. Другой вход для обоих модуляторов продукта берется из генератора с управляемым напряжением (VCO) с фазовым сдвигом $-90 ^ 0$ к одному из модуляторов продукта, как показано на рисунке.

Мы знаем, что уравнение DSBSC волны

$$s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right)$$

Пусть выход VCO будет

$$c_1 \ left (t \ right) = \ cos \ left (2 \ pi f_ct + \ phi \ right)$$

Этот выход VCO применяется как вход несущей модулятора верхнего продукта.

Следовательно, выход верхнего модулятора произведения

$$v_1 \ left (t \ right) = s \ left (t \ right) c_1 \ left (t \ right)$$

Подставьте значения $s \ left (t \ right)$ и $c_1 \ left (t \ right)$ в вышеприведенном уравнении.

$$ \ Rightarrow v_1 \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) \ cos \ left (2 \ pi f_ct + \ phi \ right) $ $

После упрощения мы получим $v_1 \ left (t \ right)$ как

$$v_1 \ left (t \ right) = \ frac {A_c} {2} \ cos \ phi m \ left (t \ right) + \ frac {A_c} {2} \ cos \ left (4 \ pi f_ct + \ phi \ right) m \ left (t \ right)$$

Этот сигнал применяется как вход верхнего фильтра нижних частот. Выход этого фильтра нижних частот

$$v_ {01} \ left (t \ right) = \ frac {A_c} {2} \ cos \ phi m \ left (t \ right)$$

Следовательно, выходной сигнал этого фильтра нижних частот является масштабированной версией модулирующего сигнала.

Выход $-90 ^ 0$ сдвигателя фазы

$$c_2 \ left (t \ right) = cos \ left (2 \ pi f_ct + \ phi-90 ^ 0 \ right) = \ sin \ left (2 \ pi f_ct + \ phi \ right)$$

Этот сигнал применяется как вход несущей модулятора нижнего произведения.

Выход нижнего продукта модулятора

$$v_2 \ left (t \ right) = s \ left (t \ right) c_2 \ left (t \ right)$$

Подставьте значения $s \ left (t \ right)$ и $c_2 \ left (t \ right)$ в вышеприведенном уравнении.

$$ \ Rightarrow v_2 \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) \ sin \ left (2 \ pi f_ct + \ phi \ right) $ $

После упрощения мы получим $v_2 \ left (t \ right)$ как

$$v_2 \ left (t \ right) = \ frac {A_c} {2} \ sin \ phi m \ left (t \ right) + \ frac {A_c} {2} \ sin \ left (4 \ pi f_ct + \ ph \ right) m \ left (t \ right)$$

Этот сигнал применяется как вход нижнего фильтра нижних частот. Выход этого фильтра нижних частот

$$v_ {02} \ left (t \ right) = \ frac {A_c} {2} \ sin \ phi m \ left (t \ right)$$

Выход этого низкочастотного фильтра имеет разность фаз $-90 ^ 0$ с выходом верхнего фильтра нижних частот.

Выходы этих двух фильтров нижних частот применяются в качестве входов фазового дискриминатора. На основе разности фаз между этими двумя сигналами дискриминатор фазы вырабатывает управляющий сигнал постоянного тока.

Этот сигнал применяется в качестве входа VCO для исправления фазовой ошибки на выходе VCO. Следовательно, сигнал несущей (используемый для модуляции DSBSC) и локально сгенерированный сигнал (выход VCO) находятся в фазе.

Аналоговая связь — SSBSC Модуляция

В предыдущих главах мы обсуждали модуляцию и демодуляцию DSBSC. DSBSC модулированный сигнал имеет две боковые полосы. Поскольку две боковые полосы несут одинаковую информацию, нет необходимости передавать обе боковые полосы. Мы можем устранить одну боковую полосу.

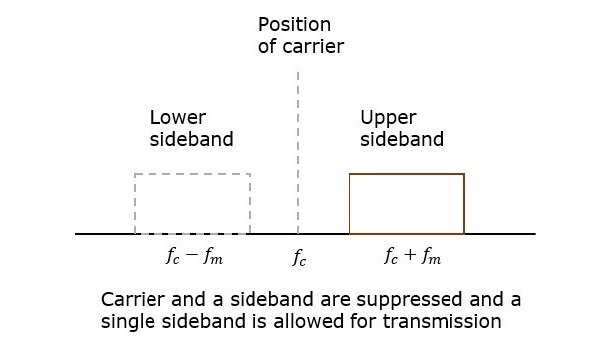
Процесс подавления одной из боковых полос вместе с несущей и передачи одной боковой полосы называется системой с подавленной несущей с одной боковой полосой или просто SSBSC . Он построен, как показано на следующем рисунке.

На приведенном выше рисунке несущая и нижняя боковая полоса подавлены. Следовательно, верхняя боковая полоса используется для передачи. Точно так же мы можем подавить несущую и верхнюю боковую полосу при передаче нижней боковой полосы.

Эта система SSBSC, которая передает одну боковую полосу, имеет высокую мощность, поскольку мощность, выделенная как для несущей, так и для другой боковой полосы, используется при передаче этой одной боковой полосы.

Математические выражения

Рассмотрим те же математические выражения для модулирующего и несущего сигналов, которые мы рассматривали в предыдущих главах.

т.е. модулирующий сигнал

$$m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right)$$

Сигнал несущей

$$c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right)$$

Математически мы можем представить уравнение волны SSBSC как

$s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right]$ для верхней боковой полосы

Или же

$s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right]$ для нижней боковой полосы

Пропускная способность SSBSC Wave

Мы знаем, что модулированная волна DSBSC содержит две боковые полосы и ее полоса пропускания составляет $2f_m$. Поскольку модулированная волна SSBSC содержит только одну боковую полосу, ее ширина составляет половину ширины полосы модулированной волны DSBSC.

т. е. полоса пропускания модулированной волны SSBSC = $\ frac {2f_m} {2} = f_m$

Следовательно, ширина полосы модулированной волны SSBSC составляет $f_m$, и она равна частоте модулирующего сигнала.

Расчеты мощности SSBSC Wave

Рассмотрим следующее уравнение SSBSC модулированной волны.

$s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right]$ для верхней боковой полосы

Или же

$s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right]$ для нижней боковой полосы

Мощность волны SSBSC равна мощности любых частотных составляющих одной боковой полосы.

$$p_t = Р- {USB} = Р- {LSB}$$

Мы знаем, что стандартная формула для мощности сигнала cos

$$P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m / \ sqrt {2} \ right) ^ 2} {R}$$

В этом случае мощность верхней боковой полосы равна

$$P_ {USB} = \ frac {\ left (A_m A_c / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {m}} ^ {2} {A_ {c} } ^ {2}} {8R}$$

Точно так же мы получим мощность нижней боковой полосы такую ​​же, как и мощность верхней боковой полосы.

$$P_ {LSB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R}$$

Следовательно, мощность волны SSBSC равна

$$P_t = P_ {USB} = P_ {LSB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R}$$

преимущества

• Ширина полосы или занимаемого спектрального пространства меньше, чем у волн AM и DSBSC.

• Допускается передача большего количества сигналов.

• Власть сохранена.

• Сигнал высокой мощности может быть передан.

• Меньшее количество шума присутствует.

• Затухание сигнала менее вероятно.

Ширина полосы или занимаемого спектрального пространства меньше, чем у волн AM и DSBSC.

Допускается передача большего количества сигналов.

Власть сохранена.

Сигнал высокой мощности может быть передан.

Меньшее количество шума присутствует.

Затухание сигнала менее вероятно.

Недостатки

• Генерация и обнаружение волны SSBSC является сложным процессом.

• Качество сигнала ухудшается, если передатчик и приемник SSB не имеют превосходной стабильности частоты.

Генерация и обнаружение волны SSBSC является сложным процессом.

Качество сигнала ухудшается, если передатчик и приемник SSB не имеют превосходной стабильности частоты.

Приложения

• Для требований энергосбережения и низкой пропускной способности.

• В наземной, воздушной и морской мобильной связи.

• В двухточечной связи.

• В радиосвязи.

• В телевидении, телеметрии и радиолокации.

• В военных сообщениях, таких как любительское радио и т. Д.

Для требований энергосбережения и низкой пропускной способности.

В наземной, воздушной и морской мобильной связи.

В двухточечной связи.

В радиосвязи.

В телевидении, телеметрии и радиолокации.

В военных сообщениях, таких как любительское радио и т. Д.

Аналоговая связь — модуляторы SSBSC

В этой главе давайте поговорим о модуляторах, которые генерируют волну SSBSC. Мы можем генерировать волну SSBSC, используя следующие два метода.

• Метод частотной дискриминации
• Метод фазовой дискриминации

Метод частотной дискриминации

На следующем рисунке показана блок-схема модулятора SSBSC с использованием метода частотной дискриминации.

В этом методе сначала мы сгенерируем волну DSBSC с помощью модулятора продукта. Затем примените эту волну DSBSC в качестве входа полосового фильтра. Этот полосовой фильтр производит выходной сигнал, который является волной SSBSC.

Выберите диапазон частот полосового фильтра в качестве спектра желаемой волны SSBSC. Это означает, что полосовой фильтр можно настроить на частоты либо верхней, либо нижней боковой полосы, чтобы получить соответствующую волну SSBSC, имеющую верхнюю или нижнюю боковую полосу.

Метод фазовой дискриминации

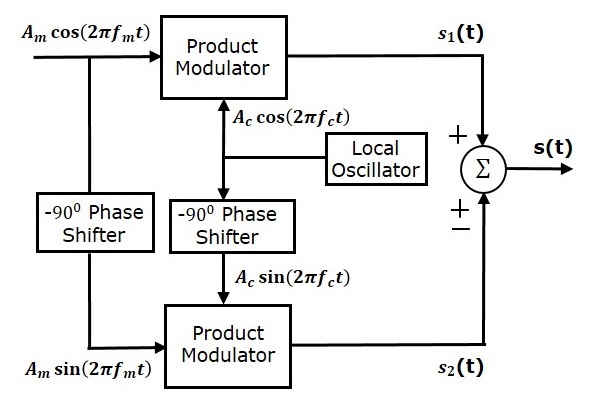
На следующем рисунке показана блок-схема модулятора SSBSC с использованием метода фазовой дискриминации.

Эта блок-схема состоит из двух модуляторов произведений, двух $-90 ^ 0$ фазовращателей, одного локального генератора и одного летнего блока. Модулятор продукта производит выход, который является произведением двух входов. Фазовращатель $-90 ^ 0$ создает выходной сигнал, который имеет фазовую задержку $-90 ^ 0$ относительно входа.

Локальный генератор используется для генерации сигнала несущей. Летний блок создает выходной сигнал, который представляет собой либо сумму двух входов, либо разницу двух входов в зависимости от полярности входов.

Модулирующий сигнал $A_m \ cos \ left (2 \ pi f_mt \ right)$ и несущий сигнал $A_c \ cos \ left (2 \ pi f_ct \ right)$ непосредственно применяются в качестве входных данных для модулятора верхнего произведения. Таким образом, верхний модулятор произведений производит результат, который является произведением этих двух входов.

Выход верхнего модулятора произведения

$$s_1 \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt \ right) \ cos \ left (2 \ pi f_ct \ right)$$

$$\ Rightarrow s_1 \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ right \}$$

Модулирующий сигнал $A_m \ cos \ left (2 \ pi f_mt \ right)$ и несущий сигнал $A_c \ cos \ left (2 \ pi f_ct \ right)$ сдвинуты по фазе на $-90 ^ 0$ перед применением в качестве входы в нижний продукт модулятора. Таким образом, модулятор нижнего произведения производит выход, который является произведением этих двух входов.

Выход нижнего продукта модулятора

$$s_2 \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt-90 ^ 0 \ right) \ cos \ left (2 \ pi f_ct-90 ^ 0 \ right)$$

$\ Rightarrow s_2 \ left (t \ right) = A_mA_c \ sin \ left (2 \ pi f_mt \ right) \ sin \ left (2 \ pi f_ct \ right)$

$\ Rightarrow s_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] - \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] \ right \}$

Добавьте $s_1 \ left (t \ right)$ и $s_2 \ left (t \ right)$, чтобы получить модулированную SSBSC волну $s \ left (t \ right)$, имеющую нижнюю боковую полосу.

$s \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ right \} +$

$\ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] - \ cos \ left [2 \ pi \ left (f_c + f_m \) справа) t \ right] \ right \}$

$\ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right]$

Вычтите $s_2 \ left (t \ right)$ из $s_1 \ left (t \ right)$, чтобы получить SSBSC-модулированную волну $s \ left (t \ right)$, имеющую верхнюю боковую полосу.

$s \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ right \} -$

$\ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] - \ cos \ left [2 \ pi \ left (f_c + f_m \) справа) t \ right] \ right \}$

$\ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right]$

Следовательно, при правильном выборе полярностей входов в летнем блоке мы получим волну SSBSC, имеющую верхнюю боковую полосу или нижнюю боковую полосу.

SSBSC Демодулятор

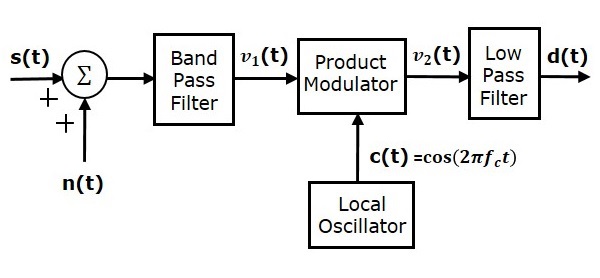
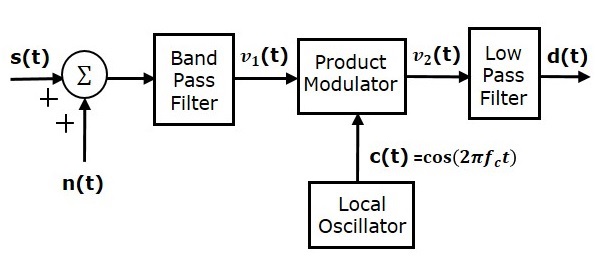
Процесс извлечения исходного сигнала сообщения из волны SSBSC известен как обнаружение или демодуляция SSBSC. Когерентный детектор используется для демодуляции волны SSBSC.

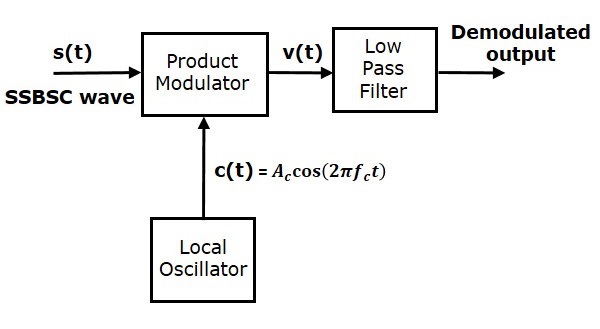
Когерентный детектор

Здесь тот же самый сигнал несущей (который используется для генерации волны SSBSC) используется для обнаружения сигнала сообщения. Следовательно, этот процесс обнаружения называется когерентным или синхронным обнаружением . Ниже приведена блок-схема когерентного детектора.

В этом процессе сигнал сообщения может быть извлечен из волны SSBSC путем умножения его на несущую, имеющую ту же частоту и фазу несущей, которые используются в модуляции SSBSC. Полученный сигнал затем пропускается через фильтр нижних частот. Выход этого фильтра — желаемый сигнал сообщения.

Рассмотрим следующую волну SSBSC, имеющую нижнюю боковую полосу .

$$s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right]$$

Выход гетеродина

$$c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right)$$

Из рисунка мы можем записать вывод модулятора продукта как

$$v \ left (t \ right) = s \ left (t \ right) c \ left (t \ right)$$

Подставьте значения $s \ left (t \ right)$ и $c \ left (t \ right)$ в вышеприведенном уравнении.

$$v \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] A_c \ cos \ left (2 \ pi f_ct \ право)$$

$= \ frac {A_m {A_ {c}} ^ {2}} {2} \ cos \ left [2 \ pi \ left (f_c -f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ право)$

$= \ frac {A_m {A_ {c}} ^ {2}} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c-fm \ right) \ right] + \ cos \ left ( 2 \ pi f_m \ right) t \ right \}$

$v \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) + \ frac {A_m {A_ {c} } ^ {2}} {4} \ cos \ left [2 \ pi \ left (2f_c-f_m \ right) t \ right]$

В приведенном выше уравнении первый член — это масштабированная версия сигнала сообщения. Его можно извлечь, пропустив вышеуказанный сигнал через фильтр нижних частот.

Следовательно, выходной сигнал фильтра нижних частот

$$v_0 \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right)$$

Здесь коэффициент масштабирования составляет $\ frac {{A_ {c}} ^ {2}} {4}$.

Мы можем использовать ту же блок-схему для демодуляции волны SSBSC, имеющей верхнюю боковую полосу. Рассмотрим следующую волну SSBSC, имеющую верхнюю боковую полосу .

$$s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right]$$

Выход гетеродина

$$c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right)$$

Мы можем записать вывод модулятора продукта как

$$v \ left (t \ right) = s \ left (t \ right) c \ left (t \ right)$$

Подставьте значения $s \ left (t \ right)$ и $c \ left (t \ right)$ в вышеприведенном уравнении.

$$\ Rightarrow v \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] A_c \ cos \ left (2 \ pi f_ct \ right)$$

$= \ frac {A_m {A_ {c}} ^ {2}} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ право)$

$= \ frac {A_m {A_ {c}} ^ {2}} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c + f_m \ right) t \ right] + \ cos \ left (2 \ pi f_mt \ right) \ right \}$

$v \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) + \ frac {A_m {A_ {c} } ^ {2}} {4} \ cos \ left [2 \ pi \ left (2f_c + f_m \ right) t \ right]$

В приведенном выше уравнении первый член — это масштабированная версия сигнала сообщения. Его можно извлечь, пропустив вышеуказанный сигнал через фильтр нижних частот.

Следовательно, выходной сигнал фильтра нижних частот

$$v_0 \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right)$$

Здесь также коэффициент масштабирования составляет $\ frac {{A_ {c}} ^ {2}} {4}$.

Следовательно, мы получаем одинаковый демодулированный выход в обоих случаях с помощью когерентного детектора.

Аналоговая связь — VSBSC Модуляция

В предыдущих главах мы обсуждали модуляцию и демодуляцию SSBSC. Модулированный сигнал SSBSC имеет только одну частоту боковой полосы. Теоретически, мы можем получить одну частотную составляющую боковой полосы полностью, используя идеальный полосовой фильтр. Однако практически мы не можем получить всю частотную составляющую боковой полосы. Из-за этого часть информации теряется.

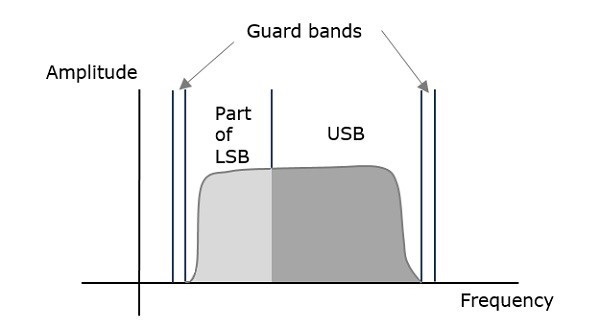
Чтобы избежать этой потери, выбирается метод, который является компромиссом между DSBSC и SSBSC. Этот метод известен как метод подавления несущей боковой полосы (VSBSC) . Слово «пережиток» означает «часть», из которой происходит название.

VSBSC Modulation — это процесс, при котором часть сигнала, называемая пережитком, модулируется вместе с одной боковой полосой. Частотный спектр волны VSBSC показан на следующем рисунке.

Наряду с верхней боковой полосой часть нижней боковой полосы также передается в этом методе. Точно так же мы можем передать нижнюю боковую полосу вместе с частью верхней боковой полосы. Защитная полоса очень малой ширины укладывается с обеих сторон VSB во избежание помех. VSB модуляция в основном используется в телевизионных передачах.

Пропускная способность модуляции VSBSC

Мы знаем, что полоса пропускания модулированной волны SSBSC составляет $f_m$. Поскольку модулированная волна VSBSC содержит частотные составляющие одной боковой полосы вместе с остатком другой боковой полосы, ее ширина полосы будет суммой ширины полосы частот модулированной волны SSBSC и частоты следа $f_v$.

т. е. полоса пропускания модулированной волны VSBSC = $f_m + f_v$

преимущества

Ниже приведены преимущества модуляции VSBSC.

• Очень эффективным.

• Уменьшение ширины полосы по сравнению с волнами AM и DSBSC.

• Конструкция фильтра проста, так как высокая точность не требуется.

• Передача низкочастотных компонентов возможна без каких-либо затруднений.

• Обладает хорошими фазовыми характеристиками.

Очень эффективным.

Уменьшение ширины полосы по сравнению с волнами AM и DSBSC.

Конструкция фильтра проста, так как высокая точность не требуется.

Передача низкочастотных компонентов возможна без каких-либо затруднений.

Обладает хорошими фазовыми характеристиками.

Недостатки

Ниже приведены недостатки VSBSC модуляции.

• Пропускная способность больше по сравнению с волной SSBSC.

• Демодуляция сложна.

Пропускная способность больше по сравнению с волной SSBSC.

Демодуляция сложна.

Приложения

Наиболее выдающееся и стандартное применение VSBSC — для передачи телевизионных сигналов. Кроме того, это наиболее удобный и эффективный метод, когда рассматривается использование полосы пропускания.

Теперь давайте обсудим модулятор, который генерирует волну VSBSC, и демодулятор, который демодулирует волну VSBSC один за другим.

Поколение VSBSC

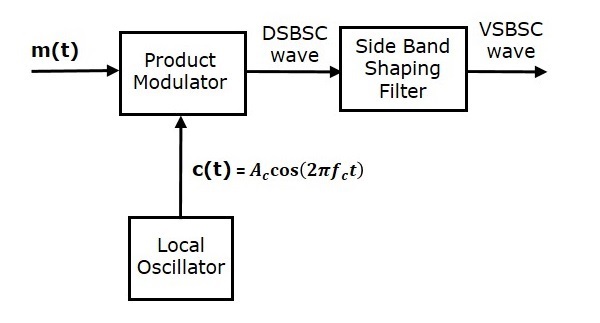
Генерация волны VSBSC аналогична генерации волны SSBSC. Модулятор VSBSC показан на следующем рисунке.

В этом методе сначала мы сгенерируем волну DSBSC с помощью модулятора продукта. Затем примените эту волну DSBSC в качестве входа фильтра формирования боковой полосы. Этот фильтр производит выходной сигнал, который является волной VSBSC.

Модулирующий сигнал $m \ left (t \ right)$ и несущий сигнал $A_c \ cos \ left (2 \ pi f_ct \ right)$ применяются в качестве входных данных для модулятора продукта. Следовательно, модулятор продукта производит выход, который является произведением этих двух входов.

Следовательно, выход модулятора продукта

$$p \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right)$$

Применить преобразование Фурье с обеих сторон

$$P \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right]$$

Вышеуказанное уравнение представляет собой уравнение частотного спектра DSBSC.

Пусть передаточная функция фильтра формирования боковых полос равна $H \ left (f \ right)$. Этот фильтр имеет вход $p \ left (t \ right)$, а на выходе — модулированная волна VSBSC $s \ left (t \ right)$. Преобразования Фурье для $p \ left (t \ right)$ и $s \ left (t \ right)$ равны $P \ left (t \ right)$ и $S \ left (t \ right)$ соответственно.

Математически мы можем записать $S \ left (f \ right)$ как

$$S \ left (t \ right) = P \ left (f \ right) H \ left (f \ right)$$

Замените значение $P \ left (f \ right)$ в приведенном выше уравнении.

$$S \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] H \ left ( f \ right)$$

Приведенное выше уравнение представляет собой уравнение частотного спектра VSBSC.

Демодуляция VSBSC

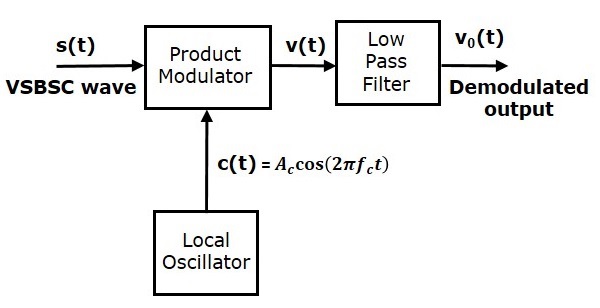
Демодуляция волны VSBSC аналогична демодуляции волны SSBSC. Здесь тот же сигнал несущей (который используется для генерации волны VSBSC) используется для обнаружения сигнала сообщения. Следовательно, этот процесс обнаружения называется когерентным или синхронным обнаружением . Демодулятор VSBSC показан на следующем рисунке.

В этом процессе сигнал сообщения может быть извлечен из волны VSBSC путем умножения его на несущую, которая имеет ту же частоту и фазу несущей, которые используются в модуляции VSBSC. Полученный сигнал затем пропускается через фильтр нижних частот. Выход этого фильтра — желаемый сигнал сообщения.

Пусть волна VSBSC будет $s \ left (t \ right)$, а сигнал несущей — $A_c \ cos \ left (2 \ pi f_ct \ right)$.

Из рисунка мы можем записать вывод модулятора продукта как

$$v \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) s \ left (t \ right)$$

Применить преобразование Фурье с обеих сторон

$$V \ left (f \ right) = \ frac {A_c} {2} \ left [S \ left (f-f_c \ right) + S \ left (f + f_c \ right) \ right]$$

Мы знаем, что $S \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] H \ влево (f \ right)$

Из приведенного выше уравнения найдем $S \ left (f-f_c \ right)$ и $S \ left (f + f_c \ right)$.

$$S \ left (f-f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c-f_c \ right) + M \ left (f-f_c + f_c \ right) \ вправо] H \ left (f-f_c \ right)$$

$\ Rightarrow S \ left (f-f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f-2f_c \ right) + M \ left (f \ right) \ right] H \ left (f-f_c \ right)$

$$S \ left (f + f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f + f_c-f_c \ right) + M \ left (f + f_c + f_c \ right) \ вправо] H \ left (f + f_c \ right)$$

$\ Rightarrow S \ left (f + f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f \ right) + M \ left (f + 2f_c \ right) \ right] H \ left (f + f_c \ right)$

Подставьте значения $S \ left (f-f_c \ right)$ и $S \ left (f + f_c \ right)$ в $V \ left (f \ right)$.

$V (f) = \ frac {A_c} {2} [\ frac {A_c} {2} [M (f-2f_c) + M (f)] H (f-f_c) +$

$\ Гидроразрыва {A_C} {2} [М (е) + М (F + 2f_c)] Н (F + F_C)]$

$\ Rightarrow V \ left (f \ right) = \ frac {{A_ {c}} ^ {2}} {4} M \ left (f \ right) \ left [H \ left (f-f_c \ right) + H \ left (f + f_c \ right) \ right]$

$+ \ frac {{A_ {c}} ^ {2}} {4} \ left [M \ left (f-2f_c \ right) H \ left (f-f_c \ right) + M \ left (f + 2f_c \ right) H \ left (f + f_c \ right) \ right]$

В приведенном выше уравнении первый член представляет масштабированную версию желаемого частотного спектра сигнала сообщения. Его можно извлечь, пропустив вышеуказанный сигнал через фильтр нижних частот.

$$V_0 \ left (f \ right) = \ frac {{A_ {c}} ^ {2}} {4} M \ left (f \ right) \ left [H \ left (f-f_c \ right) + H \ left (f + f_c \ right) \ right]$$

Аналоговая связь — угловая модуляция

Другим типом модуляции в непрерывно-волновой модуляции является угловая модуляция . Угловая модуляция — это процесс, в котором частота или фаза сигнала несущей изменяется в соответствии с сигналом сообщения.

Стандартное уравнение угловой модуляции волны

$$s \ left (t \ right) = A_c \ cos \ theta _i \ left (t \ right)$$

Куда,

$A_c$ — амплитуда модулированной волны, которая равна амплитуде несущего сигнала.

$\ theta _i \ left (t \ right)$ — угол модулированной волны

Угловая модуляция дополнительно делится на частотную модуляцию и фазовую модуляцию.

• Частотная модуляция — это процесс линейного изменения частоты сигнала несущей с сигналом сообщения.

• Фазовая модуляция — это процесс линейного изменения фазы сигнала несущей с сигналом сообщения.

Частотная модуляция — это процесс линейного изменения частоты сигнала несущей с сигналом сообщения.

Фазовая модуляция — это процесс линейного изменения фазы сигнала несущей с сигналом сообщения.

Теперь давайте обсудим это подробно.

Модуляция частоты

При амплитудной модуляции амплитуда несущего сигнала изменяется. Принимая во внимание, что в частотной модуляции (ЧМ) частота несущего сигнала изменяется в соответствии с мгновенной амплитудой модулирующего сигнала.

Следовательно, при частотной модуляции амплитуда и фаза несущего сигнала остаются постоянными. Это может быть лучше понято при соблюдении следующих рисунков.

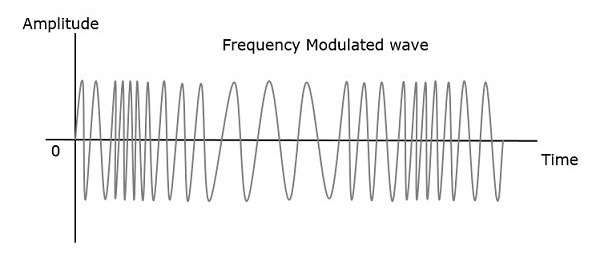
Частота модулированной волны увеличивается, когда амплитуда модулирующего сигнала или сигнала увеличивается. Аналогично, частота модулированной волны уменьшается, когда амплитуда модулирующего сигнала уменьшается. Отметим, что частота модулированной волны остается постоянной и равна частоте несущего сигнала, когда амплитуда модулирующего сигнала равна нулю.

Математическое представление

Уравнение для мгновенной частоты $f_i$ в ЧМ модуляции

$$f_i = f_c + k_fm \ left (t \ right)$$

Куда,

$f_c$ — частота несущей

$k_t$ — частотная чувствительность

$m \ left (t \ right)$ — сигнал сообщения

Мы знаем соотношение между угловой частотой $\ omega_i$ и углом $\ theta _i \ left (t \ right)$ как

$$\ omega_i = \ frac {d \ theta _i \ left (t \ right)} {dt}$$

$\ Rightarrow 2 \ pi f_i = \ frac {d \ theta _i \ left (t \ right)} {dt}$

$\ Rightarrow \ theta _i \ left (t \ right) = 2 \ pi \ int f_i dt$

Замените значение $f_i$ в приведенном выше уравнении.

$$\ theta _i \ left (t \ right) = 2 \ pi \ int \ left (f_c + k_f m \ left (t \ right) \ right) dt$$

$\ Rightarrow \ theta _i \ left (t \ right) = 2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt$

Подставьте значение $\ theta _i \ left (t \ right)$ в стандартное уравнение волны с угловой модуляцией.

$$s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right)$$

Это уравнение FM-волны .

Если модулирующий сигнал равен $m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right)$, то уравнение FM-волны будет

$$s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ sin \ left (2 \ pi f_mt \ right) \ right)$$

Куда,

$\ beta$ = индекс модуляции $= \ frac {\ Delta f} {f_m} = \ frac {k_fA_m} {f_m}$

Разница между FM-модулированной частотой (мгновенной частотой) и нормальной несущей частотой называется отклонением частоты . Он обозначается через $\ Delta f$, который равен произведению $k_f$ и $A_m$.

ЧМ можно разделить на узкополосный ЧМ и широкополосный ЧМ по значениям индекса модуляции $\ beta$.

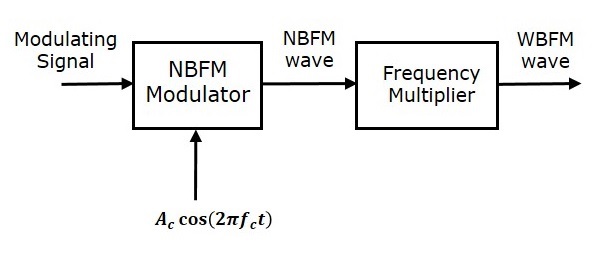
Узкополосный FM

Ниже приведены особенности узкополосного FM.

• Эта частотная модуляция имеет небольшую ширину полосы по сравнению с широкополосной ЧМ.

• Индекс модуляции $\ beta$ мал, т. Е. Меньше 1.

• Его спектр состоит из несущей, верхней боковой полосы и нижней боковой полосы.

• Это используется в мобильной связи, такой как полицейская радиосвязь, машины скорой помощи, такси и т. Д.

Эта частотная модуляция имеет небольшую ширину полосы по сравнению с широкополосной ЧМ.

Индекс модуляции $\ beta$ мал, т. Е. Меньше 1.

Его спектр состоит из несущей, верхней боковой полосы и нижней боковой полосы.

Это используется в мобильной связи, такой как полицейская радиосвязь, машины скорой помощи, такси и т. Д.

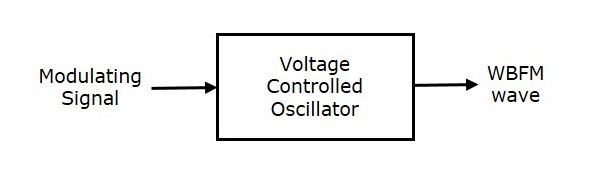
Широкополосный FM

Ниже приведены особенности широкополосного FM.

• Эта частотная модуляция имеет бесконечную полосу пропускания.

• Индекс модуляции $\ beta$ большой, т. Е. Выше 1.

• Его спектр состоит из несущей и бесконечного количества боковых полос, которые расположены вокруг него.

• Это используется в развлекательных, вещательных приложениях, таких как FM-радио, ТВ и т. Д.

Эта частотная модуляция имеет бесконечную полосу пропускания.

Индекс модуляции $\ beta$ большой, т. Е. Выше 1.

Его спектр состоит из несущей и бесконечного количества боковых полос, которые расположены вокруг него.

Это используется в развлекательных, вещательных приложениях, таких как FM-радио, ТВ и т. Д.

Фазовая модуляция

В частотной модуляции частота несущей изменяется. Принимая во внимание, что в фазовой модуляции (PM) фаза несущего сигнала изменяется в соответствии с мгновенной амплитудой модулирующего сигнала.

Таким образом, при фазовой модуляции амплитуда и частота несущего сигнала остаются постоянными. Это может быть лучше понято при соблюдении следующих рисунков.

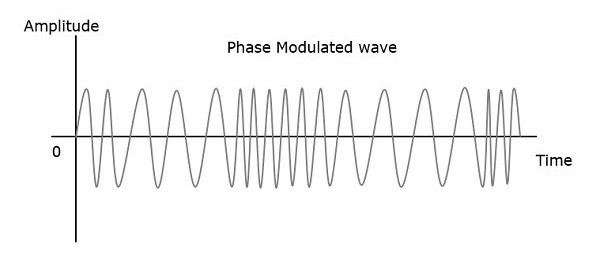
Фаза модулированной волны имеет бесконечные точки, в которых может иметь место фазовый сдвиг в волне. Мгновенная амплитуда модулирующего сигнала изменяет фазу несущего сигнала. Когда амплитуда положительна, фаза изменяется в одном направлении, а если амплитуда отрицательна, фаза изменяется в противоположном направлении.

Математическое представление

Уравнение для мгновенной фазы $\ phi_i$ в фазовой модуляции

$$\ phi _i = k_p m \ left (t \ right)$$

Куда,

• $k_p$ — фазовая чувствительность

• $m \ left (t \ right)$ — сигнал сообщения

$k_p$ — фазовая чувствительность

$m \ left (t \ right)$ — сигнал сообщения

Стандартное уравнение угловой модуляции волны

$$s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ phi_i \ right)$$

Замените значение $\ phi_i$ в приведенном выше уравнении.

$$s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + k_p m \ left (t \ right) \ right)$$

Это уравнение волны ПМ .

Если модулирующий сигнал $m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right)$, то уравнение волны PM будет иметь вид

$$s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ cos \ left (2 \ pi f_mt \ right) \ right)$$

Куда,

• $\ beta$ = индекс модуляции = $\ Delta \ phi = k_pA_m$

• $\ Delta \ phi$ — девиация фазы

$\ beta$ = индекс модуляции = $\ Delta \ phi = k_pA_m$

$\ Delta \ phi$ — девиация фазы

Фазовая модуляция используется в системах мобильной связи, в то время как частотная модуляция используется главным образом для FM-вещания.

Численные задачи 2

В предыдущей главе мы обсудили параметры, используемые в угловой модуляции. Каждый параметр имеет свою формулу. Используя эти формулы, мы можем найти соответствующие значения параметров. В этой главе давайте решим несколько проблем, основанных на концепции частотной модуляции.

Проблема 1

Синусоидальный модулирующий сигнал с амплитудой 5 В и частотой 2 кГц подается на ЧМ-генератор, который имеет частотную чувствительность 40 Гц / вольт. Рассчитайте отклонение частоты, индекс модуляции и ширину полосы.

Решение

Дана амплитуда модулирующего сигнала, $A_m = 5V$

Частота модулирующего сигнала, $f_m = 2 кГц$

Чувствительность по частоте, $k_f = 40 Гц / вольт$

Мы знаем формулу для отклонения частоты как

$$\ Delta f = k_f A_m$$

Замените значения $k_f$ и $A_m$ в приведенной выше формуле.

$$\ Delta f = 40 \ times 5 = 200 Гц$$

Следовательно, отклонение частоты , $\ Delta f$, составляет $ 200 Гц.

Формула для индекса модуляции

$$\ beta = \ frac {\ Delta f} {f_m}$$

Подставьте значения $\ Delta f$ и $f_m$ в приведенной выше формуле.

$$\ beta = \ frac {200} {2 \ times 1000} = 0.1$$

Здесь значение индекса модуляции $\ beta$ равно 0,1, что меньше единицы. Следовательно, это узкополосный FM.

Формула для полосы пропускания узкополосного ЧМ такая же, как и для волны AM.

$$BW = 2f_m$$

Замените значение $f_m$ в приведенной выше формуле.

$$BW = 2 \ times 2K = 4 кГц$$

Следовательно, ширина полосы частот узкополосной ЧМ волны составляет 4 кГц.

Проблема 2

Волна ЧМ определяется как $s \ left (t \ right) = 20 \ cos \ left (8 \ pi \ times10 ^ 6t + 9 \ sin \ left (2 \ pi \ times 10 ^ 3 t \ right) \ right )$. Рассчитайте отклонение частоты, ширину полосы и мощность FM-волны.

Решение

Учитывая, уравнение FM-волны как

$$s \ left (t \ right) = 20 \ cos \ left (8 \ pi \ times10 ^ 6t + 9 \ sin \ left (2 \ pi \ times 10 ^ 3 t \ right) \ right)$$

Мы знаем стандартное уравнение FM-волны как

$$s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ sin \ left (2 \ pi f_mt \ right) \ right)$$

Мы получим следующие значения, сравнивая два приведенных выше уравнения.

Амплитуда несущего сигнала, $A_c = 20 В$

Частота несущего сигнала, $f_c = 4 \ 10 × 6 Гц = 4 МГц$

Частота сигнала сообщения, $f_m = 1 \ умножение на 10 ^ 3 Гц = 1 кГц$

Индекс модуляции, $\ beta = 9$

Здесь значение индекса модуляции больше единицы. Следовательно, это широкополосный FM .

Мы знаем формулу для индекса модуляции как

$$\ beta = \ frac {\ Delta f} {f_m}$$

Переставьте приведенное выше уравнение следующим образом.

$$\ Delta = \ beta f_m$$

Замените значения $\ beta$ и $f_m$ в приведенном выше уравнении.

$$\ Delta = 9 \ times 1K = 9 кГц$$

Следовательно, отклонение частоты $\ Delta f$ составляет $ 9 кГц.

Формула для полосы пропускания широкополосной FM-волны

$$BW = 2 \ left (\ beta +1 \ right) f_m$$

Замените значения $\ beta$ и $f_m$ в приведенной выше формуле.

$$BW = 2 \ left (9 +1 \ right) 1K = 20 кГц$$

Таким образом, полоса пропускания широкополосной FM-волны составляет 20 кГц.

Формула для мощности FM-волны

$$P_c = \ frac {{A_ {c}} ^ {2}} {2R}$$

Предположим, $R = 1 \ Omega$ и подставим значение $A_c$ в вышеприведенное уравнение.

$$P = \ frac {\ left (20 \ right) ^ 2} {2 \ left (1 \ right)} = 200 Вт$$

Следовательно, мощность FM-волны составляет 200 долларов США.

Аналоговая связь — FM модуляторы

В этой главе давайте поговорим о модуляторах, которые генерируют волны NBFM и WBFM. Во-первых, давайте поговорим о поколении NBFM.

Поколение NBFM

Мы знаем, что стандартное уравнение FM-волны

$$s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right)$$

$\ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi k_f \ int m \ left (t \ right) dt \ right) -$

$A_c \ sin \ left (2 \ pi f_ct \ right) \ sin \ left (2 \ pi k_f \ int m \ left (t \ right) dt \ right)$

Для НБФМ,

$$ \ left | 2 \ pi k_f \ int m \ left (t \ right) dt \ right | <<1 $$

Мы знаем, что $\ cos \ theta \ ок 1$ и $\ sin \ theta \ ок 1$, когда $\ theta$ очень мало.

Используя приведенные выше соотношения, мы получим уравнение НБФМ как

$$s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) -A_c \ sin \ left (2 \ pi f_ct \ right) 2 \ pi k_f \ int m \ left (t \ справа) dt$$

Блок-схема модулятора NBFM показана на следующем рисунке.

Здесь интегратор используется для интегрирования модулирующего сигнала $m \ left (t \ right)$. Сигнал несущей $A_c \ cos \ left (2 \ pi f_ct \ right)$ — это сдвинутая по фазе фаза на $-90 ^ 0$, чтобы получить $A_c \ sin \ left (2 \ pi f_ct \ right)$ с помощью $-90 ^ 0$ фазовращатель. Модулятор произведения имеет два входа: $\ int m \ left (t \ right) dt$ и $A_c \ sin \ left (2 \ pi f_ct \ right)$. Он производит вывод, который является произведением этих двух входов.

Это дополнительно умножается на $2 \ pi k_f$, помещая блок $2 \ pi k_f$ в прямой путь. Летний блок имеет два входа, которые являются не чем иным, как двумя членами уравнения NBFM. Положительные и отрицательные знаки присваиваются сигналу несущей, а другой член на входе летнего блока. Наконец, летний блок производит волну NBFM.

Поколение WBFM

Следующие два метода генерируют волну WBFM.

• Прямой метод
• Косвенный метод

Прямой метод

Этот метод называется прямым методом, потому что мы генерируем широкополосную ЧМ волну напрямую. В этом методе генератор напряжения, управляемый напряжением (VCO), используется для генерации WBFM. ГУН выдает выходной сигнал, частота которого пропорциональна напряжению входного сигнала. Это похоже на определение FM-волны. Блок-схема генерации волны WBFM показана на следующем рисунке.

Здесь модулирующий сигнал $m \ left (t \ right)$ применяется в качестве входа генератора, управляемого напряжением (VCO). VCO производит вывод, который является ничем иным, как WBFM.

$$f_i \: \ alpha \: m \ left (t \ right)$$

$$\ Rightarrow f_i = f_c + k_fm \ left (t \ right)$$

Куда,

$f_i$ — мгновенная частота волны WBFM.

Косвенный метод

Этот метод называется косвенным методом, потому что мы генерируем широкополосную ЧМ волну косвенно. Это означает, что сначала мы сгенерируем волну NBFM, а затем с помощью множителей частоты получим волну WBFM. Блок-схема генерации волны WBFM показана на следующем рисунке.

Эта блок-схема содержит в основном два этапа. На первом этапе волна NBFM будет генерироваться с использованием модулятора NBFM. Мы видели блок-схему модулятора NBFM в начале этой главы. Мы знаем, что индекс модуляции волны NBFM меньше единицы. Следовательно, чтобы получить требуемый индекс модуляции (больше единицы) FM-волны, правильно выберите значение множителя частоты.

Множитель частоты — это нелинейное устройство, которое генерирует выходной сигнал, частота которого в n раз превышает частоту входного сигнала. Где ‘n’ — коэффициент умножения.

Если волна NBFM, чей индекс модуляции $\ beta$ меньше 1, применяется в качестве входа умножителя частоты, то умножитель частоты создает выходной сигнал, чей индекс модуляции равен n раз $\ beta$, а частота также равна n раз частота волны WBFM.

Иногда нам может потребоваться несколько ступеней умножителя частоты и смесителей, чтобы увеличить отклонение частоты и индекс модуляции FM-волны.

Аналоговая связь — FM-демодуляторы

В этой главе давайте поговорим о демодуляторах, которые демодулируют FM-волну. Следующие два метода демодулируют FM-волну.

• Метод частотной дискриминации
• Метод фазовой дискриминации

Метод частотной дискриминации

Мы знаем, что уравнение FM-волны

$$s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right)$$

Продифференцируйте вышеприведенное уравнение относительно « t »

$$\ frac {ds \ left (t \ right)} {dt} = -A_c \ left (2 \ pi f_c + 2 \ pi k_fm \ left (t \ right) \ right) \ sin \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right)$$

Мы можем написать $- \ sin \ theta$ как $\ sin \ left (\ theta -180 ^ 0 \ right)$.

$$\ Rightarrow \ frac {ds (t)} {dt} = A_c \ left (2 \ pi f_c + 2 \ pi k_fm \ left (t \ right) \ right) \ sin \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt-180 ^ 0 \ right)$$

$$\ Rightarrow \ frac {ds (t)} {dt} = A_c \ left (2 \ pi f_c \ right) \ left [1+ \ left (\ frac {k_f} {k_c} \ right) m \ left ( t \ right) \ right] \ sin \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt-180 ^ 0 \ right)$$

В вышеприведенном уравнении член амплитуды напоминает огибающую волны AM, а член угла напоминает угол волны FM. Здесь нашим требованием является модулирующий сигнал $m \ left (t \ right)$. Следовательно, мы можем восстановить его из оболочки AM-волны.

На следующем рисунке показана блок-схема FM-демодулятора с использованием метода частотной дискриминации.

Эта блок-схема состоит из дифференциатора и детектора огибающей. Дифференциатор используется для преобразования FM-волны в комбинацию AM-волны и FM-волны. Это означает, что он преобразует изменения частоты FM-волны в соответствующие изменения напряжения (амплитуды) AM-волны. Мы знаем, как работает детектор огибающей. Он производит демодулированный выходной сигнал AM-волны, который является не чем иным, как модулирующим сигналом.

Метод фазовой дискриминации

На следующем рисунке показана блок-схема FM-демодулятора с использованием метода фазовой дискриминации.

Эта блок-схема состоит из умножителя, фильтра нижних частот и генератора, управляемого напряжением (VCO). VCO генерирует выходной сигнал $v \ left (t \ right)$, частота которого пропорциональна напряжению входного сигнала $d \ left (t \ right)$. Первоначально, когда сигнал $d \ left (t \ right)$ равен нулю, отрегулируйте VCO, чтобы получить выходной сигнал $v \ left (t \ right)$, имеющий несущую частоту и сдвиг фазы $-90 ^ 0$ по отношению к сигналу несущей.

FM-волна $s \ left (t \ right)$ и выход VCO $v \ left (t \ right)$ применяются в качестве входных данных множителя. Умножитель производит выходной сигнал, имеющий высокочастотную составляющую и низкочастотную составляющую. Фильтр нижних частот устраняет высокочастотную составляющую и выдает только низкочастотную составляющую в качестве своего выхода.

Этот низкочастотный компонент содержит только разность фаз, связанную с термином. Следовательно, мы получаем модулирующий сигнал $m \ left (t \ right)$ с этого выхода фильтра нижних частот.

Аналоговая связь — мультиплексирование

Мультиплексирование — это процесс объединения нескольких сигналов в один сигнал через общую среду. Если аналоговые сигналы мультиплексируются, то это называется аналоговым мультиплексированием . Аналогично, если цифровые сигналы мультиплексируются, то это называется цифровым мультиплексированием .

Мультиплексирование впервые было разработано в телефонии. Ряд сигналов были объединены для отправки по одному кабелю. Процесс мультиплексирования делит канал связи на несколько логических каналов, выделяя каждый канал для другого сигнала сообщения или потока данных для передачи. Устройство, которое выполняет мультиплексирование, может называться мультиплексором или мультиплексором .

Обратный процесс, т. Е. Извлечение количества каналов из одного, что выполняется в приемнике, называется демультиплексированием . Устройство, которое выполняет демультиплексирование, может называться демультиплексором или DEMUX .

Следующие рисунки иллюстрируют концепцию MUX и DEMUX. Их основное использование в области связи.

Типы мультиплексоров

Существует в основном два типа мультиплексоров, а именно аналоговый и цифровой. Они также делятся на мультиплексирование с частотным разделением (FDM), мультиплексирование с разделением по длине волны (WDM) и мультиплексирование с временным разделением (TDM). Следующий рисунок дает подробное представление об этой классификации.

Есть много типов методов мультиплексирования. Из которых у нас есть основные типы с общей классификацией, упомянутые на рисунке выше. Давайте посмотрим на них индивидуально.

Аналоговое мультиплексирование

Сигналы, используемые в методах аналогового мультиплексирования, имеют аналоговый характер. Аналоговые сигналы мультиплексируются в соответствии с их частотой (FDM) или длиной волны (WDM).

Мультиплексирование с частотным разделением

В аналоговом мультиплексировании наиболее часто используемым методом является мультиплексирование с частотным разделением (FDM). Этот метод использует различные частоты для объединения потоков данных, для отправки их на коммуникационную среду, в виде единого сигнала.

Пример . Традиционный телевизионный передатчик, который отправляет несколько каналов по одному кабелю, использует FDM.

Мультиплексирование с разделением по длине волны

Мультиплексирование с разделением по длине волны (WDM) является аналоговым методом, в котором множество потоков данных с различными длинами волн передаются в световом спектре. Если длина волны увеличивается, частота сигнала уменьшается. Призма, которая может превращать волны различной длины в одну линию, может использоваться на выходе MUX и на входе DEMUX.

Пример. В оптоволоконной связи используется метод WDM для объединения различных длин волн в один источник света для связи.

Цифровое мультиплексирование

Термин цифровой представляет дискретные биты информации. Следовательно, доступные данные находятся в форме кадров или пакетов, которые являются дискретными.

Мультиплексирование с временным разделением

В мультиплексировании с временным разделением (TDM) временной интервал делится на временные интервалы. Этот метод используется для передачи сигнала по одному каналу связи путем выделения одного интервала для каждого сообщения.

Мультиплексирование с временным разделением (TDM) можно классифицировать на синхронный TDM и асинхронный TDM.

Синхронный TDM

В синхронном TDM вход подключен к кадру. Если имеется n соединений, то кадр делится на n слотов. Один слот выделяется для каждой входной линии.

В этом методе частота дискретизации является общей для всех сигналов и, следовательно, задается один и тот же тактовый вход. MUX постоянно выделяет один и тот же слот каждому устройству.

Асинхронный TDM

В асинхронном TDM частота дискретизации отличается для каждого из сигналов, и общий тактовый генератор не требуется. Если выделенное устройство для временного интервала ничего не передает и бездействует, то этот интервал может быть выделен другому устройству, в отличие от синхронного

Этот тип TDM используется в сетях с асинхронным режимом передачи.

Де-Мультиплексор

Демультиплексоры используются для подключения одного источника к нескольким получателям. Этот процесс является обратным процессом мультиплексирования. Как упоминалось ранее, он используется в основном на приемниках. DEMUX имеет много применений. Используется в приемниках в системах связи. Он используется в арифметических и логических единицах компьютеров для питания и передачи данных и т. Д.

Демультиплексоры используются как последовательные в параллельные преобразователи. Последовательные данные передаются в DEMUX через регулярные промежутки времени, и к нему присоединяется счетчик для управления выходом демультиплексора.

Как мультиплексоры, так и демультиплексоры играют важную роль в системах связи как в передающей, так и в приемной секциях.

Аналоговая связь — шум

В любой системе связи во время передачи сигнала или во время приема сигнала в связь вводится некоторый нежелательный сигнал, что делает его неприемлемым для приемника и ставит под сомнение качество связи. Такое нарушение называется шумом .

Что такое шум?

Шум является нежелательным сигналом , который мешает исходному сигналу сообщения и искажает параметры сигнала сообщения. Это изменение в процессе коммуникации приводит к изменению сообщения. Скорее всего, он входит в канал или приемник.

Шумовой сигнал можно понять, взглянув на следующий рисунок.

Следовательно, понятно, что шум — это некоторый сигнал, который не имеет шаблона и не имеет постоянной частоты или амплитуды. Это совершенно случайно и непредсказуемо. Обычно принимаются меры по его снижению, хотя это не может быть полностью устранено.

Наиболее распространенные примеры шума —

• Hiss звук в радиоприемниках

• Звук гудения среди телефонных разговоров

• Мерцание в телевизионных приемниках и т. Д.

Hiss звук в радиоприемниках

Звук гудения среди телефонных разговоров

Мерцание в телевизионных приемниках и т. Д.

Типы шума

Классификация шума выполняется в зависимости от типа источника, эффекта, который он показывает, или его отношения с приемником и т. Д.

Существует два основных способа получения шума. Один через некоторый внешний источник, в то время как другой создается внутренним источником внутри секции приемника.

Внешний источник

Этот шум создается внешними источниками, которые обычно могут возникать в среде или канале связи. Этот шум не может быть полностью устранен. Лучший способ — избежать влияния шума на сигнал.

Примеры

Наиболее распространенными примерами этого типа шума являются

• Атмосферный шум (из-за неровностей в атмосфере).

• Внеземной шум, такой как солнечный шум и космический шум.

• Промышленный шум.

Атмосферный шум (из-за неровностей в атмосфере).

Внеземной шум, такой как солнечный шум и космический шум.

Промышленный шум.

Внутренний Источник

Этот шум создается компонентами приемника во время работы. Компоненты в цепях из-за непрерывного функционирования могут создавать несколько типов шума. Этот шум поддается количественной оценке. Правильная конструкция приемника может снизить влияние этого внутреннего шума.

Примеры

Наиболее распространенными примерами этого типа шума являются

• Шум при тепловом возбуждении (шум Джонсона или электрический шум)

• Шум выстрела (из-за случайного движения электронов и дырок)

• Транзитный шум (во время перехода)

• Разные шумы — это другой тип шума, который включает мерцание, эффект сопротивления, шум, создаваемый микшером, и т. Д.

Шум при тепловом возбуждении (шум Джонсона или электрический шум)

Шум выстрела (из-за случайного движения электронов и дырок)

Транзитный шум (во время перехода)

Разные шумы — это другой тип шума, который включает мерцание, эффект сопротивления, шум, создаваемый микшером, и т. Д.

Эффекты шума

Шум является неудобной функцией, которая влияет на производительность системы. Ниже приведены эффекты шума.

Шум ограничивает рабочий диапазон систем

Шум косвенно накладывает ограничение на самый слабый сигнал, который может быть усилен усилителем. Генератор в цепи смесителя может ограничивать свою частоту из-за шума. Работа системы зависит от работы ее цепей. Шум ограничивает наименьший сигнал, который приемник способен обрабатывать.

Шум влияет на чувствительность приемников

Чувствительность — это минимальное количество входного сигнала, необходимое для получения заданного качества на выходе. Шум влияет на чувствительность приемной системы, что в конечном итоге влияет на выход.

Аналоговая связь — расчеты SNR

В этой главе мы рассчитаем соотношение сигнал / шум и показатель качества различных модулированных волн, которые демодулируются в приемнике.

Сигнал-шум

Отношение сигнал / шум (SNR) — это отношение мощности сигнала к мощности шума. Чем выше значение SNR, тем выше будет качество полученного вывода.

Соотношение сигнал / шум в разных точках можно рассчитать по следующим формулам.

Входное SNR = $\ left (SNR \ right) _I = \ frac {Среднее \: \: мощность \: \: of \: \: модулирующий \: \: сигнал} {Среднее \: \: мощность \: \: of \: \: noise \: \: at \: \: input}$

Выходное SNR = $\ left (SNR \ right) _O = \ frac {Среднее \: \: мощность \: \: of \: \: демодулировано \: \: signal} {Среднее \: \: мощность \: \: of \: \: noise \: \: at \: \: output}$

SNR канала = $\ left (SNR \ right) _C = \ frac {Average \: \: power \: \: of \: \: modulated \: \: signal} {Average \: \: power \: \: of \: \: noise \: \: in \: \: message \: \: пропускная способность}$

Фигура заслуги

Соотношение выходного SNR и входного SNR можно обозначить как показатель качества . Обозначается через F. Описывает производительность устройства.

$$F = \ frac {\ left (SNR \ right) _O} {\ left (SNR \ right) _I}$$

Показатель качества приемника

$$F = \ frac {\ left (SNR \ right) _O} {\ left (SNR \ right) _C}$$

Это так, потому что для приемника канал является входом.

Расчет SNR в системе AM

Рассмотрим следующую модель приемника системы AM для анализа шума.

Мы знаем, что волна с амплитудной модуляцией (AM)

$$s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$$

$$\ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right)$$

Средняя мощность волны AM

$$ P_s = \ left (\ frac {A_c} {\ sqrt {2}} \ right) ^ 2 + \ left (\ frac {A_ck_am \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ гидроразрыва {{А_ {C}} ^ {2}} {2} + \ гидроразрыва {{А_ {C}} ^ {2} {к_ {а}} ^ {2} Р} {2} $ $

$$\ Rightarrow P_s = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} P \ right)} {2}$$

Средняя мощность шума в полосе пропускания сообщения

$$Р- {} пс = WN_0$$

Подставим эти значения в формулу SNR канала

$$\ left (SNR \ right) _ {C, AM} = \ frac {Среднее \: \: Мощность \: \: of \: \: AM \: \: Волна} {Средняя \: \: Мощность \: \: of \: \: noise \: \: in \: \: message \: \: пропускная способность}$$

$$\ Rightarrow \ left (SNR \ right) _ {C, AM} = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ right) P } {2WN_0}$$

Куда,

• P — мощность сигнала сообщения = $\ frac {{A_ {m}} ^ {2}} {2}$

• W — пропускная способность сообщения

P — мощность сигнала сообщения = $\ frac {{A_ {m}} ^ {2}} {2}$

W — пропускная способность сообщения

Предположим, что полосовой шум смешан с АМ волной в канале, как показано на рисунке выше. Эта комбинация применяется на входе демодулятора AM. Следовательно, вход AM демодулятора есть.

$$v \ left (t \ right) = s \ left (t \ right) + n \ left (t \ right)$$

$\ Rightarrow v \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) +$

$\ left [n_1 \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right]$

$\ Rightarrow v \ left (t \ right) = \ left [A_c + A_ck_am \ left (t \ right) + n_1 \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right)$

Где $n_I \ left (t \ right)$ и $n_Q \ left (t \ right)$ находятся в фазовой и квадратурной фазовых составляющих шума.

Выход AM-демодулятора — не что иное, как огибающая вышеуказанного сигнала.

$$d \ left (t \ right) = \ sqrt {\ left [A_c + A_cK_am \ left (t \ right) + n_I \ left (t \ right) \ right] ^ 2 + \ left (n_Q \ left (t \ right) \ right) ^ 2}$$

$$\ Rightarrow d \ left (t \ right) \ приблизительно A_c + A_ck_am \ left (t \ right) + n_1 \ left (t \ right)$$

Средняя мощность демодулированного сигнала

$$P_m = \ left (\ frac {A_ck_am \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} {k_ {a} } ^ {2} P} {2}$$

Средняя мощность шума на выходе

$$P_no = WN_0$$

Подставим эти значения в выходную формулу SNR .

$$\ left (SNR \ right) _ {O, AM} = \ frac {Среднее \: \: Мощность \: \: of \: \: демодулировано \: \: signal} {Среднее \: \: Мощность \: \: of \: \: noise \: \: at \: \: Вывод}$$

$$\ Rightarrow \ left (SNR \ right) _ {O, AM} = \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2WN_0}$$

Замените значения на рисунке достоинства формулы AM приемника.

$$F = \ frac {\ left (SNR \ right) _ {O, AM}} {\ left (SNR \ right) _ {C, AM}}$$

$$\ Rightarrow F = \ left (\ frac {{A_ {c} ^ {2}} {k_ {a} ^ {2}} P} {2WN_0} \ right) / \ left (\ frac {{A_ { c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ right) P} {2WN_0} \ right)$$

$$\ Rightarrow F = \ frac {{K_ {a}} ^ {2} P} {1+ {K_ {a}} ^ {2} P}$$

Следовательно, показатель качества приемника AM меньше единицы.

Расчет SNR в системе DSBSC

Рассмотрим следующую модель приемника системы DSBSC для анализа шума.

Мы знаем, что DSBSC модулированная волна

$$s \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right)$$

Средняя мощность DSBSC модулированной волны

$$P_s = \ left (\ frac {A_cm \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {2}$$

Средняя мощность шума в полосе пропускания сообщения

$$Р- {} пс = WN_0$$

Подставим эти значения в формулу SNR канала .

$$\ left (SNR \ right) _ {C, DSBSC} = \ frac {Средний \: \: Мощность \: \: of \: \: DSBSC \: \: модулированный \: \: wave} {Средний \: \: Power \: \: of \: \: noise \: \: in \: \: message \: \: bandwidth}$$

$$\ Rightarrow \ left (SNR \ right) _ {C, DSBSC} = \ frac {{A_ {c}} ^ {2} P} {2WN_0}$$

Предположим, что полосовой шум смешан с модулированной волной DSBSC в канале, как показано на рисунке выше. Эта комбинация применяется в качестве одного из входных данных для модулятора продукта. Следовательно, вход этого продукта модулятора

$$v_1 \ left (t \ right) = s \ left (t \ right) + n \ left (t \ right)$$

$$\ Rightarrow v_1 \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + \ left [n_I \ left (t \ right) \ cos \ left ( 2 \ pi f_ct \ right) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right]$$

$$\ Rightarrow v_1 \ left (t \ right) = \ left [A_cm \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right)$$

Локальный генератор генерирует сигнал несущей $c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right)$. Этот сигнал подается как еще один вход для модулятора продукта. Таким образом, модулятор продукта производит вывод, который является произведением $v_1 \ left (t \ right)$ и $c \ left (t \ right)$.

$$v_2 \ left (t \ right) = v_1 \ left (t \ right) c \ left (t \ right)$$

Подставьте значения $v_1 \ left (t \ right)$ и $c \ left (t \ right)$ в вышеприведенном уравнении.

$$\ Rightarrow v_2 \ left (t \ right) = \ left (\ left [A_cm \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right ) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right) \ cos \ left (2 \ pi f_ct \ right)$$

$$\ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos ^ 2 \ left (2 \ pi f_ct \ right ) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct \ right)$$

$$\ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right] \ left (\ frac {1+ \ cos \ left ( 4 \ pi f_ct \ right)} {2} \ right) -n_Q \ left (t \ right) \ frac {\ sin \ left (4 \ pi f_ct \ right)} {2}$$

Когда вышеуказанный сигнал применяется в качестве входа для фильтра нижних частот, мы получим выход фильтра нижних частот как

$$d \ left (t \ right) = \ frac {\ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right]} {2}$$

Средняя мощность демодулированного сигнала

$$P_m = \ left (\ frac {A_cm \ left (t \ right)} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {8 }$$

Средняя мощность шума на выходе

$$Р- {нет} = \ {гидроразрыва WN_0} {4}$$

Подставим эти значения в выходную формулу SNR .

$$\ left (SNR \ right) _ {O, DSBSC} = \ frac {Среднее \: \: Мощность \: \: of \: \: демодулировано \: \: signal} {Среднее \: \: Мощность \: \: of \: \: noise \: \: at \: \: Вывод}$$

$$\ Rightarrow \ left (SNR \ right) _ {O, DSBSC} = \ left (\ frac {{A_ {c}} ^ {2} P} {8} \ right) / \ left (\ frac {WN_0 } {4} \ right) = \ frac {{A_ {c}} ^ {2} P} {2WN_0}$$

Замените значения на рисунке достоинства формулы приемника DSBSC.

$$F = \ frac {\ left (SNR \ right) _ {O, DSBSC}} {\ left (SNR \ right) _ {C, DSBSC}}$$

$$\ Rightarrow F = \ left (\ frac {{A_ {c}} ^ {2} P} {2WN_0} \ right) / \ left (\ frac {{A_ {c}} ^ {2} P} { 2WN_0} \ right)$$

$$\ Rightarrow F = 1$$

Следовательно, показатель качества приемника DSBSC равен 1.

Расчеты SNR в системе SSBSC

Рассмотрим следующую модель приемника системы SSBSC для анализа шума.

Мы знаем, что модулированная волна SSBSC, имеющая нижнюю боковую полосу,

$$s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right]$$

Средняя мощность SSBSC модулированной волны

$$P_s = \ left (\ frac {A_mA_c} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8}$$

Средняя мощность шума в полосе пропускания сообщения

$$Р- {} пс = WN_0$$

Подставим эти значения в формулу SNR канала .

$$\ left (SNR \ right) _ {C, SSBSC} = \ frac {Средний \: \: Мощность \: \: of \: \: SSBSC \: \: модулированный \: \: wave} {Средний \: \: Power \: \: of \: \: noise \: \: in \: \: message \: \: bandwidth}$$

$$\ Rightarrow \ left (SNR \ right) _ {C, SSBSC} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0}$$

Предположим, что полосовой шум смешан с модулированной волной SSBSC в канале, как показано на рисунке выше. Эта комбинация применяется в качестве одного из входных данных для модулятора продукта. Следовательно, вход этого продукта модулятора

$$v_1 \ left (t \ right) = s \ left (t \ right) + n \ left (t \ right)$$

$$v_1 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] + n_I \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right)$$

Локальный генератор генерирует сигнал несущей $c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right)$. Этот сигнал подается как еще один вход для модулятора продукта. Таким образом, модулятор продукта производит вывод, который является произведением $v_1 \ left (t \ right)$ и $c \ left (t \ right)$.

$$v_2 \ left (t \ right) = v_1 \ left (t \ right) c \ left (t \ right)$$

Подставьте значения $v_1 \ left (t \ right)$ и $c \ left (t \ right)$ в вышеприведенном уравнении.

$\ Rightarrow v_2 (t) = (\ frac {A_mA_c} {2} \ cos [2 \ pi (f_c-f_m) t] + n_I (t) \ cos (2 \ pi f_ct) -$

$n_Q (t) \ sin (2 \ pi f_ct)) \ cos (2 \ pi f_ct)$

$\ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ право) +$

$n_I \ left (t \ right) \ cos ^ 2 \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct \ right)$

$\ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c-f_m \ right) t \ right] + \ cos \ left (2 \ pi f_mt \ right) \ right \} +$

$n_I \ left (t \ right) \ left (\ frac {1+ \ cos \ left (4 \ pi f_ct \ right)} {2} \ right) - n_Q \ left (t \ right) \ frac {\ sin \ left (4 \ pi f_ct \ right)} {2}$

Когда вышеуказанный сигнал применяется в качестве входа для фильтра нижних частот, мы получим выход фильтра нижних частот как

$$d \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left (2 \ pi f_mt \ right) + \ frac {n_I \ left (t \ right)} {2}$$

Средняя мощность демодулированного сигнала

$$P_m = \ left (\ frac {A_mA_c} {4 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32}$$

Средняя мощность шума на выходе

$$Р- {нет} = \ {гидроразрыва WN_0} {4}$$

Подставим эти значения в выходную формулу SNR

$$\ left (SNR \ right) _ {O, SSBSC} = \ frac {Среднее \: \: Мощность \: \: of \: \: демодулировано \: \: signal} {Среднее \: \: Мощность \: \: of \: \: noise \: \: at \: \: output}$$

$$\ Rightarrow \ left (SNR \ right) _ {O, SSBSC} = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} \ right ) / \ left (\ frac {WN_0} {4} \ right) = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0}$$

Замените значения на рисунке достоинства формулы приемника SSBSC

$$F = \ frac {\ left (SNR \ right) _ {O, SSBSC}} {\ left (SNR \ right) _ {C, SSBSC}}$$

$$F = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ right) / \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ right)$$

$$F = 1$$

Следовательно, показатель качества приемника SSBSC равен 1.

Аналоговая связь — передатчики

Антенна, присутствующая в конце секции передатчика, передает модулированную волну. В этой главе давайте поговорим о AM и FM передатчиках.

AM передатчик

AM-передатчик принимает аудиосигнал в качестве входного сигнала и доставляет амплитудно-модулированную волну в антенну в качестве выходного сигнала для передачи. Блок-схема AM-передатчика показана на следующем рисунке.

Работу AM передатчика можно объяснить следующим образом.

• Аудиосигнал с выхода микрофона отправляется на предварительный усилитель, который повышает уровень модулирующего сигнала.

• РЧ генератор генерирует сигнал несущей.

• И модулирующий сигнал, и сигнал несущей передаются на AM модулятор.

• Усилитель мощности используется для увеличения уровня мощности волны AM. Эта волна наконец передается на антенну для передачи.

Аудиосигнал с выхода микрофона отправляется на предварительный усилитель, который повышает уровень модулирующего сигнала.

РЧ генератор генерирует сигнал несущей.

И модулирующий сигнал, и сигнал несущей передаются на AM модулятор.

Усилитель мощности используется для увеличения уровня мощности волны AM. Эта волна наконец передается на антенну для передачи.

FM-передатчик

FM-передатчик — это целое устройство, которое принимает аудиосигнал в качестве входного сигнала и доставляет FM-волну на антенну в качестве выходного сигнала для передачи. Блок-схема FM-передатчика показана на следующем рисунке.

Работу FM-передатчика можно объяснить следующим образом.

• Аудиосигнал с выхода микрофона отправляется на предварительный усилитель, который повышает уровень модулирующего сигнала.

• Этот сигнал затем передается на фильтр верхних частот, который действует как сеть предварительного выделения для фильтрации шума и улучшения отношения сигнал / шум.

• Этот сигнал далее передается в цепь модулятора FM.

• Генераторная схема генерирует высокочастотную несущую, которая отправляется на модулятор вместе с модулирующим сигналом.

• Несколько ступеней умножителя частоты используются для увеличения рабочей частоты. Даже тогда мощности сигнала недостаточно для передачи. Следовательно, РЧ-усилитель мощности используется в конце для увеличения мощности модулированного сигнала. Этот FM-модулированный выходной сигнал наконец передается на антенну для передачи.

Аудиосигнал с выхода микрофона отправляется на предварительный усилитель, который повышает уровень модулирующего сигнала.

Этот сигнал затем передается на фильтр верхних частот, который действует как сеть предварительного выделения для фильтрации шума и улучшения отношения сигнал / шум.

Этот сигнал далее передается в цепь модулятора FM.

Генераторная схема генерирует высокочастотную несущую, которая отправляется на модулятор вместе с модулирующим сигналом.

Несколько ступеней умножителя частоты используются для увеличения рабочей частоты. Даже тогда мощности сигнала недостаточно для передачи. Следовательно, РЧ-усилитель мощности используется в конце для увеличения мощности модулированного сигнала. Этот FM-модулированный выходной сигнал наконец передается на антенну для передачи.

Аналоговая связь — приемники

Антенна, присутствующая в начале секции приемника, принимает модулированную волну. Сначала давайте обсудим требования получателя.

Требования получателя

Приемник AM принимает волну AM и демодулирует ее, используя детектор огибающей. Точно так же FM-приемник принимает FM-волну и демодулирует ее, используя метод дискриминации по частоте. Ниже приведены требования как к AM, так и к FM приемнику.

• Это должно быть экономически эффективным.

• Он должен получать соответствующие модулированные волны.

• Приемник должен иметь возможность настраивать и усиливать нужную станцию.

• Он должен иметь возможность отклонять нежелательные станции.

• Демодуляция должна быть сделана для всех сигналов станции, независимо от частоты несущего сигнала.

Это должно быть экономически эффективным.

Он должен получать соответствующие модулированные волны.

Приемник должен иметь возможность настраивать и усиливать нужную станцию.

Он должен иметь возможность отклонять нежелательные станции.

Демодуляция должна быть сделана для всех сигналов станции, независимо от частоты несущего сигнала.

Чтобы эти требования были выполнены, схема тюнера и схема микшера должны быть очень эффективными. Процедура смешивания RF является интересным явлением.

РЧ микширование

Блок радиочастотного микширования вырабатывает промежуточную частоту (IF), в которую преобразуется любой принятый сигнал, чтобы эффективно обрабатывать сигнал.

РЧ-микшер является важным этапом в приемнике. Два сигнала разных частот принимаются там, где один уровень сигнала влияет на уровень другого сигнала, чтобы получить результирующий смешанный выходной сигнал. Входные сигналы и выходной сигнал микшера показаны на следующих рисунках.

Пусть первая и вторая частоты сигнала равны $f_1$ и $f_2$. Если эти два сигнала применяются в качестве входов радиочастотного микшера, он генерирует выходной сигнал с частотами $f_1 + f_2$ и $f_1-f_2$.

Если это наблюдается в частотной области, шаблон выглядит следующим образом.

В этом случае $f_1$ больше, чем $f_2$. Итак, результирующий вывод имеет частоты $f_1 + f_2$ и $f_1-f_2$. Аналогично, если $f_2$ больше, чем $f_1$, то результирующий вывод будет иметь частоты $f_1 + f_2$ и $f_1-f_2$.

Приемник AM

Супергетеродинный приемник AM принимает амплитудно-модулированную волну в качестве входного сигнала и выдает исходный аудиосигнал в качестве выходного. Избирательность — это способность выбирать определенный сигнал, отвергая при этом другие. Чувствительность — это способность обнаруживать РЧ-сигнал и демодулировать его при минимальном уровне мощности.

Радиолюбители — первые радиоприемники. Однако они имеют недостатки, такие как низкая чувствительность и селективность. Чтобы преодолеть эти недостатки, был изобретен супергетеродинный приемник. Блок-схема AM-приемника показана на следующем рисунке.

Секция радиочастотного тюнера

Волна с амплитудной модуляцией, принятая антенной, сначала передается в схему тюнера через трансформатор. Схема тюнера — это не что иное, как цепь LC, которая также называется резонансной или емкостной цепью . Он выбирает частоту, желаемую приемником AM. Он также настраивает местный генератор и РЧ-фильтр одновременно.

РЧ-микшер

Сигнал с выхода тюнера отправляется на преобразователь RF-IF , который действует как микшер. Он имеет местный генератор, который вырабатывает постоянную частоту. Процесс микширования выполняется здесь, принимая принятый сигнал в качестве одного входа и частоту гетеродина в качестве другого входа. Результирующий вывод представляет собой смесь двух частот $\ left [\ left (f_1 + f_2 \ right), \ left (f_1-f_2 \ right) \ right]$, создаваемых микшером, который называется промежуточной частотой (IF). )

Производство IF помогает в демодуляции любого сигнала станции, имеющего любую несущую частоту. Следовательно, все сигналы преобразуются в фиксированную несущую частоту для адекватной селективности.

ЕСЛИ фильтр

Промежуточный частотный фильтр представляет собой полосовой фильтр, который пропускает желаемую частоту. Это устраняет все другие нежелательные частотные компоненты, присутствующие в нем. Это преимущество фильтра ПЧ, который допускает только частоту ПЧ.

AM Демодулятор

Полученная AM-волна демодулируется с помощью AM-демодулятора. Этот демодулятор использует процесс обнаружения огибающей для получения модулирующего сигнала.

Аудио усилитель

Это каскад усилителя мощности, который используется для усиления обнаруженного аудиосигнала. Обработанный сигнал усиливается, чтобы быть эффективным. Этот сигнал передается на громкоговоритель для получения исходного звукового сигнала.

FM-приемник

Блок-схема FM-приемника показана на следующем рисунке.

Эта структурная схема FM-приемника аналогична структурной схеме AM-приемника. Два блока ограничителя амплитуды и сети снижения акцента включены до и после FM-демодулятора. Работа остальных блоков такая же, как и у AM-приемника.

Мы знаем, что в ЧМ модуляции амплитуда ЧМ волны остается постоянной. Однако, если в канале добавляется шум с FM-волной, амплитуда FM-волны может изменяться. Таким образом, с помощью ограничителя амплитуды мы можем поддерживать амплитуду ЧМ волны постоянной, удаляя нежелательные пики шумового сигнала.

В FM-передатчике мы видели сеть предварительного выделения (фильтр верхних частот), которая присутствует до FM-модулятора. Это используется для улучшения SNR высокочастотного аудиосигнала. Обратный процесс предварительного акцентирования известен как де-акцент . Таким образом, в этом FM-приемнике сеть с понижением выделения (фильтр нижних частот) включена после FM-демодулятора. Этот сигнал передается на аудиоусилитель для повышения уровня мощности. Наконец, мы получаем оригинальный звуковой сигнал от динамика.

Аналоговая связь — выборка

До сих пор мы говорили о непрерывно-волновой модуляции. Мы обсудим импульсную модуляцию в следующей главе. Эти методы импульсной модуляции имеют дело с дискретными сигналами. Итак, теперь давайте посмотрим, как преобразовать непрерывный сигнал времени в дискретный.

Процесс преобразования непрерывных сигналов времени в эквивалентные дискретные сигналы времени можно назвать дискретизацией . Определенный момент данных постоянно отбирается в процессе выборки.

На следующем рисунке показан непрерывный сигнал x (t) и соответствующий дискретизированный сигнал x _s (t) . Когда x (t) умножается на периодическую последовательность импульсов, получается дискретный сигнал x _s (t) .

Сигнал дискретизации представляет собой периодическую последовательность импульсов, имеющих единичную амплитуду, дискретизированную с равными интервалами времени $T_s$, которая называется временем дискретизации . Эти данные передаются в моменты времени $T_s$, а сигнал несущей передается в оставшееся время.

Частота выборки

Чтобы дискретизировать сигналы, промежуток между выборками должен быть исправлен. Этот разрыв можно назвать периодом выборки $T_s$. Взаимное значение периода выборки известно как частота выборки или частота выборки $f_s$ .

Математически мы можем записать это как

$$f_s = \ frac {1} {T_s}$$

Куда,

$f_s$ — частота дискретизации или частота дискретизации.

$T_s$ — период выборки

Теорема выборки

Частота дискретизации должна быть такой, чтобы данные в сигнале сообщения не терялись и не перекрывались. Теорема выборки гласит, что «сигнал может быть точно воспроизведен, если он дискретизирован со скоростью $f_s$, которая больше или равна удвоенной максимальной частоте данного сигнала W ».

Математически мы можем записать это как

$$f_s \ geq 2W$$

Куда,

• $f_s$ — частота выборки

• $W$ — самая высокая частота данного сигнала

$f_s$ — частота выборки

$W$ — самая высокая частота данного сигнала

Если частота дискретизации равна удвоенной максимальной частоте данного сигнала W, то она называется частотой Найквиста .

Теорема отсчетов, которая также называется теоремой Найквиста , дает теорию достаточной частоты дискретизации в терминах полосы пропускания для класса функций с ограниченной полосой пропускания.

Для сигнала непрерывного времени x (t) , который ограничен полосой частот в частотной области, представлен, как показано на следующем рисунке.

Если сигнал дискретизирован выше частоты Найквиста, то исходный сигнал может быть восстановлен. На следующем рисунке поясняется сигнал, если он дискретизируется с более высокой скоростью, чем 2 Вт в частотной области.

Если один и тот же сигнал дискретизируется со скоростью менее 2 Вт , тогда дискретизированный сигнал будет выглядеть следующим образом.

Из приведенного выше паттерна мы можем наблюдать, что информация пересекается, что приводит к смешению и потере информации. Это нежелательное явление перекрытия называется Aliasing .

Псевдоним может быть назван «явлением высокочастотного компонента в спектре сигнала, принимающего идентичность низкочастотного компонента в спектре его дискретизированной версии».

Следовательно, частота дискретизации сигнала выбирается равной частоте Найквиста. Если частота дискретизации равна удвоенной максимальной частоте данного сигнала W , тогда дискретизированный сигнал будет выглядеть следующим образом.

В этом случае сигнал может быть восстановлен без потерь. Следовательно, это хорошая частота дискретизации.

Аналоговая связь — импульсная модуляция

После непрерывной волновой модуляции следующим делением является импульсная модуляция. В этой главе мы обсудим следующие методы аналоговой импульсной модуляции.

• Импульсная амплитудная модуляция
• Широтно-импульсная модуляция
• Импульсная модуляция положения

Импульсная амплитудная модуляция

В методе импульсной амплитудной модуляции (PAM) амплитуда несущей импульса изменяется, которая пропорциональна мгновенной амплитуде сигнала сообщения.

Сигнал с амплитудной модуляцией импульса будет следовать амплитуде исходного сигнала, поскольку сигнал отслеживает путь всей волны. В естественном PAM сигнал, выбранный с частотой Найквиста, можно восстановить, пропустив его через эффективный фильтр нижних частот (LPF) с точной частотой среза.

На следующих рисунках показана амплитудно-импульсная модуляция.

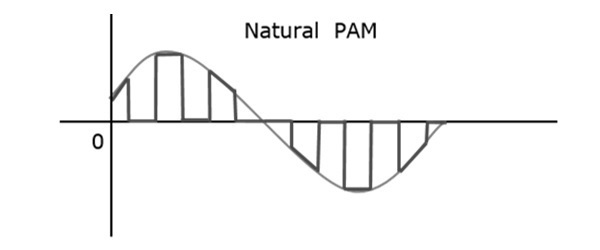
Хотя сигнал PAM пропускается через ФНЧ, он не может восстановить сигнал без искажений. Следовательно, чтобы избежать этого шума, используйте выборку с плоским верхом. Сигнал PAM с плоским верхом показан на следующем рисунке.

Выборка с плоским верхом — это процесс, в котором дискретизированный сигнал может быть представлен в импульсах, для которых амплитуду сигнала нельзя изменить по отношению к аналоговому сигналу, который должен быть дискретизирован. Вершины амплитуды остаются плоскими. Этот процесс упрощает конструкцию схемы.

Широтно-импульсная модуляция

В методах широтно-импульсной модуляции (ШИМ) или длительности импульсной модуляции (PDM) или методики импульсной временной модуляции (ПТМ) ширина, длительность или время несущей импульса изменяются, что пропорционально мгновенной амплитуде сигнала сообщения.

Ширина импульса варьируется в этом методе, но амплитуда сигнала остается постоянной. Ограничители амплитуды используются, чтобы сделать амплитуду сигнала постоянной. Эти схемы обрезают амплитуду до желаемого уровня, и, следовательно, шум ограничен.

На следующем рисунке показаны типы широтно-импульсных модуляций.

Существует три типа ШИМ.

• Постоянный передний фронт импульса, задний фронт изменяется в зависимости от сигнала сообщения. Форма волны для этого типа ШИМ обозначена как (а) на рисунке выше.

• Задний фронт импульса постоянен, передний фронт изменяется в зависимости от сигнала сообщения. Форма волны для этого типа ШИМ обозначена как (b) на рисунке выше.

• Центр импульса является постоянным, передний фронт и задний фронт меняются в зависимости от сигнала сообщения. Форма волны для этого типа ШИМ обозначена как (с), как показано на рисунке выше.

Постоянный передний фронт импульса, задний фронт изменяется в зависимости от сигнала сообщения. Форма волны для этого типа ШИМ обозначена как (а) на рисунке выше.

Задний фронт импульса постоянен, передний фронт изменяется в зависимости от сигнала сообщения. Форма волны для этого типа ШИМ обозначена как (b) на рисунке выше.

Центр импульса является постоянным, передний фронт и задний фронт меняются в зависимости от сигнала сообщения. Форма волны для этого типа ШИМ обозначена как (с), как показано на рисунке выше.

Импульсная модуляция положения

Импульсная модуляция положения (PPM) — это схема аналоговой модуляции, в которой амплитуда и ширина импульсов поддерживаются постоянными, в то время как положение каждого импульса относительно позиции эталонного импульса изменяется в соответствии с мгновенным значением выборки сигнал сообщения.

Передатчик должен посылать синхронизирующие импульсы (или просто синхронизировать импульсы), чтобы поддерживать синхронизацию передатчика и приемника. Эти синхронизирующие импульсы помогают поддерживать положение импульсов. На следующих рисунках показана модуляция положения импульса.

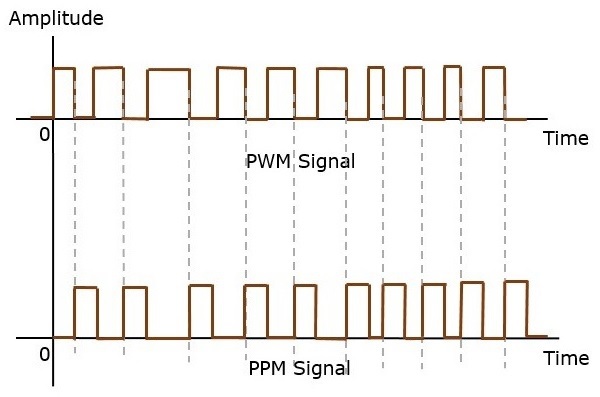
Позиционная модуляция импульса выполняется в соответствии с широтно-импульсным сигналом. Каждый задний фронт сигнала с широтно-импульсной модуляцией становится отправной точкой для импульсов в сигнале PPM. Следовательно, положение этих импульсов пропорционально ширине импульсов ШИМ.

преимущество

Поскольку амплитуда и ширина являются постоянными, мощность, которую обрабатывают, также является постоянной.

Недостаток

Синхронизация между передатчиком и приемником является обязательной.

Сравнение PAM, PWM и PPM

В следующей таблице представлено сравнение между тремя методами модуляции.

РАМ	PWM	PPM
Амплитуда варьируется	Ширина варьируется	Положение варьируется
Пропускная способность зависит от ширины импульса	Пропускная способность зависит от времени нарастания импульса	Пропускная способность зависит от времени нарастания импульса
Мгновенная мощность передатчика зависит от амплитуды импульсов	Мгновенная мощность передатчика зависит от амплитуды и ширины импульсов	Мгновенная мощность передатчика остается постоянной с шириной импульсов
Сложность системы высокая	Сложность системы низкая	Сложность системы низкая
Уровень шума высок	Уровень шума низкий	Уровень шума низкий
Это похоже на амплитудную модуляцию	Это похоже на частотную модуляцию	Это похоже на фазовую модуляцию

Аналоговая связь — преобразователи

Преобразователь — это устройство, которое преобразует энергию из одной формы в другую. В этой главе давайте поговорим о преобразователях, используемых в системах связи.

Зачем нам нужны датчики?

В реальном мире общение между любыми двумя близкими людьми происходит с помощью звуковых волн. Но если люди находятся далеко, то трудно передать информацию без потерь, используя звуковые волны в ее физической форме.

Чтобы преодолеть эту трудность, мы можем использовать модуляторы в секции передатчика и демодуляторы в секции приемника. Эти модуляторы и демодуляторы работают с электрическими сигналами. Вот почему нам требуется устройство, которое должно преобразовывать звуковые волны в электрические сигналы или наоборот. Это устройство известно как преобразователь.

Ниже приведена простая блок-схема преобразователя.

Этот преобразователь имеет один вход и один выход. Он преобразует энергию, присутствующую на входе, в эквивалентный выход, имеющий другую энергию. По сути, преобразователь преобразует неэлектрическую форму энергии в электрическую форму или наоборот.

Типы преобразователей

Мы можем классифицировать преобразователи по следующим двум типам в зависимости от расположения (положения) преобразователя в системах связи.

• Входной преобразователь
• Выходной преобразователь

Входные преобразователи

Датчик, присутствующий на входе системы связи, называется входным датчиком . Ниже приведена блок-схема входного преобразователя.

Этот входной преобразователь преобразует неэлектрическую физическую величину в электрический сигнал. С помощью этого преобразователя физические величины, такие как звук или свет, могут быть преобразованы в электрические величины, такие как напряжение или ток. Пример : микрофон.

Микрофон используется в качестве входного преобразователя, который расположен между источником информации и секцией передатчика. Источник информации производит информацию в форме звуковых волн. Микрофон преобразует эти звуковые волны в электрические сигналы с помощью диафрагмы. Эти электрические сигналы могут быть использованы для дальнейшей обработки.

Выходные преобразователи

Преобразователь, присутствующий на выходе системы связи, известен как выходной преобразователь. Ниже приведена блок-схема выходного преобразователя .

Этот выходной преобразователь преобразует электрический сигнал в неэлектрическую физическую величину. С помощью этого преобразователя электрические величины, такие как напряжение или ток, могут быть преобразованы в физические величины, такие как звук или свет. Пример : громкоговоритель.

Громкоговоритель используется в качестве выходного преобразователя, который расположен между секцией приемника и местом назначения. Демодулятор, присутствующий в секции приемника, производит демодулированный выходной сигнал. Таким образом, громкоговоритель преобразует электрические сигналы (демодулированный выход) в звуковые волны. Следовательно, функциональность громкоговорителя прямо противоположна функциональности микрофона.

В дополнение к вышеупомянутым преобразователям существует еще один преобразователь, который используется в системах связи. Этот преобразователь может быть размещен либо в конце секции передатчика, либо в начале секции приемника. Пример : антенна.

Антенна — это преобразователь, который преобразует электрические сигналы в электромагнитные волны и наоборот. Антенна может использоваться как в качестве передающей антенны, так и в качестве приемной антенны .

Передающая антенна преобразует электрические сигналы в электромагнитные волны и излучает их. При этом приемная антенна преобразует электромагнитные волны из принятого луча в электрические сигналы.

В этой двусторонней связи одна и та же антенна может использоваться как для передачи, так и для приема.