Аналоговая связь — модуляторы SSBSC

В этой главе давайте поговорим о модуляторах, которые генерируют волну SSBSC. Мы можем генерировать волну SSBSC, используя следующие два метода.

• Метод частотной дискриминации
• Метод фазовой дискриминации

Метод частотной дискриминации

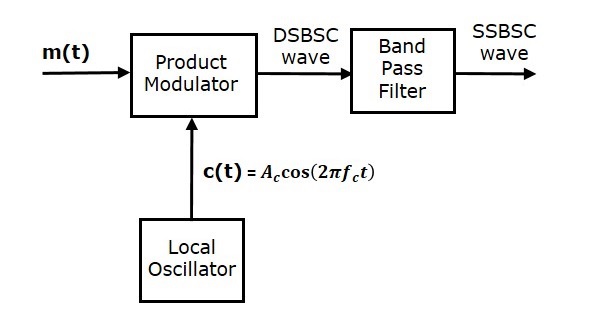
На следующем рисунке показана блок-схема модулятора SSBSC с использованием метода частотной дискриминации.

В этом методе сначала мы сгенерируем волну DSBSC с помощью модулятора продукта. Затем примените эту волну DSBSC в качестве входа полосового фильтра. Этот полосовой фильтр производит выходной сигнал, который является волной SSBSC.

Выберите диапазон частот полосового фильтра в качестве спектра желаемой волны SSBSC. Это означает, что полосовой фильтр можно настроить на частоты либо верхней, либо нижней боковой полосы, чтобы получить соответствующую волну SSBSC, имеющую верхнюю или нижнюю боковую полосу.

Метод фазовой дискриминации

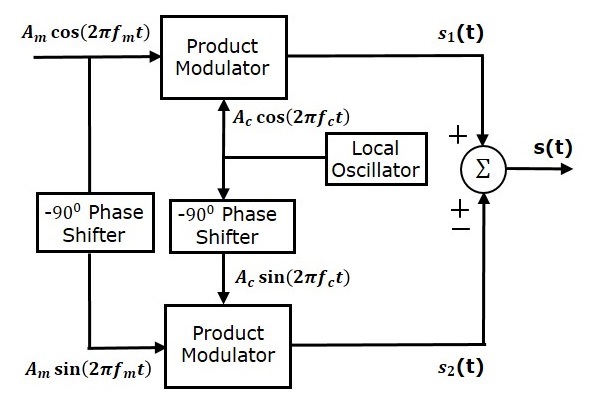
На следующем рисунке показана блок-схема модулятора SSBSC с использованием метода фазовой дискриминации.

Эта блок-схема состоит из двух модуляторов произведений, двух $-90 ^ 0$ фазовращателей, одного локального генератора и одного летнего блока. Модулятор продукта производит выход, который является произведением двух входов. Фазовращатель $-90 ^ 0$ создает выходной сигнал, который имеет фазовую задержку $-90 ^ 0$ относительно входа.

Локальный генератор используется для генерации сигнала несущей. Летний блок создает выходной сигнал, который представляет собой либо сумму двух входов, либо разницу двух входов в зависимости от полярности входов.

Модулирующий сигнал $A_m \ cos \ left (2 \ pi f_mt \ right)$ и несущий сигнал $A_c \ cos \ left (2 \ pi f_ct \ right)$ непосредственно применяются в качестве входных данных для модулятора верхнего произведения. Таким образом, верхний модулятор произведений производит результат, который является произведением этих двух входов.

Выход верхнего модулятора произведения

$$s_1 \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt \ right) \ cos \ left (2 \ pi f_ct \ right)$$

$$\ Rightarrow s_1 \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ right \}$$

Модулирующий сигнал $A_m \ cos \ left (2 \ pi f_mt \ right)$ и несущий сигнал $A_c \ cos \ left (2 \ pi f_ct \ right)$ сдвинуты по фазе на $-90 ^ 0$ перед применением в качестве входы в нижний продукт модулятора. Таким образом, модулятор нижнего произведения производит выход, который является произведением этих двух входов.

Выход нижнего продукта модулятора

$$s_2 \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt-90 ^ 0 \ right) \ cos \ left (2 \ pi f_ct-90 ^ 0 \ right)$$

$\ Rightarrow s_2 \ left (t \ right) = A_mA_c \ sin \ left (2 \ pi f_mt \ right) \ sin \ left (2 \ pi f_ct \ right)$

$\ Rightarrow s_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] - \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] \ right \}$

Добавьте $s_1 \ left (t \ right)$ и $s_2 \ left (t \ right)$, чтобы получить модулированную SSBSC волну $s \ left (t \ right)$, имеющую нижнюю боковую полосу.

$s \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ right \} +$

$\ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] - \ cos \ left [2 \ pi \ left (f_c + f_m \) справа) t \ right] \ right \}$

$\ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right]$

Вычтите $s_2 \ left (t \ right)$ из $s_1 \ left (t \ right)$, чтобы получить SSBSC-модулированную волну $s \ left (t \ right)$, имеющую верхнюю боковую полосу.

$s \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ right \} -$

$\ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] - \ cos \ left [2 \ pi \ left (f_c + f_m \) справа) t \ right] \ right \}$

$\ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right]$

Следовательно, при правильном выборе полярностей входов в летнем блоке мы получим волну SSBSC, имеющую верхнюю боковую полосу или нижнюю боковую полосу.