Аналоговая связь — расчеты SNR

В этой главе мы рассчитаем соотношение сигнал / шум и показатель качества различных модулированных волн, которые демодулируются в приемнике.

Сигнал-шум

Отношение сигнал / шум (SNR) — это отношение мощности сигнала к мощности шума. Чем выше значение SNR, тем выше будет качество полученного вывода.

Соотношение сигнал / шум в разных точках можно рассчитать по следующим формулам.

Входное SNR =  left(SNR right)I= fracСреднеемощностьofмодулирующийсигналСреднеемощностьofnoiseatinput$\ left (SNR \ right) _I = \ frac {Среднее \: \: мощность \: \: of \: \: модулирующий \: \: сигнал} {Среднее \: \: мощность \: \: of \: \: noise \: \: at \: \: input}$

Выходное SNR =  left(SNR right)O= fracСреднеемощностьofдемодулированоsignalСреднеемощностьofnoiseatoutput$\ left (SNR \ right) _O = \ frac {Среднее \: \: мощность \: \: of \: \: демодулировано \: \: signal} {Среднее \: \: мощность \: \: of \: \: noise \: \: at \: \: output}$

SNR канала =  left(SNR right)C= fracAveragepowerofmodulatedsignalAveragepowerofnoiseinmessageпропускнаяспособность$\ left (SNR \ right) _C = \ frac {Average \: \: power \: \: of \: \: modulated \: \: signal} {Average \: \: power \: \: of \: \: noise \: \: in \: \: message \: \: пропускная способность}$

Фигура заслуги

Соотношение выходного SNR и входного SNR можно обозначить как показатель качества . Обозначается через F. Описывает производительность устройства.

$$F = \ frac {\ left (SNR \ right) _O} {\ left (SNR \ right) _I}$$

Показатель качества приемника

$$F = \ frac {\ left (SNR \ right) _O} {\ left (SNR \ right) _C}$$

Это так, потому что для приемника канал является входом.

Расчет SNR в системе AM

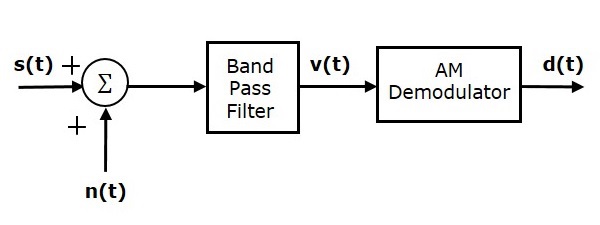
Рассмотрим следующую модель приемника системы AM для анализа шума.

Мы знаем, что волна с амплитудной модуляцией (AM)

$$s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)$$

$$\ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right)$$

Средняя мощность волны AM

$$ P_s = \ left (\ frac {A_c} {\ sqrt {2}} \ right) ^ 2 + \ left (\ frac {A_ck_am \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ гидроразрыва {{А_ {C}} ^ {2}} {2} + \ гидроразрыва {{А_ {C}} ^ {2} {к_ {а}} ^ {2} Р} {2} $ $

$$\ Rightarrow P_s = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} P \ right)} {2}$$

Средняя мощность шума в полосе пропускания сообщения

Р−пс=WN0 $$Р- {} пс = WN_0$$

Подставим эти значения в формулу SNR канала

 left(SNR right)C,AM= fracСреднееМощностьofAMВолнаСредняяМощностьofnoiseinmessageпропускнаяспособность $$\ left (SNR \ right) _ {C, AM} = \ frac {Среднее \: \: Мощность \: \: of \: \: AM \: \: Волна} {Средняя \: \: Мощность \: \: of \: \: noise \: \: in \: \: message \: \: пропускная способность}$$

$$\ Rightarrow \ left (SNR \ right) _ {C, AM} = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ right) P } {2WN_0}$$

Куда,

• P — мощность сигнала сообщения = $\ frac {{A_ {m}} ^ {2}} {2}$

• W — пропускная способность сообщения

P — мощность сигнала сообщения = $\ frac {{A_ {m}} ^ {2}} {2}$

W — пропускная способность сообщения

Предположим, что полосовой шум смешан с АМ волной в канале, как показано на рисунке выше. Эта комбинация применяется на входе демодулятора AM. Следовательно, вход AM демодулятора есть.

$$v \ left (t \ right) = s \ left (t \ right) + n \ left (t \ right)$$

$\ Rightarrow v \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) +$

$\ left [n_1 \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right]$

$\ Rightarrow v \ left (t \ right) = \ left [A_c + A_ck_am \ left (t \ right) + n_1 \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right)$

Где $n_I \ left (t \ right)$ и $n_Q \ left (t \ right)$ находятся в фазовой и квадратурной фазовых составляющих шума.

Выход AM-демодулятора — не что иное, как огибающая вышеуказанного сигнала.

$$d \ left (t \ right) = \ sqrt {\ left [A_c + A_cK_am \ left (t \ right) + n_I \ left (t \ right) \ right] ^ 2 + \ left (n_Q \ left (t \ right) \ right) ^ 2}$$

$$\ Rightarrow d \ left (t \ right) \ приблизительно A_c + A_ck_am \ left (t \ right) + n_1 \ left (t \ right)$$

Средняя мощность демодулированного сигнала

$$P_m = \ left (\ frac {A_ck_am \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} {k_ {a} } ^ {2} P} {2}$$

Средняя мощность шума на выходе

$$P_no = WN_0$$

Подставим эти значения в выходную формулу SNR .

 left(SNR right)O,AM= fracСреднееМощностьofдемодулированоsignalСреднееМощностьofnoiseatВывод $$\ left (SNR \ right) _ {O, AM} = \ frac {Среднее \: \: Мощность \: \: of \: \: демодулировано \: \: signal} {Среднее \: \: Мощность \: \: of \: \: noise \: \: at \: \: Вывод}$$

$$\ Rightarrow \ left (SNR \ right) _ {O, AM} = \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2WN_0}$$

Замените значения на рисунке достоинства формулы AM приемника.

$$F = \ frac {\ left (SNR \ right) _ {O, AM}} {\ left (SNR \ right) _ {C, AM}}$$

$$\ Rightarrow F = \ left (\ frac {{A_ {c} ^ {2}} {k_ {a} ^ {2}} P} {2WN_0} \ right) / \ left (\ frac {{A_ { c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ right) P} {2WN_0} \ right)$$

$$\ Rightarrow F = \ frac {{K_ {a}} ^ {2} P} {1+ {K_ {a}} ^ {2} P}$$

Следовательно, показатель качества приемника AM меньше единицы.

Расчет SNR в системе DSBSC

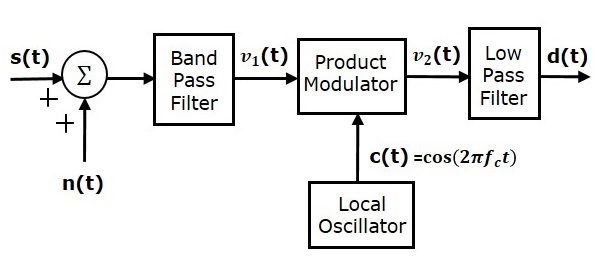
Рассмотрим следующую модель приемника системы DSBSC для анализа шума.

Мы знаем, что DSBSC модулированная волна

$$s \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right)$$

Средняя мощность DSBSC модулированной волны

$$P_s = \ left (\ frac {A_cm \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {2}$$

Средняя мощность шума в полосе пропускания сообщения

Р−пс=WN0 $$Р- {} пс = WN_0$$

Подставим эти значения в формулу SNR канала .

 left(SNR right)C,DSBSC= fracСреднийМощностьofDSBSCмодулированныйwaveСреднийPowerofnoiseinmessagebandwidth $$\ left (SNR \ right) _ {C, DSBSC} = \ frac {Средний \: \: Мощность \: \: of \: \: DSBSC \: \: модулированный \: \: wave} {Средний \: \: Power \: \: of \: \: noise \: \: in \: \: message \: \: bandwidth}$$

$$\ Rightarrow \ left (SNR \ right) _ {C, DSBSC} = \ frac {{A_ {c}} ^ {2} P} {2WN_0}$$

Предположим, что полосовой шум смешан с модулированной волной DSBSC в канале, как показано на рисунке выше. Эта комбинация применяется в качестве одного из входных данных для модулятора продукта. Следовательно, вход этого продукта модулятора

$$v_1 \ left (t \ right) = s \ left (t \ right) + n \ left (t \ right)$$

$$\ Rightarrow v_1 \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + \ left [n_I \ left (t \ right) \ cos \ left ( 2 \ pi f_ct \ right) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right]$$

$$\ Rightarrow v_1 \ left (t \ right) = \ left [A_cm \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right)$$

Локальный генератор генерирует сигнал несущей $c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right)$. Этот сигнал подается как еще один вход для модулятора продукта. Таким образом, модулятор продукта производит вывод, который является произведением $v_1 \ left (t \ right)$ и $c \ left (t \ right)$.

$$v_2 \ left (t \ right) = v_1 \ left (t \ right) c \ left (t \ right)$$

Подставьте значения $v_1 \ left (t \ right)$ и $c \ left (t \ right)$ в вышеприведенном уравнении.

$$\ Rightarrow v_2 \ left (t \ right) = \ left (\ left [A_cm \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right ) - n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right) \ cos \ left (2 \ pi f_ct \ right)$$

$$\ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos ^ 2 \ left (2 \ pi f_ct \ right ) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct \ right)$$

$$\ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right] \ left (\ frac {1+ \ cos \ left ( 4 \ pi f_ct \ right)} {2} \ right) -n_Q \ left (t \ right) \ frac {\ sin \ left (4 \ pi f_ct \ right)} {2}$$

Когда вышеуказанный сигнал применяется в качестве входа для фильтра нижних частот, мы получим выход фильтра нижних частот как

$$d \ left (t \ right) = \ frac {\ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right]} {2}$$

Средняя мощность демодулированного сигнала

$$P_m = \ left (\ frac {A_cm \ left (t \ right)} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {8 }$$

Средняя мощность шума на выходе

$$Р- {нет} = \ {гидроразрыва WN_0} {4}$$

Подставим эти значения в выходную формулу SNR .

$$\ left (SNR \ right) _ {O, DSBSC} = \ frac {Среднее \: \: Мощность \: \: of \: \: демодулировано \: \: signal} {Среднее \: \: Мощность \: \: of \: \: noise \: \: at \: \: Вывод}$$

$$\ Rightarrow \ left (SNR \ right) _ {O, DSBSC} = \ left (\ frac {{A_ {c}} ^ {2} P} {8} \ right) / \ left (\ frac {WN_0 } {4} \ right) = \ frac {{A_ {c}} ^ {2} P} {2WN_0}$$

Замените значения на рисунке достоинства формулы приемника DSBSC.

$$F = \ frac {\ left (SNR \ right) _ {O, DSBSC}} {\ left (SNR \ right) _ {C, DSBSC}}$$

$$\ Rightarrow F = \ left (\ frac {{A_ {c}} ^ {2} P} {2WN_0} \ right) / \ left (\ frac {{A_ {c}} ^ {2} P} { 2WN_0} \ right)$$

$$\ Rightarrow F = 1$$

Следовательно, показатель качества приемника DSBSC равен 1.

Расчеты SNR в системе SSBSC

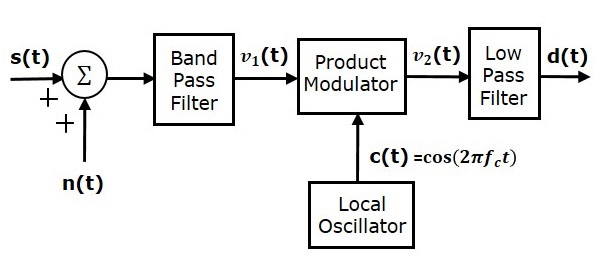
Рассмотрим следующую модель приемника системы SSBSC для анализа шума.

Мы знаем, что модулированная волна SSBSC, имеющая нижнюю боковую полосу,

$$s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right]$$

Средняя мощность SSBSC модулированной волны

$$P_s = \ left (\ frac {A_mA_c} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8}$$

Средняя мощность шума в полосе пропускания сообщения

$$Р- {} пс = WN_0$$

Подставим эти значения в формулу SNR канала .

$$\ left (SNR \ right) _ {C, SSBSC} = \ frac {Средний \: \: Мощность \: \: of \: \: SSBSC \: \: модулированный \: \: wave} {Средний \: \: Power \: \: of \: \: noise \: \: in \: \: message \: \: bandwidth}$$

$$\ Rightarrow \ left (SNR \ right) _ {C, SSBSC} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0}$$

Предположим, что полосовой шум смешан с модулированной волной SSBSC в канале, как показано на рисунке выше. Эта комбинация применяется в качестве одного из входных данных для модулятора продукта. Следовательно, вход этого продукта модулятора

$$v_1 \ left (t \ right) = s \ left (t \ right) + n \ left (t \ right)$$

$$v_1 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] + n_I \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right)$$

Локальный генератор генерирует сигнал несущей $c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right)$. Этот сигнал подается как еще один вход для модулятора продукта. Таким образом, модулятор продукта производит вывод, который является произведением $v_1 \ left (t \ right)$ и $c \ left (t \ right)$.

$$v_2 \ left (t \ right) = v_1 \ left (t \ right) c \ left (t \ right)$$

Подставьте значения $v_1 \ left (t \ right)$ и $c \ left (t \ right)$ в вышеприведенном уравнении.

$\ Rightarrow v_2 (t) = (\ frac {A_mA_c} {2} \ cos [2 \ pi (f_c-f_m) t] + n_I (t) \ cos (2 \ pi f_ct) -$

$n_Q (t) \ sin (2 \ pi f_ct)) \ cos (2 \ pi f_ct)$

$\ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ право) +$

$n_I \ left (t \ right) \ cos ^ 2 \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct \ right)$

$\ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c-f_m \ right) t \ right] + \ cos \ left (2 \ pi f_mt \ right) \ right \} +$

$n_I \ left (t \ right) \ left (\ frac {1+ \ cos \ left (4 \ pi f_ct \ right)} {2} \ right) - n_Q \ left (t \ right) \ frac {\ sin \ left (4 \ pi f_ct \ right)} {2}$

Когда вышеуказанный сигнал применяется в качестве входа для фильтра нижних частот, мы получим выход фильтра нижних частот как

$$d \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left (2 \ pi f_mt \ right) + \ frac {n_I \ left (t \ right)} {2}$$

Средняя мощность демодулированного сигнала

$$P_m = \ left (\ frac {A_mA_c} {4 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32}$$

Средняя мощность шума на выходе

$$Р- {нет} = \ {гидроразрыва WN_0} {4}$$

Подставим эти значения в выходную формулу SNR

$$\ left (SNR \ right) _ {O, SSBSC} = \ frac {Среднее \: \: Мощность \: \: of \: \: демодулировано \: \: signal} {Среднее \: \: Мощность \: \: of \: \: noise \: \: at \: \: output}$$

$$\ Rightarrow \ left (SNR \ right) _ {O, SSBSC} = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} \ right ) / \ left (\ frac {WN_0} {4} \ right) = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0}$$

Замените значения на рисунке достоинства формулы приемника SSBSC

$$F = \ frac {\ left (SNR \ right) _ {O, SSBSC}} {\ left (SNR \ right) _ {C, SSBSC}}$$

$$F = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ right) / \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ right)$$

$$F = 1$$

Следовательно, показатель качества приемника SSBSC равен 1.