Что нам нужно в РНН?
Структура искусственной нейронной сети относительно проста и главным образом связана с умножением матрицы. На первом этапе входные данные умножаются на первоначально случайные веса, а смещение преобразуется с помощью функции активации, а выходные значения используются для прогнозирования. Этот шаг дает представление о том, как далеко сеть от реальности.
Применяемая метрика — это потеря. Чем выше функция потерь, тем тупее модель. Для улучшения знаний о сети требуется некоторая оптимизация путем корректировки весов сети. Стохастический градиентный спуск — это метод, используемый для изменения значений весов в направлении прав. После настройки сеть может использовать другую порцию данных для проверки своих новых знаний.
Ошибка, к счастью, ниже, чем раньше, но недостаточно мала. Этап оптимизации выполняется итеративно до тех пор, пока ошибка не будет минимизирована, т. Е. Больше информации не может быть извлечено.
Проблема с этим типом модели заключается в том, что у нее нет памяти. Это означает, что вход и выход независимы. Другими словами, модель не заботится о том, что было раньше. Возникает вопрос, когда вам нужно предсказать временные ряды или предложения, потому что сеть должна иметь информацию об исторических данных или прошлых словах.
Чтобы преодолеть эту проблему, был разработан новый тип архитектуры: Рекуррентная нейронная сеть (далее — RNN)
В этом уроке вы узнаете.
- Что нам нужно в РНН?
- Что такое RNN?
- Приложения РНН
- Ограничения РНН
- Улучшение LSTM
- РНН во временных рядах
- Создайте RNN для прогнозирования временных рядов в TensorFlow
Что такое RNN?
Рекуррентная нейронная сеть выглядит очень похоже на традиционную нейронную сеть за исключением того, что к нейронам добавляется состояние памяти. Вычисление для включения памяти просто.
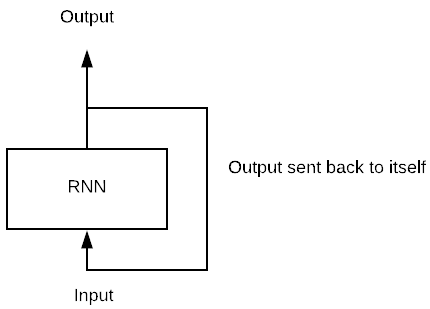
Представьте себе простую модель с одним потоком нейронов в пакете данных. В традиционной нейронной сети модель производит результат путем умножения входных данных на вес и функцию активации. При использовании RNN этот вывод отправляется обратно самому себе количество раз. Мы называем timestep количество времени, в течение которого выход становится входом следующего умножения матрицы.
Например, на рисунке ниже вы можете видеть, что сеть состоит из одного нейрона. Сеть вычисляет умножение матриц между входом и весом и добавляет нелинейность с функцией активации. Это становится выходом в t-1. Этот вывод является входом умножения второй матрицы.
Ниже мы кодируем простой RNN в тензорном потоке, чтобы понять шаг и форму вывода.
Сеть состоит из:
- Четыре входа
- Шесть нейронов
- 2-х тактные шаги
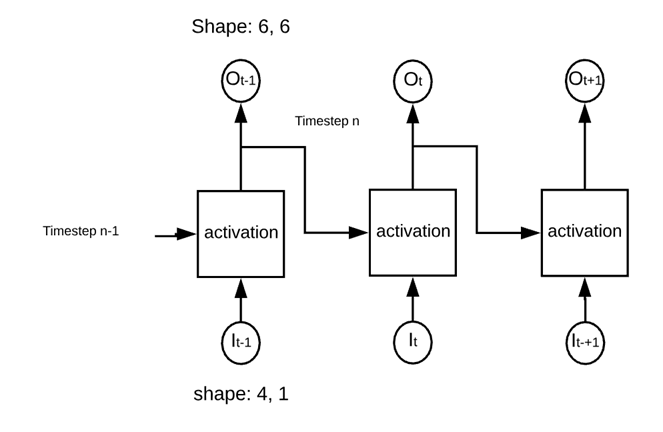
Сеть будет работать, как показано на рисунке ниже.
Сеть называется «периодической», поскольку она выполняет одну и ту же операцию в каждом квадрате активации. Сеть вычислила веса входов и предыдущего выхода, прежде чем использовать функцию активации.
import numpy as np
import tensorflow as tf
n_inputs = 4
n_neurons = 6
n_timesteps = 2
The data is a sequence of a number from 0 to 9 and divided into three batches of data.
## Data
X_batch = np.array([
[[0, 1, 2, 5], [9, 8, 7, 4]], # Batch 1
[[3, 4, 5, 2], [0, 0, 0, 0]], # Batch 2
[[6, 7, 8, 5], [6, 5, 4, 2]], # Batch 3
])
Мы можем построить сеть с заполнителем для данных, текущей стадии и выходных данных.
- Определите заполнитель для данных
X = tf.placeholder(tf.float32, [None, n_timesteps, n_inputs])
Вот:
- Нет: неизвестно и примет размер партии
- n_timesteps: сколько раз сеть отправит выходные данные обратно в нейрон
- n_inputs: количество входов на пакет
- Определить рекуррентную сеть
Как упомянуто на картинке выше, сеть состоит из 6 нейронов. Сеть будет вычислять два точечных произведения:
- Входные данные с первым набором весов (т.е. 6: равно числу нейронов)
- Предыдущий вывод со вторым набором весов (т.е. 6: соответствует номеру вывода)
Обратите внимание, что во время первой прямой связи значения предыдущего вывода равны нулю, потому что у нас нет доступных значений.
Объект для построения RNN — это tf.contrib.rnn.BasicRNNCell с аргументом num_units для определения количества входных данных.
basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
Теперь, когда сеть определена, вы можете вычислить выходы и состояния
outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32)
Этот объект использует внутренний цикл для умножения матриц соответствующее количество раз.
Обратите внимание, что рекурентный нейрон является функцией всех входов предыдущих временных шагов. Так сеть строит свою собственную память. Информация из предыдущего времени может распространяться в будущем. Это магия рекуррентной нейронной сети
## Define the shape of the tensor
X = tf.placeholder(tf.float32, [None, n_timesteps, n_inputs])
## Define the network
basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32)
init = tf.global_variables_initializer()
init = tf.global_variables_initializer()
with tf.Session() as sess:
init.run()
outputs_val = outputs.eval(feed_dict={X: X_batch})
print(states.eval(feed_dict={X: X_batch}))
[[ 0.38941205 -0.9980438 0.99750966 0.7892596 0.9978241 0.9999997 ]
[ 0.61096436 0.7255889 0.82977575 -0.88226104 0.29261455 -0.15597084]
[ 0.62091285 -0.87023467 0.99729395 -0.58261937 0.9811445 0.99969864]]
Для пояснения вы печатаете значения предыдущего состояния. Вывод, напечатанный выше, показывает вывод из последнего состояния. Теперь напечатайте все выходные данные, вы можете заметить, что состояния — это предыдущий вывод каждого пакета. То есть предыдущий вывод содержит информацию обо всей последовательности.
print(outputs_val)
print(outputs_val.shape)
[[[-0.75934666 -0.99537754 0.9735819 -0.9722234 -0.14234993
-0.9984044 ]
[ 0.99975264 -0.9983206 0.9999993 -1. -0.9997506
-1. ]]
[[ 0.97486496 -0.98773265 0.9969686 -0.99950117 -0.7092863
-0.99998885]
[ 0.9326837 0.2673438 0.2808514 -0.7535883 -0.43337247
0.5700631 ]]
[[ 0.99628735 -0.9998728 0.99999213 -0.99999976 -0.9884324
-1. ]
[ 0.99962527 -0.9467421 0.9997403 -0.99999714 -0.99929446
-0.9999795 ]]]
(3, 2, 6)
Выход имеет вид (3, 2, 6):
- 3: количество партий
- 2: номер временного шага
- 6: количество нейронов
Оптимизация рекуррентной нейронной сети идентична традиционной нейронной сети. Более подробно о том, как оптимизировать код, вы увидите в следующей части этого руководства.
Приложения РНН
RNN имеет многократное использование, особенно когда речь идет о прогнозировании будущего. В финансовой индустрии RNN может помочь в прогнозировании цен на акции или признака направления фондового рынка (т. Е. Положительного или отрицательного).
RNN полезен для автономного автомобиля, поскольку он может избежать автомобильной аварии, предвидя траекторию движения автомобиля.
RNN is widely used in text analysis, image captioning, sentiment analysis and machine translation. For example, one can use a movie review to understand the feeling the spectator perceived after watching the movie. Automating this task is very useful when the movie company does not have enough time to review, label, consolidate and analyze the reviews. The machine can do the job with a higher level of accuracy.
Limitations of RNN
In theory, RNN is supposed to carry the information up to time . However, it is quite challenging to propagate all this information when the time step is too long. When a network has too many deep layers, it becomes untrainable. This problem is called: vanishing gradient problem. If you remember, the neural network updates the weight using the gradient descent algorithm. The gradients grow smaller when the network progress down to lower layers.
In conclusion, the gradients stay constant meaning there is no space for improvement. The model learns from a change in the gradient; this change affects the network’s output. However, if the difference in the gradient is too small (i.e., the weights change a little), the network can’t learn anything and so the output. Therefore, a network facing a vanishing gradient problem cannot converge toward a good solution.
Improvement LSTM
To overcome the potential issue of vanishing gradient faced by RNN, three researchers, Hochreiter, Schmidhuber and Bengio improved the RNN with an architecture called Long Short-Term Memory (LSTM). In brief, LSMT provides to the network relevant past information to more recent time. The machine uses a better architecture to select and carry information back to later time.
LSTM architecture is available in TensorFlow, tf.contrib.rnn.LSTMCell. LSTM is out of the scope of the tutorial. You can refer to the official documentation for further information
RNN in time series
In this tutorial, you will use an RNN with time series data. Time series are dependent to previous time which means past values includes relevant information that the network can learn from. The idea behind time series prediction is to estimate the future value of a series, let’s say, stock price, temperature, GDP and so on.
The data preparation for RNN and time series can be a little bit tricky. First of all, the objective is to predict the next value of the series, meaning, you will use the past information to estimate the value at t + 1. The label is equal to the input sequence and shifted one period ahead. Secondly, the number of input is set to 1, i.e., one observation per time. Lastly, the time step is equal to the sequence of the numerical value. For instance, if you set the time step to 10, the input sequence will return ten consecutive times.
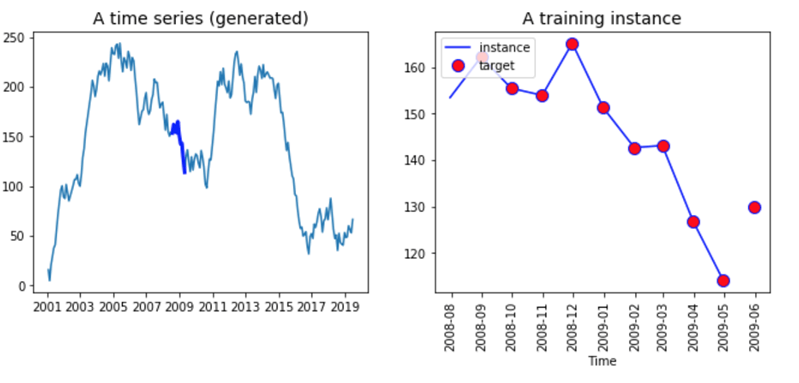
Look at the graph below, we have represented the time series data on the left and a fictive input sequence on the right. You create a function to return a dataset with random value for each day from January 2001 to December 2016
# To plot pretty figures
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
def create_ts(start = '2001', n = 201, freq = 'M'):
rng = pd.date_range(start=start, periods=n, freq=freq)
ts = pd.Series(np.random.uniform(-18, 18, size=len(rng)), rng).cumsum()
return ts
ts= create_ts(start = '2001', n = 192, freq = 'M')
ts.tail(5)
Вывод
2016-08-31 -93.459631 2016-09-30 -95.264791 2016-10-31 -95.551935 2016-11-30 -105.879611 2016-12-31 -123.729319 Freq: M, dtype: float64
ts = create_ts(start = '2001', n = 222)
# Left
plt.figure(figsize=(11,4))
plt.subplot(121)
plt.plot(ts.index, ts)
plt.plot(ts.index[90:100], ts[90:100], "b-", linewidth=3, label="A training instance")
plt.title("A time series (generated)", fontsize=14)
# Right
plt.subplot(122)
plt.title("A training instance", fontsize=14)
plt.plot(ts.index[90:100], ts[90:100], "b-", markersize=8, label="instance")
plt.plot(ts.index[91:101], ts[91:101], "bo", markersize=10, label="target", markerfacecolor='red')
plt.legend(loc="upper left")
plt.xlabel("Time")
plt.show()
Правая часть графика показывает все серии. Он начинается с 2001 года и заканчивается в 2019 году. Нет смысла подавать все данные в сети, вместо этого вам нужно создать пакет данных с длиной, равной временному шагу. Эта партия будет переменной X Переменная Y такая же, как X, но смещена на один период (т. Е. Вы хотите прогнозировать t + 1).
Оба вектора имеют одинаковую длину. Вы можете увидеть это в правой части приведенного выше графика. Линия представляет десять значений ввода X, а красные точки — десять значений метки Y. Обратите внимание, что метка начинается на один период раньше X и заканчивается на один период позже.
Создайте RNN для прогнозирования временных рядов в TensorFlow
Теперь пришло время построить свой первый RNN, чтобы предсказать серию выше. Вам необходимо указать некоторые гиперпараметры (параметры модели, т. Е. Количество нейронов и т. Д.) Для модели:
- Количество входов: 1
- Шаг по времени (окна во временных рядах): 10
- Количество нейронов: 120
- Количество выходов: 1
Ваша сеть будет учиться из последовательности 10 дней и содержит 120 повторяющихся нейронов. Вы кормите модель одним вводом, т. Е. Одним днем. Не стесняйтесь изменять значения, чтобы увидеть, улучшилась ли модель.
Прежде чем строить модель, вам нужно разделить набор данных на набор поездов и набор тестов. Полный набор данных имеет 222 точки данных; вы будете использовать первые 201 балл для обучения модели и последние 21 балл для тестирования вашей модели.
После того, как вы определили поезд и набор тестов, вам нужно создать объект, содержащий партии. В этих пакетах у вас есть значения X и Y. Помните, что значения X отстают на один период. Поэтому вы используете первые 200 наблюдений, и шаг по времени равен 10. Объект X_batches должен содержать 20 пакетов размером 10 * 1. Форма y_batches имеет ту же форму, что и объект X_batches, но на один период впереди.
Шаг 1) Создай поезд и проверь
Прежде всего, вы конвертируете серию в массив numpy; затем вы определяете окна (т. е. количество времени, в течение которого сеть будет учиться), количество входов, выходов и размер набора поездов.
series = np.array(ts) n_windows = 20 n_input = 1 n_output = 1 size_train = 201
После этого вы просто разделяете массив на два набора данных.
## Split data train = series[:size_train] test = series[size_train:] print(train.shape, test.shape) (201,) (21,)
Шаг 2) Создайте функцию для возврата X_batches и y_batches
Чтобы сделать это проще, вы можете создать функцию, которая возвращает два разных массива, один для X_batches и один для y_batches.
Давайте напишем функцию для построения пакетов.
Обратите внимание, что пакеты X отстают на один период (мы берем значение t-1). Вывод функции должен иметь три измерения. Первые измерения равны количеству пакетов, вторые — размеру окон, а последние — количеству входных данных.
Самое сложное — правильно выбрать точки данных. Для точек данных X вы выбираете наблюдения от t = 1 до t = 200, в то время как для точки данных Y вы возвращаете наблюдения от t = 2 до 201. Как только у вас есть правильные точки данных, их легко изменить сериал.
Чтобы построить объект с пакетами, вам нужно разделить набор данных на десять пакетов равной длины (т. Е. 20). Вы можете использовать метод изменения формы и передать -1, чтобы серия была похожа на размер пакета. Значение 20 — это количество наблюдений на партию, а 1 — количество входных данных.
Вы должны сделать тот же шаг, но для метки.
Обратите внимание, что вам нужно сместить данные на количество времени, которое вы хотите прогнозировать. Например, если вы хотите предсказать одно время вперед, то вы сдвигаете ряд на 1. Если вы хотите прогнозировать два дня, то сдвиньте данные на 2.
x_data = train[:size_train-1]: Select all the training instance minus one day
X_batches = x_data.reshape(-1, windows, input): create the right shape for the batch e.g (10, 20, 1)
def create_batches(df, windows, input, output):
## Create X
x_data = train[:size_train-1] # Select the data
X_batches = x_data.reshape(-1, windows, input) # Reshape the data
## Create y
y_data = train[n_output:size_train]
y_batches = y_data.reshape(-1, windows, output)
return X_batches, y_batches
Теперь, когда функция определена, вы можете вызвать ее для создания пакетов.
X_batches, y_batches = create_batches(df = train,
windows = n_windows,
input = n_input,
output = n_output)
Вы можете распечатать форму, чтобы убедиться в правильности размеров.
print(X_batches.shape, y_batches.shape) (10, 20, 1) (10, 20, 1)
Вам нужно создать тестовый набор только с одной партией данных и 20 наблюдениями.
Обратите внимание, что вы прогнозируете дни за днями, это означает, что второе прогнозируемое значение будет основано на истинном значении первого дня (t + 1) тестового набора данных. На самом деле, истинное значение будет известно.
Если вы хотите прогнозировать t + 2 (т.е. на два дня вперед), вам нужно использовать прогнозируемое значение t + 1; если вы собираетесь прогнозировать t + 3 (на три дня вперед), вам нужно использовать прогнозные значения t + 1 и t + 2. Имеет смысл, что трудно точно предсказать t + n дней вперед.
X_test, y_test = create_batches(df = test, windows = 20,input = 1, output = 1) print(X_test.shape, y_test.shape) (10, 20, 1) (10, 20, 1)
Хорошо, ваш размер пакета готов, вы можете построить архитектуру RNN. Помните, у вас есть 120 повторяющихся нейронов.
Шаг 3) Постройте модель
Чтобы создать модель, вам нужно определить три части:
- Переменная с тензорами
- РНН
- Потеря и оптимизация
Шаг 3.1) Переменные
Вам необходимо указать переменные X и Y с соответствующей формой. Этот шаг тривиален. Тензор имеет ту же размерность, что и объекты X_batches и y_batches.
Например, тензор X является заполнителем (обратитесь к руководству Введение в Tensorflow, чтобы освежить свой взгляд на объявление переменных), имеет три измерения:
- Примечание: размер партии
- n_windows: длина окон. то есть, сколько раз модель смотрит назад
- n_input: номер входа
Результат:
tf.placeholder(tf.float32, [None, n_windows, n_input])
## 1. Construct the tensors X = tf.placeholder(tf.float32, [None, n_windows, n_input]) y = tf.placeholder(tf.float32, [None, n_windows, n_output])
Шаг 3.2) Создание RNN
Во второй части вам необходимо определить архитектуру сети. Как и прежде, вы используете объект BasicRNNCell и dynamic_rnn из оценки TensorFlow.
## 2. create the model basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=r_neuron, activation=tf.nn.relu) rnn_output, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32)
Следующая часть немного сложнее, но позволяет ускорить вычисления. Вам необходимо преобразовать вывод прогона в плотный слой, а затем снова преобразовать его, чтобы иметь то же измерение, что и вход.
stacked_rnn_output = tf.reshape(rnn_output, [-1, r_neuron]) stacked_outputs = tf.layers.dense(stacked_rnn_output, n_output) outputs = tf.reshape(stacked_outputs, [-1, n_windows, n_output])
Шаг 3.3) Создание потерь и оптимизация
Оптимизация модели зависит от задачи, которую вы выполняете. В предыдущем уроке по CNN ваша цель состояла в классификации изображений, в этом уроке цель немного другая. Вас просят сделать прогноз по непрерывной переменной, сравниваемой с классом.
Это различие важно, потому что оно изменит проблему оптимизации. Задача оптимизации для непрерывной переменной состоит в минимизации среднеквадратичной ошибки. Чтобы построить эти метрики в TF, вы можете использовать:
- tf.reduce_sum (tf.square (выходные данные — y))
Остальная часть кода такая же, как и раньше; Вы используете оптимизатор Adam, чтобы уменьшить потери (т. е. MSE):
- tf.train.AdamOptimizer (learning_rate = learning_rate)
- optimizer.minimize (убыток)
Вот и все, вы можете собрать все вместе, и ваша модель готова к тренировкам.
tf.reset_default_graph() r_neuron = 120 ## 1. Construct the tensors X = tf.placeholder(tf.float32, [None, n_windows, n_input]) y = tf.placeholder(tf.float32, [None, n_windows, n_output]) ## 2. create the model basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=r_neuron, activation=tf.nn.relu) rnn_output, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32) stacked_rnn_output = tf.reshape(rnn_output, [-1, r_neuron]) stacked_outputs = tf.layers.dense(stacked_rnn_output, n_output) outputs = tf.reshape(stacked_outputs, [-1, n_windows, n_output]) ## 3. Loss + optimization learning_rate = 0.001 loss = tf.reduce_sum(tf.square(outputs - y)) optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate) training_op = optimizer.minimize(loss) init = tf.global_variables_initializer()
Вы будете тренировать модель, используя 1500 эпох, и печатать потери каждые 150 итераций. После того, как модель обучена, вы оцениваете модель на тестовом наборе и создаете объект, содержащий прогнозы.
iteration = 1500
with tf.Session() as sess:
init.run()
for iters in range(iteration):
sess.run(training_op, feed_dict={X: X_batches, y: y_batches})
if iters % 150 == 0:
mse = loss.eval(feed_dict={X: X_batches, y: y_batches})
print(iters, "\tMSE:", mse)
y_pred = sess.run(outputs, feed_dict={X: X_test})
0 MSE: 502893.34
150 MSE: 13839.129
300 MSE: 3964.835
450 MSE: 2619.885
600 MSE: 2418.772
750 MSE: 2110.5923
900 MSE: 1887.9644
1050 MSE: 1747.1377
1200 MSE: 1556.3398
1350 MSE: 1384.6113
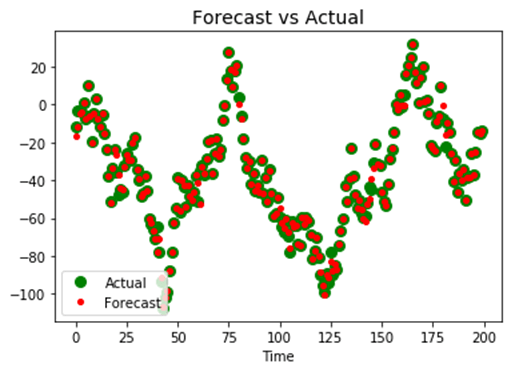
Наконец, вы можете построить фактическое значение ряда с прогнозируемым значением. Если ваша модель исправлена, предсказанные значения должны быть помещены поверх фактических значений.
Как видите, модель имеет место для улучшения. Это зависит от вас, чтобы изменить гиперпараметры, такие как окна, размер пакета числа повторяющихся нейронов.
plt.title("Forecast vs Actual", fontsize=14)
plt.plot(pd.Series(np.ravel(y_test)), "bo", markersize=8, label="Actual", color='green')
plt.plot(pd.Series(np.ravel(y_pred)), "r.", markersize=8, label="Forecast", color='red')
plt.legend(loc="lower left")
plt.xlabel("Time")
plt.show()
Резюме
Рекуррентная нейронная сеть — это надежная архитектура для анализа временных рядов или анализа текста. Результатом предыдущего состояния является обратная связь для сохранения памяти сети во времени или последовательности слов.
В TensorFlow вы можете использовать следующие коды для обучения текущей нейронной сети для временных рядов:
Параметры модели
n_windows = 20 n_input = 1 n_output = 1 size_train = 201
Определите модель
X = tf.placeholder(tf.float32, [None, n_windows, n_input]) y = tf.placeholder(tf.float32, [None, n_windows, n_output]) basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=r_neuron, activation=tf.nn.relu) rnn_output, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32) stacked_rnn_output = tf.reshape(rnn_output, [-1, r_neuron]) stacked_outputs = tf.layers.dense(stacked_rnn_output, n_output) outputs = tf.reshape(stacked_outputs, [-1, n_windows, n_output])
Построить оптимизацию
learning_rate = 0.001 loss = tf.reduce_sum(tf.square(outputs - y)) optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate) training_op = optimizer.minimize(loss)
Тренируй модель
init = tf.global_variables_initializer()
iteration = 1500
with tf.Session() as sess:
init.run()
for iters in range(iteration):
sess.run(training_op, feed_dict={X: X_batches, y: y_batches})
if iters % 150 == 0:
mse = loss.eval(feed_dict={X: X_batches, y: y_batches})
print(iters, "\tMSE:", mse)
y_pred = sess.run(outputs, feed_dict={X: X_test})