Мы имеем дело с изображениями во многих областях. Сейчас мы обрабатываем сигналы (изображения) в частотной области. Поскольку этот ряд Фурье и частотная область являются чисто математическими, поэтому мы постараемся свести к минимуму эту математическую часть и уделить больше внимания ее использованию в DIP.
Анализ частотной области
До сих пор все домены, в которых мы анализировали сигнал, анализируем его по времени. Но в частотной области мы анализируем сигнал не по времени, а по частоте.
Разница между пространственной областью и частотной областью
В пространственной области мы имеем дело с изображениями как есть. Значение пикселей изображения изменяется относительно сцены. В то время как в частотной области мы имеем дело со скоростью, с которой значения пикселей изменяются в пространственной области.
Давайте для простоты скажем так.
Пространственный домен
В простой пространственной области мы имеем дело непосредственно с матрицей изображения. Тогда как в частотной области мы имеем дело с изображением, подобным этому.
Частотная область
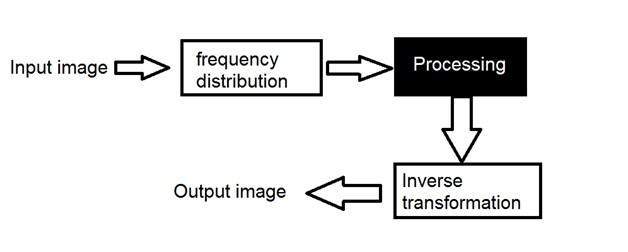
Сначала мы преобразуем изображение в его частотное распределение. Затем наша система «черного ящика» выполняет все необходимые операции, и в этом случае вывод черного ящика — это не изображение, а преобразование. После выполнения обратного преобразования оно преобразуется в изображение, которое затем просматривается в пространственной области.
Это можно наглядно рассматривать как
Здесь мы использовали слово трансформация. Что это на самом деле означает?
преобразование
Сигнал может быть преобразован из временной области в частотную область с использованием математических операторов, называемых преобразованиями. Есть много видов трансформации, которые делают это. Некоторые из них приведены ниже.
- Серия Фурье
- Преобразование Фурье
- Преобразование Лапласа
- Z преобразование
Из всего этого мы подробно обсудим ряды Фурье и преобразование Фурье в нашем следующем уроке.
Частотные составляющие
Любое изображение в пространственной области может быть представлено в частотной области. Но что на самом деле означают эти частоты?
Мы разделим частотные составляющие на два основных компонента.
Высокочастотные компоненты
Высокочастотные компоненты соответствуют краям изображения.
Низкочастотные компоненты
Низкочастотные составляющие в изображении соответствуют гладким областям.