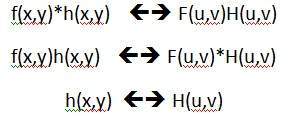В последнем уроке мы обсуждали изображения в частотной области. В этом уроке мы собираемся определить связь между частотной областью и изображениями (пространственная область).
Например
Рассмотрим этот пример.
То же изображение в частотной области может быть представлено как.
Теперь, какова связь между изображением или пространственной областью и частотной областью. Это соотношение может быть объяснено теоремой, которая называется теоремой свертки.
Теорема свертки
Связь между пространственной областью и частотной областью может быть установлена с помощью теоремы свертки.
Теорема свертки может быть представлена как.
Можно констатировать, что свертка в пространственной области равна фильтрации в частотной области и наоборот.
Фильтрация в частотной области может быть представлена следующим образом:
Шаги в фильтрации приведены ниже.
-
На первом этапе мы должны сделать некоторую предварительную обработку изображения в пространственной области, что означает увеличение его контрастности или яркости.
-
Тогда мы возьмем дискретное преобразование Фурье изображения
-
Затем мы будем центрировать дискретное преобразование Фурье, так как мы приведем дискретное преобразование Фурье в центр от углов
-
Затем мы применим фильтрацию, то есть умножим преобразование Фурье на функцию фильтра.
-
Тогда мы снова сместим ДПФ от центра к углам
-
Последний шаг — обратное дискретное преобразование Фурье, чтобы вернуть результат из частотной области в пространственную.
-
И этот шаг постобработки является необязательным, как и предварительная обработка, в которой мы просто увеличиваем внешний вид изображения.
На первом этапе мы должны сделать некоторую предварительную обработку изображения в пространственной области, что означает увеличение его контрастности или яркости.
Тогда мы возьмем дискретное преобразование Фурье изображения
Затем мы будем центрировать дискретное преобразование Фурье, так как мы приведем дискретное преобразование Фурье в центр от углов
Затем мы применим фильтрацию, то есть умножим преобразование Фурье на функцию фильтра.
Тогда мы снова сместим ДПФ от центра к углам
Последний шаг — обратное дискретное преобразование Фурье, чтобы вернуть результат из частотной области в пространственную.
И этот шаг постобработки является необязательным, как и предварительная обработка, в которой мы просто увеличиваем внешний вид изображения.
фильтры
Концепция фильтра в частотной области аналогична концепции маски в свертке.
После преобразования изображения в частотную область некоторые фильтры применяются в процессе фильтрации для выполнения различного рода обработки изображения. Обработка включает в себя размытие изображения, резкость изображения и т. Д.
Общий тип фильтров для этих целей:
- Идеальный фильтр верхних частот
- Идеальный фильтр низких частот
- Гауссовский фильтр верхних частот
- Гауссовский фильтр нижних частот
В следующем уроке мы подробно обсудим фильтр.