Мы обсудили некоторые из основных преобразований в нашем уроке Основы преобразования. В этом уроке мы рассмотрим некоторые основные преобразования уровня серого.
Улучшение изображения
Улучшение изображения обеспечивает лучшую контрастность и более детальное изображение по сравнению с не улучшенным изображением. Улучшение изображения имеет очень много применений. Он используется для улучшения медицинских изображений, изображений, полученных с помощью дистанционного зондирования, изображений со спутников и т. Д.
Функция преобразования была дана ниже
s = T (r)
где r — пиксели входного изображения, а s — пиксели выходного изображения. T является функцией преобразования, которая отображает каждое значение r на каждое значение s. Улучшение изображения может быть сделано с помощью преобразований уровня серого, которые обсуждаются ниже.
Преобразование уровня серого
Существует три основных преобразования уровня серого.
- линейный
- логарифмический
- Сила закона
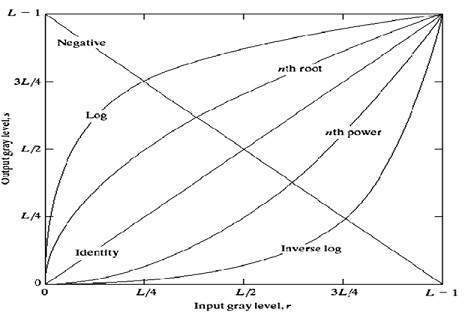
Общий график этих переходов показан ниже.
Линейное преобразование
Сначала мы рассмотрим линейное преобразование. Линейное преобразование включает в себя простую идентичность и отрицательное преобразование. Преобразование идентичности обсуждалось в нашем руководстве по преобразованию изображения, но здесь дано краткое описание этого преобразования.
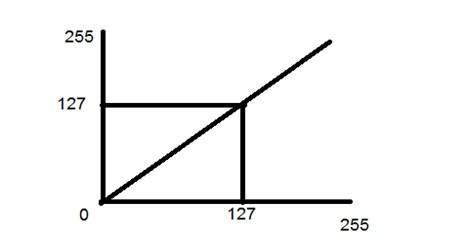
Переход идентичности показан прямой линией. При этом переходе каждое значение входного изображения напрямую отображается на каждое значение выходного изображения. Это приводит к тому же входному изображению и выходному изображению. И, следовательно, называется преобразованием личности. Это было показано ниже:
Негативное преобразование
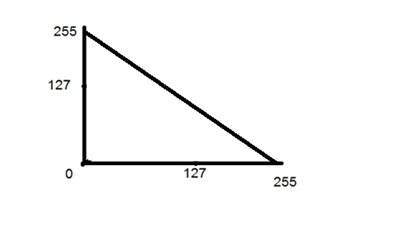
Второе линейное преобразование — это отрицательное преобразование, которое инвертирует преобразование идентичности. При отрицательном преобразовании каждое значение входного изображения вычитается из L-1 и отображается на выходное изображение.
Результат примерно такой.
Входное изображение
Выходное изображение
В этом случае был выполнен следующий переход.
s = (L — 1) — r
поскольку входное изображение Эйнштейна представляет собой изображение с 8 битами на пиксель, поэтому число уровней в этом изображении равно 256. Если положить 256 в уравнении, мы получим
с = 255 — г
Таким образом, каждое значение вычитается на 255, и результирующее изображение было показано выше. Так что получается, что более светлые пиксели становятся темными, а более темное изображение становится светлым. И это приводит к негативному изображению.
Это было показано на графике ниже.
Логарифмические преобразования
Логарифмическое преобразование дополнительно содержит два типа преобразования. Преобразование журнала и обратное преобразование журнала.
Преобразование журнала
Лог преобразования могут быть определены по этой формуле
s = c log (r + 1).
Где s и r — это значения пикселей на выходе и входном изображении, а c — это константа. Значение 1 добавляется к каждому значению пикселя входного изображения, потому что если в изображении присутствует интенсивность пикселей 0, тогда log (0) равен бесконечности. Таким образом, 1 добавляется, чтобы сделать минимальное значение как минимум 1.
Во время преобразования журнала темные пиксели в изображении расширяются по сравнению с более высокими значениями пикселей. Более высокие значения пикселей отчасти сжаты в преобразовании журнала. Это приводит к следующему улучшению изображения.
Значение c в преобразовании журнала корректирует вид улучшения, которое вы ищете.
Входное изображение
Log Tranform Image
Обратное лог-преобразование противоположно лог-преобразованию.
Власть — Закон преобразований
Есть еще две трансформации — степенные преобразования, которые включают n-ю степень и n-ную корневую трансформацию. Эти преобразования могут быть заданы выражением:
s = сг ^ γ
Этот символ γ называется гаммой, благодаря чему это преобразование также известно как гамма-преобразование.
Изменение значения γ влияет на улучшение изображений. Различные устройства отображения / мониторы имеют собственную гамма-коррекцию, поэтому они отображают свое изображение с различной интенсивностью.
Этот тип преобразования используется для улучшения изображений для различных типов устройств отображения. Гамма разных устройств отображения отличается. Например, гамма ЭЛТ лежит в диапазоне от 1,8 до 2,5, это означает, что изображение, отображаемое на ЭЛТ, темное.
Корректирующая гамма.
s = сг ^ γ
s = сг ^ (1 / 2.5)
Здесь показано то же изображение, но с разными значениями гаммы.
Например
Гамма = 10
Гамма = 8
Гамма = 6