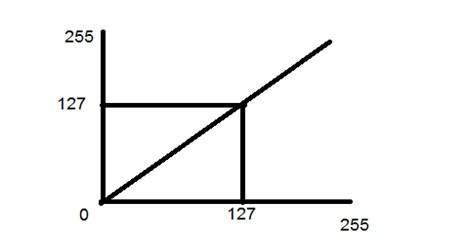
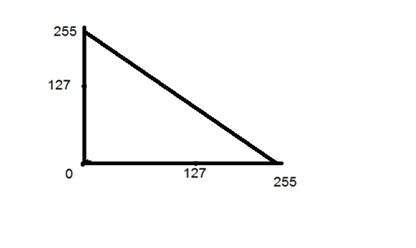
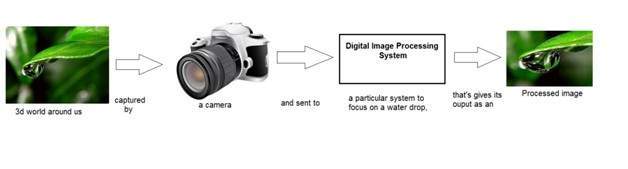
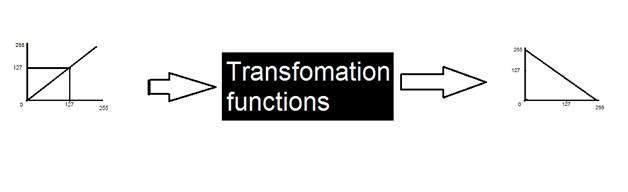
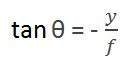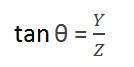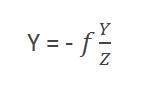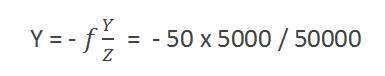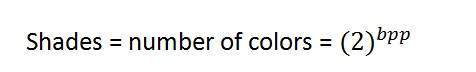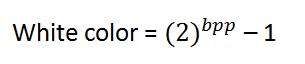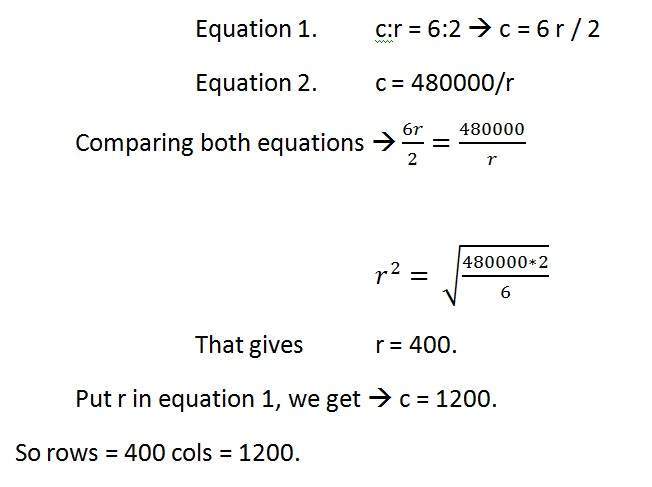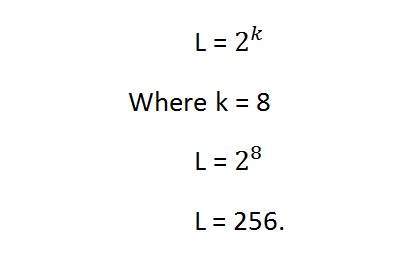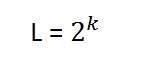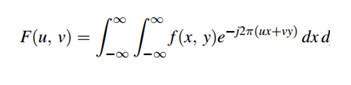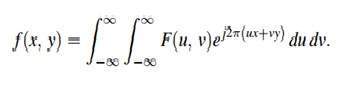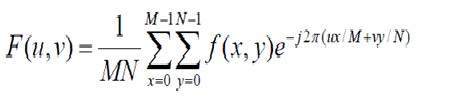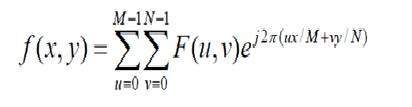Цифровая обработка изображений Введение

Обработка сигналов — это дисциплина в области электротехники и математики, которая занимается анализом и обработкой аналоговых и цифровых сигналов, а также хранением, фильтрацией и другими операциями с сигналами. Эти сигналы включают в себя сигналы передачи, звуковые или голосовые сигналы, сигналы изображения и другие сигналы и т. Д.

Из всех этих сигналов при обработке изображений выполняется поле, которое относится к типу сигналов, для которых вход является изображением, а вывод — также изображением. Как следует из названия, он занимается обработкой изображений.

Это может быть далее разделено на аналоговую обработку изображений и цифровую обработку изображений.

Аналоговая обработка изображений

Аналоговая обработка изображений производится на аналоговых сигналах. Включает обработку двухмерных аналоговых сигналов. В этом типе обработки изображения обрабатываются электрическими средствами путем изменения электрического сигнала. Общий пример включает телевизионное изображение.

Цифровая обработка изображений доминирует над аналоговой обработкой изображений с течением времени из-за более широкого спектра применений.

Цифровая обработка изображений

Обработка цифрового изображения связана с разработкой цифровой системы, которая выполняет операции с цифровым изображением.

Что такое изображение

Изображение — это не более чем двухмерный сигнал. Он определяется математической функцией f (x, y), где x и y — две координаты по горизонтали и вертикали.

Значение f (x, y) в любой точке дает значение пикселя в этой точке изображения.

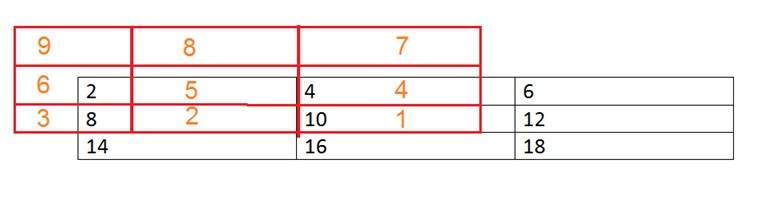
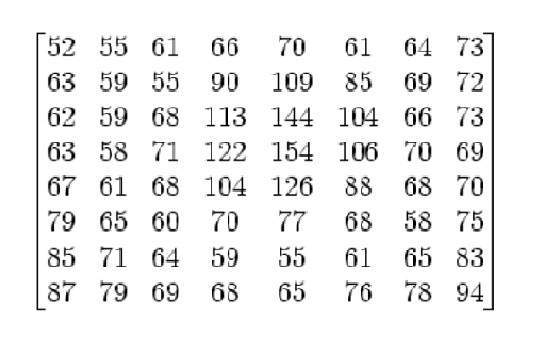
Приведенный выше рисунок является примером цифрового изображения, которое вы сейчас просматриваете на экране своего компьютера. Но на самом деле это изображение — не что иное, как двумерный массив чисел в диапазоне от 0 до 255.

128	30	123
232	123	321
123	77	89
80	255	255

Каждое число представляет значение функции f (x, y) в любой точке. В этом случае значения 128, 230, 123 каждый представляет отдельное значение пикселя. Размеры изображения на самом деле являются размерами этого двухмерного массива.

Связь между цифровым изображением и сигналом

Если изображение представляет собой двумерный массив, то какое оно имеет отношение к сигналу? Чтобы понять это, нам нужно сначала понять, что такое сигнал?

Сигнал

В физическом мире любая величина, измеряемая во времени в пространстве или в любом более высоком измерении, может восприниматься как сигнал. Сигнал является математической функцией и передает некоторую информацию. Сигнал может быть одномерным или двухмерным или более размерным сигналом. Одномерный сигнал — это сигнал, который измеряется во времени. Типичным примером является голосовой сигнал. Двумерные сигналы — это те, которые измеряются по некоторым другим физическим величинам. Примером двумерного сигнала является цифровое изображение. Мы рассмотрим более подробно в следующем уроке, как формируются и интерпретируются одномерные или двухмерные сигналы и более высокие сигналы.

отношения

Поскольку все, что передает информацию или передает сообщение в физическом мире между двумя наблюдателями, является сигналом. Это включает в себя речь или (человеческий голос) или изображение в качестве сигнала. Поскольку, когда мы говорим, наш голос преобразуется в звуковую волну / сигнал и преобразуется с учетом времени, с которым мы разговариваем. Не только это, но и способ работы цифровой камеры, так как при получении изображения с цифровой камеры требуется передача сигнала из одной части системы в другую.

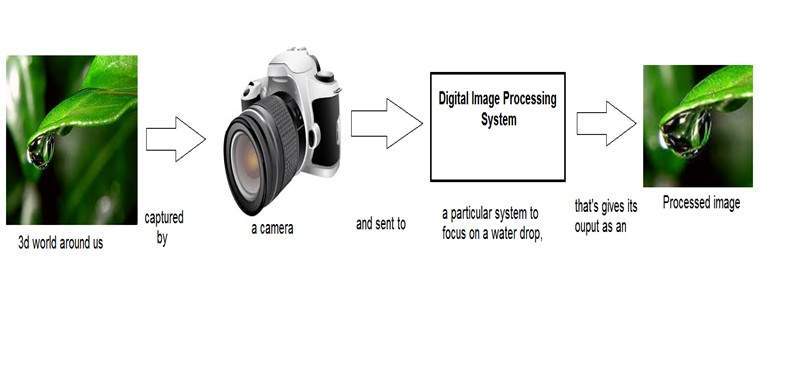
Как формируется цифровое изображение

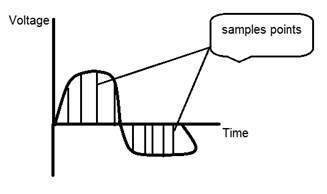
Поскольку захват изображения с камеры — это физический процесс. Солнечный свет используется в качестве источника энергии. Сенсорная матрица используется для получения изображения. Поэтому, когда солнечный свет падает на объект, количество света, отраженного этим объектом, воспринимается датчиками, и непрерывный сигнал напряжения генерируется количеством измеренных данных. Чтобы создать цифровое изображение, нам нужно преобразовать эти данные в цифровую форму. Это включает выборку и квантование. (Они обсуждаются позже). Результат выборки и квантования приводит к двумерному массиву или матрице чисел, которые являются ничем иным, как цифровым изображением.

Перекрывающиеся поля

Машинное / Компьютерное зрение

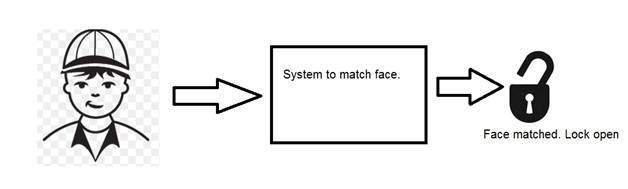
Машинное зрение или компьютерное зрение имеет дело с разработкой системы, в которой входными данными является изображение, а выходными данными является некоторая информация. Например: Разработка системы, которая сканирует человеческое лицо и открывает любой вид блокировки. Эта система будет выглядеть примерно так.

Компьютерная графика

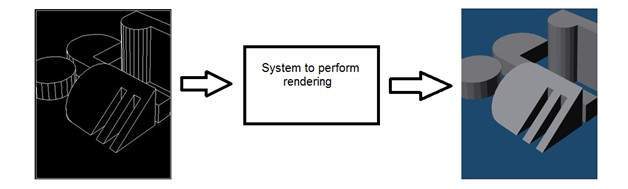
Компьютерная графика имеет дело с формированием изображений из объектных моделей, а не изображение захватывается каким-либо устройством. Например: рендеринг объектов. Генерация изображения из объектной модели. Такая система будет выглядеть примерно так.

Искусственный интеллект

Искусственный интеллект — это более или менее исследование внедрения человеческого интеллекта в машины. Искусственный интеллект имеет множество применений в обработке изображений. Например: разработка компьютерных систем диагностики, которые помогают врачам интерпретировать изображения рентгеновских лучей, МРТ и т. Д., А затем выделять заметные участки, которые должен осмотреть врач.

Обработка сигнала

Обработка сигналов является зонтиком, а обработка изображений лежит под ним. Количество света, отраженного объектом в физическом мире (трехмерном мире), проходит через объектив камеры, и оно становится двухмерным сигналом и, следовательно, приводит к формированию изображения. Затем это изображение оцифровывается с использованием методов обработки сигналов, а затем этим цифровым изображением манипулируют при цифровой обработке изображений.

Внедрение сигналов и систем

Этот учебник охватывает основы сигналов и системы, необходимые для понимания концепций цифровой обработки изображений. Прежде чем углубляться в концепции деталей, давайте сначала определим простые термины.

сигналы

В электротехнике фундаментальное количество представления некоторой информации называется сигналом. Неважно, что это за информация, то есть: аналоговая или цифровая информация. В математике сигнал — это функция, которая передает некоторую информацию. Фактически любая величина, измеряемая во времени в пространстве или любом более высоком измерении, может быть принята как сигнал. Сигнал может быть любого размера и любой формы.

Аналоговые сигналы

Сигнал может быть аналоговой величиной, что означает, что он определен относительно времени. Это непрерывный сигнал. Эти сигналы определены над непрерывными независимыми переменными. Их сложно анализировать, поскольку они несут огромное количество ценностей. Они очень точны из-за большой выборки значений. Для хранения этих сигналов вам требуется бесконечная память, поскольку она может достигать бесконечных значений в реальной строке. Аналоговые сигналы обозначаются синусоидальными волнами.

Например:

Человеческий голос

Человеческий голос является примером аналоговых сигналов. Когда вы говорите, производимый голос путешествует по воздуху в форме волн давления и, таким образом, принадлежит математической функции, имеющей независимые переменные пространства и времени и значение, соответствующее давлению воздуха.

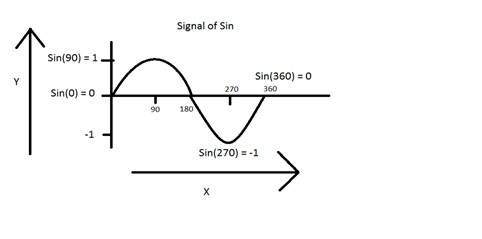
Другой пример — волна греха, которая показана на рисунке ниже.

Y = грех (х) где х не зависит

Цифровые сигналы

По сравнению с аналоговыми сигналами цифровые сигналы очень легко анализировать. Это прерывистые сигналы. Это присвоение аналоговых сигналов.

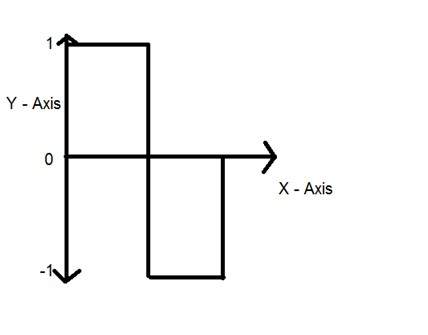
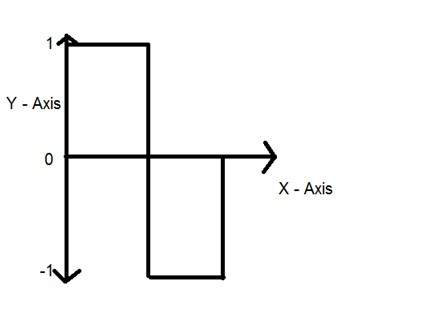
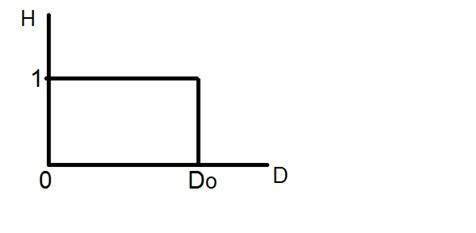
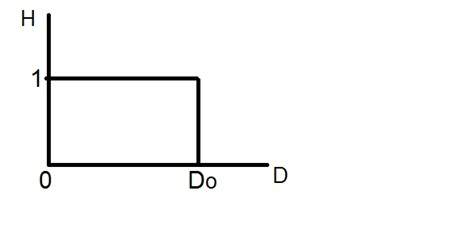
Слово digital обозначает дискретные значения и, следовательно, оно означает, что они используют конкретные значения для представления любой информации. В цифровом сигнале для представления чего-либо используются только два значения: 1 и 0 (двоичные значения). Цифровые сигналы менее точны, чем аналоговые, потому что они представляют собой дискретные выборки аналогового сигнала, взятые за некоторый период времени. Однако цифровые сигналы не подвержены шуму. Так что они длятся долго и их легко интерпретировать. Цифровые сигналы обозначаются прямоугольными волнами.

Например:

Компьютерная клавиатура

Всякий раз, когда клавиша нажимается на клавиатуре, соответствующий электрический сигнал отправляется на контроллер клавиатуры, содержащий значение ASCII этой конкретной клавиши. Например, электрический сигнал, который генерируется при нажатии клавиши клавиатуры a, несет информацию о цифре 97 в форме 0 и 1, которая является значением ASCII символа a.

Разница между аналоговыми и цифровыми сигналами

Элемент сравнения	Аналоговый сигнал	Цифровой сигнал
Анализ	Сложно	Можно анализировать
Представление	непрерывный	прерывистый
точность	Более точным	Менее точный
Место хранения	Бесконечная память	Легко хранится
С учетом шума	да	нет
Техника записи	Исходный сигнал сохраняется	Образцы сигнала взяты и сохранены
Примеры	Человеческий голос, термометр, аналоговые телефоны и т. Д.	Компьютеры, цифровые телефоны, цифровые ручки и т. Д.

системы

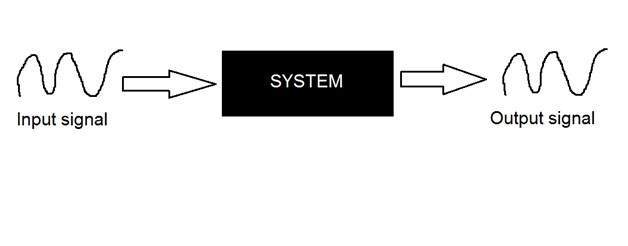
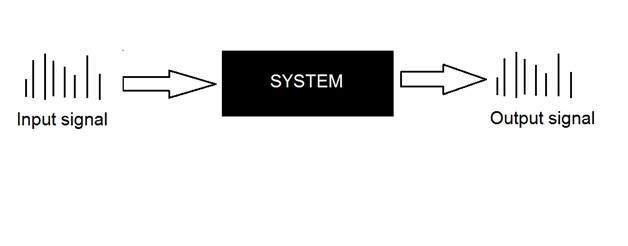
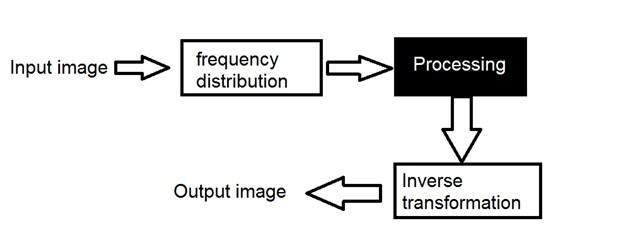
Система определяется типом ввода и вывода, с которым она имеет дело. Поскольку мы имеем дело с сигналами, то в нашем случае нашей системой будет математическая модель, фрагмент кода / программного обеспечения или физическое устройство, или черный ящик, вход которого является сигналом, и он выполняет некоторую обработку этого сигнала, и выходной сигнал. Вход известен как возбуждение, а выход известен как ответ.

На приведенном выше рисунке показана система, вход и выход которой являются сигналами, но вход является аналоговым сигналом. И на выходе это цифровой сигнал. Это означает, что наша система на самом деле является системой преобразования, которая преобразует аналоговые сигналы в цифровые сигналы.

Давайте посмотрим на внутреннюю часть этой системы черного ящика

Преобразование аналоговых в цифровые сигналы

Поскольку существует множество концепций, связанных с этим аналого-цифровым преобразованием и наоборот. Мы будем обсуждать только те, которые связаны с цифровой обработкой изображений. Есть две основные концепции, которые участвуют в покрытии.

• отбор проб

• квантование

отбор проб

квантование

отбор проб

Выборка, как следует из ее названия, может быть определена как отбор проб. Возьмите образцы цифрового сигнала по оси X. Выборка производится по независимой переменной. В случае этого математического уравнения:

Выборка производится по переменной x. Можно также сказать, что преобразование оси x (бесконечные значения) в цифровое выполняется при выборке.

Выборка далее делится на восходящую выборку и понижающую выборку. Если диапазон значений на оси х меньше, то мы увеличим выборку значений. Это называется повышающей выборкой, и наоборот, понижающей выборкой

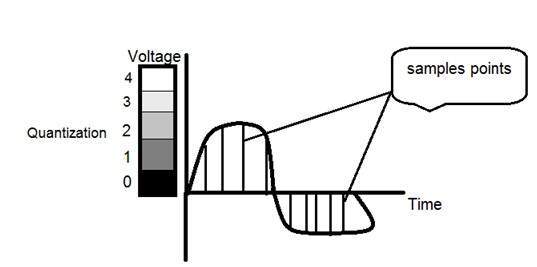
квантование

Квантование, как следует из его названия, может быть определено как деление на кванты (разделы). Квантование производится по зависимой переменной. Это противоположно выборке.

В случае этого математического уравнения y = sin (x)

Квантование выполняется по переменной Y. Это сделано на оси Y. Преобразование бесконечных значений оси y в 1, 0, -1 (или любой другой уровень) называется квантованием.

Это два основных этапа, которые используются при преобразовании аналогового сигнала в цифровой.

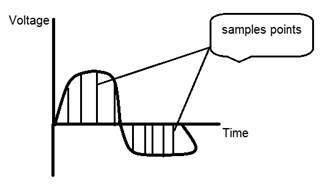
Квантование сигнала показано на рисунке ниже.

Зачем нам нужно преобразовывать аналоговый сигнал в цифровой сигнал.

Первая и очевидная причина заключается в том, что цифровая обработка изображений связана с цифровыми изображениями, которые являются цифровыми сигналами. Поэтому, когда изображение захватывается, оно конвертируется в цифровой формат и затем обрабатывается.

Вторая и важная причина заключается в том, что для выполнения операций с аналоговым сигналом на цифровом компьютере вы должны сохранить этот аналоговый сигнал в компьютере. А чтобы сохранить аналоговый сигнал, для его хранения требуется бесконечная память. И поскольку это невозможно, поэтому мы преобразуем этот сигнал в цифровой формат, а затем сохраняем его на цифровом компьютере и затем выполняем операции с ним.

Непрерывные системы против дискретных систем

Непрерывные системы

Тип систем, чьи вход и выход являются непрерывными или аналоговыми сигналами, называют непрерывными системами.

Дискретные системы

Тип систем, чьи вход и выход представляют собой дискретные сигналы или цифровые сигналы, называют цифровыми системами.

История фотографии

Происхождение камеры

История камеры и фотографии не совсем совпадает. Концепции камеры были введены намного раньше, чем концепция фотографии

Камера обскура

История камеры лежит в Азии. Принципы камеры были впервые представлены китайским философом MOZI. Это известно как камера-обскура. Камеры развивались по этому принципу.

Слово «камера-обскура» происходит от двух разных слов. Камера и обскура. Значение слова «камера» — это комната или какое-то хранилище, а «Обскура» означает «темнота».

Концепция, которая была введена китайским философом, состоит из устройства, которое проецирует изображение его окружения на стену. Однако он не был построен китайцами.

Создание камеры обскура

Концепция китайского языка была воплощена в жизнь мусульманским ученым Абу Али аль-Хасаном ибн аль-Хайтамом, широко известным как Ибн аль-Хайтам. Он построил первую камеру-обскура. Его камера следует принципам камеры-обскуры. Он построил это устройство где-то около 1000.

Портативная камера

В 1685 году Иоганн Зан построил первую портативную камеру. До появления этого устройства камеры состояли из комнаты размером и не были портативными. Хотя ирландским ученым Робертом Бойлом и Робертом Гуком было сделано устройство, которое было переносной камерой, но все же это устройство было очень большим, чтобы переносить его из одного места в другое.

Происхождение фотографии

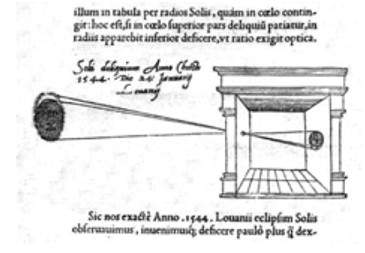
Хотя камера-обскура была построена в 1000 году мусульманским ученым. Но его первое фактическое использование было описано в 13-м веке английским философом Роджером Бэконом. Роджер предложил использовать камеру для наблюдения солнечных затмений.

Да Винчи

Хотя до 15-го века было сделано много улучшений, но улучшения и результаты, сделанные Леонардо ди Сер Пьеро да Винчи, были замечательными. Да Винчи был великим художником, музыкантом, анатомом и военным инженером. Ему приписывают многие изобретения. Его одна из самых известных картин включает в себя картину Моны Лизы.

Да Винчи не только построил камеру-обскуру, следуя принципу камеры с точечным отверстием, но и использует ее в качестве средства рисования для своих художественных работ. В его работе, которая была описана в Codex Atlanticus, были определены многие принципы камеры-обскуры.

Его камера работает по принципу камеры с точечным отверстием, которую можно описать как

Когда изображения освещенных объектов проникают через маленькое отверстие в очень темную комнату, вы увидите [на противоположной стене] эти объекты в правильной форме и цвете, уменьшенные в размерах в обратном положении из-за пересечения лучей.

Первая фотография

Первая фотография была сделана в 1814 году французским изобретателем Жозефом Никифором Ньепсом. Он снимает первую фотографию вида из окна в Ле-Гра, покрывая оловянную плиту битумом и после этого выставляя эту пластину на свет.

Первая подводная фотография

Первая подводная фотография была сделана английским математиком Уильямом Томсоном с использованием водонепроницаемой коробки. Это было сделано в 1856 году.

Происхождение фильма

Происхождение фильма было введено американским изобретателем и филантропом, известным как Джордж Истман, который считается пионером фотографии.

Он основал компанию Eastman Kodak, которая славится разработкой фильмов. Компания начинает производство бумажной пленки в 1885 году. Сначала он создал камеру Kodak, а затем и Brownie. Брауни был коробочной камерой и приобрел свою популярность благодаря функции Snapshot.

После появления фильма индустрия камер снова получила бум, и одно изобретение привело к другому.

Лейка и Аргус

Leica и argus — две аналоговые камеры, разработанные в 1925 и 1939 годах соответственно. Камера Leica была построена с использованием 35-мм кинопленки.

Аргус был другой аналоговой камерой, которая использует 35-миллиметровый формат и был довольно недорогим по сравнению с Leica и стал очень популярным.

Аналоговые камеры видеонаблюдения

В 1942 году немецкий инженер Вальтер Брух разработал и установил самую первую систему аналоговых камер видеонаблюдения. Ему также приписывают изобретение цветного телевидения в 1960 году.

Фото пак

Первая одноразовая камера была представлена ​​в 1949 году компанией Photo Pac. Эта камера использовалась только один раз, и в нее уже был включен рулон пленки. Более поздние версии Photo pac были водонепроницаемыми и даже имели вспышку.

Цифровые фотоаппараты

Mavica от Sony

Mavica (магнитная видеокамера) была запущена Sony в 1981 году и стала первым изменителем игр в мире цифровых камер. Изображения были записаны на дискеты, и изображения можно будет просмотреть позже на любом экране монитора.

Это была не просто цифровая камера, а аналоговая камера. Но получил свою популярность благодаря тому, что на нем хранились образы на дискетах. Это означает, что теперь вы можете хранить изображения в течение длительного периода, и вы можете сохранять огромное количество изображений на дискете, которые заменяются новыми чистыми дисками, когда они заполнятся. Mavica может хранить 25 изображений на диске.

Еще одна важная вещь, которую представила mavica, — это 0,3 мегапиксельная емкость для захвата фотографий.

Цифровые фотоаппараты

Камера Fuji DS-1P от Fuji films 1988 была первой настоящей цифровой камерой

Nikon D1 был 2,74-мегапиксельной камерой и первой коммерческой цифровой зеркальной камерой, разработанной Nikon, и была очень доступной для профессионалов.

Сегодня цифровые камеры включены в мобильные телефоны с очень высоким разрешением и качеством.

Приложения и использование

Поскольку цифровая обработка изображений имеет очень широкие области применения и DIP влияет почти на все технические области, мы просто обсудим некоторые из основных областей применения DIP.

Цифровая обработка изображений не ограничивается только настройкой пространственного разрешения повседневных изображений, снятых камерой. Это не ограничивается только увеличением яркости фотографии и т. Д. Скорее, это гораздо больше, чем это.

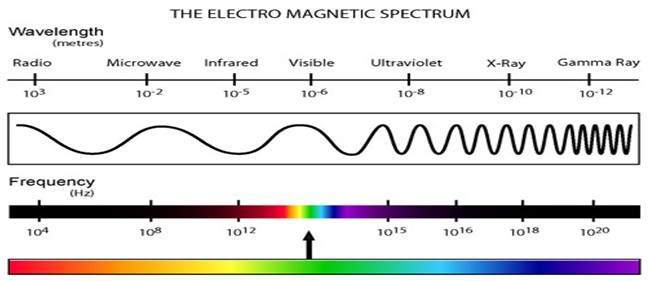
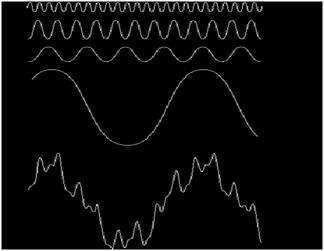
Электромагнитные волны можно рассматривать как поток частиц, где каждая частица движется со скоростью света. Каждая частица содержит пучок энергии. Этот пучок энергии называется фотоном.

Электромагнитный спектр в соответствии с энергией фотона показан ниже.

В этом электромагнитном спектре мы можем видеть только видимый спектр. Видимый спектр в основном включает в себя семь различных цветов, которые обычно называют как (VIBGOYR). VIBGOYR означает фиолетовый, индиго, синий, зеленый, оранжевый, желтый и красный.

Но это не отменяет существование других вещей в спектре. Наш человеческий глаз может видеть только видимую часть, в которой мы видели все объекты. Но камера может видеть другие вещи, которые невооруженным глазом не может видеть. Например: рентгеновские лучи, гамма-лучи и т. Д. Следовательно, анализ всего этого тоже делается в цифровой обработке изображений.

Это обсуждение приводит к другому вопросу, который

почему мы должны анализировать все эти другие вещи в спектре EM тоже?

Ответ на этот вопрос заключается в том, что этот другой материал, такой как XRay, широко используется в области медицины. Анализ гамма-излучения необходим, потому что он широко используется в ядерной медицине и астрономических наблюдениях. То же самое относится и к остальным вещам в спектре ЭМ.

Приложения цифровой обработки изображений

Ниже перечислены некоторые из основных областей, в которых широко используется цифровая обработка изображений.

• Заточка и восстановление изображений

• Медицинская сфера

• Дистанционное зондирование

• Передача и кодирование

• Машинное / Роботное зрение

• Обработка цвета

• Распознавание образов

• Обработка видео

• Микроскопическая визуализация

• другие

Заточка и восстановление изображений

Медицинская сфера

Дистанционное зондирование

Передача и кодирование

Машинное / Роботное зрение

Обработка цвета

Распознавание образов

Обработка видео

Микроскопическая визуализация

другие

Заточка и восстановление изображений

Заточка и восстановление изображений относится здесь к обработке изображений, которые были получены с современной камеры, чтобы сделать их более качественными или манипулировать этими изображениями для достижения желаемого результата. Это относится к тому, что обычно делает Photoshop.

Это включает в себя масштабирование, размытие, повышение резкости, преобразование оттенков серого в цвет, обнаружение краев и наоборот, поиск изображений и распознавание изображений. Типичные примеры:

Исходное изображение

Увеличенное изображение

Размытие изображения

Резкое изображение

Ребра

Медицинская сфера

Общие применения DIP в области медицины

1. Гамма лучи

2. Сканирование ПЭТ

3. Рентгеновский снимок

4. Медицинская КТ

5. УФ-изображения

Гамма лучи

Сканирование ПЭТ

Рентгеновский снимок

Медицинская КТ

УФ-изображения

УФ-изображения

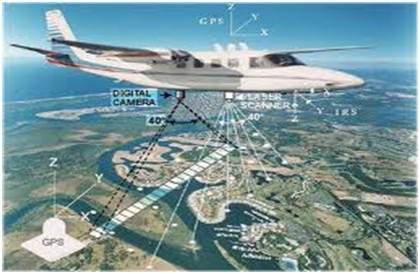
В области дистанционного зондирования область земли сканируется спутником или с очень высокой высоты, а затем анализируется для получения информации о ней. Одним конкретным применением цифровой обработки изображений в области дистанционного зондирования является обнаружение повреждений инфраструктуры, вызванных землетрясением.

Так как на улов уходит больше времени, даже если серьезный ущерб сфокусирован на. Поскольку площадь, вызванная землетрясением, иногда настолько велика, что невозможно оценить ее человеческим глазом, чтобы оценить ущерб. Даже если это так, то это очень беспокойная и длительная процедура. Таким образом, решение этого находится в цифровой обработке изображений. Изображение пострадавшего района снимается с надземной поверхности, а затем анализируется для обнаружения различных типов повреждений, нанесенных землетрясением.

Ключевые этапы, включенные в анализ:

1. Извлечение краев

2. Анализ и улучшение различных типов ребер

Извлечение краев

Анализ и улучшение различных типов ребер

Передача и кодирование

Самое первое изображение, которое было передано по проводам, было из Лондона в Нью-Йорк по подводному кабелю. Картинка, которая была отправлена, показана ниже.

Отправленная фотография заняла три часа, чтобы добраться из одного места в другое.

А теперь представьте, что сегодня мы можем просматривать прямые трансляции или прямые видеотрансляции с одного континента на другой с задержкой в ​​несколько секунд. Это означает, что в этой области также проделана большая работа. Это поле фокусируется не только на передаче, но и на кодировании. Многие различные форматы были разработаны для высокой или низкой полосы пропускания, чтобы кодировать фотографии и затем передавать их через Интернет или т. Д.

Машинное / Роботное зрение

Помимо множества проблем, с которыми сегодня сталкивается робот, одной из самых больших задач по-прежнему является улучшение видения робота. Сделайте так, чтобы робот мог видеть вещи, идентифицировать их, определять препятствия и т. Д. В этой области была проделана большая работа, и для работы над ней было введено совершенно другое поле компьютерного зрения.

Обнаружение препятствий

Обнаружение препятствий является одной из распространенных задач, выполняемых посредством обработки изображений, путем идентификации объектов различного типа на изображении и последующего вычисления расстояния между роботом и препятствиями.

Линейный робот

Большинство роботов сегодня следуют за линией и поэтому называются роботами следования за линией. Это поможет роботу двигаться по своему пути и выполнять некоторые задачи. Это также было достигнуто с помощью обработки изображений.

Обработка цвета

Обработка цвета включает обработку цветных изображений и различных цветовых пространств, которые используются. Например, цветовая модель RGB, YCbCr, HSV. Это также включает изучение передачи, хранения и кодирования этих цветных изображений.

Распознавание образов

Распознавание образов включает в себя изучение изображений и других областей, включая машинное обучение (раздел искусственного интеллекта). При распознавании образов обработка изображений используется для идентификации объектов на изображениях, а затем машинное обучение используется для обучения системы изменениям рисунка. Распознавание образов используется в компьютерной диагностике, распознавании почерка, распознавании изображений и т. Д.

Обработка видео

Видео — это не что иное, как очень быстрое перемещение картинок. Качество видео зависит от количества кадров / изображений в минуту и ​​качества каждого используемого кадра. Обработка видео включает в себя уменьшение шума, улучшение детализации, обнаружение движения, преобразование частоты кадров, преобразование формата изображения, преобразование цветового пространства и т. Д.

Концепция размеров

Мы рассмотрим этот пример, чтобы понять концепцию измерения.

Представьте, что у вас есть друг, который живет на Луне, и он хочет отправить вам подарок на ваш подарок на день рождения. Он спрашивает вас о вашем пребывании на земле. Единственная проблема заключается в том, что курьерская служба на Луне не понимает алфавитный адрес, а понимает только числовые координаты. Так как вы отправите ему свою позицию на земле?

Вот откуда приходит понятие размеров. Размеры определяют минимальное количество точек, необходимое для указания позиции любого конкретного объекта в пространстве.

Итак, давайте снова вернемся к нашему примеру, в котором вы должны отправить свою позицию на земле своему другу на Луне. Вы посылаете ему три пары координат. Первый называется долготой, второй — широтой, а третий — высотой.

Эти три координаты определяют ваше положение на земле. Первые два определяют ваше местоположение, а третий определяет вашу высоту над уровнем моря.

Таким образом, это означает, что для определения вашей позиции на земле требуются только три координаты. Это означает, что вы живете в мире, который является трехмерным. И, таким образом, это не только отвечает на вопрос об измерении, но также отвечает на причину, по которой мы живем в трехмерном мире.

Поскольку мы изучаем эту концепцию применительно к цифровой обработке изображений, теперь мы собираемся связать эту концепцию измерения с изображением.

Размеры изображения

Итак, если мы живем в трехмерном мире, то есть в трехмерном мире, то каковы размеры изображения, которое мы снимаем? Изображение является двухмерным, поэтому мы также определяем изображение как двухмерный сигнал. Изображение имеет только высоту и ширину. Изображение не имеет глубины. Просто посмотрите на это изображение ниже.

Если вы посмотрите на рисунок выше, он показывает, что у него есть только две оси, которые являются осью высоты и ширины. Вы не можете воспринимать глубину от этого изображения. Вот почему мы говорим, что изображение является двухмерным сигналом. Но наш глаз способен воспринимать трехмерные объекты, но это будет более подробно объяснено в следующем уроке о том, как работает камера и как воспринимается изображение.

Это обсуждение приводит к некоторым другим вопросам о том, как 3-мерные системы формируются из 2-мерного.

Как работает телевидение?

Если мы посмотрим на изображение выше, мы увидим, что это двухмерное изображение. Чтобы преобразовать его в три измерения, нам нужно еще одно измерение. Давайте возьмем время в качестве третьего измерения, в этом случае мы переместим это двухмерное изображение на время третьего измерения. То же самое понятие, которое происходит в телевидении, которое помогает нам воспринимать глубину различных объектов на экране. Означает ли это, что то, что появляется на телевизоре, или то, что мы видим на экране телевизора, — это 3d. Ну, мы можем да. Причина в том, что в случае телевидения мы, если мы играем видео. Тогда видео — это не что иное, как двухмерные картинки, движущиеся во временном измерении. Поскольку двумерные объекты движутся над третьим измерением, которое является временем, мы можем сказать, что оно трехмерное.

Разные размеры сигналов

1 размерный сигнал

Типичным примером одномерного сигнала является сигнал. Это может быть математически представлено как

F (x) = форма волны

Где х независимая переменная Поскольку это одномерный сигнал, поэтому используется только одна переменная x.

Наглядное представление одномерного сигнала приведено ниже:

На рисунке выше показан одномерный сигнал.

Теперь это приводит к другому вопросу, который, хотя это одномерный сигнал, тогда почему он имеет две оси? Ответ на этот вопрос заключается в том, что, хотя это одномерный сигнал, мы рисуем его в двухмерном пространстве. Или мы можем сказать, что пространство, в котором мы представляем этот сигнал, является двухмерным. Вот почему это выглядит как двухмерный сигнал.

Возможно, вы сможете лучше понять концепцию одного измерения, посмотрев на рисунок ниже.

Теперь вернемся к нашему первоначальному обсуждению измерения. Рассмотрим приведенную выше фигуру как реальную линию с положительными числами от одной точки к другой. Теперь, если нам нужно объяснить местоположение любой точки на этой линии, нам просто нужно только одно число, что означает только одно измерение.

2-х мерный сигнал

Типичным примером двумерного сигнала является изображение, которое уже обсуждалось выше.

Как мы уже видели, изображение является двухмерным сигналом, т.е. оно имеет два измерения. Это может быть математически представлено как:

F (x, y) = изображение

Где х и у две переменные. Концепция двух измерений также может быть объяснена в терминах математики как:

Теперь на рисунке выше обозначьте четыре угла квадрата как A, B, C и D соответственно. Если мы назовем один отрезок линии на рисунке AB, а другой CD, то мы увидим, что эти два параллельных отрезка соединяются и образуют квадрат. Каждый линейный сегмент соответствует одному измерению, поэтому эти два линейных сегмента соответствуют 2 измерениям.

3-х мерный сигнал

Трехмерный сигнал, как он называется, относится к тем сигналам, которые имеют три измерения. Самый распространенный пример был обсужден в начале, который касается нашего мира. Мы живем в трехмерном мире. Этот пример обсуждался очень детально. Другим примером трехмерного сигнала является куб или объемные данные, или наиболее распространенным примером может быть анимированный или трехмерный мультипликационный персонаж.

Математическое представление трехмерного сигнала:

F (x, y, z) = анимированный персонаж.

Другая ось или измерение Z вовлечено в трехмерное измерение, которое создает иллюзию глубины. В декартовой системе координат это можно рассматривать как:

4-х мерный сигнал

В четырехмерном сигнале участвуют четыре измерения. Первые три аналогичны трехмерному сигналу: (X, Y, Z), а четвертый, добавленный к ним, — это T (время). Время часто называют временным измерением, которое является способом измерения изменений. Математически сигнал 4 d можно записать как:

F (x, y, z, t) = анимационный фильм.

Типичным примером 4-мерного сигнала может быть анимированный 3D-фильм. Поскольку каждый персонаж является трехмерным персонажем, а затем они перемещаются относительно времени, из-за чего мы увидели иллюзию трехмерного фильма, больше похожего на реальный мир.

Таким образом, это означает, что на самом деле анимационные фильмы являются четырехмерными, то есть: перемещение трехмерных персонажей во времени четвертого измерения.

Формирование изображения на камеру

Как работает человеческий глаз?

Прежде чем мы обсудим формирование изображения на аналоговых и цифровых камерах, мы должны сначала обсудить формирование изображения на человеческом глазу. Поскольку основной принцип, которому следуют камеры, был взят с пути, человеческий глаз работает.

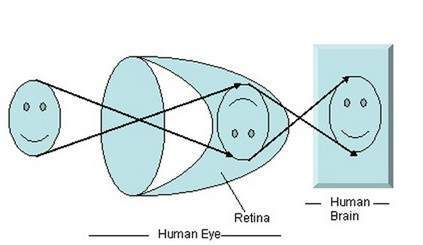
Когда свет падает на конкретный объект, он отражается обратно после удара сквозь объект. Лучи света при прохождении через хрусталик глаза образуют определенный угол, и изображение формируется на сетчатке, которая является задней стороной стенки. Образ, который сформирован, является инвертированным. Этот образ затем интерпретируется мозгом, и это позволяет нам понимать вещи. Благодаря формированию угла мы можем воспринимать высоту и глубину видимого объекта. Это было более объяснено в учебнике по перспективной трансформации.

Как видно из рисунка выше, когда солнечный свет падает на объект (в данном случае это лицо), он отражается назад, и разные лучи образуют разный угол при прохождении через линзу и инвертированное изображение объект был сформирован на задней стенке. Последняя часть рисунка обозначает, что объект был интерпретирован мозгом и перевернут.

Теперь давайте вернемся к формированию изображения на аналоговых и цифровых камерах.

Формирование изображения на аналоговых камерах

В аналоговых камерах формирование изображения происходит из-за химической реакции, которая происходит на полосе, которая используется для формирования изображения.

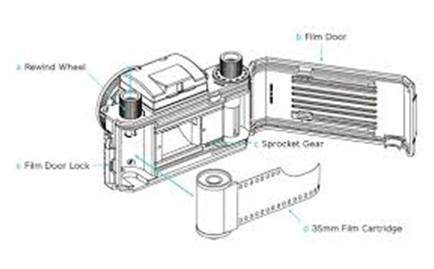
Полоса 35 мм используется в аналоговой камере. Обозначается на рисунке 35-мм пленочным картриджем. Эта полоса покрыта галогенидом серебра (химическое вещество).

Полоса 35 мм используется в аналоговой камере. Обозначается на рисунке 35-мм пленочным картриджем. Эта полоса покрыта галогенидом серебра (химическое вещество).

Свет — это не что иное, как мелкие частицы, известные как частицы фотонов. Поэтому, когда эти частицы фотонов проходят через камеру, он реагирует с частицами галогенида серебра на полосе и приводит к серебру, которое является негативом изображения.

Чтобы понять это лучше, взгляните на это уравнение.

Фотоны (легкие частицы) + галогенид серебра? Серебряный ? изображение негативное.

Это только основы, хотя формирование изображения включает в себя много других концепций, касающихся прохождения света внутри, а также концепции затвора и скорости затвора, диафрагмы и ее открытия, но сейчас мы перейдем к следующей части. Хотя большинство из этих концепций были обсуждены в нашем уроке о затворе и диафрагме.

Это только основы, хотя формирование изображения включает в себя много других концепций, касающихся прохождения света внутри, а также концепции затвора и скорости затвора, диафрагмы и ее открытия, но сейчас мы перейдем к следующей части. Хотя большинство из этих концепций были обсуждены в нашем уроке о затворе и диафрагме.

Формирование изображения на цифровых камерах

В цифровых камерах формирование изображения не происходит из-за химической реакции, а происходит немного сложнее, чем это. В цифровой камере матрица ПЗС датчиков используется для формирования изображения.

Формирование изображения через матрицу CCD

CCD обозначает устройство с зарядовой связью. Это датчик изображения, и, как и другие датчики, он измеряет значения и преобразует их в электрический сигнал. В случае ПЗС он воспринимает изображение и преобразует его в электрический сигнал и т. Д.

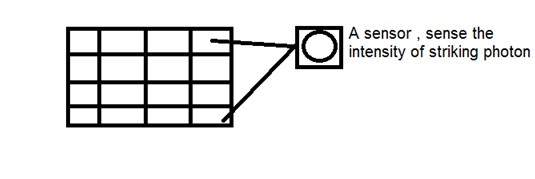
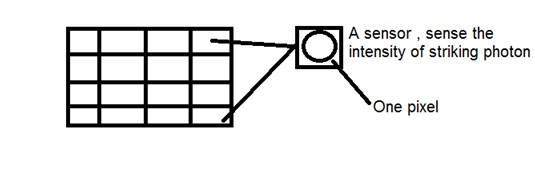
Эта ПЗС-матрица фактически имеет форму массива или прямоугольной сетки. Это как матрица с каждой ячейкой в ​​матрице, содержащей цензор, который измеряет интенсивность фотона.

Как и в случае с аналоговыми камерами, в случае с цифровым светом, когда на объект падает свет, он отражается назад после удара по объекту и может попасть внутрь камеры.

Каждый датчик матрицы ПЗС является аналоговым датчиком. Когда световые фотоны попадают на чип, он удерживается в виде небольшого электрического заряда в каждом фотодатчике. Реакция каждого датчика прямо равна количеству света или (фотонной) энергии, попадающей на поверхность датчика.

Поскольку мы уже определили изображение как двумерный сигнал и благодаря двумерному формированию матрицы CCD, полное изображение может быть получено из этой матрицы CCD.

У него ограниченное количество датчиков, и это означает, что он может зафиксировать ограниченную детализацию. Также каждый датчик может иметь только одно значение для каждой фотонной частицы, которая падает на него.

Таким образом, количество фотонов, поражающих (тока), подсчитывается и сохраняется. Для их точного измерения внешние КМОП-датчики также снабжены матрицей CCD.

Введение в пиксель

Значение каждого датчика матрицы CCD относится к каждому значению отдельного пикселя. Количество датчиков = количество пикселей. Это также означает, что каждый датчик может иметь только одно и только одно значение.

Хранение изображения

Заряды, хранящиеся в матрице ПЗС, преобразуются в напряжение по одному пикселю за раз. С помощью дополнительных цепей это напряжение преобразуется в цифровую информацию и затем сохраняется.

Каждая компания, которая производит цифровые фотоаппараты, изготавливает собственные ПЗС-датчики. Это включает в себя Sony, Mistubishi, Nikon, Samsung, Toshiba, FujiFilm, Canon и т. Д.

Помимо других факторов, качество получаемого изображения также зависит от типа и качества используемой матрицы CCD.

Камера Механизм

В этом уроке мы обсудим некоторые основные понятия камеры, такие как диафрагма, выдержка, выдержка, ISO, и мы обсудим коллективное использование этих понятий для получения хорошего изображения.

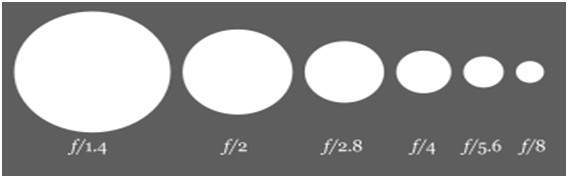
апертура

Апертура — это небольшое отверстие, которое позволяет свету проникать внутрь камеры. Вот изображение диафрагмы.

Вы увидите несколько маленьких лезвий, как вещи внутри отверстия. Эти лезвия создают восьмиугольную форму, которую можно открывать закрытым. И поэтому имеет смысл, что чем больше лопастей откроется, тем больше будет отверстие, из которого должен пройти свет. Чем больше отверстие, тем больше света может войти.

эффект

Эффект диафрагмы напрямую соответствует яркости и темноте изображения. Если отверстие диафрагмы широкое, это позволит большему количеству света проходить в камеру. Больше света приведет к большему количеству фотонов, что в конечном итоге приведет к более яркому изображению.

Пример этого показан ниже

Рассмотрим эти две фотографии

Тот, что справа, выглядит ярче, это означает, что когда он был захвачен камерой, диафрагма была широко открыта. По сравнению с другим изображением на левой стороне, которое является очень темным, по сравнению с первым, которое показывает, что, когда это изображение было снято, его апертура не была широко открыта.

Размер

Теперь давайте обсудим математику за апертурой. Размер апертуры обозначается значением af. И оно обратно пропорционально открытию отверстия.

Вот два уравнения, которые лучше всего объясняют эту концепцию.

Большой размер диафрагмы = малое значение f

Малый размер диафрагмы = большее значение f

Наглядно это можно представить как:

ставень

После проема появляется затвор. Свет, когда он пропускается из отверстия, падает прямо на затвор. Шторка на самом деле является крышкой, закрытым окном или может рассматриваться как занавес. Помните, когда мы говорим о матричном сенсоре CCD, на котором формируется изображение. Хорошо позади затвора находится датчик. Так что затвор — это единственное, что находится между формированием изображения и светом, когда он пропускается из апертуры.

Как только затвор открывается, свет падает на датчик изображения, и изображение формируется на массиве.

эффект

Если затвор позволяет свету проходить немного дольше, изображение будет ярче. Точно так же получается более темное изображение, когда затвору разрешено перемещаться очень быстро, и, следовательно, свет, который пропускается, имеет очень мало фотонов, а изображение, которое формируется на матрице ПЗС-матрицы, очень темное.

Затвор имеет еще две основные концепции:

• Скорость затвора

• Время затвора

Скорость затвора

Время затвора

Скорость затвора

Скорость затвора можно назвать количеством раз, когда затвор открывается или закрывается. Помните, мы не говорим о том, как долго затвор открывается или закрывается.

Время затвора

Время затвора можно определить как

Когда затвор открыт, то время ожидания, необходимое для его закрытия, называется временем затвора.

В данном случае мы не говорим о том, сколько раз затвор открывался или закрывался, но мы говорим о том, сколько времени он остается широко открытым.

Например:

Мы можем лучше понять эти две концепции таким образом. Это говорит о том, что затвор открывается 15 раз, а затем закрывается, и каждый раз он открывается на 1 секунду, а затем закрывается. В этом примере 15 — это скорость затвора, а 1 секунда — это время затвора.

отношения

Соотношение между скоростью затвора и временем затвора заключается в том, что они оба обратно пропорциональны друг другу.

Эта связь может быть определена в уравнении ниже.

Большая выдержка = меньше выдержки

Меньшая выдержка = больше выдержки.

Объяснение:

Чем меньше требуется времени, тем больше скорость. И чем больше требуется времени, тем меньше скорость.

Приложения

Эти два понятия вместе составляют множество приложений. Некоторые из них приведены ниже.

Быстро движущиеся объекты:

Если бы вы должны были захватить изображение быстро движущегося объекта, это может быть машина или что-то еще. Регулировка скорости затвора и его времени будет иметь большое значение.

Итак, чтобы сделать снимок, подобный этому, мы сделаем две поправки:

• Увеличить выдержку

• Уменьшить время затвора

Увеличить выдержку

Уменьшить время затвора

Что происходит, когда мы увеличиваем скорость затвора, чем больше раз, затвор будет открываться или закрываться. Это означает, что различные образцы света позволят проходить внутрь. А когда мы уменьшаем время затвора, это означает, что мы немедленно запечатлим сцену и закроем затвор затвора.

Если вы сделаете это, вы получите четкое изображение быстро движущегося объекта.

Чтобы понять это, мы рассмотрим этот пример. Предположим, вы хотите запечатлеть образ быстро движущегося водопада.

Вы устанавливаете выдержку в 1 секунду, и вы делаете снимок. Это то, что ты получаешь

Затем вы устанавливаете выдержку на более высокую скорость, и вы получаете.

Затем вы снова устанавливаете скорость затвора еще быстрее, и вы получаете.

На последнем изображении вы можете видеть, что мы увеличили скорость затвора до очень быстрой, это означает, что затвор открывается или закрывается за 200 секунд за 1 секунду, и мы получили четкое изображение.

ISO

Коэффициент ISO измеряется в цифрах. Это обозначает чувствительность света к камере. Если число ISO уменьшается, это означает, что наша камера менее чувствительна к свету, а если число ISO высокое, это означает, что она более чувствительна.

эффект

Чем выше ISO, тем ярче будет изображение. Если ISO установлен на 1600, изображение будет очень ярким и наоборот.

Побочный эффект

Если ISO увеличивается, шум на изображении также увеличивается. Сегодня большинство компаний-производителей камер работают над устранением шума на изображении, когда ISO настроен на более высокую скорость.

Концепция Пикселя

пиксель

Пиксель — это самый маленький элемент изображения. Каждый пиксель соответствует какому-либо одному значению. В 8-битном изображении серой шкалы значение пикселя находится в диапазоне от 0 до 255. Значение пикселя в любой точке соответствует интенсивности световых фотонов, падающих в эту точку. Каждый пиксель хранит значение, пропорциональное интенсивности света в этом конкретном месте.

PEL

Пиксель также известен как PEL. Вы можете лучше понять пиксель из рисунков, приведенных ниже.

На изображении выше могут быть тысячи пикселей, которые вместе составляют это изображение. Мы будем увеличивать это изображение до такой степени, чтобы мы могли видеть некоторые пиксельные деления. Это показано на изображении ниже.

На изображении выше могут быть тысячи пикселей, которые вместе составляют это изображение. Мы будем увеличивать это изображение до такой степени, чтобы мы могли видеть некоторые пиксельные деления. Это показано на изображении ниже.

Корабль связи с матрицей CCD

Мы видели, как образ формируется в матрице CCD. Таким образом, пиксель также может быть определен как

Наименьшее деление матрицы ПЗС также известно как пиксель.

Каждое деление матрицы ПЗС содержит значение в зависимости от интенсивности фотона, ударяющего в него. Это значение также можно назвать пикселем

Расчет общего количества пикселей

Мы должны определить изображение как двумерный сигнал или матрицу. Тогда в этом случае количество PEL будет равно числу строк, умноженному на количество столбцов.

Это может быть математически представлено ниже:

Общее количество пикселей = количество строк (X) количество столбцов

Или мы можем сказать, что количество (x, y) координатных пар составляет общее количество пикселей.

Мы рассмотрим более подробно в руководстве по типам изображений, как рассчитать пиксели в цветном изображении.

Уровень серого

Значение пикселя в любой точке обозначает интенсивность изображения в этом месте, что также называется уровнем серого.

Мы увидим более подробно о значении пикселей в хранилище изображений и учебнике по битам на пиксель, но сейчас мы просто рассмотрим концепцию значения только одного пикселя.

Значение пикселя. (0)

Как уже было определено в начале этого урока, каждый пиксель может иметь только одно значение, а каждое значение обозначает интенсивность света в этой точке изображения.

Теперь мы рассмотрим очень уникальное значение 0. Значение 0 означает отсутствие света. Это означает, что 0 обозначает темный, и это также означает, что когда пиксель имеет значение 0, это означает, что в этой точке будет сформирован черный цвет.

Посмотрите на эту матрицу изображений

0	0	0
0	0	0
0	0	0

Теперь эта матрица изображений заполнена нулями. Все пиксели имеют значение 0. Если бы мы рассчитали общее количество пикселей в этой матрице, это то, как мы собираемся это сделать.

Общее количество пикселей = общее количество из строк X всего № колонн

= 3 х 3

= 9

Это означает, что изображение будет сформировано с 9 пикселями, и это изображение будет иметь размер 3 строки и 3 столбца, и что наиболее важно, это изображение будет черным.

Полученное изображение будет примерно таким

Теперь, почему это изображение все черное. Потому что все пиксели в изображении имели значение 0.

Перспективная трансформация

Когда человеческие глаза видят близкие вещи, они выглядят больше, чем те, кто далеко. Это называется перспективой в общем смысле. Принимая во внимание, что преобразование — это передача объекта и т. Д. Из одного состояния в другое.

Итак, в целом, трансформация перспективы связана с преобразованием трехмерного мира в двумерное изображение. Тот же принцип, по которому работает человеческое зрение, и тот же принцип, по которому работает камера.

Мы подробно рассмотрим, почему это происходит, когда те объекты, которые находятся рядом с вами, выглядят больше, в то время как те, которые находятся далеко, выглядят меньше, даже если они выглядят больше, когда вы достигаете их.

Мы начнем это обсуждение с концепции системы отсчета:

Точка зрения:

Система отсчета — это в основном набор значений, относительно которых мы что-то измеряем.

5 систем отсчета

Чтобы проанализировать трехмерный мир / изображение / сцену, требуется 5 различных систем отсчета.

• объект

• Мир

• камера

• Образ

• пиксель

объект

Мир

камера

Образ

пиксель

Координатная рамка объекта

Координатная рамка объекта используется для моделирования объектов. Например, проверка, находится ли определенный объект в надлежащем месте относительно другого объекта. Это трехмерная система координат.

Мировая система координат

Мировая система координат используется для взаимосвязанных объектов в трехмерном мире. Это трехмерная система координат.

Координатная рамка камеры

Рамка координат камеры используется для связи объектов относительно камеры. Это трехмерная система координат.

Рамка координат изображения

Это не 3-я система координат, а 2-я система. Он используется для описания того, как трехмерные точки отображаются в плоскости двумерного изображения.

Пиксельная координатная рамка

Это также двумерная система координат. Каждый пиксель имеет значение координат пикселя.

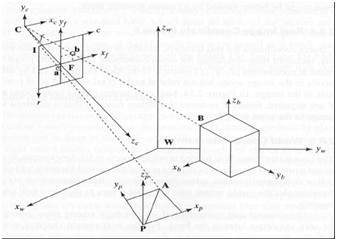
Преобразование между этими 5 кадрами

Вот как 3D-сцена превращается в 2d, с изображением пикселей.

Теперь мы объясним это понятие математически.

куда

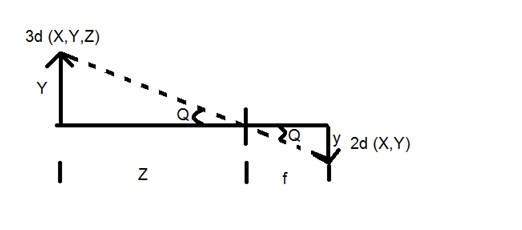
Y = 3d объект

y = 2d изображение

f = фокусное расстояние камеры

Z = расстояние между изображением и камерой

Теперь в этом преобразовании сформированы два разных угла, которые представлены Q.

Первый угол

Где минус обозначает, что изображение инвертировано. Второй угол, который формируется:

Сравнивая эти два уравнения, мы получаем

Из этого уравнения мы видим, что когда лучи света отражаются назад после удара от объекта, прошедшего от камеры, образуется инвертированное изображение.

Мы можем лучше понять это на этом примере.

Например

Расчет размера сформированного изображения

Предположим, что было снято изображение человека ростом 5 м, стоящего на расстоянии 50 м от камеры, и мы должны сказать, что размер изображения человека с камерой с фокусным расстоянием составляет 50 мм.

Решение:

Поскольку фокусное расстояние указано в миллиметрах, мы должны преобразовать каждую вещь в миллиметр, чтобы рассчитать ее.

Так,

Y = 5000 мм.

f = 50 мм.

Z = 50000 мм.

Положив значения в формулу, получим

= -5 мм.

Опять же, знак минус указывает, что изображение перевернуто.

Концепция битов на пиксель

Bpp или бит на пиксель обозначает количество бит на пиксель. Количество различных цветов в изображении зависит от глубины цвета или битов на пиксель.

Биты по математике:

Это как играть с двоичными битами.

Сколько чисел можно представить одним битом.

0

1

Сколько двухбитных комбинаций можно сделать.

00

01

10

11

Если мы разработаем формулу для расчета общего числа комбинаций, которые могут быть сделаны из битов, это будет так.

Где bpp обозначает биты на пиксель. Поместите 1 в формулу, вы получите 2, поставьте 2 в формуле, вы получите 4. Он растет в геометрической прогрессии.

Количество разных цветов:

Как мы уже говорили в начале, количество разных цветов зависит от количества бит на пиксель.

Таблица для некоторых битов и их цвета приведена ниже.

Бит на пиксель	Количество цветов
1 пп	2 цвета
2 bpp	4 цвета
3 пп	8 цветов
4 п.н.	16 цветов
5 пп	32 цвета
6 пп	64 цвета
7 пп	128 цветов
8 п.н.	256 цветов
10 пп	1024 цвета
16 п.н.	65536 цветов
24 п.н.	16777216 цветов (16,7 миллионов цветов)
32 п.н.	4294967296 цветов (4294 миллиона цветов)

Эта таблица показывает различные биты на пиксель и количество цвета, которое они содержат.

Оттенки

Вы можете легко заметить характер экспоненциального роста. Известное серое изображение имеет 8 бит на дюйм, что означает, что оно имеет 256 различных цветов или 256 оттенков.

Оттенки могут быть представлены как:

Цветные изображения обычно имеют формат 24 бит / с или 16 бит / с.

Мы узнаем больше о других цветовых форматах и ​​типах изображений в руководстве по типам изображений.

Цветовые значения:

Ранее мы видели в руководстве по понятию пиксель, что значение 0 пикселей обозначает черный цвет.

Черный цвет:

Помните, что значение 0 пикселей всегда обозначает черный цвет. Но нет фиксированного значения, обозначающего белый цвет.

Белый цвет:

Значение, обозначающее белый цвет, может быть рассчитано как:

В случае 1 bpp, 0 обозначает черный, а 1 обозначает белый.

В случае 8 bpp, 0 обозначает черный, а 255 обозначает белый.

Серый цвет:

Когда вы вычисляете значение черного и белого цвета, вы можете рассчитать значение пикселя серого цвета.

Серый цвет на самом деле является серединой черного и белого. Это сказало,

В случае 8bpp значение пикселя, обозначающее серый цвет, составляет 127 или 128bpp (если считать от 1, а не от 0).

Требования к хранилищу изображений

После обсуждения битов на пиксель, теперь у нас есть все, что нам нужно, чтобы рассчитать размер изображения.

Размер изображения

Размер изображения зависит от трех вещей.

• Количество рядов

• Число столбцов

• Количество бит на пиксель

Количество рядов

Число столбцов

Количество бит на пиксель

Формула для расчета размера приведена ниже.

Размер изображения = строки * столбцы * bpp

Это означает, что если у вас есть изображение, скажем так:

Предполагая, что в нем 1024 строки и 1024 столбца. А поскольку это изображение в оттенках серого, оно имеет 256 различных оттенков серого или биты на пиксель. Затем, поместив эти значения в формулу, получим

Размер изображения = строки * столбцы * bpp

= 1024 * 1024 * 8

= 8388608 бит.

Но так как это не стандартный ответ, который мы распознаем, он будет преобразован в наш формат.

Преобразование его в байты = 8388608/8 = 1048576 байтов.

Преобразование в килобайты = 1048576/1024 = 1024 КБ.

Преобразование в мегабайты = 1024/1024 = 1 Мб.

Вот как рассчитывается размер изображения и сохраняется. Теперь в формуле, если вам задан размер изображения и количество бит на пиксель, вы также можете вычислить строки и столбцы изображения, при условии, что изображение является квадратным (те же строки и тот же столбец).

Типы изображений

Существует много типов изображений, и мы подробно рассмотрим различные типы изображений и распределение цветов в них.

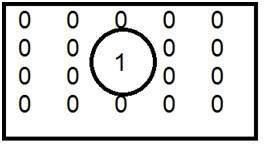
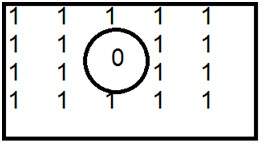
Двоичное изображение

Двоичное изображение, как его называют, содержит только два пиксельных значения.

0 и 1.

В нашем предыдущем уроке битов на пиксель мы подробно объяснили это о представлении значений пикселей их соответствующим цветам.

Здесь 0 относится к черному цвету, а 1 относится к белому цвету. Он также известен как монохромный.

Черно-белое изображение:

Получающееся изображение, следовательно, состоит только из черно-белого цвета и, следовательно, также может называться черно-белым изображением.

Нет уровня серого

Одна из интересных особенностей этого двоичного изображения в том, что в нем нет уровня серого. В нем встречаются только два цвета: черный и белый.

Формат

Бинарные изображения имеют формат PBM (Portable bit map)

2, 3, 4, 5, 6-битный цветовой формат

Изображения с цветным форматом 2, 3, 4, 5 и 6 бит в настоящее время широко не используются. Они использовались в старые времена для старых телевизионных дисплеев или мониторов.

Но каждый из этих цветов имеет более двух уровней серого и, следовательно, имеет серый цвет в отличие от двоичного изображения.

В 2 битах 4, в 3 битах 8, в 4 битах 16, в 5 битах 32, в 6 битах присутствуют 64 разных цвета.

8-битный цветовой формат

8-битный цветовой формат является одним из самых известных форматов изображений. В нем 256 разных оттенков. Это широко известно как изображение в градациях серого.

Диапазон цветов в 8 битах варьируется от 0 до 255. Где 0 обозначает черный, 255 обозначает белый, а 127 обозначает серый цвет.

Этот формат изначально использовался ранними моделями операционных систем UNIX и ранних цветных Macintoshes.

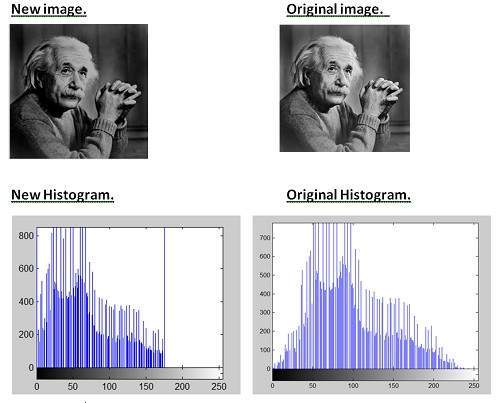
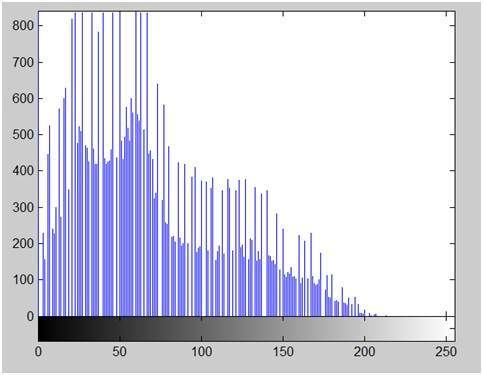
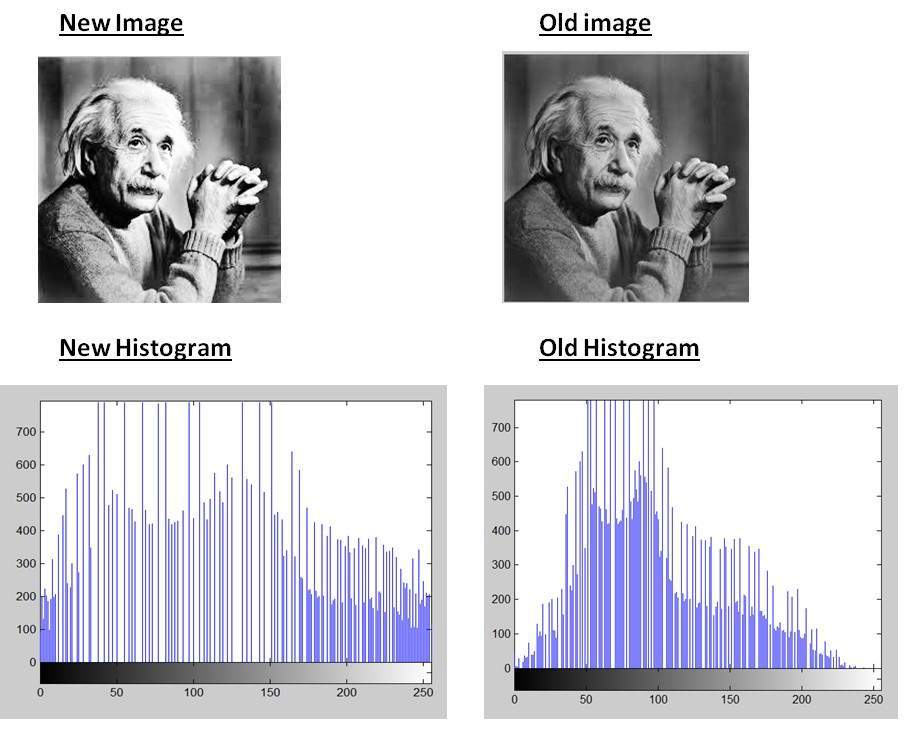
Изображение Эйнштейна в оттенках серого показано ниже:

Формат

Формат этих изображений — PGM (Portable Grey Map).

Этот формат не поддерживается по умолчанию из окон. Чтобы увидеть изображение в оттенках серого, вам необходимо иметь средство просмотра изображений или набор инструментов для обработки изображений, например Matlab.

За серым изображением:

Как мы уже несколько раз объясняли в предыдущих уроках, что изображение — это не что иное, как двумерная функция, и может быть представлено двумерным массивом или матрицей. Таким образом, в случае изображения Эйнштейна, показанного выше, сзади будет двухмерная матрица со значениями в диапазоне от 0 до 255.

Но это не относится к цветным изображениям.

16-битный цветовой формат

Это цветной формат изображения. В нем 65,536 разных цветов. Он также известен как высокий цветовой формат.

Это использовалось Microsoft в их системах, которые поддерживают более чем 8-битный цветовой формат. Теперь в этом 16-битном формате и следующем формате, который мы собираемся обсудить, который является 24-битным форматом, оба являются цветовым форматом.

Распределение цвета в цветном изображении не так просто, как в черно-белом изображении.

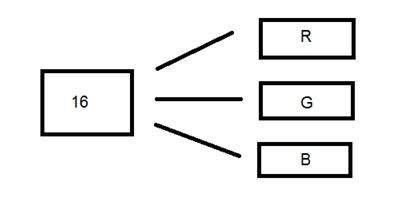
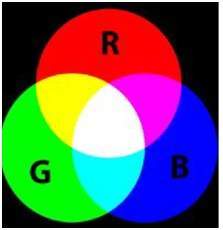
16-битный формат фактически делится на три следующих формата: красный, зеленый и синий. Знаменитый (RGB) формат.

Это наглядно представлено на изображении ниже.

Теперь возникает вопрос, как бы распределить 16 на три. Если вы делаете это так,

5 бит для R, 5 бит для G, 5 бит для B

Тогда остается один бит в конце.

Таким образом, распределение 16 бит было сделано следующим образом.

5 бит для R, 6 бит для G, 5 бит для B.

Дополнительный бит, который остался позади, добавляется в зеленый бит. Потому что зеленый — это цвет, который больше всего успокаивает глаза во всех этих трех цветах.

Обратите внимание, что за распространением следуют не все системы. Некоторые ввели альфа-канал в 16 бит.

Другой дистрибутив 16-битного формата выглядит так:

4 бита для R, 4 бита для G, 4 бита для B, 4 бита для альфа-канала.

Или некоторые распространяют это так

5 бит для R, 5 бит для G, 5 бит для B, 1 бит для альфа-канала.

24-битный цветовой формат

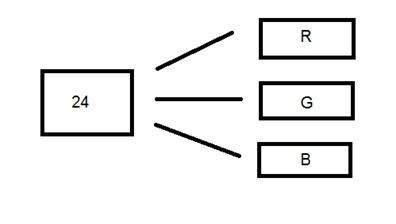
24-битный цветовой формат, также известный как формат истинного цвета. Как и в 16-битном цветном формате, в 24-битном цветном формате 24-битные снова распределяются в трех различных форматах: красном, зеленом и синем.

Поскольку 24 делится поровну на 8, то оно распределяется поровну между тремя разными цветовыми каналами.

Их распределение таково.

8 бит для R, 8 бит для G, 8 бит для B.

За 24-битным изображением.

В отличие от 8-битного серого изображения, которое имеет одну матрицу позади, 24-битное изображение имеет три разные матрицы R, G, B.

Формат

Это наиболее распространенный используемый формат. Его формат — PPM (Portable pixMap), который поддерживается операционной системой Linux. Знаменитые окна имеют собственный формат BMP (Bitmap).

Преобразование цветовых кодов

В этом уроке мы увидим, как различные цветовые коды можно комбинировать для создания других цветов, и как мы можем преобразовать цветовые коды RGB в шестнадцатеричные и наоборот.

Разные цветовые коды

Все цвета здесь имеют 24-битный формат, то есть каждый цвет содержит 8 бит красного, 8 бит зеленого и 8 бит синего. Или мы можем сказать, что каждый цвет состоит из трех разных частей. Вам просто нужно изменить количество этих трех порций, чтобы сделать любой цвет.

Двоичный цветовой формат

Черный цвет

Образ:

Десятичный код:

(0,0,0)

Объяснение:

Как было объяснено в предыдущих уроках, в 8-битном формате 0 обозначает черный. Поэтому, если нам нужно сделать чистый черный цвет, мы должны сделать все три части R, G, B равными 0.

Белый цвет

Образ:

Десятичный код:

(255255255)

Объяснение:

Поскольку каждая часть R, G, B является 8-битной частью. Таким образом, в 8-битном белом цвете формируется 255. Это объясняется в учебнике по пикселям. Таким образом, чтобы сделать белый цвет, мы устанавливаем каждую порцию на 255, и вот как мы получили белый цвет. Установив для каждого значения 255, мы получаем общее значение 255, то есть цвет становится белым.

Цветовая модель RGB:

Красный цвет

Образ:

Десятичный код:

(255,0,0)

Объяснение:

Так как нам нужен только красный цвет, мы обнуляем оставшиеся две части, зеленые и синие, и устанавливаем для красной части максимум, равный 255.

Цвет: зеленый

Образ:

Десятичный код:

(0,255,0)

Объяснение:

Поскольку нам нужен только зеленый цвет, мы обнуляем остальные две части, которые являются красной и синей, и устанавливаем для зеленой части ее максимум, равный 255.

Цвет синий

Образ:

Десятичный код:

(0,0,255)

Объяснение:

Поскольку нам нужен только синий цвет, мы обнуляем остальные две части, которые являются красной и зеленой, и устанавливаем для синей части ее максимум, равный 255

Серый цвет:

Цвет: серый

Образ:

Десятичный код:

(128128128)

Объяснение:

Как мы уже определили в нашем уроке по пикселям, этот серый цвет на самом деле является средней точкой. В 8-битном формате средняя точка равна 128 или 127. В этом случае мы выбираем 128. Таким образом, мы устанавливаем для каждой части ее среднюю точку, равную 128, и в результате получается общее среднее значение, и мы получаем серый цвет.

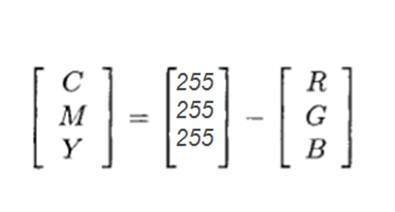
Цветовая модель CMYK:

CMYK — это другая цветовая модель, где c обозначает голубой, m обозначает пурпурный, y обозначает желтый и k обозначает черный. Модель CMYK обычно используется в цветных принтерах, в которых используются два цветных картера. Один состоит из CMY, а другой состоит из черного цвета.

Цвета CMY также могут быть сделаны путем изменения количества или доли красного, зеленого и синего.

Цвет: голубой

Образ:

Десятичный код:

(0255255)

Объяснение:

Голубой цвет формируется из комбинации двух разных цветов: зеленого и синего. Таким образом, мы устанавливаем эти два на максимум и обнуляем часть красного. И мы получаем голубой цвет.

Цвет: пурпурный

Образ:

Десятичный код:

(255,0,255)

Объяснение:

Пурпурный цвет образуется из комбинации двух разных цветов: красного и синего. Таким образом, мы устанавливаем эти два на максимум и обнуляем порцию зеленого. И мы получаем пурпурный цвет.

Цвет: желтый

Образ:

Десятичный код:

(255,255,0)

Объяснение:

Желтый цвет сформирован из комбинации двух разных цветов, которые являются красным и зеленым. Таким образом, мы устанавливаем эти два на максимум и обнуляем порцию синего цвета. И мы получаем желтый цвет.

преобразование

Теперь мы увидим, как цвета преобразуются из одного формата в другой.

Преобразование из RGB в шестнадцатеричный код:

Преобразование из Hex в rgb выполняется с помощью этого метода:

• Возьми цвет. Например: белый = (255, 255, 255).

• Возьмите первую порцию, например, 255.

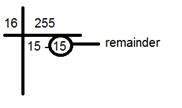
• Разделите это на 16. Вот так:

• 

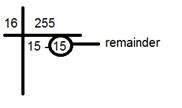
• Возьмите два числа под линией, коэффициент и остаток. В этом случае это 15 15, что является FF.

• Повторите шаг 2 для следующих двух частей.

• Объедините весь шестнадцатеричный код в один.

Возьми цвет. Например: белый = (255, 255, 255).

Возьмите первую порцию, например, 255.

Разделите это на 16. Вот так:

Возьмите два числа под линией, коэффициент и остаток. В этом случае это 15 15, что является FF.

Повторите шаг 2 для следующих двух частей.

Объедините весь шестнадцатеричный код в один.

Ответ: #FFFFFF

Преобразование из Hex в RGB:

Преобразование из шестнадцатеричного кода в десятичный формат rgb выполняется таким образом.

Возьмите шестнадцатеричное число. Например: #FFFFFF

Разбейте это число на 3 части: FF FF FF

Возьмите первую часть и разделите ее компоненты: F F

Конвертировать каждую часть отдельно в двоичную форму: (1111) (1111)

Теперь объедините отдельные двоичные файлы в один: 11111111

Преобразовать этот двоичный файл в десятичный: 255

Теперь повторите шаг 2, еще два раза.

Значение входит в первый шаг R, второй G, а третий принадлежит B.

Ответ: (255, 255, 255)

Общие цвета и их шестнадцатеричный код приведены в этой таблице.

цвет	Шестнадцатеричный код
черный	# 000000
белый	#FFFFFF
Серый	# 808080
красный	# FF0000
зеленый	# 00FF00
синий	# 0000FF
Cyan	# 00FFFF
фуксин	# FF00FF
желтый	# FFFF00

Оттенки серого в RGB

Мы уже определили цветовую модель RGB и формат серой шкалы в нашем уроке типов изображений. Теперь мы преобразуем цветное изображение в изображение в градациях серого. Есть два метода, чтобы преобразовать это. У обоих есть свои достоинства и недостатки. Методы:

• Средний метод

• Взвешенный метод или метод светимости

Средний метод

Взвешенный метод или метод светимости

Средний метод

Средний метод является наиболее простым. Вам просто нужно взять в среднем три цвета. Поскольку это RGB-изображение, это означает, что вы добавили r с g к b, а затем разделили его на 3, чтобы получить желаемое изображение в градациях серого.

Это сделано таким образом.

Оттенки серого = (R + G + B / 3)

Например:

Если у вас есть цветное изображение, подобное изображенному выше, и вы хотите преобразовать его в оттенки серого, используя метод усреднения. Следующий результат появится.

объяснение

Есть одна вещь, чтобы быть уверенным, что что-то происходит с оригинальными работами. Это означает, что наш средний метод работает. Но результаты оказались не такими, как ожидалось. Мы хотели преобразовать изображение в градации серого, но это оказалось довольно черное изображение.

проблема

Эта проблема возникает из-за того, что мы берем среднее из трех цветов. Поскольку три разных цвета имеют три разные длины волны и имеют свой собственный вклад в формирование изображения, поэтому мы должны брать среднее значение в соответствии с их вкладом, а не делать это в среднем, используя метод усреднения. Прямо сейчас то, что мы делаем, это,

33% красного, 33% зеленого, 33% синего

Мы берем 33% каждого, это означает, что каждая часть имеет одинаковый вклад в изображение. Но на самом деле это не так. Решение этой проблемы было дано методом светимости.

Взвешенный метод или метод светимости

Вы видели проблему, которая возникает в среднем методе. Взвешенный метод имеет решение этой проблемы. Поскольку красный цвет имеет большую длину волны из всех трех цветов, а зеленый — это цвет, который имеет не только меньшую длину волны, чем красный, но и зеленый — это цвет, который дает более успокаивающий эффект для глаз.

Это означает, что мы должны уменьшить вклад красного цвета, увеличить вклад зеленого цвета и поместить вклад синего цвета между этими двумя.

Итак, новое уравнение этой формы:

Новое изображение в градациях серого = ((0,3 * R) + (0,59 * G) + (0,11 * B)).

Согласно этому уравнению, красный дает 30%, зеленый — 59%, что больше во всех трех цветах, а синий — 11%.

Применяя это уравнение к изображению, получим

Исходное изображение:

Изображение в градациях серого:

объяснение

Как вы можете видеть здесь, изображение теперь правильно преобразовано в оттенки серого с использованием метода взвешивания. По сравнению с результатом среднего метода, это изображение является более ярким.

Концепция отбора проб

Преобразование аналогового сигнала в цифровой сигнал:

Выход большинства датчиков изображения является аналоговым сигналом, и мы не можем применить к нему цифровую обработку, потому что мы не можем его сохранить. Мы не можем сохранить его, потому что он требует бесконечной памяти для хранения сигнала, который может иметь бесконечные значения.

Таким образом, мы должны преобразовать аналоговый сигнал в цифровой сигнал.

Чтобы создать цифровое изображение, нам нужно преобразовать непрерывные данные в цифровую форму. Есть два шага, в которых это делается.

• отбор проб

• квантование

отбор проб

квантование

Мы обсудим выборку сейчас, а квантование будет обсуждаться позже, а пока мы немного обсудим разницу между этими двумя и необходимость этих двух шагов.

Основная идея:

Основная идея преобразования аналогового сигнала в цифровой:

преобразовать обе его оси (х, у) в цифровой формат.

Поскольку изображение непрерывно не только по своим координатам (ось x), но и по его амплитуде (ось y), поэтому часть, которая занимается оцифровкой координат, называется выборкой. И часть, которая имеет дело с оцифровкой амплитуды, известна как квантование.

Отбор проб.

Выборка уже была представлена ​​в нашем уроке введения в сигналы и систему. Но мы собираемся обсудить здесь больше.

Вот что мы обсудили из выборки.

Термин «выборка» относится к отбору проб

Оцифровываем ось х в выборке

Это делается на независимой переменной

В случае уравнения y = sin (x) это делается для переменной x

Далее он делится на две части: восходящий и нисходящий

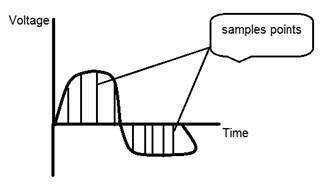
Если вы посмотрите на рисунок выше, вы увидите, что в сигнале есть некоторые случайные изменения. Эти изменения происходят из-за шума. При выборке мы уменьшаем этот шум, отбирая образцы. Очевидно, что чем больше выборок мы берем, тем лучше будет качество изображения, тем больше будет шума, и наоборот.

Однако, если вы берете выборку по оси x, сигнал не преобразуется в цифровой формат, если только вы не берете выборку по оси y, которая известна как квантование. Чем больше выборок в конечном итоге означает, что вы собираете больше данных, а в случае изображения — больше пикселей.

Отношение корабль с пикселями

Поскольку пиксель является наименьшим элементом в изображении. Общее количество пикселей в изображении может быть рассчитано как

Пиксели = общее количество строк * общее количество столбцов.

Допустим, у нас всего 25 пикселей, это означает, что у нас квадратное изображение 5 X 5. Тогда, как мы уже говорили выше при выборке, что больше выборок в конечном итоге приводит к большему количеству пикселей. Таким образом, это означает, что из нашего непрерывного сигнала мы взяли 25 выборок по оси x. Это относится к 25 пикселям этого изображения.

Это приводит к другому выводу, что, поскольку пиксель также является наименьшим делением матрицы ПЗС. Таким образом, это означает, что он также связан с массивом CCD, что можно объяснить следующим образом.

Связь с массивом CCD

Количество датчиков в матрице ПЗС прямо равно количеству пикселей. И поскольку мы пришли к выводу, что количество пикселей прямо равно количеству отсчетов, это означает, что число отсчетов прямо равно количеству датчиков в матрице ПЗС.

Передискретизации.

В начале мы определили, что выборка делится на два типа. Что вверх по выборке и вниз по выборке. Повышенная выборка также называется избыточной выборкой.

Передискретизация имеет очень глубокое применение в обработке изображений, которая называется Zooming.

Масштабирование

Мы официально представим масштабирование в следующем уроке, но сейчас мы кратко объясним масштабирование.

Масштабирование относится к увеличению количества пикселей, поэтому при увеличении изображения вы увидите больше деталей.

Увеличение количества пикселей осуществляется за счет передискретизации. Один из способов увеличения или увеличения выборки заключается в оптическом увеличении с помощью движения объектива и последующем захвате изображения. Но мы должны сделать это, как только изображение будет снято.

Существует разница между масштабированием и выборкой.

Концепция та же, то есть увеличение образцов. Но ключевое отличие состоит в том, что, хотя дискретизация выполняется для сигналов, масштабирование выполняется для цифрового изображения.

Разрешение пикселей

Прежде чем мы определим разрешение в пикселях, необходимо определить пиксель.

пиксель

Мы уже определили пиксель в нашем руководстве по понятию пиксель, в котором мы определяем пиксель как наименьший элемент изображения. Мы также определили, что пиксель может хранить значение, пропорциональное интенсивности света в этом конкретном месте.

Теперь, поскольку мы определили пиксель, мы собираемся определить, что такое разрешение.

разрешение

Разрешение может быть определено многими способами. Такие как разрешение пикселей, пространственное разрешение, временное разрешение, спектральное разрешение. Из которых мы будем обсуждать разрешение пикселей.

Вы, наверное, видели, что в ваших собственных настройках компьютера разрешение монитора составляет 800 x 600, 640 x 480 и т. Д.

В разрешении пикселей термин разрешение относится к общему количеству пикселей в цифровом изображении. Например. Если изображение имеет M строк и N столбцов, его разрешение можно определить как MX N.

Если мы определяем разрешение как общее количество пикселей, то разрешение пикселей можно определить с помощью набора из двух чисел. Первое число — ширина изображения или пикселей в столбцах, а второе — высота изображения или пикселей в ширине.

Можно сказать, что чем выше разрешение в пикселях, тем выше качество изображения.

Мы можем определить разрешение изображения в пикселях как 4500 X 5500.

мегапикселей

Мы можем рассчитать мегапиксели камеры, используя разрешение в пикселях.

Колонки пикселей (ширина) X строк пикселей (высота) / 1 млн.

Размер изображения может быть определен его разрешением в пикселях.

Размер = разрешение в пикселях X bpp (бит на пиксель)

Расчет мегапикселей камеры

Допустим, у нас есть изображение размером: 2500 X 3192.

Его разрешение в пикселях = 2500 * 3192 = 7982350 байтов.

Разделив его на 1 миллион = 7,9 = 8 мегапикселей (приблизительно).

Соотношение сторон

Другая важная концепция с разрешением пикселей — это соотношение сторон.

Соотношение сторон — это соотношение между шириной изображения и его высотой. Обычно это объясняется двумя числами, разделенными двоеточием (8: 9). Это соотношение отличается на разных изображениях и на разных экранах. Общие соотношения сторон:

1,33: 1, 1,37: 1, 1,43: 1, 1,50: 1, 1,56: 1, 1,66: 1, 1,75: 1, 1,78: 1, 1,85: 1, 2,00: 1 и т. Д.

Преимущество:

Соотношение сторон поддерживает баланс между отображением изображения на экране, то есть поддерживает соотношение между горизонтальными и вертикальными пикселями. Это не позволяет искажать изображение при увеличении соотношения сторон.

Например:

Это образец изображения, который имеет 100 строк и 100 столбцов. Если мы хотим сделать меньше, и условие состоит в том, что качество остается тем же самым или иначе изображение не искажается, вот как это происходит.

Исходное изображение:

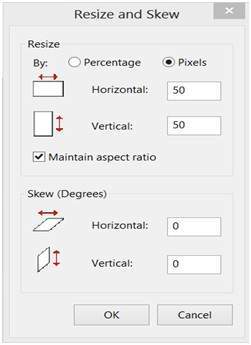
Изменение строк и столбцов путем поддержания соотношения сторон в MS Paint.

Результат

Меньшее изображение, но с тем же балансом.

Вы, вероятно, видели соотношение сторон в видео проигрывателях, где вы можете настроить видео в соответствии с вашим разрешением экрана.

Нахождение размеров изображения по соотношению сторон:

Соотношение сторон говорит нам много вещей. С помощью соотношения сторон вы можете рассчитать размеры изображения вместе с размером изображения.

Например

Если вам дано изображение с соотношением сторон 6: 2 изображения с разрешением 480000 пикселей, то это изображение в оттенках серого.

И вас просят рассчитать две вещи.

• Разрешить разрешение в пикселях для расчета размеров изображения

• Рассчитать размер изображения

Разрешить разрешение в пикселях для расчета размеров изображения

Рассчитать размер изображения

Решение:

Дано:

Соотношение сторон: c: r = 6: 2

Разрешение пикселей: c * r = 480000

Биты на пиксель: изображение в градациях серого = 8 бит на пиксель

Найти:

Количество рядов =?

Количество столбцов =?

Решаем первую часть:

Решение 2-й части:

Размер = строки * столбцы * bpp

Размер изображения в битах = 400 * 1200 * 8 = 3840000 бит

Размер изображения в байтах = 480000 байтов

Размер изображения в килобайтах = 48 кб (приблизительно).

Концепция масштабирования

В этом уроке мы собираемся представить концепцию масштабирования и общие методы, которые используются для масштабирования изображения.

Масштабирование

Масштабирование просто означает увеличение изображения в том смысле, что детали на изображении стали более видимыми и четкими. Масштабирование изображения имеет множество широких применений, начиная от масштабирования объектива фотоаппарата до масштабирования изображения в Интернете и т. Д.

Например

увеличено в

Вы можете увеличить что-то в два этапа.

Первый шаг включает масштабирование перед съемкой определенного изображения. Это известно как предварительная обработка зума. Этот зум включает в себя аппаратные и механические движения.

Вторым шагом является увеличение масштаба изображения после захвата изображения. Это делается с помощью множества различных алгоритмов, в которых мы манипулируем пикселями для увеличения требуемой части.

Мы обсудим их подробно в следующем уроке.

Оптический Zoom против цифрового Zoom

Эти два типа увеличения поддерживаются камерами.

Оптический зум:

Оптический зум достигается с помощью движения объектива вашей камеры. Оптический зум на самом деле настоящий зум. Результат оптического увеличения намного лучше, чем цифрового увеличения. При оптическом увеличении изображение увеличивается объективом таким образом, что объекты на изображении оказываются ближе к камере. При оптическом увеличении объектив физически расширяется для увеличения или увеличения объекта.

Цифровое увеличение:

Цифровой зум — это в основном обработка изображений внутри камеры. Во время цифрового увеличения центр изображения увеличивается, а края изображения обрезаются. Из-за увеличенного центра, похоже, что объект находится ближе к вам.

При цифровом увеличении пиксели расширяются, из-за чего ухудшается качество изображения.

Тот же эффект цифрового зума можно увидеть после того, как изображение пропущено через ваш компьютер с помощью набора инструментов / программного обеспечения для обработки изображений, такого как Photoshop.

На следующем рисунке показан результат цифрового увеличения, выполненного одним из следующих способов, приведенных ниже в методах масштабирования.

Теперь, когда мы опираемся на цифровую обработку изображений, мы не будем фокусироваться на том, как оптическое масштабирование изображения можно использовать с помощью объектива или другого материала. Скорее мы сосредоточимся на методах, позволяющих увеличить цифровое изображение.

Методы масштабирования:

Хотя есть много методов, которые делают эту работу, но мы собираемся обсудить наиболее распространенные из них здесь.

Они перечислены ниже.

• Пиксельная репликация или (интерполяция ближайшего соседа)

• Метод удержания нулевого порядка

• Масштабирование K раз

Пиксельная репликация или (интерполяция ближайшего соседа)

Метод удержания нулевого порядка

Масштабирование K раз

Все эти три метода официально представлены в следующем уроке.

Методы масштабирования

В этом уроке мы собираемся официально представить три метода масштабирования, которые были введены в уроке Введение в масштабирование.

методы

• Пиксельная репликация или (интерполяция ближайшего соседа)

• Метод удержания нулевого порядка

• Масштабирование K раз

Пиксельная репликация или (интерполяция ближайшего соседа)

Метод удержания нулевого порядка

Масштабирование K раз

Каждый из методов имеет свои преимущества и недостатки. Мы начнем с обсуждения репликации пикселей.

Метод 1: Репликация пикселей:

Вступление:

Он также известен как интерполяция ближайшего соседа. Как следует из названия, в этом методе мы просто копируем соседние пиксели. Как мы уже обсуждали в учебнике по сэмплированию, это увеличение не что иное, как увеличение количества выборок или пикселей. Этот алгоритм работает по тому же принципу.

За работой:

В этом методе мы создаем новые пиксели из уже заданных пикселей. Каждый пиксель реплицируется в этом методе n раз по строкам и столбцам, и вы получаете увеличенное изображение. Это так просто.

Например:

Если у вас есть изображение из 2 строк и 2 столбцов, и вы хотите увеличить его дважды или 2 раза с помощью пиксельной репликации, вот как это можно сделать.

Для лучшего понимания изображение было взято в виде матрицы со значениями пикселей изображения.

1	2
3	4

Изображение выше имеет две строки и два столбца, мы сначала увеличим его по размеру строки.

Масштабирование строк:

Когда мы масштабируем его по строкам, мы просто скопируем пиксели строк в соседнюю новую ячейку.

Вот как это будет сделано.

1	1	2	2
3	3	4	4

Как вы можете это сделать в приведенной выше матрице, каждый пиксель дублируется в строках дважды.

Увеличение размера столбца:

Следующим шагом является копирование каждого столбца пикселей, так что мы просто скопируем пиксель столбца в соседний новый столбец или просто под ним.

Вот как это будет сделано.

1	1	2	2
1	1	2	2
3	3	4	4
3	3	4	4

Новый размер изображения:

Как видно из приведенного выше примера, исходное изображение из 2 строк и 2 столбцов было преобразовано в 4 строки и 4 столбца после увеличения. Это означает, что новое изображение имеет размеры

(Строки исходного изображения * коэффициент масштабирования, столбцы исходного изображения * коэффициент масштабирования)

Преимущества и недостатки:

Одним из преимуществ этой техники масштабирования является то, что она очень проста. Вам просто нужно скопировать пиксели и больше ничего.

Недостаток этого метода в том, что изображение было увеличено, но изображение получилось очень размытым. И с увеличением коэффициента масштабирования изображение становилось все более размытым. Это в конечном итоге приведет к полностью размытому изображению.

Способ 2: удержание нулевого порядка

Вступление

Метод удержания нулевого порядка — это еще один метод масштабирования. Это также известно как увеличение масштаба изображения дважды. Потому что это может только увеличить в два раза. В следующем примере мы увидим, почему он это делает.

За работой

В методе удержания нулевого порядка мы выбираем два соседних элемента из строк соответственно, а затем добавляем их, делим результат на два и помещаем их результат между этими двумя элементами. Сначала мы делаем этот ряд мудрым, а затем мы делаем этот столбец мудрым.

Например

Давайте возьмем изображение размеров 2 строк и 2 столбцов и дважды увеличим его, используя удержание в нулевом порядке.

1	2
3	4

Сначала мы будем увеличивать его по ряду, а затем по столбцам.

Масштабирование строк

1	1	2
3	3	4

Когда мы берем первые два числа: (2 + 1) = 3, а затем делим его на 2, мы получаем 1,5, которое приближается к 1. Тот же метод применяется в строке 2.

Мудрое масштабирование столбцов

1	1	2
2	2	3
3	3	4

Мы берем два значения пикселей соседних столбцов, которые равны 1 и 3. Мы добавляем их и получаем 4. Затем 4 делится на 2, и мы получаем 2, которое помещается между ними. Один и тот же метод применяется во всех столбцах.

Новый размер изображения

Как видно, размеры нового изображения 3 x 3, а размеры исходного изображения 2 x 2. Таким образом, это означает, что размеры нового изображения основаны на следующей формуле

(2 (количество строк) минус 1) X (2 (количество столбцов) минус 1)

Преимущества и недостатки.

Одно из преимуществ этого метода масштабирования в том, что он не создает размытое изображение по сравнению с методом интерполяции ближайшего соседа. Но у него также есть недостаток, заключающийся в том, что он может работать только на степени 2. Это можно продемонстрировать здесь.

Причина двойного увеличения:

Рассмотрим изображение выше из 2 строк и 2 столбцов. Если нам нужно увеличить его 6 раз, используя метод удержания нулевого порядка, мы не сможем это сделать. Как формула показывает нам это.

Это может только увеличить степень 2 2,4,8,16,32 и так далее.

Даже если вы попытаетесь увеличить его, вы не сможете. Потому что сначала, когда вы увеличите его дважды, результат будет таким же, как показано в столбце, с масштабированием, равным 3х3. Затем вы снова увеличите масштаб и получите размеры, равные 5 x 5. Теперь, если вы сделаете это снова, вы получите размеры, равные 9 x 9.

Тогда как по вашей формуле ответ должен быть 11×11. Поскольку (6 (2) минус 1) X (6 (2) минус 1) дает 11 х 11.

Способ 3: увеличение K-Times

Вступление:

K раз — третий метод масштабирования, который мы собираемся обсудить. Это один из самых совершенных алгоритмов масштабирования, обсуждавшихся до сих пор. Он обслуживает задачи как двойного масштабирования, так и репликации пикселей. K в этом алгоритме масштабирования обозначает коэффициент масштабирования.

За работой:

Это работает так

Прежде всего, вам нужно взять два смежных пикселя, как вы делали это дважды. Затем вы должны вычесть меньшее из большего. Мы называем этот вывод (OP).

Разделите выход (OP) с коэффициентом масштабирования (K). Теперь вы должны добавить результат к меньшему значению и поместить результат между этими двумя значениями.

Снова добавьте значение OP к значению, которое вы только что поместили, и поместите его снова рядом с предыдущим введенным значением. Вы должны делать это, пока не поместите в него значения k-1.

Повторите тот же шаг для всех строк и столбцов, и вы получите увеличенные изображения.

Например:

Предположим, у вас есть изображение из 2 строк и 3 столбцов, которое приведено ниже. И вы должны увеличить его три или три раза.

15	30	15
30	15	30

К в этом случае составляет 3. К = 3.

Количество значений, которые должны быть вставлены, равно k-1 = 3-1 = 2.

Масштабирование строк

Возьмите первые два соседних пикселя. Которые 15 и 30.

Вычтите 15 из 30. 30-15 = 15.

Разделите 15 на k. 15 / k = 15/3 = 5. Мы называем это OP. (Где op это просто имя)

Добавьте ОП, чтобы уменьшить число. 15 + ОП = 15 + 5 = 20.

Снова добавьте OP к 20. 20 + ОП = 20 + 5 = 25.

Мы делаем это 2 раза, потому что мы должны вставить значения k-1.

Теперь повторите этот шаг для следующих двух соседних пикселей. Это показано в первой таблице.

После вставки значений необходимо отсортировать вставленные значения в порядке возрастания, чтобы между ними сохранялась симметрия.

Это показано во второй таблице

Таблица 1.

15	20	25	30	20	25	15
30	20	25	15	20	25	30

Таблица 2.

Мудрое масштабирование столбцов

Эта же процедура должна быть выполнена в колонке. Процедура включает в себя получение двух смежных значений пикселей, а затем вычитание меньшего из большего. Затем, после этого, вы должны разделить его на k. Сохраните результат как OP. Добавьте OP к меньшему, а затем снова добавьте OP к значению, которое приходит при первом добавлении OP. Вставьте новые значения.

Вот что ты получил после всего этого.

15	20	25	30	25	20	15
20	21	21	25	21	21	20
25	22	22	20	22	22	25
30	25	20	15	20	25	30

Новый размер изображения

Лучший способ вычислить формулу для размеров нового изображения — сравнить размеры исходного изображения и конечного изображения. Размеры исходного изображения были 2 х 3. А размеры нового изображения — 4 х 7.

Формула, таким образом, имеет вид:

(K (количество строк минус 1) + 1) X (K (количество строк минус 1) + 1)

Преимущества и недостатки

Одно из явных преимуществ алгоритма k-кратного масштабирования заключается в том, что он способен вычислять масштабирование любого фактора, который был мощью алгоритма репликации пикселей, а также он дает улучшенный результат (менее размытый), который был силой метода удержания нулевого порядка. Таким образом, следовательно, он включает в себя силу двух алгоритмов.

Единственная сложность этого алгоритма состоит в том, что он должен быть отсортирован в конце, что является дополнительным шагом и, таким образом, увеличивает стоимость вычислений.

Пространственное разрешение

Разрешение изображения

Разрешение изображения может быть определено многими способами. Один тип этого, который является разрешением пикселей, обсуждался в руководстве по разрешению пикселей и соотношению сторон.

В этом уроке мы собираемся определить другой тип разрешения — пространственное разрешение.

Пространственное разрешение:

Пространственное разрешение гласит, что четкость изображения не может быть определена разрешением в пикселях. Количество пикселей в изображении не имеет значения.

Пространственное разрешение может быть определено как

мельчайшая различимая деталь на изображении. (Цифровая обработка изображений — Гонсалес, Вудс — 2-е издание)

Или другим способом мы можем определить пространственное разрешение как количество независимых значений пикселей на дюйм.

Короче говоря, пространственное разрешение означает, что мы не можем сравнивать два разных типа изображений, чтобы увидеть, какой из них ясен, а какой нет. Если нам нужно сравнить два изображения, чтобы увидеть, какое из них более четкое или какое пространственное разрешение больше, мы должны сравнить два изображения одинакового размера.

Например:

Вы не можете сравнить эти два изображения, чтобы увидеть четкость изображения.

Хотя оба изображения одного и того же человека, но это не то условие, по которому мы судим. Изображение слева — увеличенное изображение Эйнштейна с размерами 227 x 222. Принимая во внимание, что изображение справа имеет размеры 980 X 749, а также это увеличенное изображение. Мы не можем сравнивать их, чтобы увидеть то, что более понятно. Помните, что коэффициент увеличения не имеет значения в этом состоянии, единственное, что имеет значение, это то, что эти два изображения не равны.

Таким образом, чтобы измерить пространственное разрешение, приведенные ниже изображения будут соответствовать цели.

Теперь вы можете сравнить эти две картинки. Оба изображения имеют одинаковые размеры 227 x 222. Теперь, сравнив их, вы увидите, что изображение с левой стороны имеет большее пространственное разрешение или оно более четкое, чем изображение с правой стороны. Это потому, что изображение справа — размытое изображение.

Измерение пространственного разрешения:

Поскольку пространственное разрешение относится к четкости, поэтому для разных устройств были приняты разные меры для его измерения.

Например:

• Точек на дюйм

• Линий на дюйм

• Пикселей на дюйм

Точек на дюйм

Линий на дюйм

Пикселей на дюйм

Они обсуждаются более подробно в следующем уроке, но ниже приведено лишь краткое введение.

Точек на дюйм:

Количество точек на дюйм или DPI обычно используется в мониторах.

Линий на дюйм:

Линии на дюйм или LPI обычно используются в лазерных принтерах.

Пиксель на дюйм:

Пиксель на дюйм или PPI измеряется для различных устройств, таких как планшеты, мобильные телефоны и т. Д.

Пиксели, точки и линии на дюйм

В предыдущем уроке о пространственном разрешении мы обсудили краткое введение PPI, DPI, LPI. Теперь мы официально собираемся обсудить все из них.

Пикселей на дюйм.

Плотность пикселей или пикселей на дюйм является мерой пространственного разрешения для различных устройств, включая планшеты, мобильные телефоны.

Чем выше ИЦП, тем выше качество. Для того, чтобы лучше понять это, вот как это рассчитано. Рассчитаем PPI мобильного телефона.

Расчет пикселей на дюйм (PPI) Samsung galaxy S4:

Samsung Galaxy S4 имеет PPI ​​или плотность пикселей 441. Но как он рассчитывается?

Прежде всего мы будем использовать теорему Пифагора для вычисления диагонального разрешения в пикселях.

Это может быть дано как:

Где a и b — разрешение по высоте и ширине в пикселях, а c — диагональное разрешение в пикселях.

Для Samsung Galaxy S4 это 1080 х 1920 пикселей.

Таким образом, помещение этих значений в уравнение дает результат

С = 2202,90717

Теперь посчитаем PPI

PPI = c / размер диагонали в дюймах

Размер диагонали в дюймах Samsun galaxy s4 составляет 5,0 дюйма, что можно подтвердить в любом месте.

PPI = 2202,90717 / 5,0

PPI = 440,58

PPI = 441 (приблизительно)

Это означает, что плотность пикселей Samsung Galaxy S4 составляет 441 PPI.

Точек на дюйм.

Dpi часто относятся к PPI, тогда как между этими двумя значениями есть разница. DPI или число точек на дюйм — это мера пространственного разрешения принтеров. В случае принтеров dpi означает, сколько точек чернил напечатано на дюйм, когда изображение распечатывается с принтера.

Помните, что необязательно, чтобы каждый пиксель на дюйм печатался одной точкой на дюйм. Может быть много точек на дюйм, используемых для печати одного пикселя. Причина этого в том, что большинство цветных принтеров использует модель CMYK. Цвета ограничены. Принтер должен выбрать один из этих цветов, чтобы сделать цвет пикселя, тогда как в ПК у вас есть сотни тысяч цветов.

Чем выше значение dpi принтера, тем выше качество напечатанного документа или изображения на бумаге.

Обычно некоторые лазерные принтеры имеют разрешение 300 точек на дюйм, а некоторые — 600 и более.

Линий на дюйм

Когда dpi относится к точкам на дюйм, лайнер на дюйм относится к линиям точек на дюйм. Разрешение полутонового экрана измеряется в строках на дюйм.

В следующей таблице приведены некоторые строки на дюйм емкости принтера.

принтер	LPI
Снимок экрана	45-65 lpi
Лазерный принтер (300 точек на дюйм)	65 lpi
Лазерный принтер (600 точек на дюйм)	85-105 lpi
Офсетная печать (газетная бумага)	85 lpi
Офсетная печать (мелованная бумага)	85-185 lpi

Разрешение уровня серого

Разрешение изображения:

Разрешение может быть определено как общее количество пикселей в изображении. Это обсуждалось в разрешении изображения. Мы также обсудили, что четкость изображения зависит не от количества пикселей, а от пространственного разрешения изображения. Это обсуждалось в пространственном разрешении. Здесь мы собираемся обсудить другой тип разрешения, который называется разрешением уровня серого.

Разрешение уровня серого:

Разрешение уровня серого относится к предсказуемому или детерминированному изменению оттенков или уровней серого на изображении.

Короче говоря, уровень разрешения серого равен числу бит на пиксель.

Мы уже обсуждали биты на пиксель в нашем уроке о битах на пиксель и требованиях к хранению изображений. Мы кратко определим здесь bpp.

BPP:

Количество различных цветов в изображении зависит от глубины цвета или битов на пиксель.

Математически:

Математическое соотношение, которое может быть установлено между разрешением уровня серого и битами на пиксель, может быть задано как.

В этом уравнении L относится к числу уровней серого. Его также можно определить как оттенки серого. И k относится к bpp или битам на пиксель. Таким образом, повышение 2 до мощности бит на пиксель равно разрешению уровня серого.

Например:

Приведенное выше изображение Эйнштейна представляет собой изображение в оттенках серого. Означает, что это изображение с 8 битами на пиксель или 8 бит на пиксель.

Теперь, если мы рассчитаем разрешение уровня серого, вот как мы это сделаем.

Это означает, что разрешение уровня серого составляет 256. Или иначе мы можем сказать, что это изображение имеет 256 различных оттенков серого.

Чем больше бит на пиксель изображения, тем больше разрешение уровня серого.

Определение разрешения уровня серого в терминах bpp:

Нет необходимости, чтобы разрешение уровня серого определялось только в терминах уровней. Мы также можем определить его в терминах бит на пиксель.

Например:

Если вам дается изображение 4 bpp, и вас просят вычислить его разрешение уровня серого. Есть два ответа на этот вопрос.

Первый ответ — 16 уровней.

Второй ответ — 4 бита.

Нахождение bpp из разрешения уровня серого:

Вы также можете найти биты на пиксели из заданного разрешения уровня серого. Для этого нам просто нужно немного скрутить формулу.

Уравнение 1.

Эта формула находит уровни. Теперь, если нам нужно найти биты на пиксель или в этом случае k, мы просто изменим это следующим образом.

K = логарифмическая основа 2 (L) Уравнение (2)

Потому что в первом уравнении соотношение между уровнями (L) и битами на пиксель (k) является экспоненциальным. Теперь мы должны вернуть его, и, таким образом, обратная экспонента равна log.

Давайте возьмем пример, чтобы найти биты на пиксель из разрешения уровня серого.

Например:

Если вам дано изображение 256 уровней. Какие биты на пиксель требуются для этого.

Положив 256 в уравнение, мы получим.

K = логарифмическая основа 2 (256)

К = 8.

Таким образом, ответ 8 бит на пиксель.

Разрешение и квантизация уровня серого:

Квантование будет официально введено в следующем уроке, но здесь мы просто собираемся объяснить связь между разрешением уровня серого и квантованием.

Разрешение уровня серого находится на оси Y сигнала. В учебном пособии Введение в сигналы и систему мы изучили, что оцифровка аналогового сигнала требует двух шагов. Выборка и квантование.

Отбор проб производится по оси х. И квантование выполняется по оси Y.

Таким образом, это означает, что оцифровка разрешения уровня серого изображения выполняется в квантовании.

Концепция квантования

Мы ввели квантование в нашем уроке сигналов и системы. Мы официально собираемся связать это с цифровыми изображениями в этом уроке. Давайте сначала немного поговорим о квантовании.

Оцифровка сигнала.

Как мы видели в предыдущих уроках, преобразование аналогового сигнала в цифровой требует двух основных шагов. Выборка и квантование. Отбор проб производится по оси х. Это преобразование оси x (бесконечные значения) в цифровые значения.

На рисунке ниже показана выборка сигнала.

Выборка по отношению к цифровым изображениям:

Концепция выборки напрямую связана с масштабированием. Чем больше образцов вы берете, тем больше пикселей вы получаете. Избыточную дискретизацию также можно назвать масштабированием. Это обсуждалось в учебнике по сэмплированию и масштабированию.

Но история оцифровки сигнала не заканчивается также на выборке, есть еще один шаг, который известен как Квантизация.

Что такое квантование.

Квантование противоположно выборке. Это сделано по оси Y. Когда вы квантизируете изображение, вы фактически делите сигнал на кванты (разделы).

На оси x сигнала находятся значения координат, а на оси y — амплитуды. Оцифровка амплитуд известна как квантование.

Вот как это делается

На этом изображении видно, что сигнал был количественно разделен на три разных уровня. Это означает, что когда мы производим выборку изображения, мы на самом деле собираем много значений, и при квантовании мы устанавливаем уровни для этих значений. Это может быть более ясно на изображении ниже.

На рисунке, показанном в выборке, хотя образцы были взяты, но они все еще охватывали вертикально непрерывный диапазон значений уровня серого. На рисунке, показанном выше, эти значения по вертикали были квантованы на 5 различных уровней или разделов. Начиная от 0 черных до 4 белых. Этот уровень может варьироваться в зависимости от типа изображения, которое вы хотите.

Связь квантования с уровнями серого была дополнительно обсуждена ниже.

Связь квантования с разрешением уровня серого:

Квантованная фигура, показанная выше, имеет 5 различных уровней серого. Это означает, что изображение, сформированное из этого сигнала, будет иметь только 5 разных цветов. Это было бы черно-белое изображение более или менее с некоторыми цветами серого. Теперь, если вы хотите улучшить качество изображения, есть одна вещь, которую вы можете сделать здесь. Что, чтобы увеличить уровни, или разрешение уровня серого вверх. Если вы увеличите этот уровень до 256, это означает, что у вас есть изображение в оттенках серого. Что гораздо лучше, чем простое черно-белое изображение.

Теперь 256, или 5 или любой другой уровень, который вы выбираете, называется уровнем серого. Запомните формулу, которую мы обсуждали в предыдущем уроке по разрешению уровня серого:

Мы обсуждали, что уровень серого можно определить двумя способами. Которые были эти двое.

• Уровень серого = количество бит на пиксель (BPP). (K в уравнении)

• Уровень серого = количество уровней на пиксель.

Уровень серого = количество бит на пиксель (BPP). (K в уравнении)

Уровень серого = количество уровней на пиксель.

В этом случае у нас уровень серого равен 256. Если нам нужно рассчитать количество бит, мы бы просто поместили значения в уравнение. В случае 256 уровней мы имеем 256 различных оттенков серого и 8 бит на пиксель, поэтому изображение будет изображением серой шкалы.

Уменьшение уровня серого

Теперь мы снизим уровни серого на изображении, чтобы увидеть эффект на изображении.

Например:

Допустим, у вас есть изображение 8bpp, которое имеет 256 различных уровней. Это изображение в градациях серого, и оно выглядит примерно так.

256 уровней серого

Теперь мы начнем снижать уровни серого. Сначала мы снизим уровни серого с 256 до 128.

128 уровней серого

После уменьшения уровня серого до половины, изображение не сильно влияет на изображение. Позволяет уменьшить еще немного.

64 уровня серого

По-прежнему не так много эффекта, тогда давайте уменьшать уровни больше.

32 уровня серого

Удивлен видеть, что все еще есть небольшой эффект. Может быть, это связано с тем, что это картина Эйнштейна, но позволяет еще больше снизить уровни.

16 уровней серого

Бум здесь, мы идем, изображение, наконец, показывает, что на него влияют уровни.

8 уровней серого

4 уровня серого

Теперь, прежде чем уменьшить его, еще на два уровня, вы можете легко увидеть, что изображение было сильно искажено, уменьшив уровни серого. Теперь мы снизим его до 2-х уровней, которые являются ничем иным, как простым черно-белым уровнем. Это означает, что изображение будет простым черно-белым изображением.

2 уровня серого

Это последний уровень, которого мы можем достичь, потому что если уменьшить его дальше, это будет просто черное изображение, которое не может быть интерпретировано.

Контурная:

Здесь есть интересное наблюдение: когда мы уменьшаем количество уровней серого, на изображении начинает появляться особый тип эффекта, который хорошо виден на рисунке с 16 уровнями серого. Этот эффект известен как контурное.

Кривые изо предпочтений:

Ответ на этот вопрос, почему он появляется, лежит в кривых изо предпочтений. Они обсуждаются в нашем следующем уроке Кривые контуров и предпочтений Iso.

Кривые предпочтений ISO

Что такое контур?

По мере того, как мы уменьшаем количество уровней серого в изображении, на нем начинают появляться некоторые ложные цвета или края. Это было показано в нашем последнем уроке квантования.

Давайте посмотрим на это.

Предположим, у нас есть изображение 8bpp (изображение в градациях серого) с 256 различными оттенками серого или уровнями серого.

Это изображение имеет 256 различных оттенков серого. Теперь, когда мы уменьшим его до 128 и еще больше уменьшим до 64, изображение будет более или менее таким же. Но когда мы уменьшаем его до 32 различных уровней, мы получаем такую ​​картину

Если вы посмотрите внимательно, вы обнаружите, что эффекты начинают появляться на изображении. Эти эффекты становятся более заметными, когда мы уменьшаем его до 16 уровней и получаем изображение, подобное этому.

Эти линии, которые начинают появляться на этом изображении, известны как контурные линии, которые очень хорошо видны на изображении выше.

Увеличение и уменьшение контуров

Эффект контурирования увеличивается при уменьшении количества уровней серого, а эффект уменьшается при увеличении количества уровней серого. Они оба наоборот

В.С.

Это означает, что большее квантование будет влиять на большее количество контуров и наоборот. Но так ли это всегда? Ответ — нет. Это зависит от чего-то еще, что обсуждается ниже.

Кривые изопреференции

Исследование было проведено на этот эффект уровня серого и контуров, и результаты были показаны на графике в виде кривых, известных как кривые предпочтения Iso.

Явление кривых Изопреференции показывает, что эффект контурирования зависит не только от уменьшения разрешения уровня серого, но и от детализации изображения.

Суть исследования заключается в:

Если изображение имеет больше деталей, эффект контуров начнет проявляться на этом изображении позже, по сравнению с изображением, которое имеет меньше деталей, когда уровни серого квантованы.

Согласно первоначальному исследованию, исследователи взяли эти три изображения, и они варьируют разрешение уровня серого во всех трех изображениях.

Изображения были

Уровень детализации:

Первое изображение имеет только лицо, и, следовательно, очень мало деталей. На втором изображении также есть некоторые другие объекты, такие как оператор, его камера, подставка для камеры, фоновые объекты и т. Д. В то время как третье изображение имеет больше деталей, чем все другие изображения.

Эксперимент:

Разрешение уровня серого было различным на всех изображениях, и аудитории было предложено субъективно оценить эти три изображения. После оценки был составлен график по результатам.

Результат:

Результат был нарисован на графике. Каждая кривая на графике представляет одно изображение. Значения на оси x представляют количество уровней серого, а значения на оси y представляют биты на пиксель (k).

График был показан ниже.

Согласно этому графику, мы можем видеть, что первое изображение, на котором было лицо, было контурировано раньше, чем все два других изображения. Второе изображение, которое было с оператором, было подвергнуто контуру немного после первого изображения, когда его уровни серого уменьшены. Это потому, что он имеет больше деталей, чем первое изображение. И третье изображение было подвергнуто контуру много после первых двух изображений, то есть: после 4 bpp. Это потому, что это изображение имеет больше деталей.

Заключение:

Таким образом, для более детальных изображений кривые изопреференции становятся все более и более вертикальными. Это также означает, что для изображения с большим количеством деталей требуется очень мало уровней серого.

Концепция дизеринга

В последних двух уроках квантования и контурной обработки мы видели, что уменьшение уровня серого на изображении уменьшает количество цветов, необходимых для обозначения изображения. Если уровни серого уменьшены на два 2, изображение, которое появляется, не имеет большого пространственного разрешения или не очень привлекательно.

Смешение:

Дизеринг — это процесс, посредством которого мы создаем иллюзии цвета, которых на самом деле нет. Это делается путем случайного расположения пикселей.

Например. Посмотрите на это изображение.

Это изображение только с черными и белыми пикселями. Его пиксели расположены в порядке, чтобы сформировать другое изображение, которое показано ниже. Обратите внимание, что расположение пикселей было изменено, но не количество пикселей.

Почему Дизеринг?

Зачем нам нужно дизеринг, ответ на этот вопрос заключается в его связи с квантованием.

Дизеринг с квантованием.

Когда мы выполняем квантование до последнего уровня, мы видим, что изображение, которое появляется на последнем уровне (уровень 2), выглядит следующим образом.

Теперь, как мы можем видеть из изображения здесь, эта картина не очень четкая, особенно если вы посмотрите на левую руку и заднюю часть изображения Эйнштейна. Также эта картина не имеет много информации или деталей Эйнштейна.

Теперь, если мы хотим изменить это изображение на какое-то изображение, которое дает больше деталей, чем это, мы должны выполнить дизеринг.

Выполнение дизеринга.

Прежде всего, мы будем работать над трёххолдингом. Размывание обычно работает, чтобы улучшить порог. Во время сшивания острые края появляются там, где градиенты сглажены на изображении.

В пороге мы просто выбираем постоянное значение. Все пиксели выше этого значения рассматриваются как 1, а все значения ниже него — как 0.

Мы получили это изображение после установления порога.

Поскольку в изображении не так много изменений, значения уже 0 и 1 или черно-белые изображения.

Теперь выполним случайное сглаживание. Это случайное расположение пикселей.

Мы получили изображение, которое дает меньше деталей, но его контраст очень низкий.

Таким образом, мы делаем еще больше размытия, которое увеличит контраст. Изображение, которое мы получили, это:

Теперь мы смешиваем понятия случайного смешения с порогом, и мы получили изображение, подобное этому.

Теперь вы видите, что мы получили все эти изображения, просто переставив пиксели изображения. Эта реорганизация может быть случайной или в соответствии с какой-то мерой.

Введение в гистограммы

Прежде чем обсуждать использование гистограмм при обработке изображений, мы сначала рассмотрим, что такое гистограмма, как она используется, а затем пример гистограмм, чтобы лучше понять гистограмму.

Гистограммы:

Гистограмма — это график. График, который показывает частоту чего-либо. Обычно гистограмма имеет столбцы, которые представляют частоту появления данных во всем наборе данных.

Гистограмма имеет две оси: ось x и ось y.

Ось X содержит событие, частоту которого вы должны посчитать.

Ось Y содержит частоту.

Разная высота столбца показывает разную частоту появления данных.

Обычно гистограмма выглядит следующим образом.

Теперь мы увидим пример этой гистограммы

Пример:

Рассмотрим класс студентов по программированию, и вы учите их питону.

В конце семестра вы получили такой результат, который показан в табл. Но это очень грязно и не показывает ваш общий результат в классе. Таким образом, вы должны составить гистограмму своего результата, показывающую общую частоту появления оценок в вашем классе. Вот как вы собираетесь это сделать.

Лист результатов:

название	класс
Джон
Джек	D
возчик	В
Томми
Лиза	C +
Дерек	A-
Том	B +

Гистограмма таблицы результатов:

Теперь, что вы собираетесь сделать, это то, что вы должны найти то, что происходит на осях х и у.

Есть одна вещь, чтобы быть уверенным, что ось Y содержит частоту, так что происходит на оси X. Ось X содержит событие, частота которого должна быть рассчитана. В этом случае ось х содержит оценки.

Теперь мы расскажем, как использовать гистограмму на изображении.

Гистограмма изображения

Гистограмма изображения, как и другие гистограммы, также показывает частоту. Но гистограмма изображения показывает частоту значений интенсивности пикселей. На гистограмме изображения ось x показывает интенсивности уровня серого, а ось y показывает частоту этих интенсивностей.

Например:

Гистограмма приведенной выше картины Эйнштейна будет примерно такой

Ось х гистограммы показывает диапазон значений пикселей. Поскольку это изображение размером 8 бит на дюйм, это означает, что в нем 256 уровней серого или оттенки серого. Вот почему диапазон оси x начинается с 0 и заканчивается на 255 с зазором 50. Тогда как на оси y есть счетчик этих интенсивностей.

Как видно из графика, большинство столбцов, которые имеют высокую частоту, находятся в первой половине, которая является более темной частью. Это означает, что изображение, которое мы получили, темнее. И это тоже можно доказать по изображению.

Применение гистограмм:

Гистограмма имеет много применений в обработке изображений. Первое использование, как это также обсуждалось выше, — это анализ изображения. Мы можем предсказать изображение, просто посмотрев на его гистограмму. Это как смотреть рентгеновский снимок кости тела.

Второе использование гистограммы для целей яркости. Гистограмма имеет широкое применение в яркости изображения. Не только яркость, но и гистограммы также используются для настройки контрастности изображения.

Другое важное использование гистограммы — выравнивание изображения.

И последнее, но не менее важное, гистограмма широко используется в пороговых значениях. Это в основном используется в компьютерном зрении.

Яркость и контрастность

Яркость:

Яркость это относительный термин. Это зависит от вашего зрительного восприятия. Поскольку яркость является относительным термином, яркость можно определить как количество энергии, излучаемой источником света относительно источника, с которым мы сравниваем его. В некоторых случаях мы можем легко сказать, что изображение яркое, а в некоторых случаях его нелегко воспринимать.

Например:

Just have a look at both of these images , and compare which one is brighter.

We can easily see , that the image on the right side is brighter as compared to the image on the left.

But if the image on the right is made more darker then the first one , then we can say that the image on the left is more brighter then the left.

Как сделать изображение ярче.

Яркость можно просто увеличить или уменьшить простым сложением или вычитанием матрицы изображения.

Рассмотрим это черное изображение из 5 строк и 5 столбцов

Поскольку мы уже знаем, что каждое изображение имеет матрицу позади, которая содержит значения пикселей. Эта матрица изображений приведена ниже.

0	0	0	0	0
0	0	0	0	0
0	0	0	0	0
0	0	0	0	0
0	0	0	0	0

Так как вся матрица заполнена нулями, а изображение очень сильно темнее.

Теперь мы сравним его с другим таким же черным изображением, чтобы увидеть, стало ли это изображение ярче или нет.

Тем не менее, оба изображения одинаковы, теперь мы выполним некоторые операции над изображением1, благодаря чему оно станет ярче второго.

What we will do is , that we will simply add a value of 1 to each of the matrix value of image 1. After adding the image 1 would something like this.

Now we will again compare it with image 2 , and see any difference.

Мы видим, что мы все еще не можем сказать, какое изображение ярче, поскольку оба изображения выглядят одинаково.

Now what we will do , is that we will add 50 to each of the matrix value of the image 1 and see what the image has become.

Вывод приведен ниже.

Now again , we will compare it with image 2.

Now you can see that the image 1 is slightly brighter then the image 2. We go on , and add another 45 value to its matrix of image 1 , and this time we compare again both images.

Now when you compare it , you can see that this image1 is clearly brighter then the image 2.

Даже оно ярче старого изображения1. At this point the matrix of the image1 contains 100 at each index as first add 5 , then 50 , then 45. So 5 + 50 + 45 = 100.

контрастировать

Контраст можно просто объяснить как разницу между максимальной и минимальной интенсивностью пикселей в изображении.

Например.

Рассмотрим окончательное изображение1 по яркости.

Матрица этого изображения:

100	100	100	100	100
100	100	100	100	100
100	100	100	100	100
100	100	100	100	100
100	100	100	100	100

Максимальное значение в этой матрице составляет 100.

Минимальное значение в этой матрице составляет 100.

Контраст = максимальная интенсивность пикселей (вычитается из) минимальной интенсивности пикселей

= 100 (вычтено) 100

= 0

0 означает, что это изображение имеет 0 контраст.

Преобразования изображения

Прежде чем мы обсудим, что такое преобразование изображения, мы обсудим, что такое преобразование.

Transformation.

Преобразование является функцией. Функция, которая отображает один набор в другой после выполнения некоторых операций.

Digital Image Processing system:

We have already seen in the introductory tutorials that in digital image processing , we will develop a system that whose input would be an image and output would be an image too. И система выполнит некоторую обработку входного изображения и выдаст его в виде обработанного изображения. Это показано ниже.

Теперь функция, применяемая внутри этой цифровой системы, которая обрабатывает изображение и конвертирует его в вывод, может называться функцией преобразования.

As it shows transformation or relation , that how an image1 is converted to image2.

Image transformation.

Рассмотрим это уравнение

G (x, y) = T {f (x, y)}

In this equation ,

F (x, y) = входное изображение, к которому должна быть применена функция преобразования.

G (x, y) = выходное изображение или обработанное изображение.

Т — функция преобразования.

Эта связь между входным изображением и обработанным выходным изображением также может быть представлена ​​как.

s = T (r)

где r на самом деле значение пикселя или интенсивность уровня серого f (x, y) в любой точке. И s — это значение пикселя или интенсивность уровня серого g (x, y) в любой точке.

Базовое преобразование уровня серого было обсуждено в нашем уроке базовых преобразований уровня серого.

Теперь мы собираемся обсудить некоторые из самых основных функций преобразования.

Примеры:

Рассмотрим эту функцию преобразования.

Lets take the point r to be 256, and the point p to be 127. Consider this image to be a one bpp image. Это означает, что у нас есть только два уровня интенсивностей, которые равны 0 и 1. Таким образом, в этом случае преобразование, показанное графиком, можно объяснить как.

All the pixel intensity values that are below 127 (point p) are 0 , means black. And all the pixel intensity values that are greater then 127, are 1 , that means white. But at the exact point of 127, there is a sudden change in transmission, so we cannot tell that at that exact point , the value would be 0 or 1.

Математически эта функция преобразования может быть обозначена как:

Consider another transformation like this:

Now if you will look at this particular graph , you will see a straight transition line between input image and output image.

Это показывает, что для каждого пикселя или значения интенсивности входного изображения существует одинаковое значение интенсивности выходного изображения. Это означает, что выходное изображение является точной копией входного изображения.

Это может быть математически представлено как:

g (x, y) = f (x, y)

входное и выходное изображение в этом случае показано ниже.

Скольжение гистограммы

Основная концепция гистограмм обсуждалась в учебном пособии Введение в гистограммы. Но мы кратко представим здесь гистограмму.

Histogram:

Гистограмма — это не что иное, как график, который показывает частоту появления данных. Гистограммы широко используются в обработке изображений, из которых мы собираемся обсудить здесь одного пользователя, который называется скольжением гистограммы.

Histogram sliding.

In histogram sliding , we just simply shift a complete histogram rightwards or leftwards. Due to shifting or sliding of histogram towards right or left , a clear change can be seen in the image.In this tutorial we are going to use histogram sliding for manipulating brightness.

Термин, т. Е. Яркость, обсуждался в нашем уроке введения в яркость и контраст. Но мы собираемся кратко определить здесь.

Яркость:

Яркость это относительный термин. Яркость можно определить как интенсивность света, излучаемого конкретным источником света.

Контраст:

Контрастность может быть определена как разница между максимальной и минимальной интенсивностью пикселей в изображении.

Скользящие гистограммы

Увеличение яркости с помощью скольжения гистограммы

Гистограмма этого изображения показана ниже.

На оси Y этой гистограммы находятся частота или счетчик. And on the x axis , we have gray level values. As you can see from the above histogram , that those gray level intensities whose count is more then 700, lies in the first half portion, means towards blacker portion. Вот почему мы получили изображение, которое немного темнее.

In order to bright it, we will slide its histogram towards right , or towards whiter portion. Для этого нам нужно добавить как минимум значение 50 к этому изображению. Because we can see from the histogram above , that this image also has 0 pixel intensities , that are pure black. So if we add 0 to 50 , we will shift all the values lies at 0 intensity to 50 intensity and all the rest of the values will be shifted accordingly.

Давай сделаем это.

Вот что мы получили после добавления 50 к интенсивности каждого пикселя.

Изображение было показано ниже.

И его гистограмма была показана ниже.

Давайте сравним эти два изображения и их гистограммы, чтобы увидеть, какие изменения нужно получить.

Заключение:

Как видно из новой гистограммы, все значения пикселей смещены вправо, и их эффект виден на новом изображении.

Уменьшение яркости с помощью скольжения гистограммы

Now if we were to decrease brightness of this new image to such an extent that the old image look brighter , we got to subtract some value from all the matrix of the new image. The value which we are going to subtract is 80. Because we already add 50 to the original image and we got a new brighter image, now if we want to make it darker , we have to subtract at least more than 50 from it.

И это то, что мы получили после вычитания 80 из нового изображения.

Заключение:

It is clear from the histogram of the new image , that all the pixel values has been shifted towards right and thus , it can be validated from the image that new image is darker and now the original image look brighter as compare to this new image.

Растяжение гистограммы

Еще одно преимущество гистограмм, которое мы обсуждали в нашем уроке введения в гистограммы, — это усиление контраста.

Есть два метода усиления контраста. Первый называется растяжением гистограммы, увеличивающим контраст. Второй называется выравниванием гистограммы, которое усиливает контраст, и это обсуждалось в нашем уроке выравнивания гистограммы.

Before we will discuss the histogram stretching to increase contrast , we will briefly define contrast.

Contrast.

Контрастность — это разница между максимальной и минимальной интенсивностью пикселей.

Посмотрите на это изображение.

Гистограмма этого изображения показана ниже.

Теперь мы рассчитываем контраст по этому изображению.

Контрастность = 225

Теперь мы увеличим контраст изображения.

Increasing the contrast of the image:

Формула растяжения гистограммы изображения для увеличения контрастности

Формула требует нахождения минимальной и максимальной интенсивности пикселей, умноженной на уровни серого. В нашем случае изображение 8bpp, поэтому уровни серого 256.

Минимальное значение равно 0, а максимальное — 225. Таким образом, формула в нашем случае

где f (x, y) обозначает значение интенсивности каждого пикселя. Для каждого f (x, y) в изображении мы рассчитаем эту формулу.

После этого мы сможем усилить контраст.

Следующее изображение появляется после применения растяжения гистограммы.

Растянутая гистограмма этого изображения показана ниже.

Обратите внимание на форму и симметрию гистограммы. Гистограмма теперь растягивается или другими способами расширяется. Посмотри на это.

В этом случае контраст изображения можно рассчитать как

Контраст = 240

Отсюда можно сказать, что контрастность изображения увеличивается.

Note: this method of increasing contrast doesnot work always, but it fails on some cases.

Отсутствие растяжения гистограммы

Как мы уже говорили, этот алгоритм в некоторых случаях дает сбой. Эти случаи включают в себя изображения с интенсивностью пикселей 0 и 255 присутствуют на изображении

Because when pixel intensities 0 and 255 are present in an image , then in that case they become the minimum and maximum pixel intensity which ruins the formula like this.

Оригинальная Формула

Помещение значений регистра в формулу:

Упростите это выражение

Это означает, что выходное изображение равно обработанному изображению. Это означает, что эффект растяжения гистограммы на этом изображении отсутствует.

Введение в вероятность

PMF и CDF оба термина относятся к вероятности и статистике. Now the question that should arise in your mind , is that why are we studying probability. Это потому, что эти две концепции PMF и CDF будут использоваться в следующем уроке по выравниванию гистограммы. So if you dont know how to calculate PMF and CDF , you can not apply histogram equalization on your image

,

Что такое PMF?

PMF обозначает функцию вероятности массы. As it name suggest , it gives the probability of each number in the data set or you can say that it basically gives the count or frequency of each element.

How PMF is calculated:

Мы рассчитаем PMF двумя разными способами. First from a matrix , because in the next tutorial , we have to calculate the PMF from a matrix , and an image is nothing more then a two dimensional matrix.

Затем мы возьмем другой пример, в котором мы будем вычислять PMF по гистограмме.

Рассмотрим эту матрицу.

1	2	7	5	6
7	2	3	4	5
0	1	5	7	3
1	2	5	6	7
6	1	0	3	4

Now if we were to calculate the PMF of this matrix , here how we are going to do it.

At first , we will take the first value in the matrix , and then we will count , how much time this value appears in the whole matrix. After count they can either be represented in a histogram , or in a table like this below.

PMF

0	2	2/25
1	4	4/25
2	3	3/25
3	3	3/25
4	2	2/25
5	4	4/25
6	3	3/25
7	4	4/25

Обратите внимание, что сумма счета должна быть равна общему количеству значений.

Расчет PMF по гистограмме

Вышеупомянутая гистограмма показывает частоту значений уровня серого для 8 бит на пиксельное изображение.

Now if we have to calculate its PMF , we will simple look at the count of each bar from vertical axis and then divide it by total count.

Таким образом, PMF приведенной выше гистограммы таков.

Еще одна важная вещь, которую следует отметить в приведенной выше гистограмме, это то, что она не монотонно увеличивается. Поэтому, чтобы увеличить его монотонно, мы рассчитаем его CDF.

Что такое CDF?

CDF обозначает совокупную распределительную функцию. Это функция, которая вычисляет совокупную сумму всех значений, которые рассчитываются с помощью PMF. Это в основном подводит итог предыдущего.

Как рассчитывается?

Мы рассчитаем CDF, используя гистограмму. Вот как это делается. Рассмотрим гистограмму, показанную выше, которая показывает PMF.

Since this histogram is not increasing monotonically , so will make it grow monotonically.

We will simply keep the first value as it is , and then in the 2nd value , we will add the first one and so on.

Вот CDF вышеупомянутой функции PMF.

Now as you can see from the graph above , that the first value of PMF remain as it is. Второе значение PMF добавляется в первое значение и помещается более 128. Третье значение PMF добавляется во второе значение CDF, что дает 110/110, что равно 1.

And also now , the function is growing monotonically which is necessary condition for histogram equalization.

Использование PMF и CDF при выравнивании гистограммы

Histogram equalization.

Выравнивание гистограммы обсуждается в следующем уроке, но краткое введение в выравнивание гистограммы приведено ниже.

Выравнивание гистограммы используется для повышения контрастности изображений.

PMF и CDF оба используются в выравнивании гистограммы, как описано в начале этого урока. In the histogram equalization , the first and the second step are PMF and CDF. Since in histogram equalization , we have to equalize all the pixel values of an image. Таким образом, PMF помогает нам вычислить вероятность каждого значения пикселя в изображении. И CDF дает нам совокупную сумму этих значений. Further on , this CDF is multiplied by levels , to find the new pixel intensities , which are mapped into old values , and your histogram is equalized.

Histogram Equalization

We have already seen that contrast can be increased using histogram stretching. In this tutorial we will see that how histogram equalization can be used to enhance contrast.

Before performing histogram equalization, you must know two important concepts used in equalizing histograms. These two concepts are known as PMF and CDF.

They are discussed in our tutorial of PMF and CDF. Please visit them in order to successfully grasp the concept of histogram equalization.

Histogram Equalization:

Histogram equalization is used to enhance contrast. It is not necessary that contrast will always be increase in this. There may be some cases were histogram equalization can be worse. In that cases the contrast is decreased.

Lets start histogram equalization by taking this image below as a simple image.

Образ

Histogram of this image:

The histogram of this image has been shown below.

Now we will perform histogram equalization to it.

PMF:

First we have to calculate the PMF (probability mass function) of all the pixels in this image. If you donot know how to calculate PMF, please visit our tutorial of PMF calculation.

CDF:

Our next step involves calculation of CDF (cumulative distributive function). Again if you donot know how to calculate CDF , please visit our tutorial of CDF calculation.

Calculate CDF according to gray levels

Lets for instance consider this , that the CDF calculated in the second step looks like this.

Gray Level Value	CDF
0	0,11
1	0,22
2	0,55
3	0,66
4	0,77
5	0,88
6	0,99
7	1

Then in this step you will multiply the CDF value with (Gray levels (minus) 1) .

Considering we have an 3 bpp image. Then number of levels we have are 8. And 1 subtracts 8 is 7. So we multiply CDF by 7. Here what we got after multiplying.

Gray Level Value	CDF	CDF * (Levels-1)
0	0,11	0
1	0,22	1
2	0,55	3
3	0,66	4
4	0,77	5
5	0,88	6
6	0,99	6
7	1	7

Now we have is the last step , in which we have to map the new gray level values into number of pixels.

Lets assume our old gray levels values has these number of pixels.

Gray Level Value	частота
0	2
1	4
2	6
3	8
4	10
5	12
6	14
7	16

---

Now if we map our new values to , then this is what we got.

Gray Level Value	New Gray Level Value	частота
0	0	2
1	1	4
2	3	6
3	4	8
4	5	10
5	6	12
6	6	14
7	7	16

---

Now map these new values you are onto histogram , and you are done.

Lets apply this technique to our original image. After applying we got the following image and its following histogram.

Histogram Equalization Image

Cumulative Distributive function of this image

Histogram Equalization histogram

Comparing both the histograms and images

Заключение

As you can clearly see from the images that the new image contrast has been enhanced and its histogram has also been equalized. There is also one important thing to be note here that during histogram equalization the overall shape of the histogram changes, where as in histogram stretching the overall shape of histogram remains same.

Преобразование уровня серого

Мы обсудили некоторые из основных преобразований в нашем уроке Основы преобразования. В этом уроке мы рассмотрим некоторые основные преобразования уровня серого.

Улучшение изображения

Улучшение изображения обеспечивает лучшую контрастность и более детальное изображение по сравнению с не улучшенным изображением. Улучшение изображения имеет очень много применений. It is used to enhance medical images , images captured in remote sensing , images from satellite etc

Функция преобразования была дана ниже

s = T (r)

где r — пиксели входного изображения, а s — пиксели выходного изображения. T является функцией преобразования, которая отображает каждое значение r на каждое значение s. Улучшение изображения может быть сделано с помощью преобразований уровня серого, которые обсуждаются ниже.

Преобразование уровня серого

Существует три основных преобразования уровня серого.

• линейный

• логарифмический

• Сила закона

линейный

логарифмический

Сила закона

Общий график этих переходов показан ниже.

Линейное преобразование

Сначала мы рассмотрим линейное преобразование. Линейное преобразование включает в себя простую идентичность и отрицательное преобразование. Преобразование идентичности обсуждалось в нашем руководстве по преобразованию изображения, но здесь дано краткое описание этого преобразования.

Переход идентичности показан прямой линией. При этом переходе каждое значение входного изображения напрямую отображается на каждое значение выходного изображения. Это приводит к тому же входному изображению и выходному изображению. И, следовательно, называется преобразованием личности. It has been shown below

Негативное преобразование

Второе линейное преобразование — это отрицательное преобразование, которое инвертирует преобразование идентичности. При отрицательном преобразовании каждое значение входного изображения вычитается из L-1 и отображается на выходное изображение.

Результат примерно такой.

Входное изображение

Выходное изображение

В этом случае был выполнен следующий переход.

s = (L — 1) — r

since the input image of Einstein is an 8 bpp image , so the number of levels in this image are 256. Putting 256 in the equation, we get this

с = 255 — г

Таким образом, каждое значение вычитается на 255, и результирующее изображение было показано выше. So what happens is that , the lighter pixels become dark and the darker picture becomes light. И это приводит к негативному изображению.

Это было показано на графике ниже.

Logarithmic transformations:

Логарифмическое преобразование дополнительно содержит два типа преобразования. Преобразование журнала и обратное преобразование журнала.

Преобразование журнала

Лог преобразования могут быть определены по этой формуле

s = c log (r + 1).

Где s и r — это значения пикселей на выходе и входном изображении, а c — это константа. Значение 1 добавляется к каждому значению пикселя входного изображения, потому что если в изображении присутствует интенсивность пикселей 0, тогда log (0) равен бесконечности. So 1 is added , to make the minimum value at least 1.

During log transformation , the dark pixels in an image are expanded as compare to the higher pixel values. Более высокие значения пикселей отчасти сжаты в преобразовании журнала. Это приводит к следующему улучшению изображения.

Значение c в преобразовании журнала корректирует вид улучшения, которое вы ищете.

Входное изображение

Log Tranform Image

Обратное лог-преобразование противоположно лог-преобразованию.

Власть — Закон преобразований

Есть еще две трансформации — степенные преобразования, которые включают n-ю степень и n-ную корневую трансформацию. Эти преобразования могут быть заданы выражением:

s = сг ^ γ

Этот символ γ называется гаммой, благодаря чему это преобразование также известно как гамма-преобразование.

Изменение значения γ влияет на улучшение изображений. Различные устройства отображения / мониторы имеют собственную гамма-коррекцию, поэтому они отображают свое изображение с различной интенсивностью.

Этот тип преобразования используется для улучшения изображений для различных типов устройств отображения. Гамма разных устройств отображения отличается. For example Gamma of CRT lies in between of 1.8 to 2.5 , that means the image displayed on CRT is dark.

Корректирующая гамма.

s = сг ^ γ

s = сг ^ (1 / 2.5)

Здесь показано то же изображение, но с разными значениями гаммы.

Например:

Гамма = 10

Гамма = 8

Гамма = 6

Концепция свертки

Этот урок об одной из очень важных концепций сигналов и системы. Мы будем полностью обсуждать свертку. Что это? Почему это? Что мы можем достичь с этим?

Мы начнем обсуждать свертку с основ обработки изображений.

What is image processing.

Как мы уже обсуждали во введении к учебным пособиям по обработке изображений, а также в сигнале и системе, эта обработка изображения является более или менее изучением сигналов и систем, потому что изображение — это не что иное, как двумерный сигнал.

Also we have discussed , that in image processing , we are developing a system whose input is an image and output would be an image. Это наглядно представлено как.

Поле, показанное на приведенном выше рисунке и помеченное как «Система цифровой обработки изображений», можно рассматривать как черный ящик.

Это может быть лучше представлено как:

Куда мы дошли до сих пор

До сих пор мы обсуждали два важных метода манипулирования изображениями. Или, другими словами, мы можем сказать, что наш черный ящик до сих пор работает двумя разными способами.

Два разных способа манипулирования изображениями были

Graphs (Histograms)

Этот метод известен как обработка гистограммы. We have discussed it in detail in previous tutorials for increase contrast , image enhancement , brightness etc

Transformation functions

This method is known as transformations , in which we discussed different type of transformations and some gray level transformations

Еще один способ работы с изображениями

Здесь мы собираемся обсудить другой метод работы с изображениями. Этот другой метод известен как свертка. Обычно черный ящик (система), используемый для обработки изображений, представляет собой систему LTI или систему, не зависящую от линейного времени. Под линейной мы подразумеваем такую ​​систему, в которой выход всегда линейный, ни лог, ни показатель, ни какая-либо другая. Под инвариантом времени мы понимаем систему, которая остается неизменной во времени.

Итак, теперь мы собираемся использовать этот третий метод. Это можно представить как.

Это может быть математически представлено как два способа

g (x, y) = h (x, y) * f (x, y)

Это можно объяснить как «маска, свернутая с изображением».

Или же

g (x, y) = f (x, y) * h (x, y)

Это можно объяснить как «изображение, свернутое с маской».

Есть два способа представить это, потому что оператор свертки (*) является коммутативным. H (x, y) — маска или фильтр.

Что такое маска?

Маска тоже сигнал. Он может быть представлен двумерной матрицей. The mask is usually of the order of 1×1, 3×3, 5×5 , 7×7 . A mask should always be in odd number , because other wise you cannot find the mid of the mask. Почему мы должны найти середину маски. The answer lies below, in topic of , how to perform convolution?

Как выполнить свертку?

In order to perform convolution on an image , following steps should be taken.

• Переверните маску (по горизонтали и вертикали) только один раз

• Наденьте маску на изображение.

• Умножьте соответствующие элементы и затем добавьте их

• Повторяйте эту процедуру, пока все значения изображения не будут рассчитаны.

Переверните маску (по горизонтали и вертикали) только один раз

Наденьте маску на изображение.

Умножьте соответствующие элементы и затем добавьте их

Повторяйте эту процедуру, пока все значения изображения не будут рассчитаны.

Пример свертки

Давайте выполним некоторую свертку. Шаг 1 — перевернуть маску.

Маска:

Давайте возьмем нашу маску, чтобы быть этим.

1	2	3
4	5	6
7	8	9

Перевернуть маску по горизонтали

3	2	1
6	5	4
9	8	7

Перевернуть маску по вертикали

9	8	7
6	5	4
3	2	1

Образ:

Давайте рассмотрим изображение так

2	4	6
8	10	12
14	16	18

свертка

Свертывающая маска над изображением. Это сделано таким образом. Поместите центр маски на каждый элемент изображения. Умножьте соответствующие элементы, а затем добавьте их и вставьте результат в элемент изображения, на который вы помещаете центр маски.

The box in red color is the mask , and the values in the orange are the values of the mask. Черная цветная рамка и значения принадлежат изображению. Now for the first pixel of the image , the value will be calculated as

Первый пиксель = (5 * 2) + (4 * 4) + (2 * 8) + (1 * 10)

= 10 + 16 + 16 + 10

= 52

Поместите 52 в исходное изображение в первый индекс и повторите эту процедуру для каждого пикселя изображения.

Почему свертка

Свертка может достичь чего-то, чего не могут достичь два предыдущих метода манипулирования изображениями. Those include the blurring , sharpening , edge detection , noise reduction etc

Концепция Маски

What is a mask.

Маска — это фильтр. Концепция маскировки также известна как пространственная фильтрация. Маскировка также известна как фильтрация. В этой концепции мы имеем дело только с операцией фильтрации, которая выполняется непосредственно над изображением.

Пример маски показан ниже

-1	0	1
-1	0	1
-1	0	1

What is filtering.

Процесс фильтрации также известен как свертывание маски с изображением. Поскольку этот процесс аналогичен свертке, маски фильтра также известны как маски свертки.

How it is done.

Общий процесс фильтрации и применения масок состоит в перемещении маски фильтра от точки к точке на изображении. В каждой точке (x, y) исходного изображения отклик фильтра вычисляется по заранее определенной зависимости. Все значения фильтров предварительно определены и являются стандартными.

Типы фильтров

Обычно существует два типа фильтров. Один называется линейными фильтрами или сглаживающими фильтрами, а другие называются фильтрами частотной области.

Почему используются фильтры?

Фильтры применяются к изображению для нескольких целей. Два наиболее распространенных использования следующие:

• Фильтры используются для размывания и снижения шума

• Фильтры используются или обнаружение края и резкость

Фильтры используются для размывания и снижения шума

Фильтры используются или обнаружение края и резкость

Blurring and noise reduction:

Фильтры чаще всего используются для размытия и уменьшения шума. Размытие используется на этапах предварительной обработки, таких как удаление мелких деталей с изображения перед извлечением крупных объектов.

Masks for blurring.

Общие маски для размытия:

• Коробочный фильтр

• Средневзвешенный фильтр

Коробочный фильтр

Средневзвешенный фильтр

В процессе размытия мы уменьшаем содержание краев в изображении и пытаемся сделать переходы между различными интенсивностями пикселей как можно более плавными.

Уменьшение шума также возможно с помощью размытия.

Edge Detection and sharpness:

Маски или фильтры также можно использовать для обнаружения краев на изображении и для повышения резкости изображения.

What are edges.

Можно также сказать, что внезапные изменения разрывов в изображении называются ребрами. Значительные переходы в изображении называются краями. Изображение с краями показано ниже.

Original picture.

Та же картина с краями

Концепция размытия

Краткое введение в размытие было обсуждено в нашем предыдущем уроке концепции масок, но мы формально обсудим это здесь.

нечеткость

In blurring , we simple blur an image. Изображение выглядит более четким или более детальным, если мы можем правильно воспринимать в нем все объекты и их формы. Например. An image with a face, looks clear when we are able to identify eyes , ears , nose , lips , forehead etc very clear. Эта форма объекта обусловлена ​​его краями. So in blurring , we simple reduce the edge content and makes the transition form one color to the other very smooth.

Blurring vs zooming.

Возможно, вы видели размытое изображение при увеличении изображения. When you zoom an image using pixel replication , and zooming factor is increased, you saw a blurred image. This image also has less details , but it is not true blurring.

Because in zooming , you add new pixels to an image , that increase the overall number of pixels in an image , whereas in blurring , the number of pixels of a normal image and a blurred image remains the same.

Common example of a blurred image.

Types of filters.

Размытие может быть достигнуто многими способами. Общий тип фильтров, которые используются для выполнения размытия:

• Средний фильтр

• Средневзвешенный фильтр

• Гауссов фильтр

Средний фильтр

Средневзвешенный фильтр

Гауссов фильтр

Out of these three , we are going to discuss the first two here and Gaussian will be discussed later on in the upcoming tutorials.

Mean filter.

Средний фильтр также известен как фильтр Бокса и средний фильтр. Средний фильтр имеет следующие свойства.

• Должно быть странным образом

• Сумма всех элементов должна быть 1

• Все элементы должны быть одинаковыми

Должно быть странным образом

Сумма всех элементов должна быть 1

Все элементы должны быть одинаковыми

If we follow this rule , then for a mask of 3×3. Мы получаем следующий результат.

1/9	1/9	1/9
1/9	1/9	1/9
1/9	1/9	1/9

Поскольку это маска 3х3, это означает, что в ней 9 ячеек. Условие, что вся сумма элемента должна быть равна 1, может быть достигнуто путем деления каждого значения на 9. Как

1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 = 9/9 = 1

The result of a mask of 3×3 on an image is shown below.

Исходное изображение:

Размытое изображение

Может быть, результаты не очень ясны. Давайте увеличим размытие. Размытие можно увеличить, увеличив размер маски. The more is the size of the mask , the more is the blurring. Because with greater mask , greater number of pixels are catered and one smooth transition is defined.

The result of a mask of 5×5 on an image is shown below.

Исходное изображение:

Blurred Image:

Same way if we increase the mask , the blurring would be more and the results are shown below.

Результат маски 7х7 на изображении показан ниже.

Исходное изображение:

Blurred Image:

Результат маски 9×9 на изображении показан ниже.

Исходное изображение:

Blurred Image:

Результат маски 11×11 на изображении показан ниже.

Исходное изображение:

Blurred Image:

Weighted average filter.

В средневзвешенном фильтре мы придавали больший вес значению центра. За счет чего вклад центра становится больше остальных значений. Due to weighted average filtering , we can actually control the blurring.

Свойства взвешенного среднего фильтра.

• Должно быть странным образом

• Сумма всех элементов должна быть 1

• Вес центрального элемента должен быть больше, чем у всех остальных элементов.

Должно быть странным образом

Сумма всех элементов должна быть 1

Вес центрального элемента должен быть больше, чем у всех остальных элементов.

Фильтр 1

1	1	1
1	2	1
1	1	1

Выполняются два свойства (1 и 3). Но свойство 2 не выполняется. Таким образом, чтобы удовлетворить это, мы просто разделим весь фильтр на 10 или умножим его на 1/10.

Фильтр 2

1	1	1
1	10	1
1	1	1

Коэффициент деления = 18.

Концепция обнаружения краев

Мы кратко обсудили обнаружение краев в нашем уроке введения в маски. Мы официально обсудим обнаружение краев здесь.

Каковы края.

Можно также сказать, что внезапные изменения разрывов в изображении называются ребрами. Значимые переходы в изображении называются ребрами.

Типы ребер.

В целом ребра бывают трех типов:

• Горизонтальные края

• Вертикальные края

• Диагональные края

Горизонтальные края

Вертикальные края

Диагональные края

Зачем обнаруживать края.

Большая часть информации о форме изображения заключена в края. Итак, сначала мы обнаруживаем эти края на изображении и, используя эти фильтры, а затем, улучшая те области изображения, которые содержат края, резкость изображения будет увеличиваться, и изображение станет более четким.

Вот некоторые маски для обнаружения краев, которые мы обсудим в следующих уроках.

• Prewitt Operator

• Собел Оператор

• Робинсон Компас Маски

• Криш Компас Маски

• Лапласский оператор.

Prewitt Operator

Собел Оператор

Робинсон Компас Маски

Криш Компас Маски

Лапласский оператор.

Вышеупомянутые все фильтры являются линейными фильтрами или сглаживающими фильтрами.

Prewitt Operator

Оператор Prewitt используется для обнаружения краев по горизонтали и вертикали.

Собел Оператор

Оператор sobel очень похож на оператор Prewitt. Это также производная маска, которая используется для обнаружения краев. Он также рассчитывает края как в горизонтальном, так и в вертикальном направлении.

Робинсон Компас Маски

Этот оператор также известен как маска направления. В этом операторе мы берем одну маску и поворачиваем ее во всех 8 основных направлениях компаса, чтобы вычислить ребра каждого направления.

Кирш Компас Маски

Kirsch Compass Mask также является производной маской, которая используется для нахождения ребер. Маска Кирша также используется для расчета краев во всех направлениях.

Лапласский оператор.

Оператор Лапласа также является производным оператором, который используется для поиска ребер в изображении. Лапласиан является производной маской второго порядка. Это может быть далее разделено на положительный лапласиан и отрицательный лапласиан.

Все эти маски находят края. Некоторые находят горизонтально и вертикально, некоторые находят только в одном направлении, а некоторые находят во всех направлениях. Следующая концепция, которая следует за этим, является резкостью, которая может быть сделана, как только края извлечены из изображения

Заточка:

Резкость противоположна размытию. При размытии мы уменьшаем содержимое края, а в sharpneng мы увеличиваем содержимое края. Таким образом, чтобы увеличить содержание ребер в изображении, мы должны сначала найти ребра.

Края могут быть найдены любым из методов, описанных выше, с использованием любого оператора. После нахождения ребер мы добавим эти ребра на изображение, и, таким образом, у изображения будет больше краев, и оно будет выглядеть более резким.

Это один из способов повышения резкости изображения.

Резкое изображение показано ниже.

Исходное изображение

Резкость изображения

Prewitt Operator

Оператор Prewitt используется для обнаружения краев на изображении. Он обнаруживает два типа ребер:

• Горизонтальные края

• Вертикальные края

Горизонтальные края

Вертикальные края

Края рассчитываются с использованием разности между соответствующими интенсивностями пикселей изображения. Все маски, которые используются для обнаружения краев, также известны как производные маски. Потому что, как мы уже неоднократно заявляли в этой серии уроков, изображение также является сигналом, поэтому изменения в сигнале можно рассчитать только с использованием дифференцирования. Вот почему эти операторы также называются производными операторами или производными масками.

Все производные маски должны иметь следующие свойства:

• Противоположный знак должен присутствовать в маске.

• Сумма маски должна быть равна нулю.

• Больший вес означает большее обнаружение края.

Противоположный знак должен присутствовать в маске.

Сумма маски должна быть равна нулю.

Больший вес означает большее обнаружение края.

Оператор Prewitt предоставляет нам две маски: одну для обнаружения краев в горизонтальном направлении, а другую для обнаружения краев в вертикальном направлении.

Вертикальное направление:

-1	0	1
-1	0	1
-1	0	1

Над маской найдут ребра в вертикальном направлении, и это потому, что столбцы нулей в вертикальном направлении. Когда вы свернете эту маску на изображении, она даст вам вертикальные края на изображении.

Как это устроено:

Когда мы применяем эту маску к изображению, на ней выступают вертикальные края. Он просто работает как производный первого порядка и рассчитывает разницу интенсивностей пикселей в краевой области. Поскольку центральный столбец имеет нулевое значение, он не включает исходные значения изображения, а скорее вычисляет разницу значений правого и левого пикселей вокруг этого края. Это увеличивает интенсивность края, и это становится лучше по сравнению с исходным изображением.

Горизонтальное направление:

-1	-1	-1
0	0	0
1	1	1

Над маской найдутся ребра в горизонтальном направлении, и это потому, что столбец нулей в горизонтальном направлении. Когда вы свернете эту маску на изображение, на ней будут видны горизонтальные края.

Как это устроено:

Эта маска выделяет горизонтальные края изображения. Он также работает по принципу вышеуказанной маски и рассчитывает разницу между интенсивностями пикселей конкретного края. Поскольку центральный ряд маски состоит из нулей, он не включает в себя исходные значения края в изображении, а скорее рассчитывает разницу между интенсивностями пикселей выше и ниже определенного края. Таким образом увеличивая внезапное изменение интенсивности и делая край более видимым. Обе вышеуказанные маски следуют принципу производной маски. Обе маски имеют противоположный знак, а сумма обеих масок равна нулю. Третье условие не будет применимо в этом операторе, так как обе вышеуказанные маски стандартизированы, и мы не можем изменить значение в них.

Теперь пришло время увидеть эти маски в действии:

Образец изображения:

Ниже приведен пример изображения, на котором мы будем применять две маски по одной за раз.

После нанесения вертикальной маски:

После применения вертикальной маски к приведенному выше образцу изображения будет получено следующее изображение. Это изображение содержит вертикальные края. Вы можете судить об этом более правильно, сравнивая горизонтальные края изображения.

После применения горизонтальной маски:

После применения горизонтальной маски к приведенному выше образцу изображения будет получено следующее изображение.

Сравнение:

Как вы можете видеть, что на первом изображении, к которому мы применяем вертикальную маску, все вертикальные края более заметны, чем исходное изображение. Аналогично на втором рисунке мы применили горизонтальную маску, и в результате все горизонтальные края видны. Таким образом, вы можете видеть, что мы можем обнаружить как горизонтальные, так и вертикальные края изображения.

Собел Оператор

Оператор sobel очень похож на оператор Prewitt. Это также производная маска, которая используется для обнаружения краев. Как и оператор Prewitt, оператор sobel также используется для обнаружения двух видов ребер в изображении:

• Вертикальное направление

• Горизонтальное направление

Вертикальное направление

Горизонтальное направление

Разница с Prewitt оператором:

Основное различие заключается в том, что у оператора sobel коэффициенты масок не являются фиксированными и могут быть скорректированы в соответствии с нашими требованиями, если только они не нарушают какое-либо свойство производных масок.

Ниже приводится вертикальная маска оператора Собеля:

-1	0	1
-2	0	2
-1	0	1

Эта маска работает точно так же, как вертикальная маска оператора Prewitt. Единственное отличие состоит в том, что в центре первого и третьего столбца указаны значения «2» и «-2». При нанесении на изображение эта маска будет подсвечивать вертикальные края.

Как это устроено:

Когда мы применяем эту маску к изображению, на ней выступают вертикальные края. Он просто работает как производный первого порядка и рассчитывает разницу интенсивностей пикселей в краевой области.

Поскольку центральный столбец имеет нулевое значение, он не включает исходные значения изображения, а скорее вычисляет разницу значений правого и левого пикселей вокруг этого края. Также центральные значения как первого, так и третьего столбца составляют 2 и -2 соответственно.

Это дает больший возраст значения пикселов вокруг краевой области. Это увеличивает интенсивность края, и это становится лучше по сравнению с исходным изображением.

Ниже приводится горизонтальная маска оператора Собеля:

-1	-2	-1
0	0	0
1	2	1

Над маской найдутся ребра в горизонтальном направлении, и это потому, что столбец нулей в горизонтальном направлении. Когда вы свернете эту маску на изображение, на ней будут видны горизонтальные края. Единственная разница между ним состоит в том, что он имеет 2 и -2 в качестве центрального элемента первого и третьего ряда.

Как это устроено:

Эта маска выделяет горизонтальные края изображения. Он также работает по принципу вышеуказанной маски и рассчитывает разницу между интенсивностями пикселей конкретного края. Поскольку центральный ряд маски состоит из нулей, он не включает в себя исходные значения края в изображении, а скорее рассчитывает разницу между интенсивностями пикселей выше и ниже определенного края. Таким образом увеличивая внезапное изменение интенсивности и делая край более видимым.

Теперь пришло время увидеть эти маски в действии:

Образец изображения:

Ниже приведен пример изображения, на котором мы будем применять две маски по одной за раз.

После нанесения вертикальной маски:

После применения вертикальной маски к приведенному выше образцу изображения будет получено следующее изображение.

После применения горизонтальной маски:

После применения горизонтальной маски к приведенному выше образцу изображения будет получено следующее изображение.

Сравнение:

Как вы можете видеть, что на первом изображении, к которому мы применяем вертикальную маску, все вертикальные края более заметны, чем исходное изображение. Аналогично на втором рисунке мы применили горизонтальную маску, и в результате все горизонтальные края видны.

Таким образом, вы можете видеть, что мы можем обнаружить как горизонтальные, так и вертикальные края изображения. Также, если вы сравните результат оператора sobel с оператором Prewitt, вы обнаружите, что оператор sobel находит больше ребер или делает ребра более видимыми по сравнению с оператором Prewitt.

Это связано с тем, что в операторе sobel мы уделили больше внимания интенсивности пикселей по краям.

Применяя больший вес для маскировки

Теперь мы также можем видеть, что, если мы применим больший вес к маске, тем больше ребер она получит для нас. Также, как упоминалось в начале урока, что в операторе sobel нет фиксированных коэффициентов, так что вот еще один взвешенный оператор

-1	0	1
-5	0	5
-1	0	1

Если вы можете сравнить результат этой маски с вертикальной маской Prewitt, то ясно, что эта маска даст больше ребер по сравнению с Prewitt только потому, что мы выделили больший вес в маске.

Робинсон Компас Маска

Компасные маски Robinson — это еще один тип дерривата, который используется для обнаружения краев. Этот оператор также известен как маска направления. В этом операторе мы берем одну маску и поворачиваем ее во всех 8 основных направлениях компаса, которые следующие:

• к северу

• северо-Запад

• запад

• Юго-запад

• юг

• Юго Восток

• восток

• к северо-востоку

к северу

северо-Запад

запад

Юго-запад

юг

Юго Восток

восток

к северо-востоку

Там нет фиксированной маски. Вы можете взять любую маску, и вы должны повернуть ее, чтобы найти края во всех вышеупомянутых направлениях. Все маски вращаются по основаниям направления нулевых столбцов.

Например, давайте посмотрим на следующую маску, которая находится в северном направлении, а затем повернем ее, чтобы сделать все маски направления.

Маска северного направления

-1	0	1
-2	0	2
-1	0	1

Северо-западная маска направления

0	1	2
-1	0	1
-2	-1	0

Западная маска направления

1	2	1
0	0	0
-1	-2	-1

Юго-западная маска направления

2	1	0
1	0	-1
0	-1	-2

Маска южного направления

1	0	-1
2	0	-2
1	0	-1

Юго-восточная маска направления

0	-1	-2
1	0	-1
2	1	0

Восточная маска направления

-1	-2	-1
0	0	0
1	2	1

Северо-восточная маска направления

-2	-1	0
-1	0	1
0	1	2

Как вы можете видеть, что все направления покрыты на основе направления нулей. Каждая маска даст вам края по своему направлению. Теперь давайте посмотрим на результат всей вышеупомянутой маски. Предположим, у нас есть образец изображения, из которого мы должны найти все ребра. Вот наш образец изображения:

Образец изображения:

Теперь мы применим все вышеупомянутые фильтры к этому изображению и получим следующий результат.

Северное направление края

Северо-западное направление

Западное направление края

Край юго-западного направления

Южное направление края

Край юго-восточного направления

Край восточного направления

Край северо-восточного направления

Как вы можете видеть, применяя все вышеупомянутые маски, вы получите края во всех направлениях. Результат также зависит от изображения. Предположим, что есть изображение, у которого нет краев в северо-восточном направлении, поэтому эта маска будет неэффективна.

Криш Компас Маска

Kirsch Compass Mask также является производной маской, которая используется для нахождения ребер. Это также похоже на то, как компас Робинсона находит ребра во всех восьми направлениях компаса. Единственное различие между масками Робинсона и компаса Кирша состоит в том, что в Кирше у нас есть стандартная маска, но в Кирше мы меняем маску в соответствии с нашими собственными требованиями.

С помощью масок компаса Кирша мы можем найти ребра в следующих восьми направлениях.

• к северу

• северо-Запад

• запад

• Юго-запад

• юг

• Юго Восток

• восток

• к северо-востоку

к северу

северо-Запад

запад

Юго-запад

юг

Юго Восток

восток

к северо-востоку

Мы берем стандартную маску, которая следует всем свойствам производной маски, а затем поворачиваем ее, чтобы найти ребра.

Например, давайте посмотрим на следующую маску, которая находится в северном направлении, а затем повернем ее, чтобы сделать все маски направления.

Маска северного направления

-3	-3	5
-3	0	5
-3	-3	5

Северо-западная маска направления

-3	5	5
-3	0	5
-3	-3	-3

Западная маска направления

5	5	5
-3	0	-3
-3	-3	-3

Юго-западная маска направления

5	5	-3
5	0	-3
-3	-3	-3

Маска южного направления

5	-3	-3
5	0	-3
5	-3	-3

Юго-восточная маска направления

-3	-3	-3
5	0	-3
5	5	-3

Восточная маска направления

-3	-3	-3
-3	0	-3
5	5	5

Северо-восточная маска направления

-3	-3	-3
-3	0	5
-3	5	5

Как вы можете видеть, что все направления покрыты, и каждая маска даст вам края своего собственного направления. Теперь, чтобы помочь вам лучше понять концепцию этих масок, мы применим их к реальному изображению. Предположим, у нас есть образец изображения, из которого мы должны найти все ребра. Вот наш образец изображения:

Образец изображения

Теперь мы применим все вышеупомянутые фильтры к этому изображению и получим следующий результат.

Северное направление края

Северо-западное направление

Западное направление края

Край юго-западного направления

Южное направление края

Край юго-восточного направления

Край восточного направления

Край северо-восточного направления

Как вы можете видеть, применяя все вышеупомянутые маски, вы получите края во всех направлениях. Результат также зависит от изображения. Предположим, что есть изображение, у которого нет краев в северо-восточном направлении, поэтому эта маска будет неэффективна.

Лапласианский оператор

Оператор Лапласа также является производным оператором, который используется для поиска ребер в изображении. Основное различие между лапласианом и другими операторами, такими как Prewitt, Sobel, Robinson и Kirsch, заключается в том, что все они являются производными масками первого порядка, а Laplacian — производными масками второго порядка. В этой маске у нас есть еще две классификации: одна — положительный оператор Лапласа, а другая — отрицательный оператор Лапласа.

Другое различие между лапласианом и другими операторами состоит в том, что в отличие от других операторов лапласиан не вынимает ребра в каком-либо конкретном направлении, но вынимает ребра в следующей классификации.

• Внутренние края

• Внешние края

Внутренние края

Внешние края

Давайте посмотрим, как работает оператор Лапласа.

Положительный оператор Лапласа:

В положительном лапласиане у нас есть стандартная маска, в которой центральный элемент маски должен быть отрицательным, а угловые элементы маски должны быть равны нулю.

0	1	0
1	-4	1
0	1	0

Положительный оператор Лапласа используется для удаления внешних краев на изображении.

Отрицательный оператор Лапласа:

В отрицательном операторе Лапласа у нас также есть стандартная маска, в которой центральный элемент должен быть положительным. Все элементы в углу должны быть равны нулю, а остальные элементы в маске должны быть равны -1.

0	-1	0
-1	4	-1
0	-1	0

Отрицательный оператор Лапласа используется для удаления внутренних краев в изображении

Как это устроено:

Лапласиан является производным оператором; он использует выделение неоднородностей уровня серого в изображении и пытается выделить области с медленно меняющимися уровнями серого. В результате этой операции создаются такие изображения, которые имеют сероватые края и другие неоднородности на темном фоне. Это создает внутренние и внешние края изображения

Важно то, как применить эти фильтры к изображению. Помните, что мы не можем применять как положительный, так и отрицательный оператор Лапласа к одному и тому же изображению. мы должны применить только одно, но следует помнить, что если мы применим положительный оператор Лапласа к изображению, то мы вычтем результирующее изображение из исходного изображения, чтобы получить заостренное изображение. Аналогично, если мы применяем отрицательный оператор Лапласа, то мы должны добавить результирующее изображение к исходному изображению, чтобы получить заостренное изображение.

Давайте применим эти фильтры к изображению и посмотрим, как он получит нас от внутренних и внешних краев изображения. Предположим, у нас есть следующий пример изображения.

Образец изображения

После применения положительного оператора Лапласа:

После применения положительного оператора Лапласа мы получим следующее изображение.

После применения отрицательного оператора Лапласа:

После применения отрицательного оператора Лапласа мы получим следующее изображение.

Введение в частотную область

Мы имеем дело с изображениями во многих областях. Сейчас мы обрабатываем сигналы (изображения) в частотной области. Поскольку этот ряд Фурье и частотная область являются чисто математическими, поэтому мы постараемся свести к минимуму эту математическую часть и уделить больше внимания ее использованию в DIP.

Анализ частотной области

До сих пор все домены, в которых мы анализировали сигнал, анализируем его по времени. Но в частотной области мы анализируем сигнал не по времени, а по частоте.

Разница между пространственной и частотной областями.

В пространственной области мы имеем дело с изображениями как есть. Значение пикселей изображения изменяется относительно сцены. В то время как в частотной области мы имеем дело со скоростью, с которой значения пикселей изменяются в пространственной области.

Давайте для простоты скажем так.

Пространственный домен

В простой пространственной области мы имеем дело непосредственно с матрицей изображения. Тогда как в частотной области мы имеем дело с изображением, подобным этому.

Частотная область

Сначала мы преобразуем изображение в его частотное распределение. Затем наша система «черного ящика» выполняет все необходимые операции, и в этом случае вывод черного ящика — это не изображение, а преобразование. После выполнения обратного преобразования оно преобразуется в изображение, которое затем просматривается в пространственной области.

Это можно наглядно рассматривать как

Здесь мы использовали слово трансформация. Что это на самом деле означает?

Трансформации.

Сигнал может быть преобразован из временной области в частотную область с использованием математических операторов, называемых преобразованиями. Есть много видов трансформации, которые делают это. Некоторые из них приведены ниже.

• Серия Фурье

• Преобразование Фурье

• Преобразование Лапласа

• Z преобразование

Серия Фурье

Преобразование Фурье

Преобразование Лапласа

Z преобразование

Из всего этого мы подробно обсудим ряды Фурье и преобразование Фурье в нашем следующем уроке.

Частотные составляющие

Любое изображение в пространственной области может быть представлено в частотной области. Но что на самом деле означают эти частоты?

Мы разделим частотные составляющие на два основных компонента.

Высокочастотные компоненты

Высокочастотные компоненты соответствуют краям изображения.

Низкочастотные компоненты

Низкочастотные составляющие в изображении соответствуют гладким областям.

Ряд Фурье и преобразование

В последнем уроке анализа частотной области мы обсуждали, что ряд Фурье и преобразование Фурье используются для преобразования сигнала в частотную область.

Фурье

Фурье был математиком в 1822 году. Он дал ряд Фурье и преобразование Фурье для преобразования сигнала в частотную область.

Серия Фурье

Ряд Фурье просто утверждает, что периодические сигналы могут быть представлены в виде суммы синусов и косинусов при умножении на определенный вес. Далее утверждается, что периодические сигналы могут быть разбиты на дополнительные сигналы со следующими свойствами.

• Сигналы синусы и косинусы

• Сигналы являются гармониками друг друга

Сигналы синусы и косинусы

Сигналы являются гармониками друг друга

Это можно наглядно рассматривать как

В приведенном выше сигнале последний сигнал фактически является суммой всех вышеуказанных сигналов. Это была идея Фурье.

Как это рассчитывается.

Поскольку, как мы видели в частотной области, чтобы обработать изображение в частотной области, нам нужно сначала преобразовать его, используя в частотную область, и мы должны взять обратный выходной сигнал, чтобы преобразовать его обратно в пространственную область. Поэтому и ряд Фурье, и преобразование Фурье имеют две формулы. Один для преобразования и один преобразование обратно в пространственную область.

Ряд Фурье

Ряд Фурье можно обозначить этой формулой.

Обратное можно рассчитать по этой формуле.

преобразование Фурье

Преобразование Фурье просто утверждает, что непериодические сигналы, площадь которых под кривой конечна, также могут быть представлены в интегралах от синусов и косинусов после умножения на определенный вес.

Преобразование Фурье имеет много широких применений, включая сжатие изображений (например, JPEG-сжатие), фильтрацию и анализ изображений.

Разница между рядами Фурье и преобразованием

Хотя и ряд Фурье, и преобразование Фурье задаются Фурье, но разница между ними заключается в том, что ряд Фурье применяется к периодическим сигналам, а преобразование Фурье применяется к непериодическим сигналам.

Какой из них применяется к изображениям.

Теперь вопрос заключается в том, какой из них применяется к изображениям: ряд Фурье или преобразование Фурье. Ну, ответ на этот вопрос заключается в том, что изображения. Изображения непериодические. А поскольку изображения непериодические, поэтому преобразование Фурье используется для их преобразования в частотную область.

Дискретное преобразование Фурье.

Поскольку мы имеем дело с изображениями и воздействуем на цифровые изображения, поэтому для цифровых изображений мы будем работать над дискретным преобразованием Фурье

Рассмотрим вышеупомянутый член Фурье синусоиды. Это включает в себя три вещи.

• Пространственная частота

• величина

• фаза

Пространственная частота

величина

фаза

Пространственная частота напрямую связана с яркостью изображения. Величина синусоиды напрямую связана с контрастом. Контрастность — это разница между максимальной и минимальной интенсивностью пикселей. Фаза содержит информацию о цвете.

Формула для двумерного дискретного преобразования Фурье приведена ниже.

Дискретное преобразование Фурье на самом деле является дискретизированным преобразованием Фурье, поэтому оно содержит несколько выборок, обозначающих изображение. В приведенной выше формуле f (x, y) обозначает изображение, а F (u, v) обозначает дискретное преобразование Фурье. Формула для двумерного обратного дискретного преобразования Фурье приведена ниже.

Обратное дискретное преобразование Фурье преобразует преобразование Фурье обратно в изображение

Рассмотрим этот сигнал.

Теперь мы увидим изображение, для которого мы рассчитаем спектр величин БПФ, а затем смещенный спектр величин БПФ, а затем возьмем Log этого смещенного спектра.

Исходное изображение

Спектр величин преобразования Фурье

Сдвинутое преобразование Фурье

Сдвинутый Спектр Величины

Теорема свертки

В последнем уроке мы обсуждали изображения в частотной области. В этом уроке мы собираемся определить связь между частотной областью и изображениями (пространственная область).

Например:

Рассмотрим этот пример.

То же изображение в частотной области может быть представлено как.

Теперь, какова связь между изображением или пространственной областью и частотной областью. Это соотношение может быть объяснено теоремой, которая называется теоремой свертки.

Теорема свертки

Связь между пространственной областью и частотной областью может быть установлена ​​с помощью теоремы свертки.

Теорема свертки может быть представлена ​​как.

Можно констатировать, что свертка в пространственной области равна фильтрации в частотной области и наоборот.

Фильтрация в частотной области может быть представлена ​​следующим образом:

Шаги в фильтрации приведены ниже.

• На первом этапе мы должны сделать некоторую предварительную обработку изображения в пространственной области, что означает увеличение его контрастности или яркости.

• Тогда мы возьмем дискретное преобразование Фурье изображения

• Затем мы будем центрировать дискретное преобразование Фурье, так как мы приведем дискретное преобразование Фурье в центр от углов

• Затем мы применим фильтрацию, то есть умножим преобразование Фурье на функцию фильтра.

• Тогда мы снова сместим ДПФ от центра к углам

• Последний шаг — обратное дискретное преобразование Фурье, чтобы вернуть результат из частотной области в пространственную.

• И этот шаг постобработки является необязательным, как и предварительная обработка, в которой мы просто увеличиваем внешний вид изображения.

На первом этапе мы должны сделать некоторую предварительную обработку изображения в пространственной области, что означает увеличение его контрастности или яркости.

Тогда мы возьмем дискретное преобразование Фурье изображения

Затем мы будем центрировать дискретное преобразование Фурье, так как мы приведем дискретное преобразование Фурье в центр от углов

Затем мы применим фильтрацию, то есть умножим преобразование Фурье на функцию фильтра.

Тогда мы снова сместим ДПФ от центра к углам

Последний шаг — обратное дискретное преобразование Фурье, чтобы вернуть результат из частотной области в пространственную.

И этот шаг постобработки является необязательным, как и предварительная обработка, в которой мы просто увеличиваем внешний вид изображения.

фильтры

Концепция фильтра в частотной области аналогична концепции маски в свертке.

После преобразования изображения в частотную область некоторые фильтры применяются в процессе фильтрации для выполнения различного рода обработки изображения. Обработка включает в себя размытие изображения, резкость изображения и т. Д.

Общий тип фильтров для этих целей:

• Идеальный фильтр верхних частот

• Идеальный фильтр низких частот

• Гауссовский фильтр верхних частот

• Гауссовский фильтр нижних частот

Идеальный фильтр верхних частот

Идеальный фильтр низких частот

Гауссовский фильтр верхних частот

Гауссовский фильтр нижних частот

В следующем уроке мы подробно обсудим фильтр.

Фильтры высоких частот против фильтров низких частот

В последнем уроке мы кратко обсудим фильтры. В этом уроке мы подробно обсудим их. Прежде чем обсуждать, давайте сначала поговорим о масках. Концепция маски была обсуждена в нашем уроке свертки и масок.

Размытые маски против производных масок.

Мы собираемся выполнить сравнение между размывающими масками и производными масками.

Размытые маски:

Размытая маска обладает следующими свойствами.

• Все значения в размывающих масках положительны

• Сумма всех значений равна 1

• Содержание края уменьшается с помощью маски размытия

• По мере роста размера маски будет происходить более сглаживающий эффект

Все значения в размывающих масках положительны

Сумма всех значений равна 1

Содержание края уменьшается с помощью маски размытия

По мере роста размера маски будет происходить более сглаживающий эффект

Производные маски:

Производная маска обладает следующими свойствами.

• Производная маска имеет как положительные, так и отрицательные значения

• Сумма всех значений в производной маске равна нулю

• Содержимое края увеличивается производной маской

• По мере увеличения размера маски увеличивается количество краев

Производная маска имеет как положительные, так и отрицательные значения

Сумма всех значений в производной маске равна нулю

Содержимое края увеличивается производной маской

По мере увеличения размера маски увеличивается количество краев

Связь между маской размытия и производной маской с фильтрами верхних частот и фильтрами нижних частот.

Соотношение между маской размытия и производной маской с фильтром верхних частот и фильтром нижних частот можно определить просто как.

• Размытые маски также называются фильтром нижних частот

• Производные маски также называются фильтром верхних частот

Размытые маски также называются фильтром нижних частот

Производные маски также называются фильтром верхних частот

Высокочастотные частотные компоненты и Низкочастотные частотные компоненты

Компоненты частоты верхних частот обозначают ребра, тогда как компоненты частоты нижних частот обозначают гладкие области.

Идеальные фильтры низких частот и Идеальные фильтры высоких частот

Это общий пример фильтра нижних частот.

Когда один помещен внутрь, а ноль размещен снаружи, мы получили размытое изображение. Теперь, когда мы увеличиваем размер 1, размытие будет увеличено, а содержимое края будет уменьшено.

Это общий пример фильтра верхних частот.

Когда 0 помещается внутрь, мы получаем ребра, что дает нам эскизное изображение. Идеальный фильтр нижних частот в частотной области приведен ниже

Идеальный фильтр нижних частот может быть графически представлен как

Теперь давайте применим этот фильтр к реальному изображению и посмотрим, что мы получили.

Образец изображения.

Изображение в частотной области

Применение фильтра к этому изображению

Результирующее изображение

Таким же образом идеальный фильтр верхних частот может быть применен к изображению. Но очевидно, что результаты будут другими, поскольку нижний проход уменьшает острое содержимое, а верхний — увеличивает его.

Гауссовский фильтр низких частот и гауссовский фильтр высоких частот

Гауссовский фильтр нижних частот и гауссовский фильтр верхних частот минимизируют проблему, возникающую в идеальном фильтре нижних частот и верхних частот.

Эта проблема известна как эффект звонка. Это связано с причиной, потому что в некоторых точках переход от одного цвета к другому не может быть точно определен, из-за чего в этой точке возникает эффект звонка.

Посмотрите на этот график.

Это представление идеального фильтра нижних частот. Теперь, в точной точке Do, вы не можете сказать, что значение будет 0 или 1. Из-за этого в этой точке появляется эффект вызова.

Таким образом, чтобы уменьшить эффект, который проявляется в идеальном низкочастотном и идеальном высокочастотном фильтрах, введены следующий гауссовский фильтр нижних частот и гауссовский фильтр верхних частот.

Гауссовский фильтр нижних частот

Концепция фильтрации и низких частот остается прежней, но только переход становится другим и становится более плавным.

Фильтр нижних частот Гаусса может быть представлен как

Обратите внимание на плавный переход кривой, благодаря которому в каждой точке значение Do может быть точно определено.

Гауссовский фильтр верхних частот

Фильтр верхних частот Гаусса имеет ту же концепцию, что и идеальный фильтр верхних частот, но опять-таки переход более плавный по сравнению с идеальным.

Введение в цветовые пространства

В этом уроке мы поговорим о цветовых пространствах.

Что такое цветовые пространства?

Цветовые пространства — это различные типы цветовых режимов, используемые при обработке изображений и сигналов и системы для различных целей. Некоторые из распространенных цветовых пространств:

• RGB

• CMY’K

• Y’UV

• YIQ

• Y’CbCr

• HSV

RGB

CMY’K

Y’UV

YIQ

Y’CbCr

HSV

RGB

RGB является наиболее широко используемым цветовым пространством, и мы уже обсуждали его в предыдущих уроках. RGB означает красный, зеленый и синий.

Что говорит модель RGB, что каждое цветное изображение фактически состоит из трех разных изображений. Красное изображение, синее изображение и черное изображение. Нормальное изображение в градациях серого может быть определено только одной матрицей, но цветное изображение фактически состоит из трех разных матриц.

Одноцветная матрица изображения = красная матрица + синяя матрица + зеленая матрица

Это лучше всего видно в этом примере ниже.

Приложения RGB

Общие применения модели RGB:

• Катодно-лучевая трубка (ЭЛТ)

• Жидкокристаллический дисплей (LCD)

• Плазменный дисплей или светодиодный дисплей, такой как телевизор

• Вычислительный монитор или большой экран

Катодно-лучевая трубка (ЭЛТ)

Жидкокристаллический дисплей (LCD)

Плазменный дисплей или светодиодный дисплей, такой как телевизор

Вычислительный монитор или большой экран

CMYK

Преобразование RGB в CMY

Преобразование из RGB в CMY выполняется с помощью этого метода.

Предположим, у вас есть цветное изображение, это означает, что у вас есть три разных массива RED, GREEN и BLUE. Теперь, если вы хотите конвертировать его в CMY, вот что вам нужно сделать. Вы должны вычесть это из максимального количества уровней — 1. Каждая матрица вычитается, и ее соответствующая матрица CMY заполняется результатом.

Y’UV

Y’UV определяет цветовое пространство в единицах яркости (Y ‘) и двух компонентах цветности (УФ). Цветовая модель Y’UV используется в следующих стандартах композитного цветного видео.

• NTSC (Национальный комитет по телевизионным системам)

• PAL (фазово-чередующаяся линия)

• SECAM («Последовательный фильм», по-французски «последовательный цвет с памятью»)

NTSC (Национальный комитет по телевизионным системам)

PAL (фазово-чередующаяся линия)

SECAM («Последовательный фильм», по-французски «последовательный цвет с памятью»)

Y’CbCr

Цветовая модель Y’CbCr содержит Y ‘, компонент яркости, а cb и cr — компоненты синего и красного цветов.

Это не абсолютное цветовое пространство. В основном используется для цифровых систем

Его общие приложения включают сжатие JPEG и MPEG.

Y’UV часто используется как термин для Y’CbCr, однако это совершенно разные форматы. Основное различие между ними состоит в том, что первый является аналоговым, а второй — цифровым.

Введение в сжатие JPEG

В нашем последнем уроке сжатия изображений мы обсудим некоторые методы, используемые для сжатия

Мы собираемся обсудить сжатие JPEG, которое представляет собой сжатие с потерями, поскольку некоторые данные в конечном итоге теряются.

Давайте сначала обсудим, что такое сжатие изображений.

Сжатие изображения

Сжатие изображений — это метод сжатия данных на цифровых изображениях.

Основной целью сжатия изображений является:

• Храните данные в эффективной форме

• Передача данных в эффективной форме

Храните данные в эффективной форме

Передача данных в эффективной форме

Сжатие изображения может быть с потерями или без потерь.

Сжатие JPEG

JPEG обозначает Объединенную группу экспертов по фотографии. Это первый международный стандарт сжатия изображений. Это широко используется сегодня. Это может быть как с потерями, так и без потерь. Но техника, которую мы собираемся обсудить здесь сегодня, это техника сжатия с потерями.

Как работает сжатие JPEG:

Первый шаг — разделить изображение на блоки, каждый из которых имеет размеры 8х8.

Допустим, скажем, что это изображение 8×8 содержит следующие значения.

Диапазон интенсивностей пикселей теперь составляет от 0 до 255. Мы изменим диапазон с -128 до 127.

Вычитание 128 из каждого значения пикселя дает значение пикселя от -128 до 127. После вычитания 128 из каждого значения пикселя мы получили следующие результаты.

Теперь мы будем вычислять, используя эту формулу.

Полученный результат сохраняется в, скажем, матрице A (j, k).

Существует стандартная матрица, которая используется для вычисления сжатия JPEG, которая задается матрицей, называемой матрицей яркости.

Эта матрица приведена ниже

Применяя следующую формулу

Мы получили этот результат после подачи заявки.

Теперь мы выполним настоящий трюк, который делается в сжатии JPEG, который представляет собой движение ZIG-ZAG. Последовательность зигзага для вышеуказанной матрицы показана ниже. Вы должны выполнять зигзаг, пока не найдете все нули впереди. Следовательно, наше изображение теперь сжато.

Подводя итоги сжатия JPEG

Первый шаг — преобразовать изображение в Y’CbCr и просто выбрать канал Y ‘и разбить его на 8 × 8 блоков. Затем, начиная с первого блока, отобразите диапазон от -128 до 127. После этого вам нужно найти дискретное преобразование Фурье матрицы. Результат этого должен быть квантован. Последний шаг — применить кодирование зигзагообразно и делать это, пока вы не найдете все ноль.

Сохраните этот одномерный массив, и все готово.

Заметка. Вы должны повторить эту процедуру для всего блока 8 х 8.

Оптическое распознавание символов

Оптическое распознавание символов обычно сокращается как OCR. Он включает механическое и электрическое преобразование отсканированных изображений рукописного, машинописного текста в машинный текст. Это распространенный метод оцифровки печатных текстов, чтобы их можно было искать в электронном виде, хранить более компактно, отображать в режиме онлайн и использовать в машинных процессах, таких как машинный перевод, преобразование текста в речь и интеллектуальный анализ текста.

В последние годы технология оптического распознавания символов (OCR) применяется во всем спектре отраслей, что революционизирует процесс управления документами. OCR позволил отсканированным документам превратиться в нечто большее, чем просто файлы изображений, превратившись в полностью доступные для поиска документы с текстовым содержимым, распознаваемым компьютерами. С помощью OCR людям больше не нужно вручную перепечатывать важные документы при вводе их в электронные базы данных. Вместо этого OCR извлекает соответствующую информацию и вводит ее автоматически. Результат — точная и эффективная обработка информации за меньшее время.

Оптическое распознавание символов имеет несколько областей исследования, но наиболее распространенными являются следующие:

Банковское дело:

Он использует OCR в разных областях. Одним из широко известных приложений является банковское дело, где OCR используется для обработки чеков без участия человека. Чек может быть вставлен в машину, надпись на нем сканируется мгновенно, и переводится правильная сумма. Эта технология почти усовершенствована для печатных чеков, и она достаточно точна и для рукописных чеков, хотя иногда требует ручного подтверждения. В целом, это сокращает время ожидания во многих банках.

Слепые и слабовидящие люди:

Одним из основных факторов в начале исследования OCR является то, что ученые хотят создать компьютер или устройство, которое могло бы вслух читать книги слепым людям. Для этого исследования ученый сделал планшетный сканер, который чаще всего известен нам как сканер документов.

Юридический отдел:

В юридической отрасли также произошло значительное движение по оцифровке бумажных документов. В целях экономии места и устранения необходимости просеивать через коробки бумажных файлов документы сканируются и заносятся в компьютерные базы данных. OCR дополнительно упрощает процесс, делая документы доступными для поиска по тексту, чтобы их было легче найти и работать с ними один раз в базе данных. Теперь юристы имеют быстрый и легкий доступ к огромной библиотеке документов в электронном формате, которую можно найти, просто набрав несколько ключевых слов.

Розничной торговли:

Технология распознавания штрих-кода также связана с OCR. Мы видим использование этой технологии в нашем обычном повседневном использовании.

Другое использование:

OCR широко используется во многих других областях, включая образование, финансы и государственные учреждения. OCR сделал бесчисленные тексты доступными в Интернете, что экономит деньги для студентов и позволяет делиться знаниями. Приложения для обработки счетов используются во многих компаниях для отслеживания финансовых отчетов и предотвращения накопления накопившихся платежей. В государственных учреждениях и независимых организациях OCR упрощает сбор и анализ данных, в том числе. Поскольку технология продолжает развиваться, все больше и больше приложений используются для технологии OCR, включая более широкое использование распознавания рукописного ввода.

Компьютерное зрение и компьютерная графика

Компьютерное зрение

Компьютерное зрение связано с моделированием и копированием человеческого зрения с использованием компьютерного программного и аппаратного обеспечения. Формально, если мы определим компьютерное зрение, то его определение будет таким, что компьютерное зрение — это дисциплина, которая изучает, как реконструировать, прерывать и понимать трехмерную сцену из ее 2-мерных изображений с точки зрения свойств структуры, присутствующей в сцене.

Для понимания и стимулирования работы системы человеческого зрения необходимы знания из следующих областей.

• Информатика

• Электротехника

• Математика

• физиология

• Биология

• Когнитивная наука

Информатика

Электротехника

Математика

физиология

Биология

Когнитивная наука

Иерархия компьютерного зрения:

Компьютерное зрение делится на три основные категории:

Низкоуровневое зрение: включает изображение процесса для извлечения объектов.

Видение среднего уровня: включает в себя распознавание объектов и интерпретацию 3D-сцены

Видение высокого уровня: включает концептуальное описание сцены, такой как деятельность, намерение и поведение.

Связанные поля:

Computer Vision значительно перекрывает следующие поля:

Обработка изображений: фокусируется на манипулировании изображениями.

Распознавание паттернов: изучает различные методы классификации паттернов.

Фотограмметрия: это связано с получением точных измерений из изображений.

Computer Vision Vs Обработка изображений:

Обработка изображений изучает преобразование изображения в изображение. Вход и выход обработки изображения оба изображения.

Компьютерное зрение — это построение явных, значимых описаний физических объектов по их изображению. Результатом компьютерного зрения является описание или интерпретация структур в трехмерной сцене.

Примеры приложений:

• робототехника

• Лекарственное средство

• Безопасность

• Транспорт

• Индустриальная автоматизация

робототехника

Лекарственное средство

Безопасность

Транспорт

Индустриальная автоматизация

Применение робототехники:

• Локализация — определить местоположение робота автоматически

• навигация

• Избегание препятствий

• Сборка (колышек, сварка, покраска)

• Манипуляции (например, робот-манипулятор PUMA)

• Human Robot Interaction (HRI): интеллектуальная робототехника для взаимодействия и обслуживания людей

Локализация — определить местоположение робота автоматически

навигация

Избегание препятствий

Сборка (колышек, сварка, покраска)

Манипуляции (например, робот-манипулятор PUMA)

Human Robot Interaction (HRI): интеллектуальная робототехника для взаимодействия и обслуживания людей

Применение в медицине:

• Классификация и обнаружение (например, классификация повреждения или клеток и обнаружение опухоли)

• 2D / 3D сегментация

• 3D реконструкция человеческого органа (МРТ или УЗИ)

• Визуальная робототехника

Классификация и обнаружение (например, классификация повреждения или клеток и обнаружение опухоли)

2D / 3D сегментация

3D реконструкция человеческого органа (МРТ или УЗИ)

Визуальная робототехника

Применение промышленной автоматизации:

• Промышленный контроль (обнаружение дефектов)

• сборочный

• Считывание штрих-кода и этикетки на упаковке

• Сортировка объектов

• Понимание документа (например, OCR)

Промышленный контроль (обнаружение дефектов)

сборочный

Считывание штрих-кода и этикетки на упаковке

Сортировка объектов

Понимание документа (например, OCR)

Приложение безопасности:

• Биометрия (радужная оболочка, отпечаток пальца, распознавание лица)

• Наблюдение — обнаружение определенных подозрительных действий или поведения

Биометрия (радужная оболочка, отпечаток пальца, распознавание лица)

Наблюдение — обнаружение определенных подозрительных действий или поведения

Транспортное приложение:

• Автономное транспортное средство

• Безопасность, например, мониторинг бдительности водителя

Автономное транспортное средство

Безопасность, например, мониторинг бдительности водителя

Компьютерная графика

Компьютерная графика — это графика, созданная с использованием компьютеров, и представление данных изображения компьютером специально с помощью специализированного графического оборудования и программного обеспечения. Формально можно сказать, что компьютерная графика — это создание, манипулирование и хранение геометрических объектов (моделирование) и их изображений (рендеринг).

Область компьютерной графики развивалась с появлением компьютерной графики. Сегодня компьютерная графика используется практически во всех областях. Многие мощные инструменты были разработаны для визуализации данных. Область компьютерной графики стала более популярной, когда компании начали использовать ее в видеоиграх. Сегодня это многомиллиардная индустрия и основная движущая сила развития компьютерной графики. Некоторые общие области применения следующие:

Компьютерный дизайн (САПР)

Графика презентации

3d анимация

Образование и обучение

Графические пользовательские интерфейсы

Используется в дизайне зданий, автомобилей, самолетов и многих других продуктов

Используйте, чтобы сделать систему виртуальной реальности.

Обычно используется для обобщения финансовых, статистических данных

Используйте для создания слайдов

Используется в киноиндустрии такими компаниями, как Pixar, DresmsWorks

Чтобы добавить спецэффекты в играх и фильмах.

Компьютерные модели физических систем

Медицинская визуализация

3D МРТ

Стоматологический и костный сканы

Стимуляторы для обучения пилотов и т. Д.

Он используется для создания объектов графического интерфейса пользователя, таких как кнопки, значки и другие компоненты