Выход большинства датчиков изображения является аналоговым сигналом, и мы не можем применить к нему цифровую обработку, потому что мы не можем его сохранить. Мы не можем сохранить его, потому что он требует бесконечной памяти для хранения сигнала, который может иметь бесконечные значения.
Таким образом, мы должны преобразовать аналоговый сигнал в цифровой сигнал.
Чтобы создать цифровое изображение, нам нужно преобразовать непрерывные данные в цифровую форму. Есть два шага, в которых это делается.
- отбор проб
- квантование
Мы обсудим выборку сейчас, а квантование будет обсуждаться позже, а пока мы немного обсудим разницу между этими двумя и необходимость этих двух шагов.
Основная идея:
Основная идея преобразования аналогового сигнала в цифровой:
преобразовать обе его оси (х, у) в цифровой формат.
Поскольку изображение непрерывно не только по своим координатам (ось x), но и по его амплитуде (ось y), поэтому часть, которая занимается оцифровкой координат, называется выборкой. И часть, которая имеет дело с оцифровкой амплитуды, известна как квантование.
Отбор проб.
Выборка уже была представлена в нашем уроке введения в сигналы и систему. Но мы собираемся обсудить здесь больше.
Вот что мы обсудили из выборки.
Термин «выборка» относится к отбору проб
Оцифровываем ось х в выборке
Это делается на независимой переменной
В случае уравнения y = sin (x) это делается для переменной x
Далее он делится на две части: восходящий и нисходящий
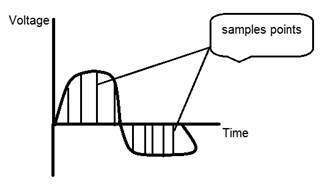
Если вы посмотрите на рисунок выше, вы увидите, что в сигнале есть некоторые случайные изменения. Эти изменения происходят из-за шума. При выборке мы уменьшаем этот шум, отбирая образцы. Очевидно, что чем больше выборок мы берем, тем лучше будет качество изображения, тем больше будет шума, и наоборот.
Однако, если вы берете выборку по оси x, сигнал не преобразуется в цифровой формат, если только вы не берете выборку по оси y, которая известна как квантование. Чем больше выборок в конечном итоге означает, что вы собираете больше данных, а в случае изображения — больше пикселей.
Отношение корабль с пикселями
Поскольку пиксель является наименьшим элементом в изображении. Общее количество пикселей в изображении может быть рассчитано как
Пиксели = общее количество строк * общее количество столбцов.
Допустим, у нас всего 25 пикселей, это означает, что у нас квадратное изображение 5 X 5. Тогда, как мы уже говорили выше при выборке, что больше выборок в конечном итоге приводит к большему количеству пикселей. Таким образом, это означает, что из нашего непрерывного сигнала мы взяли 25 выборок по оси x. Это относится к 25 пикселям этого изображения.
Это приводит к другому выводу, что, поскольку пиксель также является наименьшим делением матрицы ПЗС. Таким образом, это означает, что он также связан с массивом CCD, что можно объяснить следующим образом.
Связь с массивом CCD
Количество датчиков в матрице ПЗС прямо равно количеству пикселей. И поскольку мы пришли к выводу, что количество пикселей прямо равно количеству отсчетов, это означает, что число отсчетов прямо равно количеству датчиков в матрице ПЗС.
Передискретизации.
В начале мы определили, что выборка делится на два типа. Что вверх по выборке и вниз по выборке. Повышенная выборка также называется избыточной выборкой.
Передискретизация имеет очень глубокое применение в обработке изображений, которая называется Zooming.
Масштабирование
Мы официально представим масштабирование в следующем уроке, но сейчас мы кратко объясним масштабирование.
Масштабирование относится к увеличению количества пикселей, поэтому при увеличении изображения вы увидите больше деталей.
Увеличение количества пикселей осуществляется за счет передискретизации. Один из способов увеличения или увеличения выборки заключается в оптическом увеличении с помощью движения объектива и последующем захвате изображения. Но мы должны сделать это, как только изображение будет снято.
Существует разница между масштабированием и выборкой
Концепция та же, то есть увеличение образцов. Но ключевое отличие состоит в том, что, хотя дискретизация выполняется для сигналов, масштабирование выполняется для цифрового изображения.