В последнем уроке мы кратко обсудим фильтры. В этом уроке мы подробно обсудим их. Прежде чем обсуждать, давайте сначала поговорим о масках. Концепция маски была обсуждена в нашем уроке свертки и масок.
Размытые маски против производных масок
Мы собираемся выполнить сравнение между размывающими масками и производными масками.
Размытые маски
Размытая маска обладает следующими свойствами.
- Все значения в размывающих масках положительны
- Сумма всех значений равна 1
- Содержание края уменьшается с помощью маски размытия
- По мере роста размера маски будет происходить более сглаживающий эффект
Производные маски
Производная маска обладает следующими свойствами.
- Производная маска имеет как положительные, так и отрицательные значения
- Сумма всех значений в производной маске равна нулю
- Содержимое края увеличивается производной маской
- По мере увеличения размера маски увеличивается количество краев
Связь между маской размытия и производной маской с фильтрами верхних частот и фильтрами нижних частот.
Соотношение между маской размытия и производной маской с фильтром верхних частот и фильтром нижних частот можно определить просто как.
- Размытые маски также называются фильтром нижних частот
- Производные маски также называются фильтром верхних частот
Высокочастотные частотные компоненты и Низкочастотные частотные компоненты
Компоненты частоты верхних частот обозначают ребра, тогда как компоненты частоты нижних частот обозначают гладкие области.
Идеальные фильтры низких частот и Идеальные фильтры высоких частот
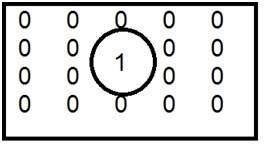
Это общий пример фильтра нижних частот.
Когда один помещен внутрь, а ноль размещен снаружи, мы получили размытое изображение. Теперь, когда мы увеличиваем размер 1, размытие будет увеличено, а содержимое края будет уменьшено.
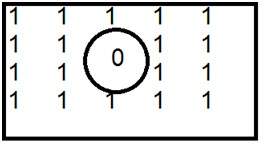
Это общий пример фильтра верхних частот.
Когда 0 помещается внутрь, мы получаем ребра, что дает нам эскизное изображение. Идеальный фильтр нижних частот в частотной области приведен ниже.
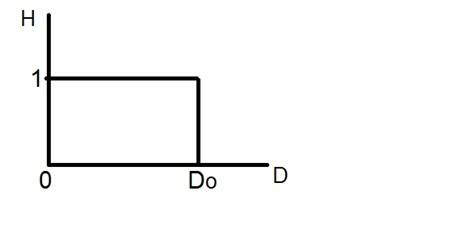
Идеальный фильтр нижних частот может быть графически представлен как
Теперь давайте применим этот фильтр к реальному изображению и посмотрим, что мы получили.
Образец изображения
Изображение в частотной области
Применение фильтра к этому изображению
Результирующее изображение
Таким же образом идеальный фильтр верхних частот может быть применен к изображению. Но очевидно, что результаты будут другими, поскольку нижний проход уменьшает острое содержимое, а верхний — увеличивает его.
Гауссовский фильтр низких частот и гауссовский фильтр высоких частот
Гауссовский фильтр нижних частот и гауссовский фильтр верхних частот минимизируют проблему, возникающую в идеальном фильтре нижних частот и верхних частот.
Эта проблема известна как эффект звонка. Это связано с причиной, потому что в некоторых точках переход от одного цвета к другому не может быть точно определен, из-за чего в этой точке возникает эффект звонка.
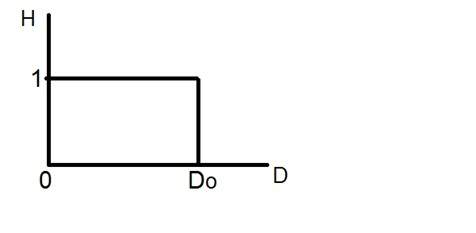
Посмотрите на этот график.
Это представление идеального фильтра нижних частот. Теперь, в точной точке Do, вы не можете сказать, что значение будет 0 или 1. Из-за этого в этой точке появляется эффект вызова.
Таким образом, чтобы уменьшить эффект, который проявляется в идеальном низкочастотном и идеальном высокочастотном фильтрах, введены следующий гауссовский фильтр нижних частот и гауссовский фильтр верхних частот.
Гауссовский фильтр нижних частот
Концепция фильтрации и низких частот остается прежней, но только переход становится другим и становится более плавным.
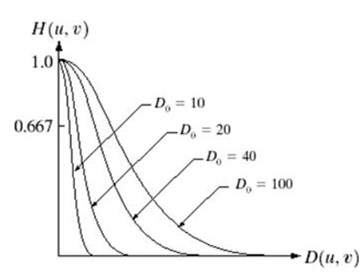
Фильтр нижних частот Гаусса может быть представлен как
Обратите внимание на плавный переход кривой, благодаря которому в каждой точке значение Do может быть точно определено.
Гауссовский фильтр верхних частот
Фильтр верхних частот Гаусса имеет ту же концепцию, что и идеальный фильтр верхних частот, но опять-таки переход более плавный по сравнению с идеальным.