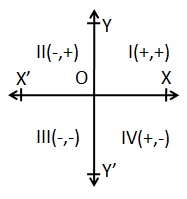
В координатной геометрии точки располагаются на «координатной плоскости», как показано ниже. У него есть две шкалы — одна проходит через плоскость, называемую «осью x», а другая — под прямым углом к оси y. (Они могут рассматриваться как аналогичные столбцу и строке в параграфе выше.) Точка, где оси пересекаются, называется началом координат, и где x и y равны нулю.
На оси абсцисс значения справа положительны, а слева отрицательны. На оси Y значения выше начала координат положительные, а значения ниже отрицательные. Местоположение точки на плоскости задается двумя числами; первый сообщает, где он находится на оси X, а второй — где он находится на оси Y. Вместе они определяют единственную, уникальную позицию на плоскости. Таким образом, на приведенной выше схеме точка A имеет значение x, равное 20, и значение ay, равное 15. Это координаты точки A, иногда называемые ее «прямоугольными координатами».
Обратите внимание, что порядок важен; координата х всегда первая из пары.
Расстояние между двумя точками
Если A (x 1 , y 1 ) и B (x 2 , y 2 ) две точки, то
AB = √ (x 2 -x 1 ) 2 + (y 2 -y 1 ) 2
Расстояние точки от начала координат
Расстояние точки A (x, y) от начала координат O (0, 0) определяется как
ОА = √ (х 2 + у 2 )
Площадь треугольника
Если A (x 1 , y 1 ), B (x 2 , y 2 ) и C = (X 3 , Y 3 ) являются тремя вершинами ∆ABC, то его площадь определяется как:
∆ = 1/2 {x 1 (y 2 - Y 3 ) + x 2 (Y 3 - Y 1 ) + X 3 (y 1 -y 2 )}
Условие коллинеарности трех точек
Три точки A (x 1 , y 1 ), B (x 2 , y 2 ) и C = (X 3 , Y 3 ) коллинеарны тогда и только тогда, когда ar (√ABC) = 0.
∴ A, B, C коллинеарны ⇒ x 1 (y 2 — Y 3 ) + x 2 (Y 3 — Y 1 ) + X 3 (y 1 -y 2 ) = 0
Деление отрезка на точку
Если точка p (x, y) делит объединение A (x 1 , y 1 ) и B (x 2 , y 2 ) в соотношении m: n, то
X = (mx 2 + nx 1 ) / m + n и Y = (my 2 + ny 1 ) / m + n
Если A (x 1 , y 1 ) и B (x 2 , y 2 ) являются конечными точками отрезка AB, то координаты средней точки AB
[(x 1 + x 2 ) / 2, (y 1 + y 2 ) / 2]
Центр тяжести треугольника
Точка пересечения всех медиан треугольника называется его центроидом. Если A (x 1 , y 1 ), B (x 2 , y 2 ) и C = (X 3 , Y 3 ) являются вершинами ABC, то координаты его центроида равны {(1/3 (x 1 + x 2 + x 3 ), 1/3 (y 1 + y 2 + Y 3 )}
Различные типы четырехугольников
Четырехугольник
Прямоугольник, если его противоположные стороны равны, а диагонали равны.
Параллелограмм, но не прямоугольник, если его противоположные стороны равны, а диагонали не равны.
Квадрат, если все стороны равны, а диагонали равны.
Ромб, но не квадрат, если все стороны равны, а диагонали не равны.
Уравнение оси х равно y = 0.
Уравнение оси y равно x = 0.
Уравнение прямой, параллельной оси y на расстоянии a от нее, равно x = a.
Уравнение прямой, параллельной оси x на расстоянии b от нее, равно y = b.
Уравнение прямой, проходящей через точки A (x 1 , y 1 ) и B (x 2 , y 2 ), равно yy 1 / xx 1 = y 2 -y 1 / x 2 -x 1 . Отклонение такой линии равно y 2 -y 1 / x 2 -x 1 .
Уравнение линии в форме пересекающегося наклона Y = mx + c, где m — ее наклон.