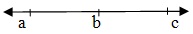Способность — Геометрия

Точка — это точное местоположение

Отрезок

Прямой путь между двумя точками A и B называется отрезком AB. Линейный сегмент имеет две конечные точки.

луч

Продолжая отрезок AB бесконечно в одном направлении, мы получаем луч AB. Луч АБ имеет одну конечную точку, а именно А.

ЛИНИЯ

Линейный отрезок AB, продолжающийся бесконечно в обоих направлениях, называется линией AB.

1. Линия содержит бесконечно много точек.

2. Через заданные точки можно провести бесконечно много линий.

3. Можно провести одну и только одну линию, чтобы пройти через две заданные точки A и B.

4. Две линии встречаются в одной точке.

5. Два самолета встречаются в линию.

Линия содержит бесконечно много точек.

Через заданные точки можно провести бесконечно много линий.

Можно провести одну и только одну линию, чтобы пройти через две заданные точки A и B.

Две линии встречаются в одной точке.

Два самолета встречаются в линию.

Коллинеарная

На данном рисунке точки A, B, C коллинеарны.

Параллельные линии

Три или более линий, пересекающихся в одних и тех же точках, называются параллельными линиями.

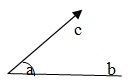
Угол

Два луча OA и OB, имеющие общие конечные точки O, образуют угол AOB, обозначаемый как ∠AOB

Мера угла

Степень превращения из ОА в ОВ называется мерой ∠AOB, записанной как m (∠AOB).

Угол 360 °

Если луч ОА, исходящий из своего исходного положения ОА, вращается вокруг О в направлении против часовой стрелки и после полного вращения возвращается в исходное положение, то мы говорим, что он повернулся на 360. Это полное вращение делится на равные части на 360 °. Тогда каждая часть называется 1 градусом, записанным как 1 °

1 ° = 60 минут, написано как 60 ‘

1 минута = 60 секунд, записанная как 60 «

Типы углов

1. Прямой угол — угол, мера которого составляет 90 °, называется прямым углом.

2. Острый угол — угол, мера которого меньше 90 °, называется острым углом.

3. Угол затупления — Угол, мера которого больше 90 °, но меньше 180 °, называется углом затупления.

4. Прямой угол — угол, мера которого составляет 180 °, называется прямым углом.

5. Угол отражения — угол, мера которого больше 180 °, но меньше 360 °, называется углом отражения.

6. Полный угол — угол, мера которого составляет 360 °, называется полным углом.

7. Равный угол — два угла называются равными, если они имеют одинаковую меру.

8. Дополнительный угол Два угла называются дополнительными, если сумма их измерений равна 90. Например, углы, измеряющие 65 ° и 25 °, являются дополнительным углом.

9. Дополнительный угол — два угла называются дополнительными, если сумма их измерений равна 180 °. Например, углы меры 70 ° и 110 ° являются дополнительными.

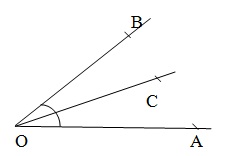
10. Смежный угол — два угла называются смежным углом, если они имеют одну и ту же вершину и общую руку, так что необычные руки находятся по обе стороны от обычной руки. На данном рисунке ∠AOC и ∠BOC — смежный угол.

    

Прямой угол — угол, мера которого составляет 90 °, называется прямым углом.

Острый угол — угол, мера которого меньше 90 °, называется острым углом.

Угол затупления — Угол, мера которого больше 90 °, но меньше 180 °, называется углом затупления.

Прямой угол — угол, мера которого составляет 180 °, называется прямым углом.

Угол отражения — угол, мера которого больше 180 °, но меньше 360 °, называется углом отражения.

Полный угол — угол, мера которого составляет 360 °, называется полным углом.

Равный угол — два угла называются равными, если они имеют одинаковую меру.

Дополнительный угол Два угла называются дополнительными, если сумма их измерений равна 90. Например, углы, измеряющие 65 ° и 25 °, являются дополнительным углом.

Дополнительный угол — два угла называются дополнительными, если сумма их измерений равна 180 °. Например, углы меры 70 ° и 110 ° являются дополнительными.

Смежный угол — два угла называются смежным углом, если они имеют одну и ту же вершину и общую руку, так что необычные руки находятся по обе стороны от обычной руки. На данном рисунке ∠AOC и ∠BOC — смежный угол.

Важные результаты

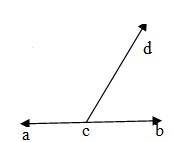
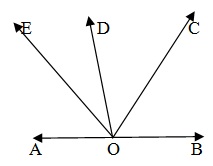
Если луч стоит на линии, то сумма двух смежных углов, образованных таким образом, составляет 180 °. На данном рисунке луч СР стоит на линии AB.

  ∠ ∠ACD + ∠BCD = 180 °. 
     

∠ ∠ACD + ∠BCD = 180 °.

Сумма всех углов, образованных на одной и той же стороне линии в данной точке линии, составляет 180 °. На данном рисунке четыре угла сформированы с одной и той же стороны AOB.

   
  ∠ ∠AOE + ∠EOD + ∠DOC + ∠COD = 180 °. 
  

∠ ∠AOE + ∠EOD + ∠DOC + ∠COD = 180 °.

Сумма всех углов вокруг точки равна 360 °. На данном рисунке пять углов сформированы вокруг точки О.

  ∴∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360 °. 
  

∴∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360 °.

Вертикально противоположные углы

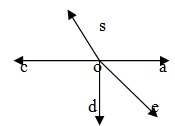
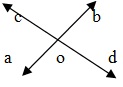
Если две линии A Band CD пересекаются в точке O, то AOC, BOD и BOC, AOD — это две пары вертикально противоположных углов. Вертикально противоположные углы всегда равны.

  ∴ ∠AOC = ∠BOD и ∠AOD = ∠BOC 

∴ ∠AOC = ∠BOD и ∠AOD = ∠BOC

Параллельные линии

Если две линии лежат в одной плоскости и не пересекаются при создании с обеих сторон, то такие линии называются параллельными, и мы пишем L || m.

Линия прорезания параллельных линий

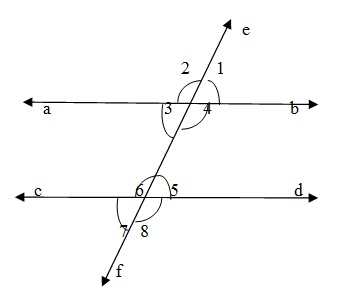
Пусть две параллельные прямые AB и CD разрезаны поперечной EF. затем

Соответствующие углы равны

 (∠1 = ∠5), (∠4 = ∠8), (∠2 = ∠6), (∠3 = ∠7)

Альтернативные внутренние углы равны.

 (∠3 = ∠5) и (∠4 = ∠6)

Внутренние углы являются дополнительными

 +4 + ∠5 = 180 ° и ∠3 + ∠6 = 180 °.                                               

Треугольник

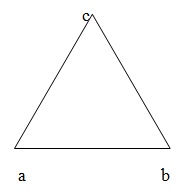
Фигура, ограниченная тремя прямыми линиями, называется треугольником. На данном рисунке мы имеем ∆ABC; ∆ABC, имеющий три вершины A, B, C. В имеет три угла, а именно ∠A, ∠B и ∠C. Он имеет три стороны, а именно AB, AC и BC.

Типы треугольника

1. Треугольник, у которого все стороны равны, называется равносторонним треугольником.

2. Треугольник, имеющий две равные стороны, называется равнобедренным треугольником.

3. Треугольник, имеющий все стороны разной длины, называется разносторонним треугольником.

4. Треугольник, один из углов которого составляет 90 °, называется прямоугольным треугольником.

5. Треугольник, один из углов которого лежит между 90 ° и 180 °, называется тупым треугольником.

6. Треугольник, каждый угол которого острый, называется острым треугольником.

7. Сумма всех сторон треугольника называется периметром треугольника.

8. Сумма двух сторон треугольника больше третьей стороны.

9. В прямоугольном ABC, в котором ∠B = 90 °, AC ² = AB ² + BC ² . Это называется теорема Пифагора.

Треугольник, у которого все стороны равны, называется равносторонним треугольником.

Треугольник, имеющий две равные стороны, называется равнобедренным треугольником.

Треугольник, имеющий все стороны разной длины, называется разносторонним треугольником.

Треугольник, один из углов которого составляет 90 °, называется прямоугольным треугольником.

Треугольник, один из углов которого лежит между 90 ° и 180 °, называется тупым треугольником.

Треугольник, каждый угол которого острый, называется острым треугольником.

Сумма всех сторон треугольника называется периметром треугольника.

Сумма двух сторон треугольника больше третьей стороны.

В прямоугольном ABC, в котором ∠B = 90 °, AC ² = AB ² + BC ² . Это называется теорема Пифагора.

четырехугольник

Фигура, ограниченная четырьмя прямыми, называется четырехугольником. Сумма всех углов четырехугольника составляет 360 °.

Прямоугольник — четырехугольник называется прямоугольником, если его противоположные стороны равны и каждый его угол равен 90 °. На данном рис. ABCD это прямоугольник.

Квадрат — четырехугольник называется квадратом, если все его стороны равны и каждый из его углов составляет 90 °. На данном рис. ABCD — это квадрат, в котором AB = BC = CD = DA.

Параллелограмм — четырехугольник называется параллелограммом, если его противоположные стороны параллельны. На данном рис. ABCD — это параллелограмм, в котором AB = DC и AD = BC.

Ромб — параллелограмм, имеющий все равные стороны, называется ромбом. На данном рис. ABCD — это ромб, в котором AB = BC = CD = DA, AB || DC и AD || ДО НАШЕЙ ЭРЫ.

Четырехугольник — это прямоугольник, если противоположные стороны равны, а его диагонали равны.

Четырехугольник — это квадрат, если все стороны равны, а диагональ одинакова.

Четырехугольник — это параллелограмм, если противоположные стороны равны.

Четырехугольник — это параллелограмм, но не прямоугольник, если противоположные стороны равны, но диагонали не равны.

Четырехугольник — это ромб, но не квадрат, если все их стороны равны, а диагонали не равны.

В параллелограмме мы имеем

Противоположные стороны равны.

Противоположные углы равны.

Каждая диагональ делит параллелограмм на две части.

Диагонали параллелограмма делят пополам друг на друга.

Диагонали прямоугольника равны.

Диагонали ромба делят пополам друг на друга под прямым углом.

Перпендикуляр от центра к аккорду делит аккорд.

Один и только один круг проходит через три неколлинеарных точки.

Угол в полукруге — это прямой угол.

Противоположные углы циклического четырехугольника являются дополнительными.

Угол в том же сегменте круга равен.

Касательная в любой точке окружности перпендикулярна радиусу через точку контакта.

Два касательных к окружности из точки за ее пределами равны.

Если PT является касательной к окружности, а PAB является секущей, то PA x PB = PT ²