Цифровые схемы — метод K-Map

В предыдущих главах мы упростили булевы функции, используя булевы постулаты и теоремы. Это трудоемкий процесс, и мы должны переписывать упрощенные выражения после каждого шага.

Чтобы преодолеть эту трудность, Карно ввел метод упрощения булевых функций простым способом. Этот метод известен как метод карты Карно или метод K-карты. Это графический метод, который состоит из 2 ⁿ ячеек для n переменных. Соседние ячейки отличаются только позицией одного бита.

K-Maps для 2-5 переменных

Метод K-Map наиболее подходит для минимизации булевых функций от 2 переменных до 5 переменных. Теперь давайте поговорим о K-Maps для 2-5 переменных одна за другой.

2 Переменная K-Map

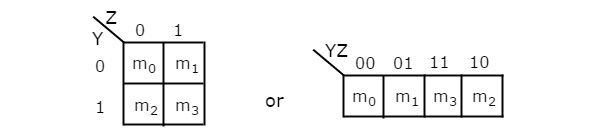
Количество ячеек в 2-х переменных K-map равно четырем, поскольку количество переменных равно двум. На следующем рисунке показаны 2 переменные K-Map .

• Существует только одна возможность группировки 4 смежных минимальных терминов.

• Возможные комбинации группировки 2 смежных минимальных терминов: {(m ₀ , m ₁ ), (m ₂ , m ₃ ), (m ₀ , m ₂ ) и (m ₁ , m ₃ )}.

Существует только одна возможность группировки 4 смежных минимальных терминов.

Возможные комбинации группировки 2 смежных минимальных терминов: {(m ₀ , m ₁ ), (m ₂ , m ₃ ), (m ₀ , m ₂ ) и (m ₁ , m ₃ )}.

3 Переменная K-карта

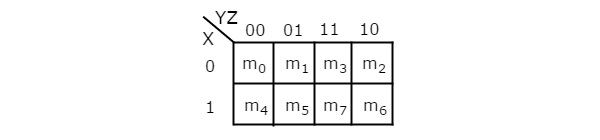
Количество ячеек в 3-х переменных K-map равно восьми, поскольку количество переменных равно трем. На следующем рисунке показаны 3 переменные K-Map .

• Существует только одна возможность группировки 8 смежных минимальных терминов.

• Возможные комбинации группировки 4 смежных минимальных терминов: {(m ₀ , m ₁ , m ₃ , m ₂ ), (m ₄ , m ₅ , m ₇ , m ₆ ), (m ₀ , m ₁ , m ₄ , m ₅ ), (м ₁ , м ₃ , м ₅ , м ₇ ), (м ₃ , м ₂ , м ₇ , м ₆ ) и (м ₂ , м ₀ , м ₆ , м ₄ )}.

• Возможные комбинации группировки 2 смежных минимальных терминов: {(m ₀ , m ₁ ), (m ₁ , m ₃ ), (m ₃ , m ₂ ), (m ₂ , m ₀ ), (m ₄ , m ₅ ) , (м ₅ , м ₇ ), (м ₇ , м ₆ ), (м ₆ , м ₄ ), (м ₀ , м ₄ ), (м ₁ , м ₅ ), (м ₃ , м ₇ ) и ( м ₂ , м ₆ )}.

• Если x = 0, то 3-х переменная K-карта становится 2-х переменной K-map.

Существует только одна возможность группировки 8 смежных минимальных терминов.

Возможные комбинации группировки 4 смежных минимальных терминов: {(m ₀ , m ₁ , m ₃ , m ₂ ), (m ₄ , m ₅ , m ₇ , m ₆ ), (m ₀ , m ₁ , m ₄ , m ₅ ), (м ₁ , м ₃ , м ₅ , м ₇ ), (м ₃ , м ₂ , м ₇ , м ₆ ) и (м ₂ , м ₀ , м ₆ , м ₄ )}.

Возможные комбинации группировки 2 смежных минимальных терминов: {(m ₀ , m ₁ ), (m ₁ , m ₃ ), (m ₃ , m ₂ ), (m ₂ , m ₀ ), (m ₄ , m ₅ ) , (м ₅ , м ₇ ), (м ₇ , м ₆ ), (м ₆ , м ₄ ), (м ₀ , м ₄ ), (м ₁ , м ₅ ), (м ₃ , м ₇ ) и ( м ₂ , м ₆ )}.

Если x = 0, то 3-х переменная K-карта становится 2-х переменной K-map.

4 Переменная K-Map

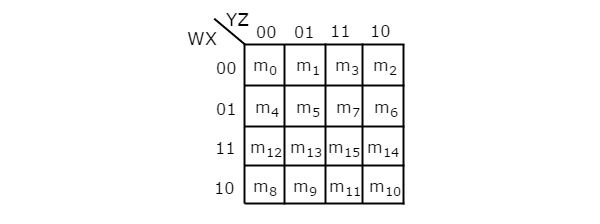
Количество ячеек в 4-х переменных K-map равно шестнадцати, поскольку количество переменных равно четырем. На следующем рисунке показано 4 переменных K-Map .

• Существует только одна возможность группировки 16 смежных минимальных терминов.

• Пусть R ₁ , R ₂ , R ₃ и R ₄ представляют минимальные члены первого ряда, второго ряда, третьего ряда и четвертого ряда соответственно. Аналогично, C ₁ , C ₂ , C ₃ и C ₄ представляют минимальные термины первого столбца, второго столбца, третьего столбца и четвертого столбца соответственно. Возможные комбинации группировки 8 смежных минимальных терминов: {(R ₁ , R ₂ ), (R ₂ , R ₃ ), (R ₃ , R ₄ ), (R ₄ , R ₁ ), (C ₁ , C ₂ ) , (C ₂ , C ₃ ), (C ₃ , C ₄ ), (C ₄ , C ₁ )}.

• Если w = 0, то 4-х переменных K-map становится 3-х переменных K-map.

Существует только одна возможность группировки 16 смежных минимальных терминов.

Пусть R ₁ , R ₂ , R ₃ и R ₄ представляют минимальные члены первого ряда, второго ряда, третьего ряда и четвертого ряда соответственно. Аналогично, C ₁ , C ₂ , C ₃ и C ₄ представляют минимальные термины первого столбца, второго столбца, третьего столбца и четвертого столбца соответственно. Возможные комбинации группировки 8 смежных минимальных терминов: {(R ₁ , R ₂ ), (R ₂ , R ₃ ), (R ₃ , R ₄ ), (R ₄ , R ₁ ), (C ₁ , C ₂ ) , (C ₂ , C ₃ ), (C ₃ , C ₄ ), (C ₄ , C ₁ )}.

Если w = 0, то 4-х переменных K-map становится 3-х переменных K-map.

5 переменных K-Map

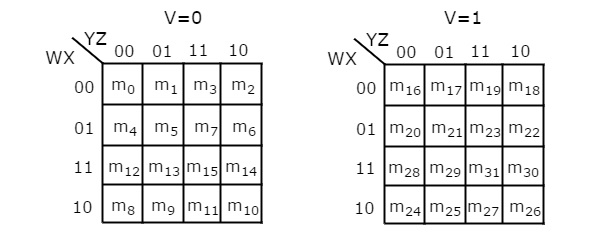
Количество ячеек в 5-переменной переменной K-map равно тридцати двум, поскольку количество переменных равно 5. На следующем рисунке показана 5-переменная K-Map .

• Существует только одна возможность группировки 32 смежных минимальных терминов.

• Есть две возможности группировки 16 смежных минимальных терминов. то есть группировка минимальных членов от m ₀ до m ₁₅ и от m ₁₆ до m ₃₁ .

• Если v = 0, то 5 переменных K-map становятся 4 переменными K-map.

Существует только одна возможность группировки 32 смежных минимальных терминов.

Есть две возможности группировки 16 смежных минимальных терминов. то есть группировка минимальных членов от m ₀ до m ₁₅ и от m ₁₆ до m ₃₁ .

Если v = 0, то 5 переменных K-map становятся 4 переменными K-map.

В вышеупомянутых всех K-картах мы использовали исключительно обозначение минимальных терминов. Точно так же вы можете использовать исключительно обозначение Макс. Терминов.

Минимизация булевых функций с использованием K-Maps

Если мы рассмотрим комбинацию входных данных, для которых булева функция равна ‘1’, то мы получим булеву функцию, которая находится в стандартной сумме форм продуктов после упрощения K-карты.

Точно так же, если мы рассмотрим комбинацию входов, для которых булева функция равна ‘0’, то мы получим булеву функцию, которая находится в стандартном произведении формы сумм после упрощения K-карты.

Следуйте этим правилам для упрощения K-карт , чтобы получить стандартную сумму продуктов формы.

• Выберите соответствующую K-карту в зависимости от количества переменных, присутствующих в булевой функции.

• Если булева функция задана в виде суммы минимальных членов, поместите их в соответствующие ячейки минимальных членов на K-карте. Если булева функция задана в виде суммы произведений, поместите их во все возможные ячейки K-карты, для которых действительны заданные условия произведений.

• Проверьте возможности группировки максимального количества смежных. Это должно быть полномочия двух. Начните с максимальной степени двух и до минимальной степени двух. Наибольшая мощность равна числу переменных, рассматриваемых в K-карте, а наименьшая мощность равна нулю.

• Каждая группа будет давать буквальный или один товарный термин. Это известно как главный импликант . Первичный импликант называется существенным первичным импликантом , если хотя бы один «1» не охватывается какими-либо другими группировками, а охватывает только эта группировка.

• Запишите все основные и важные основные факторы. Упрощенная булева функция содержит все основные простые импликанты и только необходимые простые импликанты.

Выберите соответствующую K-карту в зависимости от количества переменных, присутствующих в булевой функции.

Если булева функция задана в виде суммы минимальных членов, поместите их в соответствующие ячейки минимальных членов на K-карте. Если булева функция задана в виде суммы произведений, поместите их во все возможные ячейки K-карты, для которых действительны заданные условия произведений.

Проверьте возможности группировки максимального количества смежных. Это должно быть полномочия двух. Начните с максимальной степени двух и до минимальной степени двух. Наибольшая мощность равна числу переменных, рассматриваемых в K-карте, а наименьшая мощность равна нулю.

Каждая группа будет давать буквальный или один товарный термин. Это известно как главный импликант . Первичный импликант называется существенным первичным импликантом , если хотя бы один «1» не охватывается какими-либо другими группировками, а охватывает только эта группировка.

Запишите все основные и важные основные факторы. Упрощенная булева функция содержит все основные простые импликанты и только необходимые простые импликанты.

Примечание 1 — Если выходы не определены для некоторой комбинации входов, то эти выходные значения будут представлены символом «x» . Это означает, что мы можем рассматривать их как «0» или «1».

Примечание 2 — Если не нужны термины, присутствующие также, тогда не обращайте внимания на ‘x’ в соответствующих ячейках K-карты. Рассмотрим только те «x», которые не важны для группирования максимального числа соседних. В этих случаях рассматривайте значение «все равно» как «1».

пример

Упростим следующую булеву функцию f (W, X, Y, Z) = WX’Y ‘+ WY + W’YZ’, используя K-map.

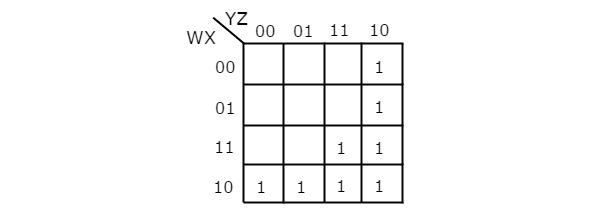
Данная булева функция находится в виде суммы произведений. Он имеет 4 переменные W, X, Y и Z. Итак, нам требуется 4 переменных K-map . K-карта с четырьмя переменными , соответствующая заданным условиям продукта, показана на следующем рисунке.

Здесь 1s помещены в следующие ячейки K-карты.

• Ячейки, которые являются общими для пересечения строки 4 и столбцов 1 и 2, соответствуют термину продукта WX’Y ‘ .

• Ячейки, которые являются общими для пересечения строк 3 и 4 и столбцов 3 и 4, соответствуют термину продукта WY .

• Ячейки, которые являются общими для пересечения строк 1 и 2 и столбца 4, соответствуют термину продукта W’YZ ‘ .

Ячейки, которые являются общими для пересечения строки 4 и столбцов 1 и 2, соответствуют термину продукта WX’Y ‘ .

Ячейки, которые являются общими для пересечения строк 3 и 4 и столбцов 3 и 4, соответствуют термину продукта WY .

Ячейки, которые являются общими для пересечения строк 1 и 2 и столбца 4, соответствуют термину продукта W’YZ ‘ .

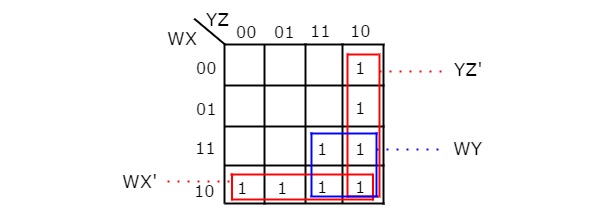
Нет возможности сгруппировать 16 соседних или 8 соседних. Есть три возможности группировки 4 смежных. После этих трех группировок не останется ни одной группы. Таким образом, нам не нужно проверять для группировки 2 смежных. K-карта с четырьмя переменными с этими тремя группировками показана на следующем рисунке.

Здесь мы получили три главных импликанта WX ‘, WY & YZ’. Все эти основные факторы важны по следующим причинам.

• Два из них (m ₈ и m ₉ ) из группы четвертого ряда не охватываются никакими другими группами. Только четвертая группа строк охватывает эти два.

• Одиночная (м ₁₅ ) группа квадратной формы не охватывается никакими другими группами. Только группировка квадратной формы покрывает это.

• Два (m ₂ & m ₆ ) четвертой группы столбцов не охватываются никакими другими группами. Только четвертая группа столбцов охватывает эти два.

Два из них (m ₈ и m ₉ ) из группы четвертого ряда не охватываются никакими другими группами. Только четвертая группа строк охватывает эти два.

Одиночная (м ₁₅ ) группа квадратной формы не охватывается никакими другими группами. Только группировка квадратной формы покрывает это.

Два (m ₂ & m ₆ ) четвертой группы столбцов не охватываются никакими другими группами. Только четвертая группа столбцов охватывает эти два.

Следовательно, упрощенная булева функция

f = WX ‘+ WY + YZ’

Следуйте этим правилам для упрощения K-карт , чтобы получить стандартный продукт формы сумм.

• Выберите соответствующую K-карту в зависимости от количества переменных, присутствующих в булевой функции.

• Если булева функция задана как произведение формы максимальных членов, поместите нули в соответствующие ячейки максимальных членов на K-карте. Если булева функция задана как произведение суммы суммы, то поместите нули во все возможные ячейки K-карты, для которых действительны заданные суммы сумм.

• Проверьте возможности группировки максимального количества соседних нулей. Это должно быть полномочия двух. Начните с максимальной степени двух и до минимальной степени двух. Наибольшая мощность равна числу переменных, рассматриваемых в K-карте, а наименьшая мощность равна нулю.

• Каждая группировка будет давать буквальное или однозначное выражение. Это известно как главный импликант . Первичный импликант называется существенным первичным импликантом , если хотя бы один «0» не покрывается какими-либо другими группировками, а охватывает только эта группировка.

• Запишите все основные и важные основные факторы. Упрощенная булева функция содержит все основные простые импликанты и только необходимые простые импликанты.

Выберите соответствующую K-карту в зависимости от количества переменных, присутствующих в булевой функции.

Если булева функция задана как произведение формы максимальных членов, поместите нули в соответствующие ячейки максимальных членов на K-карте. Если булева функция задана как произведение суммы суммы, то поместите нули во все возможные ячейки K-карты, для которых действительны заданные суммы сумм.

Проверьте возможности группировки максимального количества соседних нулей. Это должно быть полномочия двух. Начните с максимальной степени двух и до минимальной степени двух. Наибольшая мощность равна числу переменных, рассматриваемых в K-карте, а наименьшая мощность равна нулю.

Каждая группировка будет давать буквальное или однозначное выражение. Это известно как главный импликант . Первичный импликант называется существенным первичным импликантом , если хотя бы один «0» не покрывается какими-либо другими группировками, а охватывает только эта группировка.

Запишите все основные и важные основные факторы. Упрощенная булева функция содержит все основные простые импликанты и только необходимые простые импликанты.

Примечание. Если не имеют значения термины, присутствующие, тогда не обращайте внимания на ‘x’ в соответствующих ячейках K-карты. Рассмотрим только те значения x, которые полезны для группировки максимального количества смежных нулей. В этих случаях обрабатывайте значение «все равно» как «0».

пример

Упростим следующую булеву функцию: $f \ left (X, Y, Z \ right) = \ prod M \ left (0,1,2,4 \ right)$, используя K-map.

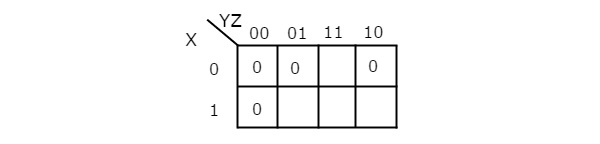
Данная булева функция находится в произведении формы Макса. Он имеет 3 переменные X, Y & Z. Итак, нам требуется 3 переменных K-map. Данные условия Max: M ₀ , M ₁ , M ₂ и M ₄ . 3-х переменная K-карта с нулями, соответствующими заданным условиям Max, показана на следующем рисунке.

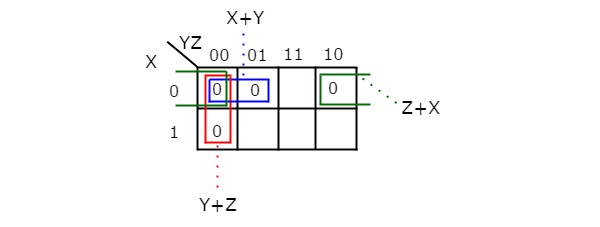
Нет возможности сгруппировать 8 смежных нулей или 4 смежных нуля. Существует три возможности группировки 2 смежных нулей. После этих трех группировок не остается ни одного нулевого разгруппированного. K-карта с тремя переменными с этими тремя группировками показана на следующем рисунке.

Здесь мы получили три простых импликанта X + Y, Y + Z и Z + X. Все эти простые импликанты существенны, потому что один ноль в каждой группировке не охватывается никакими другими группировками, за исключением их отдельных группировок.

Следовательно, упрощенная булева функция

f = (X + Y). (Y + Z). (Z + X)

Таким образом, мы можем легко упростить булевы функции до 5 переменных, используя метод K-map. Для более чем 5 переменных сложно упростить функции с помощью K-Maps. Потому что количество ячеек в K-карте удваивается за счет включения новой переменной.

Из-за этого проверка и группировка смежных (минимальные условия) или смежных нулей (максимальные условия) будут затруднены. Мы обсудим метод Tabular в следующей главе, чтобы преодолеть трудности метода K-map.