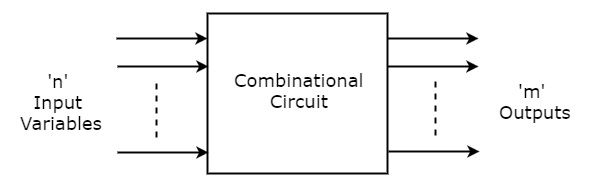
Комбинационные схемы состоят из логических элементов. Эти схемы работают с двоичными значениями. Выход (ы) комбинационной схемы зависит от комбинации имеющихся входов. На следующем рисунке показана блок-схема комбинационной схемы.
Эта комбинационная схема имеет n входных переменных и m выходов. Каждая комбинация входных переменных будет влиять на выходные данные.
Методика расчета комбинационных цепей
-
Найдите требуемое количество входных переменных и выходов из заданных спецификаций.
-
Сформулируйте таблицу Истины . Если есть n входных переменных, то будет 2n возможных комбинаций. Для каждой комбинации входных данных найдите выходные значения.
-
Найдите логические выражения для каждого вывода. При необходимости упростите эти выражения.
-
Реализуйте вышеупомянутые логические выражения, соответствующие каждому выводу, используя логические элементы .
Найдите требуемое количество входных переменных и выходов из заданных спецификаций.
Сформулируйте таблицу Истины . Если есть n входных переменных, то будет 2n возможных комбинаций. Для каждой комбинации входных данных найдите выходные значения.
Найдите логические выражения для каждого вывода. При необходимости упростите эти выражения.
Реализуйте вышеупомянутые логические выражения, соответствующие каждому выводу, используя логические элементы .
Преобразователи кода
Мы обсудили различные коды в главе под названием коды. Преобразователи, которые преобразуют один код в другой, называются преобразователями кода . Эти преобразователи кода в основном состоят из логических элементов.
пример
Конвертер двоичного кода в код Грея
Давайте реализуем конвертер, который преобразует 4-битный двоичный код WXYZ в его эквивалентный код Грея ABCD.
В следующей таблице показана таблица истинности 4-разрядного двоичного кода в преобразователь кода Грея.
| Двоичный код WXYZ | WXYZ Серый код ABCD |
|---|---|
| 0000 | 0000 |
| 0001 | 0001 |
| 0010 | 0011 |
| 0011 | 0010 |
| 0100 | 0110 |
| 0101 | 0111 |
| 0110 | 0101 |
| 0111 | 0100 |
| 1000 | 1100 |
| 1001 | 1101 |
| 1010 | 1111 |
| 1011 | 1110 |
| 1100 | 1010 |
| 1101 | 1011 |
| 1110 | 1001 |
| 1111 | 1000 |
Из таблицы Truth мы можем записать логические функции для каждого выходного бита кода Грея, как показано ниже.
$$ A = \ sum m \ left (8,9,10,11,12,13,14,15 \ right) $$
$$ B = \ sum m \ left (4,5,6,7,8,9,10,11 \ right) $$
$$ C = \ sum m \ left (2,3,4,5,10,11,12,13 \ right) $$
$$ D = \ sum m \ left (1,2,5,6,9,10,13,14 \ right) $$
Упростим перечисленные выше функции, используя 4 переменные K-Maps.
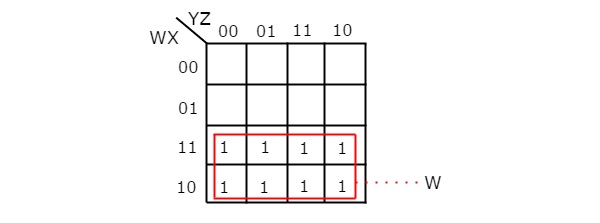
На следующем рисунке показана 4-х переменная K-Map для упрощения булевой функции A.
Сгруппировав 8 смежных, мы получили $ A = W $.
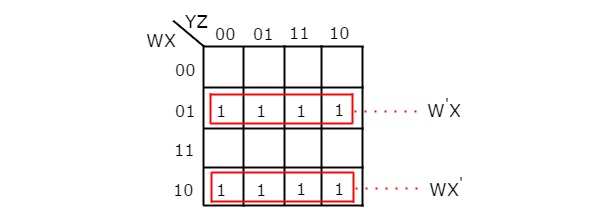
На следующем рисунке показана 4-переменная K-Map для упрощения булевой функции B.
Есть две группы из 4 смежных. После группировки мы получим B как
$$ B = {W} ‘X + W {X}’ = W \ oplus X $$
Точно так же мы получим следующие логические функции для C & D после упрощения.
$$ C = {X} ‘Y + X {Y}’ = X \ oplus Y $$
$$ D = {Y} ‘Z + Y {Z}’ = Y \ oplus Z $$
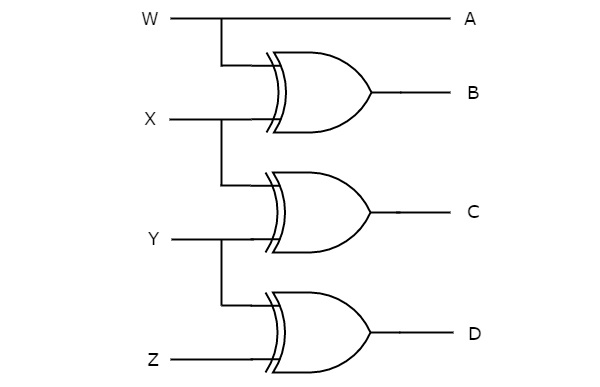
На следующем рисунке показана принципиальная схема преобразователя 4-битного двоичного кода в код Грея.
Поскольку выходы зависят только от существующих входов, этот 4-битный преобразователь двоичного кода в код Грея является комбинационной схемой. Точно так же вы можете реализовать другие конвертеры кода.
Генератор четности
Существует два типа генераторов битов четности, основанных на типе генерируемого бита четности. Даже генератор четности генерирует бит четности. Аналогично, генератор нечетной четности генерирует бит нечетной четности.
Четный генератор четности
Теперь давайте реализуем четный генератор четности для 3-битного двоичного входа WXY. Он генерирует четный бит четности P. Если на входе присутствует нечетное число единиц, то четный бит четности P должен быть равен 1, чтобы результирующее слово содержало четное число единиц. Для других комбинаций ввода, даже четного бита, P должно быть ‘0’. В следующей таблице показана таблица истинности генератора четности.
| Двоичный вход WXY | Четный бит P |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 1 |
| 011 | 0 |
| 100 | 1 |
| 101 | 0 |
| 110 | 0 |
| 111 | 1 |
Из приведенной выше таблицы истинности мы можем записать логическую функцию для четного бита как
$$ P = {W} ‘{X}’ Y + {W} ‘Х {У}’ + W {X} {Y} ‘+ WXY $$
$ \ Rightarrow P = {W} ‘\ left ({X}’ Y + X {Y} ‘\ right) + W \ left ({X}’ {Y} ‘+ XY \ right) $
$ \ Rightarrow P = {W} ‘\ left (X \ oplus Y \ right) + W {\ left (X \ oplus Y \ right)}’ = W \ oplus X \ oplus Y $
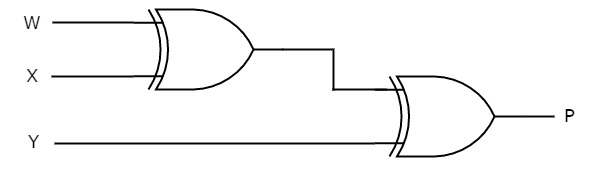
На следующем рисунке показана принципиальная схема четного генератора четности.
Эта схема состоит из двух вентилей типа « исключающее ИЛИ» , каждый из которых имеет два входа. Первый вентиль ExclusiveOR имеет два входа W & X и выдает выход W ⊕ X. Этот выход задается как один вход второго вентиля Exclusive-OR. Другим входом этого второго логического элемента «Исключающее ИЛИ» является Y, который выдает выход W ⊕ X ⊕ Y.
Генератор нечетных четностей
Если на входе присутствует четное число единиц, то нечетный бит четности, P должен быть равен 1, чтобы результирующее слово содержало нечетное число единиц. Для других комбинаций ввода, нечетного бита четности, P должно быть ‘0’.
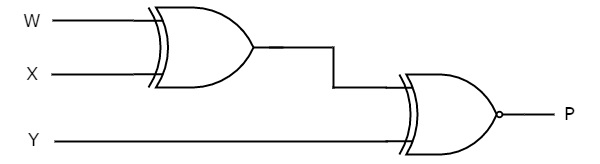
Выполните ту же процедуру генератора четности для реализации генератора нечетности. Принципиальная схема генератора нечетной четности показана на следующем рисунке.
Вышеприведенная принципиальная схема состоит из шлюза Ex-OR на первом уровне и шлюза Ex-NOR на втором уровне. Поскольку нечетная четность прямо противоположна четной четности, мы можем разместить инвертор на выходе генератора четной четности. В этом случае первый и второй уровни содержат вентиль ExOR на каждом уровне, а третий уровень состоит из инвертора.
Проверка четности
Существует два типа проверок четности в зависимости от типа проверяемой четности. Четная проверка четности проверяет ошибку в передаваемых данных, которые содержат биты сообщения наряду с четной четностью. Аналогичным образом, проверка нечетной четности проверяет ошибку в передаваемых данных, которая содержит биты сообщения наряду с нечетной четностью.
Четный паритет
Теперь давайте реализуем схему проверки четности. Предположим, что 3-битный двоичный вход передает WXY вместе с четным битом четности P. Таким образом, результирующее слово (данные) содержит 4 бита, которые будут получены в качестве входных данных проверки четности.
Он генерирует четный бит проверки четности, E. Этот бит будет нулевым, если полученные данные содержат четное количество единиц. Это означает, что в полученных данных нет ошибок. Этот бит проверки четности будет равен единице, если полученные данные содержат нечетное число единиц. Это означает, что в полученных данных произошла ошибка.
В следующей таблице показана таблица истинности проверки четности.
| 4-битные полученные данные WXYP | Четный контроль четности, бит E |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 1 |
| 0011 | 0 |
| 0100 | 1 |
| 0101 | 0 |
| 0110 | 0 |
| 0111 | 1 |
| 1000 | 1 |
| 1001 | 0 |
| 1010 | 0 |
| 1011 | 1 |
| 1100 | 0 |
| 1101 | 1 |
| 1110 | 1 |
| 1111 | 0 |
Из приведенной выше таблицы истинности мы можем заметить, что значение бита для проверки четности равно ‘1’, когда в полученных данных присутствует нечетное число единиц. Это означает, что булева функция бита проверки четности является нечетной функцией . Функция Exclusive-OR удовлетворяет этому условию. Следовательно, мы можем напрямую записать булеву функцию четного бита проверки четности как
$$ E = W \ oplus X \ oplus Y \ oplus P $$
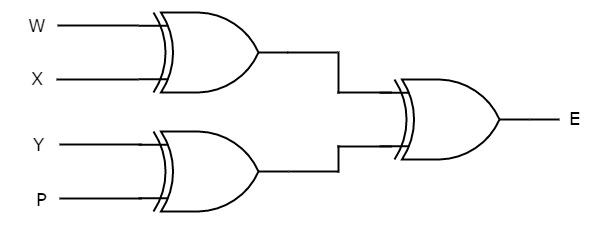
На следующем рисунке показана принципиальная схема проверки четности.
Эта схема состоит из трех вентилей типа « исключающее ИЛИ» , каждый из которых имеет два входа. Ворота первого уровня выдают выходные данные $ W \ oplus X $ & $ Y \ oplus P $. Вентиль Exclusive-OR, который находится на втором уровне, производит вывод $ W \ oplus X \ oplus Y \ oplus P $
Проверка нечетности
Предположим, что 3-битный двоичный вход передает WXY вместе с нечетным битом четности P. Таким образом, результирующее слово (данные) содержит 4 бита, которые будут получены в качестве входных данных проверки нечетной четности.
Он генерирует нечетный бит проверки четности, E. Этот бит будет нулевым, если полученные данные содержат нечетное количество единиц. Это означает, что в полученных данных нет ошибок. Этот бит нечетной проверки на четность будет равен единице, если полученные данные содержат четное количество единиц. Это означает, что в полученных данных произошла ошибка.
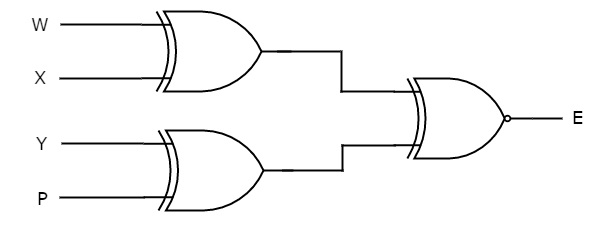
Выполните ту же процедуру проверки четности для реализации проверки нечетности. Принципиальная электрическая схема нечетного контроля четности показана на следующем рисунке.
Вышеприведенная принципиальная схема состоит из вентилей Ex-OR на первом уровне и вентиля Ex-NOR на втором уровне. Поскольку нечетная четность прямо противоположна четной четности, мы можем разместить инвертор на выходе проверки четности. В этом случае первый, второй и третий уровни содержат два вентиля Ex-OR, один вентиль Ex-OR и один инвертор соответственно.