Оптимизация с использованием Hopfield Network

Оптимизация — это действие, направленное на то, чтобы сделать что-то вроде дизайна, ситуации, ресурса и системы как можно более эффективным. Используя сходство между функцией стоимости и функцией энергии, мы можем использовать сильно взаимосвязанные нейроны для решения задач оптимизации. Такой вид нейронной сети представляет собой сеть Хопфилда, которая состоит из одного слоя, содержащего один или несколько полностью связанных рекуррентных нейронов. Это может быть использовано для оптимизации.

Что нужно помнить при использовании сети Hopfield для оптимизации —

• Энергетическая функция должна быть минимальной в сети.

• Он найдет удовлетворительное решение, а не выберет один из сохраненных шаблонов.

• Качество решения, найденного сетью Хопфилда, существенно зависит от начального состояния сети.

Энергетическая функция должна быть минимальной в сети.

Он найдет удовлетворительное решение, а не выберет один из сохраненных шаблонов.

Качество решения, найденного сетью Хопфилда, существенно зависит от начального состояния сети.

Задача коммивояжера

Поиск кратчайшего маршрута, пройденного продавцом, является одной из вычислительных проблем, которая может быть оптимизирована с помощью нейронной сети Хопфилда.

Основная концепция TSP

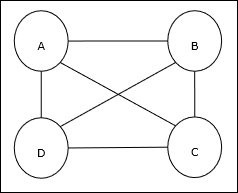
Задача коммивояжера (TSP) — это классическая задача оптимизации, при которой продавец должен путешествовать по n городам, которые связаны друг с другом, сохраняя при этом стоимость и минимальное пройденное расстояние. Например, продавец должен совершить поездку по четырем городам A, B, C, D, и цель состоит в том, чтобы найти кратчайший круговой тур, ABC-D, чтобы минимизировать стоимость, которая также включает в себя стоимость поездки из последний город D до первого города A.

Матричное представление

Фактически, каждый обзор TSP по n-городам может быть выражен в виде матрицы n × n , i- _я строка которой описывает местоположение i- _го города. Эта матрица M для 4 городов A, B, C, D может быть выражена следующим образом:

$$M = \ begin {bmatrix} A: & 1 & 0 & 0 & 0 \\ B: & 0 & 1 & 0 & 0 \\ C: & 0 & 0 & 1 & 0 \\ D: & 0 & 0 & 0 & 1 \ end {bmatrix}$$

Решение от Hopfield Network

При рассмотрении решения этого TSP сетью Хопфилда каждый узел в сети соответствует одному элементу в матрице.

Расчет энергетической функции

Чтобы быть оптимизированным решением, энергетическая функция должна быть минимальной. На основании следующих ограничений мы можем вычислить энергетическую функцию следующим образом:

Constraint-I

Первое ограничение, на основе которого мы будем вычислять энергетическую функцию, состоит в том, что один элемент должен быть равен 1 в каждой строке матрицы M, а другие элементы в каждой строке должны равняться 0, поскольку каждый город может находиться только в одной позиции в TSP тур. Это ограничение можно математически записать следующим образом:

$$ \ displaystyle \ sum \ limit_ {j = 1} ^ n M_ {x, j} \: = \: 1 \: для \: x \: \ in \: \ lbrace1, …, n \ rbrace $ $

Теперь функция энергии, которая должна быть минимизирована, на основе вышеуказанного ограничения, будет содержать член, пропорциональный —

 displaystyle sum limitnx=1 left( beginarrayc1− displaystyle sum limitnj=1Mx,j конецмассива справа)2 $$\ displaystyle \ sum \ limit_ {x = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limit_ {j = 1} ^ n M_ {x, j } \ {конец массива} \ справа) ^ 2$$

Constraint-II

Как мы знаем, в TSP один город может находиться в любой позиции в туре, следовательно, в каждом столбце матрицы M один элемент должен быть равен 1, а другие элементы должны быть равны 0. Это ограничение математически может быть записано следующим образом:

$$ \ displaystyle \ sum \ limit_ {x = 1} ^ n M_ {x, j} \: = \: 1 \: для \: j \: \ in \: \ lbrace1, …, n \ rbrace $ $

Теперь функция энергии, которая должна быть минимизирована, на основе вышеуказанного ограничения, будет содержать член, пропорциональный —

 displaystyle sum limitnj=1 left( beginarrayc1− displaystyle sum limitnx=1Mx,j конецмассива справа)2 $$\ displaystyle \ sum \ limit_ {j = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limit_ {x = 1} ^ n M_ {x, j } \ {конец массива} \ справа) ^ 2$$

Расчет функции стоимости

Предположим, что квадратная матрица ( n × n ), обозначенная буквой C, обозначает матрицу затрат TSP для n городов, где n> 0 . Ниже приведены некоторые параметры при расчете функции стоимости —

• C _{x, y} — Элемент матрицы затрат обозначает стоимость проезда от города x до y .

• Смежность элементов A и B может быть показана следующим соотношением —

C _{x, y} — Элемент матрицы затрат обозначает стоимость проезда от города x до y .

Смежность элементов A и B может быть показана следующим соотношением —

Mx,i=1иMy,i pm1=1 $$M_ {x, i} \: = \: 1 \: \: и \: \: M_ {y, i \ pm 1} \: = \: 1$$

Как мы знаем, в матрице выходное значение каждого узла может быть 0 или 1, следовательно, для каждой пары городов A, B мы можем добавить следующие члены к энергетической функции:

 displaystyle sum limitni=1Cx,yMx,i(My,i+1+My,i−1) $$\ displaystyle \ sum \ limit_ {i = 1} ^ n C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1})$$

На основе вышеуказанной функции стоимости и значения ограничения конечная энергетическая функция E может быть задана следующим образом:

E= frac12 displaystyle sum limitni=1 displaystyle sum limitx displaystyle sum limity neqxCх,уMх,(Mу,+1 +MY,I−1) + $$E \: = \: \ frac {1} {2} \ displaystyle \ sum \ limit_ {i = 1} ^ n \ displaystyle \ sum \ limit_ {x} \ displaystyle \ sum \ limit_ {y \ neq x} C_ {х, у} M_ {х,} (M_ {у, + 1} \ + \: M_ {Y, I-1}) \ +$$

 beginbmatrix gamma1 displaystyle sum limitx left( beginarrayc1− displaystyle sum limitiMx,i endarray right)2+ gamma2 displaystyle sum limiti left( beginarrayc1− : displaystyle sum limitxMx,i endarray right)2 endbmatrix $$\: \ begin {bmatrix} \ gamma_ {1} \ displaystyle \ sum \ limit_ {x} \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limit_ {i} M_ {x, i} \ end {array} \ right) ^ 2 \: + \: \ gamma_ {2} \ displaystyle \ sum \ limit_ {i} \ left (\ begin {array} {c} 1 \: - \ : \ displaystyle \ sum \ limit_ {x} M_ {x, i} \ end {array} \ right) ^ 2 \ end {bmatrix}$$

Здесь γ ₁ и γ ₂ — две постоянные взвешивания.