Искусственная Нейронная Сеть — Hopfield Networks

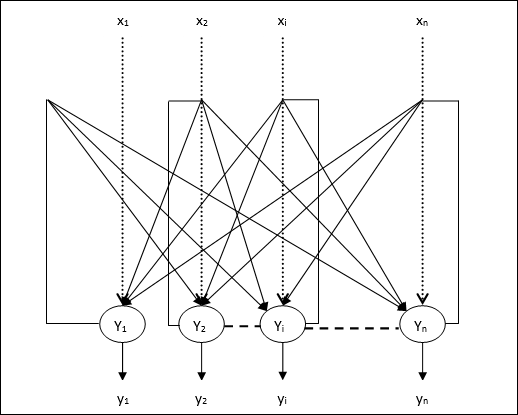
Нейронная сеть Хопфилда была изобретена доктором Джоном Дж. Хопфилдом в 1982 году. Она состоит из одного слоя, который содержит один или несколько полностью связанных рекуррентных нейронов. Сеть Хопфилда обычно используется для задач автоассоциирования и оптимизации.

Дискретная сеть Хопфилда

Сеть Хопфилда, которая работает в виде дискретных линий или, другими словами, можно сказать, что шаблоны ввода и вывода являются дискретными векторами, которые могут быть двоичными (0,1) или биполярными (+1, -1) по своей природе. Сеть имеет симметричные веса без самоподключений, т. _Е. W _ij = w _ji и w _ii = 0 .

Архитектура

Ниже приведены некоторые важные моменты, о которых следует помнить о дискретной сети Хопфилда.

• Эта модель состоит из нейронов с одним инвертирующим и одним неинвертирующим выходом.

• Выход каждого нейрона должен быть входом других нейронов, но не входом самого себя.

• Вес / прочность соединения обозначены как w _ij .

• Соединения могут быть как возбуждающими, так и тормозящими. Было бы возбуждающим, если выходной сигнал нейрона такой же, как входной, в противном случае тормозной.

• Веса должны быть симметричными, т.е. w _ij = w _ji

Эта модель состоит из нейронов с одним инвертирующим и одним неинвертирующим выходом.

Выход каждого нейрона должен быть входом других нейронов, но не входом самого себя.

Вес / прочность соединения обозначены как w _ij .

Соединения могут быть как возбуждающими, так и тормозящими. Было бы возбуждающим, если выходной сигнал нейрона такой же, как входной, в противном случае тормозной.

Веса должны быть симметричными, т.е. w _ij = w _ji

Выходные данные от Y _1, идущие к Y ₂ , Y _i и Y _n, имеют веса w ₁₂ , w _1i и w _1n соответственно. Точно так же другие дуги имеют веса на них.

Алгоритм обучения

Во время обучения дискретной сети Хопфилда веса будут обновляться. Поскольку мы знаем, что у нас могут быть двоичные входные векторы, а также биполярные входные векторы. Следовательно, в обоих случаях обновления веса могут быть выполнены со следующим соотношением

Случай 1 — Шаблоны двоичного ввода

Для набора бинарных паттернов s (p), p = 1 до P

Здесь s (p) = s ₁ (p), s ₂ (p), …, s _i (p), …, s _n (p)

Весовая матрица задается

wIJ= sumРр=1[2sя(р)−1][2sJ(р)−1]дляя NEQJ

$$w_ {IJ} \: = \: \ sum_ {р = 1} ^ Р [2s_ {я} (р) - \: 1] [2s_ {J} (р) - \: 1] \: \: \: \: \: для \: я \: \ NEQ \: J$$

Случай 2 — Биполярные модели ввода

Для набора бинарных паттернов s (p), p = 1 до P

Здесь s (p) = s ₁ (p), s ₂ (p), …, s _i (p), …, s _n (p)

Весовая матрица задается

wIJ= sumРр=1[Sя(р)][SJ(р)]для :я NEQJ

$$w_ {IJ} \: = \: \ sum_ {р = 1} ^ Р [S_ {я} (р)] [S_ {J} (р)] \: \: \: \: \: для \ : я \: \ NEQ \: J$$

Алгоритм тестирования

Шаг 1 — Инициализировать веса, которые получены из алгоритма обучения с использованием принципа Хебба.

Шаг 2 — Выполните шаги 3-9, если активации сети не консолидированы.

Шаг 3 — Для каждого входного вектора X выполните шаги 4-8.

Шаг 4 — Сделайте начальную активацию сети равной внешнему входному вектору X следующим образом —

у−я=Xядляя=1кп

$$у- {я} \: = \: X_ {я} \: \: \: для \: я \: = \: 1 \: к \: п$$

Шаг 5 — Для каждого блока Y _i выполните шаги 6-9.

Шаг 6 — Рассчитайте чистый вход сети следующим образом —

yини=xя + displaystyle сумма limitsjyJwджи

$$y_ {ини} \: = \: x_ {я} \ + \: \ displaystyle \ сумма \ limits_ {j} y_ {J} {w_ джи}$$

Шаг 7 — Примените активацию следующим образом к сетевому входу, чтобы рассчитать выходной сигнал —

y_ {i} \: = \ begin {case} 1 & if \: y_ {ini} \:> \: \ theta_ {i} \\ y_ {i} & if \: y_ {ini} \: = \: \ theta_ {i} \\ 0 & if \: y_ {ini} \: <\: \ theta_ {i} \ end {case}

$$y_ {i} \: = \ begin {case} 1 &amp;amp; if \: y_ {ini} \:&amp;gt; \: \ theta_ {i} \\ y_ {i} &amp;amp; if \: y_ {ini} \: = \: \ theta_ {i} \\ 0 &amp;amp; if \: y_ {ini} \: &amp;lt;\: \ theta_ {i} \ end {case}$$

Здесь  thetai$\ theta_ {i}$ — это порог.

Шаг 8 — Передайте этот вывод y _i всем другим устройствам.

Шаг 9 — Проверьте сеть на предмет соединения.

Оценка энергетической функции

Энергетическая функция определяется как функция, которая связана и не является возрастающей функцией состояния системы.

Энергетическая функция E _f ⁡, также называемая функцией Ляпунова, определяет устойчивость дискретной сети Хопфилда и характеризуется следующим образом:

Ef=− frac12 displaystyle sum limitni=1 displaystyle sum limitnj=1yiyjwij− displaystyle sum limitni=1xiyi+ displaystyle sum limitni=1 thetaiyi

$$E_ {f} \: = \: - \ frac {1} {2} \ displaystyle \ sum \ limit_ {i = 1} ^ n \ displaystyle \ sum \ limit_ {j = 1} ^ n y_ {i} y_ {j} w_ {ij} \: - \: \ displaystyle \ sum \ limit_ {i = 1} ^ n x_ {i} y_ {i} \: + \: \ displaystyle \ sum \ limit_ {i = 1} ^ n \ theta_ {i} y_ {i}$$

Условие — В стабильной сети, когда состояние узла изменяется, вышеуказанная энергетическая функция будет уменьшаться.

Предположим, что когда узел i изменил состояние с y(k)i$y_i ^ {(k)}$ на y(k+1)i$y_i ^ {(k \: + \: 1)}$, то изменение энергии  DeltaEf$\ Delta E_ {f}$ определяется выражением следующее отношение

 DeltaEf=Ef(y(k+1)i)−Ef(y(k)i)

$$\ Delta E_ {f} \: = \: E_ {f} (y_i ^ {(k + 1)}) \: - \: E_ {f} (y_i ^ {(k)})$$

=− left( beginarrayc displaystyle sum limitnj=1wijy(k)i+xi− thetaя конецмассива справа)(y(к+1)i−y(к)i)

$$= \: - \ left (\ begin {array} {c} \ displaystyle \ sum \ limit_ {j = 1} ^ n w_ {ij} y_i ^ {(k)} \: + \: x_ {i} \: - \: \ theta_ {я} \ {конец массива} \ справа) (y_i ^ {(к + 1)} \: - \: y_i ^ {(к)})$$

=− :(neti) Deltayi

$$= \: - \ 🙁 net_ {i}) \ Delta y_ {i}$$

Здесь  Deltayi=y(k+1)i−y(k)i$\ Delta y_ {i} \: = \: y_i ^ {(k \: + \: 1)} \: - \: y_i ^ {(k)}$

Изменение энергии зависит от того, что только одна единица может обновлять свою активацию одновременно.

Непрерывная сеть Хопфилда

По сравнению с дискретной сетью Хопфилда непрерывная сеть имеет время как непрерывную переменную. Он также используется в задачах автоассоциации и оптимизации, таких как задачи коммивояжера.

Модель — модель или архитектуру можно создать, добавив электрические компоненты, такие как усилители, которые могут сопоставить входное напряжение с выходным напряжением через функцию активации сигмоида.

Оценка энергетической функции

Ef= frac12 displaystyle sum limitni=1 sumn substackj=1j neiyiyjwij− displaystyle sum limitni=1xiyi+ frac1 lambda displaystyle sum limitni=1 sumn substackj=1j neiwijgri intyi0a−1(y)dy

$$E_f = \ frac {1} {2} \ displaystyle \ sum \ limit_ {i = 1} ^ n \ sum _ {\ substack {j = 1 \\ j \ ne i}} ^ n y_i y_j w_ {ij} - \ displaystyle \ sum \ limit_ {i = 1} ^ n x_i y_i + \ frac {1} {\ lambda} \ displaystyle \ sum \ limit_ {i = 1} ^ n \ sum _ {\ substack {j = 1 \\ j \ ne i}} ^ n w_ {ij} g_ {ri} \ int_ {0} ^ {y_i} a ^ {- 1} (y) dy$$

Здесь λ — параметр усиления и g _ri входная проводимость.