Другие методы оптимизации

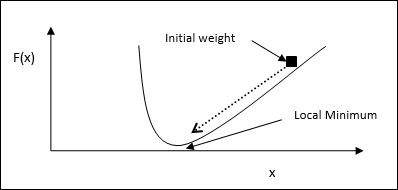
Градиентный спуск, также известный как самый крутой спуск, является алгоритмом итеративной оптимизации для нахождения локального минимума функции. Минимизируя функцию, мы заботимся о том, чтобы свести к минимуму затраты или ошибки (помните, что проблема с коммивояжером). Он широко используется в глубоком обучении, что полезно в самых разных ситуациях. Здесь следует помнить, что мы занимаемся локальной оптимизацией, а не глобальной оптимизацией.

Основная рабочая идея

Мы можем понять основную рабочую идею градиентного спуска с помощью следующих шагов —

• Сначала начните с первоначального предположения о решении.

• Затем возьмите градиент функции в этой точке.

• Позже, повторите процесс, шагая решение в отрицательном направлении градиента.

Сначала начните с первоначального предположения о решении.

Затем возьмите градиент функции в этой точке.

Позже, повторите процесс, шагая решение в отрицательном направлении градиента.

Следуя вышеуказанным шагам, алгоритм в конечном итоге сойдется там, где градиент равен нулю.

Математическая концепция

Предположим, у нас есть функция f (x), и мы пытаемся найти минимум этой функции. Ниже приведены шаги, чтобы найти минимум f (x) .

• Сначала укажите начальное значение x0forx$x_ {0} \: for \: x$

• Теперь возьмем функцию градиента $\ nabla f$ ⁡ of, с интуицией, что градиент даст наклон кривой в этом x, а ее направление будет указывать на увеличение функции, чтобы найти лучшее направление, чтобы минимизировать ее. ,

• Теперь измените х следующим образом —

  xn+1=xn− theta nablaf(xn) $$x_ {n \: + \: 1} \: = \: x_ {n} \: - \: \ theta \ nabla f (x_ {n})$$

Сначала укажите начальное значение x0forx$x_ {0} \: for \: x$

Теперь возьмем функцию градиента $\ nabla f$ ⁡ of, с интуицией, что градиент даст наклон кривой в этом x, а ее направление будет указывать на увеличение функции, чтобы найти лучшее направление, чтобы минимизировать ее. ,

Теперь измените х следующим образом —

xn+1=xn− theta nablaf(xn) $$x_ {n \: + \: 1} \: = \: x_ {n} \: - \: \ theta \ nabla f (x_ {n})$$

Здесь θ> 0 — скорость тренировки (размер шага), которая заставляет алгоритм делать небольшие прыжки.

Оценка размера шага

На самом деле неправильный размер шага θ может не достичь сходимости, поэтому очень важен тщательный отбор его. Следующие пункты должны быть запомнены при выборе размера шага

• Не выбирайте слишком большой размер шага, иначе он будет иметь негативное влияние, то есть он будет расходиться, а не сходиться.

• Не выбирайте слишком маленький размер шага, иначе это займет много времени, чтобы сходиться.

Не выбирайте слишком большой размер шага, иначе он будет иметь негативное влияние, то есть он будет расходиться, а не сходиться.

Не выбирайте слишком маленький размер шага, иначе это займет много времени, чтобы сходиться.

Некоторые варианты выбора размера шага —

• Один из вариантов — выбрать фиксированный размер шага.

• Другой вариант — выбрать другой размер шага для каждой итерации.

Один из вариантов — выбрать фиксированный размер шага.

Другой вариант — выбрать другой размер шага для каждой итерации.

Имитация отжига

Основная концепция имитации отжига (SA) мотивируется отжигом в твердых телах. В процессе отжига, если мы нагреем металл выше его температуры плавления и остудим, структурные свойства будут зависеть от скорости охлаждения. Можно также сказать, что SA имитирует металлургический процесс отжига.

Используйте в ANN

SA является стохастическим вычислительным методом, основанным на аналогии отжига, для аппроксимации глобальной оптимизации заданной функции. Мы можем использовать SA для обучения прямой связи нейронных сетей.

Алгоритм

Шаг 1 — Генерация случайного решения.

Шаг 2 — Рассчитайте его стоимость, используя некоторую функцию стоимости.

Шаг 3 — Генерация случайного соседнего решения.

Шаг 4 — Рассчитайте стоимость нового решения по той же функции стоимости.

Шаг 5 — Сравните стоимость нового решения со стоимостью старого решения следующим образом:

Если Cost _{New Solution} <Cost _{Old Solution,} перейдите к новому решению.

Шаг 6 — Проверьте условие остановки, которое может быть максимальным числом достигнутых итераций или получить приемлемое решение.