Природа всегда была источником вдохновения для всего человечества. Генетические алгоритмы (GA) — это алгоритмы поиска, основанные на понятиях естественного отбора и генетики. GA — это подмножество гораздо большей ветви вычислений, известной как эволюционные вычисления .
GA были разработаны Джоном Холландом и его студентами и коллегами из Мичиганского университета, прежде всего Дэвидом Э. Голдбергом, и с тех пор пробовали решать различные задачи оптимизации с высокой степенью успеха.
В ГА у нас есть пул или совокупность возможных решений данной проблемы. Эти решения затем подвергаются рекомбинации и мутации (как в естественной генетике), порождая новых детей, и процесс повторяется на протяжении разных поколений. Каждому индивидууму (или подходящему решению) присваивается значение пригодности (в зависимости от значения его целевой функции), и более подходящие индивидуумы получают более высокий шанс на спаривание и получают больше «более подходящих» индивидуумов. Это соответствует дарвиновской теории выживания наиболее приспособленных.
Таким образом, мы продолжаем «эволюционировать» лучших людей или решений из поколения в поколение, пока не достигнем критерия остановки.
Генетические алгоритмы по своей природе достаточно рандомизированы, однако они выполняют намного лучше, чем случайный локальный поиск (в котором мы просто пробуем различные случайные решения, отслеживая лучшие на данный момент), поскольку они также используют историческую информацию.
Преимущества ГА
У GA есть различные преимущества, которые сделали их чрезвычайно популярными. К ним относятся —
-
Не требует никакой производной информации (которая может быть недоступна для многих реальных проблем).
-
Это быстрее и эффективнее по сравнению с традиционными методами.
-
Имеет очень хорошие параллельные возможности.
-
Оптимизирует как непрерывные, так и дискретные функции, а также многоцелевые задачи.
-
Предоставляет список «хороших» решений, а не просто одно решение.
-
Всегда получает ответ на проблему, которая со временем становится лучше.
-
Полезно, когда пространство поиска очень велико и задействовано большое количество параметров.
Не требует никакой производной информации (которая может быть недоступна для многих реальных проблем).
Это быстрее и эффективнее по сравнению с традиционными методами.
Имеет очень хорошие параллельные возможности.
Оптимизирует как непрерывные, так и дискретные функции, а также многоцелевые задачи.
Предоставляет список «хороших» решений, а не просто одно решение.
Всегда получает ответ на проблему, которая со временем становится лучше.
Полезно, когда пространство поиска очень велико и задействовано большое количество параметров.
Ограничения ГА
Как и любая техника, GA также страдает от нескольких ограничений. К ним относятся —
-
GA не подходят для всех проблем, особенно для задач, которые просты и для которых доступна производная информация.
-
Значение пригодности рассчитывается многократно, что может быть вычислительно дорогостоящим для некоторых задач.
-
Будучи стохастическим, нет никаких гарантий относительно оптимальности или качества решения.
-
Если не реализовано должным образом, GA может не сходиться к оптимальному решению.
GA не подходят для всех проблем, особенно для задач, которые просты и для которых доступна производная информация.
Значение пригодности рассчитывается многократно, что может быть вычислительно дорогостоящим для некоторых задач.
Будучи стохастическим, нет никаких гарантий относительно оптимальности или качества решения.
Если не реализовано должным образом, GA может не сходиться к оптимальному решению.
GA — Мотивация
Генетические алгоритмы обладают способностью предоставлять «достаточно хорошее» решение «достаточно быстро». Это делает газ привлекательным для использования при решении задач оптимизации. Причины, по которым нужны ГА, следующие:
Решение сложных проблем
В информатике существует большой набор проблем, которые NP-Hard . По сути это означает, что даже самым мощным вычислительным системам требуется очень много времени (даже лет!) Для решения этой проблемы. В таком сценарии ГА оказываются эффективным инструментом для предоставления практически оптимальных решений за короткое время.
Отказ градиентных методов
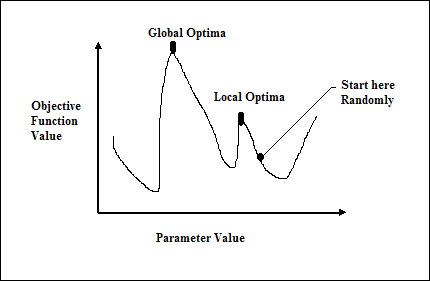
Традиционные методы, основанные на исчислении, работают, начиная со случайной точки и двигаясь в направлении градиента, пока мы не достигнем вершины холма. Этот метод эффективен и очень хорошо работает для однопиковых целевых функций, таких как функция стоимости в линейной регрессии. Однако в большинстве реальных ситуаций у нас есть очень сложная проблема, называемая ландшафтами, состоящими из множества пиков и многих долин, что приводит к сбою таких методов, поскольку они страдают от присущей им тенденции застрять в локальных оптимумах, как показано на следующем рисунке.
Быстрое получение хорошего решения
У некоторых сложных проблем, таких как Задача коммивояжера (TSP), есть реальные приложения, такие как поиск пути и VLSI Design. Теперь представьте, что вы используете свою систему GPS-навигации, и для расчета «оптимального» пути от источника до пункта назначения требуется несколько минут (или даже нескольких часов). Задержка в таких реальных приложениях неприемлема, и поэтому требуется «достаточно хорошее» решение, которое доставляется «быстро».
Как использовать GA для задач оптимизации?
Мы уже знаем, что оптимизация — это действие, направленное на то, чтобы сделать что-то вроде дизайна, ситуации, ресурса и системы как можно более эффективным. Процесс оптимизации показан на следующей диаграмме.
Этапы механизма GA для процесса оптимизации
Далее приведены этапы механизма ГА при использовании для оптимизации задач.
Генерация начальной популяции случайным образом.
Выберите исходное решение с наилучшими значениями пригодности.
Рекомбинируйте выбранные решения, используя операторы мутации и кроссовера.
Вставьте потомство в популяцию.
Теперь, если условие остановки выполнено, верните решение с наилучшим значением пригодности. В противном случае перейдите к шагу 2.