Изучение вектора квантования

Векторное квантование обучения (LVQ), отличающееся от векторного квантования (VQ) и самоорганизующихся карт Кохонена (KSOM), в основном представляет собой конкурентную сеть, в которой используется контролируемое обучение. Мы можем определить его как процесс классификации шаблонов, где каждая единица вывода представляет класс. Поскольку он использует контролируемое обучение, сети будет предоставлен набор обучающих шаблонов с известной классификацией наряду с начальным распределением выходного класса. После завершения процесса обучения LVQ классифицирует входной вектор, назначая его тому же классу, что и выходной блок.

Архитектура

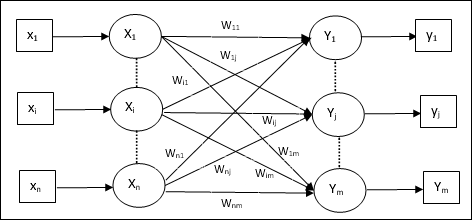
На следующем рисунке показана архитектура LVQ, которая очень похожа на архитектуру KSOM. Как мы видим, существует «n» количество единиц ввода и «m» количество единиц вывода. Слои полностью взаимосвязаны с весом на них.

Используемые параметры

Ниже приведены параметры, используемые в процессе обучения LVQ, а также в блок-схеме

• x = вектор обучения (x ₁ , …, x _i , …, x _n )

• T = класс для обучающего вектора x

• w _j = весовой вектор для j- ^й единицы измерения

• C _j = класс, связанный с j- ^й единицей вывода

x = вектор обучения (x ₁ , …, x _i , …, x _n )

T = класс для обучающего вектора x

w _j = весовой вектор для j- ^й единицы измерения

C _j = класс, связанный с j- ^й единицей вывода

Алгоритм обучения

Шаг 1 — Инициализировать опорные векторы, что можно сделать следующим образом:

• Шаг 1 (а) — Из данного набора тренировочных векторов взять первые « m » (количество кластеров) тренировочных векторов и использовать их в качестве весовых векторов. Остальные векторы могут быть использованы для обучения.

• Шаг 1 (б) — Присвойте начальный вес и классификацию случайным образом.

• Шаг 1 (с) — Применение метода кластеризации K-средних.

Шаг 1 (а) — Из данного набора тренировочных векторов взять первые « m » (количество кластеров) тренировочных векторов и использовать их в качестве весовых векторов. Остальные векторы могут быть использованы для обучения.

Шаг 1 (б) — Присвойте начальный вес и классификацию случайным образом.

Шаг 1 (с) — Применение метода кластеризации K-средних.

Шаг 2 — Инициализировать опорный вектор $\ alpha$

Шаг 3 — Продолжайте с шагов 4-9, если условие остановки этого алгоритма не выполняется.

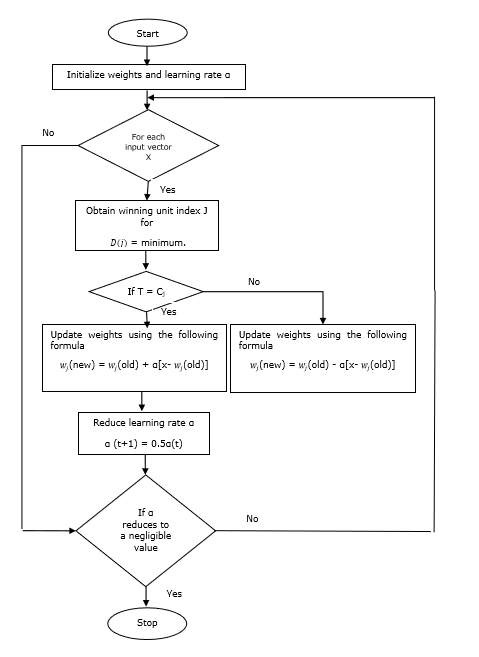
Шаг 4 — Выполните шаги 5-6 для каждого входного вектора обучения x .

Шаг 5 — Рассчитать квадрат евклидова расстояния для j = 1 до m и i = от 1 до n

D(j)= displaystyle sum limitni=1 displaystyle sum limitmj=1(xi−wij)2 $$D (j) \: = \: \ displaystyle \ sum \ limit_ {i = 1} ^ n \ displaystyle \ sum \ limit_ {j = 1} ^ m (x_ {i} \: - \: w_ {ij }) ^ 2$$

Шаг 6 — Получить выигрышную единицу J, где D (j) минимально.

Шаг 7 — Рассчитайте новый вес выигрышной единицы по следующему соотношению —

если T = C _j, то wj(новый)=wj(старый)+ alpha[x−wj(старый)]$w_ {j} (новый) \: = \: w_ {j} (старый) \: + \: \ alpha [x \: - \: w_ {j} (старый)]$

если T ≠ C _j, то wj(новый)=wj(старый)− alpha[x−wj(старый)]$w_ {j} (новый) \: = \: w_ {j} (старый) \: - \: \ alpha [x \: - \: w_ {j} (старый)]$

Шаг 8 — Уменьшите скорость обучения $\ alpha$.

Шаг 9 — Проверка состояния остановки. Это может быть следующим:

• Максимальное количество эпох достигнуто.
• Скорость обучения снижена до незначительного значения.

блок-схема

Варианты

Три других варианта, а именно LVQ2, LVQ2.1 и LVQ3, были разработаны Кохоненом. Сложность во всех этих трех вариантах из-за концепции, которую изучат победитель и юнит, занявший второе место, больше, чем в LVQ.

LVQ2

Как уже обсуждалось, концепция других вариантов LVQ выше, состояние LVQ2 формируется окном. Это окно будет основано на следующих параметрах —

• х — текущий входной вектор

• y _c — опорный вектор, ближайший к x

• y _r — другой опорный вектор, ближайший к x

• d _c — расстояние от x до y _c

• d _r — расстояние от x до y _r

х — текущий входной вектор

y _c — опорный вектор, ближайший к x

y _r — другой опорный вектор, ближайший к x

d _c — расстояние от x до y _c

d _r — расстояние от x до y _r

Входной вектор х попадает в окно, если

 гидроразрываDCDг>1− тетаи гидроразрываDгDс>1 + Theta $$\ гидроразрыва {D_ {C}} {D_ {г}} \:> \: 1 \: - \: \ тета \: \: и \: \: \ гидроразрыва {D_ {г}} {D_ {с }} \:> \: 1 \ + \: \ Theta$$

Здесь $\ theta$ — количество обучающих образцов.

Обновление можно выполнить по следующей формуле:

У−с(т +1)=у−C(т) + альфа(т)[х(т)−у−C(t)]$У- {с} (т \ + \: 1) \: = \: у- {C} (т) \ + \: \ альфа (т) [х (т) \: - \: у- {C} (t)]$ (принадлежит к другому классу)

У−г(т +1)=у−г(т) + альфа(т)[х(т)−у−г(t)]$У- {г} (т \ + \: 1) \: = \: у- {г} (т) \ + \: \ альфа (т) [х (т) \: - \: у- {г} (t)]$ (принадлежит к тому же классу)

Здесь $\ alpha$ — скорость обучения.

LVQ2.1

В LVQ2.1 мы возьмем два ближайших вектора, а именно y _c1 и y _c2, и условие для окна следующее:

Min начинаютсяbmatrix гидроразрываDc1Dc2, гидроразрываDc2Dc1 конецbmatrix> :(1 :− Theta) $$Min \ {начинаются bmatrix} \ гидроразрыва {D_ {c1}} {D_ {c2}}, \ гидроразрыва {D_ {c2}} {D_ {c1}} \ {конец bmatrix} \:> \ 🙁 1 \ : - \: \ Theta)$$

Max начинаютсяbmatrix гидроразрываDc1Dc2, гидроразрываDc2Dc1 конецbmatrix < :(1 :+ тета) $$Max \ {начинаются bmatrix} \ гидроразрыва {D_ {c1}} {D_ {c2}}, \ гидроразрыва {D_ {c2}} {D_ {c1}} \ {конец bmatrix} \ &amp;lt;\ 🙁 1 \ : + \: \ тета)$$

Обновление можно выполнить по следующей формуле:

У−c1(т +1)=у−c1(т) + альфа(т)[х(т)−у−c1(t)]$У- {c1} (т \ + \: 1) \: = \: у- {c1} (т) \ + \: \ альфа (т) [х (т) \: - \: у- {c1} (t)]$ (принадлежит к другому классу)

У−с2(т +1)=у−с2(т) + альфа(т)[х(т)−у−с2(t)]$У- {с2} (т \ + \: 1) \: = \: у- {с2} (т) \ + \: \ альфа (т) [х (т) \: - \: у- {с2} (t)]$ (принадлежит к тому же классу)

Здесь $\ alpha$ — это скорость обучения.

LVQ3

В LVQ3 мы возьмем два ближайших вектора, а именно y _c1 и y _c2, и условие для окна будет следующим:

Min начинаютсяbmatrix гидроразрываDc1Dc2, гидроразрываDc2Dc1 конецbmatrix> :(1 :− тета)(1 + тета) $$Min \ {начинаются bmatrix} \ гидроразрыва {D_ {c1}} {D_ {c2}}, \ гидроразрыва {D_ {c2}} {D_ {c1}} \ {конец bmatrix} \:&amp;gt; \ 🙁 1 \ : - \: \ тета) (1 \ + \: \ тета)$$

Здесь $\ theta \ ок. 0,2$

Обновление можно выполнить по следующей формуле:

У−c1(т +1)=у−c1(т) + бета(т)[х(т)−у−c1(t)]$У- {c1} (т \ + \: 1) \: = \: у- {c1} (т) \ + \: \ бета (т) [х (т) \: - \: у- {c1} (t)]$ (принадлежит к другому классу)

У−с2(т +1)=у−с2(т) + бета(т)[х(т)−у−с2(t)]$У- {с2} (т \ + \: 1) \: = \: у- {с2} (т) \ + \: \ бета (т) [х (т) \: - \: у- {с2} (t)]$ (принадлежит к тому же классу)

Здесь $\ beta$ — это кратное значение скорости обучения $\ alpha$ и  beta=m alpha(t)$\ beta \: = \: m \ alpha (t)$ для каждых 0,1 <m <0,5