Обучение и адаптация

Как указывалось ранее, ANN полностью вдохновлен тем, как работает биологическая нервная система, т.е. мозг человека. Самая впечатляющая характеристика человеческого мозга — учиться, поэтому ANN приобретает такую ​​же особенность.

Что такое обучение в ANN?

По сути, обучение означает делать и адаптировать изменения в себе по мере изменения среды. ИНС — это сложная система, или, точнее, мы можем сказать, что это сложная адаптивная система, которая может изменять свою внутреннюю структуру на основе информации, проходящей через нее.

Почему это важно?

Будучи сложной адаптивной системой, обучение в ANN подразумевает, что блок обработки способен изменять свое поведение ввода / вывода из-за изменения среды. Важность обучения в ИНС возрастает из-за фиксированной функции активации, а также вектора ввода / вывода, когда создается конкретная сеть. Теперь, чтобы изменить поведение ввода / вывода, нам нужно отрегулировать веса.

классификация

Это может быть определено как процесс обучения различению данных образцов на разные классы путем нахождения общих черт между образцами одного и того же класса. Например, для обучения ANN у нас есть несколько обучающих образцов с уникальными функциями, а для его тестирования у нас есть несколько тестовых образцов с другими уникальными функциями. Классификация является примером контролируемого обучения.

Правила обучения нейронной сети

Мы знаем, что во время обучения ANN, чтобы изменить поведение ввода / вывода, нам нужно отрегулировать веса. Следовательно, требуется метод, с помощью которого веса могут быть изменены. Эти методы называются правилами обучения, которые являются просто алгоритмами или уравнениями. Ниже приведены некоторые правила обучения для нейронной сети.

Правило изучения иврита

Это правило, одно из старейших и самых простых, было введено Дональдом Хеббом в его книге «Организация поведения» в 1949 году. Это своего рода прямое, неконтролируемое обучение.

Основная концепция — это правило основано на предложении Хебба, который написал:

«Когда аксон клетки A находится достаточно близко, чтобы возбудить клетку B, и многократно или постоянно принимает участие в ее сжигании, в одной или обеих клетках происходит некоторый процесс роста или метаболические изменения, так что A эффективно, как одна из клеток, запускающих B , увеличена.»

Из приведенного выше постулата мы можем сделать вывод, что связи между двумя нейронами могут быть усилены, если нейроны срабатывают одновременно, и могут ослабнуть, если они срабатывают в разное время.

Математическая формулировка. Согласно правилу обучения Хевбия, следующая формула увеличивает вес соединения на каждом временном шаге.

 Deltawji(t)= alphaxi(t).yj(t) $$\ Delta w_ {ji} (t) \: = \: \ alpha x_ {i} (t) .y_ {j} (t)$$

Здесь $\ Delta w_ {ji} (t)$ ⁡ = приращение, на которое увеличивается вес соединения на шаге времени t

$\ alpha$ = положительная и постоянная скорость обучения

$x_ {i} (t)$ = входное значение пресинаптического нейрона на временном шаге t

$y_ {i} (t)$ = выход пресинаптического нейрона на шаге времени t

Правило обучения Перцептрона

Это правило является ошибкой исправления контролируемого алгоритма обучения однослойных сетей с прямой связью с линейной функцией активации, представленного Розенблаттом.

Базовая концепция. Будучи контролируемой по своей природе, для расчета ошибки будет проводиться сравнение между желаемым / целевым выходом и фактическим выходом. Если обнаруживается какая-либо разница, необходимо изменить вес соединения.

Математическая формулировка. Чтобы объяснить математическую формулировку, предположим, что у нас есть «n» число конечных входных векторов, x (n), вместе с его желаемым / целевым выходным вектором t (n), где от n = 1 до N.

Теперь выходной сигнал ‘y’ может быть рассчитан, как объяснено ранее, на основе чистого ввода, а функция активации, применяемая к этому сетевому вводу, может быть выражена следующим образом:

$$y \: = \: f (y_ {in}) \: = \: \ begin {case} 1, & y_ {in} \:> \: \ theta \\ 0, & y_ {in} \: \ leqslant \: \ Theta \ конец {случаи}$$

Где θ — порог.

Обновление веса может быть сделано в следующих двух случаях —

Случай I — когда ты , то

ш(новый)=W(старый) +ТХ $$ш (новый) \: = \: W (старый) \ + \; ТХ$$

Случай II — когда t = y , то

Без изменений в весе

Delta Learning Rule (правило Уидроу-Хоффа)

Он введен Бернардом Уидроу и Марсианом Хоффом, также называемым методом наименьшего среднего квадрата (LMS), чтобы минимизировать ошибку во всех шаблонах обучения. Это своего рода контролируемый алгоритм обучения с функцией непрерывной активации.

Основная концепция . Основой этого правила является подход с градиентным спуском, который продолжается вечно. Дельта-правило обновляет синаптические веса, чтобы минимизировать чистый входной сигнал для выходной единицы и целевого значения.

Математическая формулировка — Чтобы обновить синаптические веса, дельта-правило задается

 Deltawi= alpha :.xi.ej $$\ Delta w_ {i} \: = \: \ alpha \ :. x_ {i} .e_ {j}$$

Здесь $\ Delta w_ {i}$ = изменение веса для i- ^го шаблона;

$\ alpha$ = положительная и постоянная скорость обучения;

$x_ {i}$ = входное значение от пресинаптического нейрона;

$e_ {j}$ = (t−yin)$(t \: - \: y_ {in})$, разница между желаемым / целевым выходом и фактическим выходом y $y_ {in}$

Вышеуказанное дельта-правило относится только к одному выходному устройству.

Обновление веса может быть сделано в следующих двух случаях —

Случай I — когда ты , то

w(новый)=w(старый)+ Deltaw $$w (новый) \: = \: w (старый) \: + \: \ Delta w$$

Случай II — когда t = y , то

Без изменений в весе

Конкурентное правило обучения (победитель получает все)

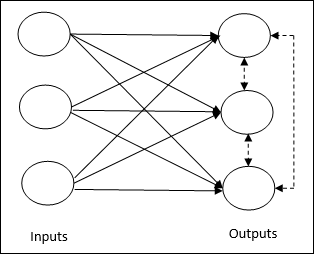
Он связан с обучением без присмотра, при котором выходные узлы пытаются конкурировать друг с другом, чтобы представить шаблон ввода. Чтобы понять это правило обучения, мы должны понимать конкурентную сеть, которая представлена ​​следующим образом:

Основная концепция конкурентной сети. Эта сеть похожа на однослойную сеть с прямой связью с обратной связью между выходами. Соединения между выходами имеют запретительный тип, показанный пунктирными линиями, что означает, что конкуренты никогда не поддерживают себя.

Основная концепция правила конкурентного обучения. Как было сказано ранее, между узлами вывода будет конкуренция. Следовательно, основная концепция заключается в том, что во время обучения выходной блок с наивысшей активацией для данного шаблона ввода будет объявлен победителем. Это правило также называется Победитель получает все, потому что обновляется только выигрышный нейрон, а остальные нейроны остаются без изменений.

Математическая формулировка — Ниже приведены три важных фактора для математической формулировки этого правила обучения —

• Условие быть победителем — Предположим, что если нейрон $y_ {k}$ ⁡ ⁡ хочет быть победителем, то будет выполнено следующее условие:

  $$y_ {k} \: = \: \ begin {case} 1 & if \: v_ {k} \:> \: v_ {j} \: для \: все \: j, \: j \: \ neq \: k \\ 0 & в противном случае \ end {case}$$

Условие быть победителем — Предположим, что если нейрон $y_ {k}$ ⁡ ⁡ хочет быть победителем, то будет выполнено следующее условие:

$$y_ {k} \: = \: \ begin {case} 1 & if \: v_ {k} \:> \: v_ {j} \: для \: все \: j, \: j \: \ neq \: k \\ 0 & в противном случае \ end {case}$$

Это означает, что если какой-либо нейрон, скажем, $y_ {k}$ wants, хочет победить, то его индуцированное локальное поле (вывод единицы суммирования), скажем, $v_ {k}$, должно быть наибольшим среди всех других нейронов. в сети.

• Условие суммирования общего веса. Другое ограничение по правилу конкурентного обучения состоит в том, что сумма весов для конкретного выходного нейрона будет равна 1. Например, если мы рассмотрим нейрон k, то —

   displaystyle сумма limitsJwкдж=1длявсеK $$\ displaystyle \ сумма \ limits_ {J} {w_ кдж} \: = \: 1 \: \: \: \: \: \: \: \: \: для \: все \: K$$

Условие суммирования общего веса. Другое ограничение по правилу конкурентного обучения состоит в том, что сумма весов для конкретного выходного нейрона будет равна 1. Например, если мы рассмотрим нейрон k, то —

 displaystyle сумма limitsJwкдж=1длявсеK $$\ displaystyle \ сумма \ limits_ {J} {w_ кдж} \: = \: 1 \: \: \: \: \: \: \: \: \: для \: все \: K$$

• Изменение веса для победителя — если нейрон не реагирует на шаблон ввода, то обучение в этом нейроне не происходит. Однако, если конкретный нейрон выигрывает, то соответствующие веса корректируются следующим образом

  $$\ Delta w_ {kj} \: = \: \ begin {case} - \ alpha (x_ {j} \: - \: w_ {kj}), & if \: нейрон \: k \: wins \\ 0, и если \: нейрон \: k \: убытки \ конец {случаи}$$

Изменение веса для победителя — если нейрон не реагирует на шаблон ввода, то обучение в этом нейроне не происходит. Однако, если конкретный нейрон выигрывает, то соответствующие веса корректируются следующим образом

$$\ Delta w_ {kj} \: = \: \ begin {case} - \ alpha (x_ {j} \: - \: w_ {kj}), & if \: нейрон \: k \: wins \\ 0, и если \: нейрон \: k \: убытки \ конец {случаи}$$

Здесь $\ alpha$ — скорость обучения.

Это ясно показывает, что мы отдаем предпочтение выигрышному нейрону, регулируя его вес, и если происходит потеря нейрона, нам не нужно беспокоиться о том, чтобы заново отрегулировать его вес.

Внешнее Правило Обучения

Это правило, введенное Гроссбергом, касается контролируемого обучения, потому что желаемые результаты известны. Это также называется обучением Гроссберга.

Основная концепция — это правило применяется к нейронам, расположенным в слое. Он специально разработан для получения желаемого выхода d слоя p нейронов.

Математическая формулировка — поправки веса в этом правиле рассчитываются следующим образом

 Deltawj= alpha :(d−wj) $$\ Delta w_ {j} \: = \: \ alpha \ 🙁 d \: - \: w_ {j})$$

Здесь d — желаемый выход нейрона, а $\ alpha$ — скорость обучения.