Машина Больцмана

Это стохастические процессы обучения, имеющие рекуррентную структуру и являются основой ранних методов оптимизации, используемых в ANN. Машина Больцмана была изобретена Джеффри Хинтоном и Терри Сейновски в 1985 году. Больше ясности можно наблюдать в словах Хинтона о Машине Больцмана.

«Удивительной особенностью этой сети является то, что она использует только локально доступную информацию. Изменение веса зависит только от поведения двух соединяемых им блоков, даже если изменение оптимизирует глобальную меру »- Ackley, Hinton 1985.

Несколько важных моментов о машине Больцмана —

• Они используют рекуррентную структуру.

• Они состоят из стохастических нейронов, которые имеют одно из двух возможных состояний: 1 или 0.

• Некоторые из нейронов в этом являются адаптивными (свободное состояние), а некоторые зажаты (замороженное состояние).

• Если применить дискретный отжиг к дискретной сети Хопфилда, то она станет машиной Больцмана.

Они используют рекуррентную структуру.

Они состоят из стохастических нейронов, которые имеют одно из двух возможных состояний: 1 или 0.

Некоторые из нейронов в этом являются адаптивными (свободное состояние), а некоторые зажаты (замороженное состояние).

Если применить дискретный отжиг к дискретной сети Хопфилда, то она станет машиной Больцмана.

Цель машины Больцмана

Основная цель Boltzmann Machine — оптимизировать решение проблемы. Задачей Boltzmann Machine является оптимизация веса и количества, связанных с этой конкретной проблемой.

Архитектура

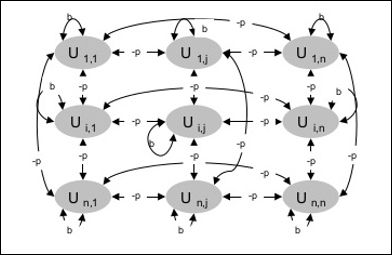
Следующая диаграмма показывает архитектуру машины Больцмана. Из диаграммы видно, что это двумерный массив единиц. Здесь веса на соединениях между единицами равны –p, где p> 0 . Веса самоподключений определяются как b, где b> 0 .

Алгоритм обучения

Поскольку мы знаем, что машины Больцмана имеют фиксированные веса, следовательно, не будет никакого обучающего алгоритма, поскольку нам не нужно обновлять веса в сети. Однако, чтобы проверить сеть, мы должны установить веса, а также найти консенсус-функцию (CF).

Машина Больцмана имеет набор узлов U _i и U _j и имеет двунаправленные соединения на них.

• Мы рассматриваем фиксированный вес, скажем, w _ij .

• w _ij ≠ 0, если U _i и U _j связаны.

• Также существует симметрия во взвешенном соединении, то есть w _ij = w _ji .

• w _ii также существует, то есть будет самостоятельная связь между единицами.

• Для любого блока U _i его состояние u _i будет равно 1 или 0.

Мы рассматриваем фиксированный вес, скажем, w _ij .

w _ij ≠ 0, если U _i и U _j связаны.

Также существует симметрия во взвешенном соединении, то есть w _ij = w _ji .

w _ii также существует, то есть будет самостоятельная связь между единицами.

Для любого блока U _i его состояние u _i будет равно 1 или 0.

Основная цель машины Больцмана — максимизировать функцию согласия (CF), которая может быть задана следующим соотношением

$$ CF \: = \: \ displaystyle \ sum \ limit_ {i} \ displaystyle \ sum \ limit_ {j \ leqslant i} w_ {ij} u_ {i} u_ {j} $$

Теперь, когда состояние изменяется от 1 до 0 или от 0 до 1, тогда изменение в консенсусе может быть задано следующим соотношением:

$$ \ Delta CF \: = \ 🙁 1 \: — \: 2u_ {i}) (w_ {ij} \: + \: \ displaystyle \ sum \ limit_ {j \ neq i} u_ {i} w_ { IJ}) $$

Здесь u _i — текущее состояние U _i .

Изменение коэффициента ( 1 — 2u _i ) определяется следующим соотношением:

$$ (1 \: — \: 2u_ {i}) \: = \: \ begin {case} +1, & U_ {i} \: is \: в настоящее время \: выключен \\ — 1, & U_ {i } \: есть \: в настоящее время \: \ на конце {случаи} $$

Обычно единица U _i не меняет своего состояния, но если это так, то информация будет находиться локально для единицы. С этим изменением также будет достигнут консенсус в сети.

Вероятность того, что сеть примет изменение состояния устройства, определяется следующим соотношением:

$$ AF (i, T) \: = \: \ frac {1} {1 \: + \: exp [- \ frac {\ Delta CF (i)} {T}]} $$

Здесь T является управляющим параметром. Он будет уменьшаться, когда CF достигает максимального значения.

Алгоритм тестирования

Шаг 1 — Инициализируйте следующее, чтобы начать тренировку —

• Веса, представляющие ограничение задачи
• Контрольный параметр T

Шаг 2 — Продолжайте шаги 3-8, когда условие остановки не соответствует действительности.

Шаг 3 — Выполните шаги 4-7.

Шаг 4 — Предположим, что одно из состояний изменило вес, и выберите целое число I, J в качестве случайных значений от 1 до n .

Шаг 5 — Рассчитайте изменение консенсуса следующим образом —

$$ \ Delta CF \: = \ 🙁 1 \: — \: 2u_ {i}) (w_ {ij} \: + \: \ displaystyle \ sum \ limit_ {j \ neq i} u_ {i} w_ { IJ}) $$

Шаг 6 — Рассчитайте вероятность того, что эта сеть примет изменение состояния

$$ AF (i, T) \: = \: \ frac {1} {1 \: + \: exp [- \ frac {\ Delta CF (i)} {T}]} $$

Шаг 7 — Принять или отклонить это изменение следующим образом —

Случай I — если R <AF , принять изменение.

Случай II — если R ≥ AF , отклонить изменение.

Здесь R — случайное число от 0 до 1.

Шаг 8 — Уменьшите контрольный параметр (температуру) следующим образом —

T (новый) = .90,95T (старый)

Шаг 9 — Проверка условий остановки, которые могут быть следующими: