Обучение без учителя

Как следует из названия, этот тип обучения осуществляется без присмотра учителя. Этот процесс обучения является независимым. Во время обучения ANN при обучении без учителя входные векторы аналогичного типа объединяются в кластеры. Когда применяется новый шаблон ввода, то нейронная сеть выдает ответ с указанием класса, которому принадлежит шаблон ввода. При этом не будет обратной связи от среды относительно того, каким должен быть желаемый результат и является ли он правильным или неправильным. Следовательно, в этом типе обучения сама сеть должна обнаруживать шаблоны, особенности из входных данных и отношение для входных данных по выходу.

Winner-Takes-All Networks

Эти виды сетей основаны на правиле конкурентного обучения и будут использовать стратегию, при которой нейрон выбирается с наибольшим суммарным вкладом в качестве победителя. Соединения между выходными нейронами показывают конкуренцию между ними, и один из них будет «ВКЛ», что означает, что он будет победителем, а другие «ВЫКЛ».

Ниже приведены некоторые сети, основанные на этой простой концепции, использующей обучение без учителя.

Сеть Хемминга

В большинстве нейронных сетей, использующих неконтролируемое обучение, важно вычислить расстояние и выполнить сравнение. Этот вид сети представляет собой сеть Хемминга, где для каждого заданного входного вектора она будет сгруппирована в разные группы. Ниже приведены некоторые важные особенности сетей Хемминга.

• Липпманн начал работать над сетями Хэмминга в 1987 году.

• Это однослойная сеть.

• Входные данные могут быть двоичными {0, 1} из биполярных {-1, 1}.

• Веса сети рассчитываются по примерным векторам.

• Это сеть с фиксированным весом, что означает, что веса останутся неизменными даже во время тренировок.

Липпманн начал работать над сетями Хэмминга в 1987 году.

Это однослойная сеть.

Входные данные могут быть двоичными {0, 1} из биполярных {-1, 1}.

Веса сети рассчитываются по примерным векторам.

Это сеть с фиксированным весом, что означает, что веса останутся неизменными даже во время тренировок.

Макс Чистый

Это также сеть с фиксированным весом, которая служит подсетью для выбора узла, имеющего самый высокий вход. Все узлы полностью взаимосвязаны, и во всех этих взвешенных взаимосвязях существуют симметричные веса.

Архитектура

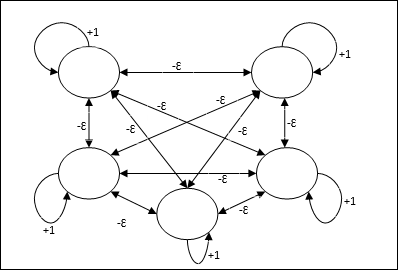
Он использует механизм, который является итеративным процессом, и каждый узел получает запрещающие входные данные от всех других узлов через соединения. Один узел, значение которого является максимальным, будет активным или победителем, а активации всех других узлов будут неактивными. Max Net использует функцию активации личности с $$f (x) \: = \: \ begin {case} x & if \: x> 0 \\ 0 & if \: x \ leq 0 \ end {case}$$

Задача этой сети достигается за счет веса самовозбуждения +1 и величины взаимного торможения, которая устанавливается как [0 <ɛ <$\ frac {1} {m}$], где «m» — это общее число узлы.

Конкурентное обучение в ANN

Он связан с обучением без присмотра, при котором выходные узлы пытаются конкурировать друг с другом, чтобы представить шаблон ввода. Чтобы понять это правило обучения, нам нужно понять конкурентную сеть, которая объясняется следующим образом:

Основная концепция конкурентной сети

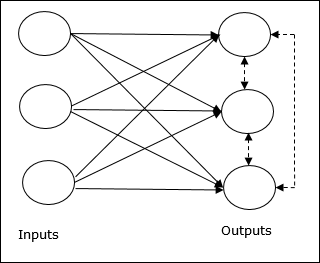
Эта сеть подобна однослойной сети прямой связи, имеющей соединение обратной связи между выходами. Соединения между выходами имеют запретительный тип, что показано пунктирными линиями, что означает, что конкуренты никогда не поддерживают себя.

Основная концепция правила конкурентного обучения

Как было сказано ранее, между узлами вывода будет конкуренция, поэтому основная концепция заключается в том, что во время обучения модуль вывода, который имеет наибольшую активацию для данного шаблона ввода, будет объявлен победителем. Это правило также называется Победитель получает все, потому что обновляется только выигрышный нейрон, а остальные нейроны остаются без изменений.

Математическая формулировка

Ниже приведены три важных фактора для математической формулировки этого правила обучения:

• Условие быть победителем

  Предположим, что если нейрон y _k хочет быть победителем, тогда будет следующее условие

  $$y_ {k} \: = \: \ begin {case} 1 &amp;amp; if \: v_ {k}&amp;gt; v_ {j} \: for \: all \: \: j, \: j \: \ neq \ : k \\ 0 &amp;amp; в противном случае \ end {case}$$

  Это означает, что если какой-либо нейрон, скажем, y _k хочет победить, то его индуцированное локальное поле (выходной сигнал единицы суммирования), скажем, v _k , должно быть наибольшим среди всех других нейронов в сети.

• Условие суммы суммы веса

  Другим ограничением для правила конкурентного обучения является общая сумма весов для конкретного выходного нейрона, равная 1. Например, если мы рассмотрим нейрон k, то

   displaystyle sum limitkwkj=1forвсеk $$\ displaystyle \ sum \ limit_ {k} w_ {kj} \: = \: 1 \: \: \: \: for \: все \: \: k$$

• Смена веса для победителя

  Если нейрон не реагирует на шаблон ввода, то обучение в этом нейроне не происходит. Однако, если конкретный нейрон выигрывает, то соответствующие веса корректируются следующим образом:

  $$\ Delta w_ {kj} \: = \: \ begin {case} - \ alpha (x_ {j} \: - \: w_ {kj}), &amp;amp; if \: нейрон \: k \: wins \\ 0 &amp;amp; if \: нейрон \: k \: убытки \ конец {случаи}$$

  Здесь $\ alpha$ — скорость обучения.

  Это ясно показывает, что мы отдаем предпочтение выигрышному нейрону, регулируя его вес, и, если нейрон потерян, нам не нужно беспокоиться о том, чтобы перенастроить его вес.

Условие быть победителем

Предположим, что если нейрон y _k хочет быть победителем, тогда будет следующее условие

$$y_ {k} \: = \: \ begin {case} 1 &amp;amp; if \: v_ {k}&amp;gt; v_ {j} \: for \: all \: \: j, \: j \: \ neq \ : k \\ 0 &amp;amp; в противном случае \ end {case}$$

Это означает, что если какой-либо нейрон, скажем, y _k хочет победить, то его индуцированное локальное поле (выходной сигнал единицы суммирования), скажем, v _k , должно быть наибольшим среди всех других нейронов в сети.

Условие суммы суммы веса

Другим ограничением для правила конкурентного обучения является общая сумма весов для конкретного выходного нейрона, равная 1. Например, если мы рассмотрим нейрон k, то

 displaystyle sum limitkwkj=1forвсеk $$\ displaystyle \ sum \ limit_ {k} w_ {kj} \: = \: 1 \: \: \: \: for \: все \: \: k$$

Смена веса для победителя

Если нейрон не реагирует на шаблон ввода, то обучение в этом нейроне не происходит. Однако, если конкретный нейрон выигрывает, то соответствующие веса корректируются следующим образом:

$$\ Delta w_ {kj} \: = \: \ begin {case} - \ alpha (x_ {j} \: - \: w_ {kj}), &amp;amp; if \: нейрон \: k \: wins \\ 0 &amp;amp; if \: нейрон \: k \: убытки \ конец {случаи}$$

Здесь $\ alpha$ — скорость обучения.

Это ясно показывает, что мы отдаем предпочтение выигрышному нейрону, регулируя его вес, и, если нейрон потерян, нам не нужно беспокоиться о том, чтобы перенастроить его вес.

Алгоритм кластеризации K-средних

K-means — один из самых популярных алгоритмов кластеризации, в котором мы используем концепцию процедуры разбиения. Мы начинаем с исходного раздела и многократно перемещаем шаблоны из одного кластера в другой, пока не получим удовлетворительный результат.

Алгоритм

Шаг 1 — Выберите k точек в качестве начальных центроидов. Инициализируйте k прототипов (w ₁ ,…, w _k ) , например, мы можем отождествить их со случайно выбранными входными векторами —

Wj=ip,гдеj in lbrace1,....,k rbraceиp в lbrace1,....,n rbrace $$W_ {j} \: = \: i_ {p}, \: \: \: где \: j \: \ in \ lbrace1, ...., k \ rbrace \: и \: p \: \ в \ lbrace1, ...., n \ rbrace$$

Каждый кластер C _j связан с прототипом w _j .

Шаг 2 — Повторяйте шаг 3-5, пока E больше не уменьшится или членство в кластере больше не изменится.

Шаг 3 — Для каждого входного вектора i _p, где p ∈ {1,…, n} , положить i _p в кластер C _{j *} с ближайшим прототипом w _{j *,} имеющим следующее соотношение

|ip−wj∗| leq|ip−wj|,j in lbrace1,....,к rbrace $$| i_ {p} \: - \: w_ {j *} | \: \ leq \: | i_ {p} \: - \: w_ {j} |, \: j \: \ in \ lbrace1, ...., к \ rbrace$$

Шаг 4 — Для каждого кластера C _j , где j ∈ {1,…, k} , обновите прототип w _j, чтобы он был центром тяжести всех выборок, в настоящее время находящихся в C _j , так, чтобы

wj= sumip inCj fracip|Cj| $$w_ {j} \: = \: \ sum_ {i_ {p} \ in C_ {j}} \ frac {i_ {p}} {| C_ {j} |}$$

Шаг 5 — Рассчитать общую ошибку квантования следующим образом —

E= sumkj=1 sumip inwj|ip−wj|2 $$E \: = \: \ sum_ {j = 1} ^ k \ sum_ {i_ {p} \ in w_ {j}} | i_ {p} \: - \: w_ {j} | ^ 2$$

Неокогнитрон

Это многослойная сеть прямой связи, которая была разработана Fukushima в 1980-х годах. Эта модель основана на контролируемом обучении и используется для визуального распознавания образов, в основном рукописных символов. Это в основном расширение сети Cognitron, которая также была разработана компанией Fukushima в 1975 году.

Архитектура

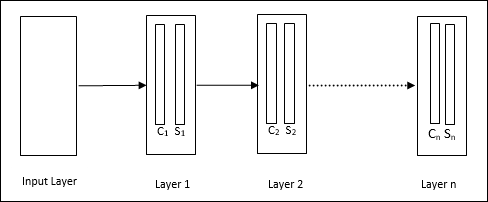
Это иерархическая сеть, которая включает в себя много уровней, и в этих слоях существует локальная схема подключения.

Как мы видели на приведенной выше диаграмме, неокогнитрон делится на разные связанные слои, и каждый слой имеет две клетки. Объяснение этих клеток заключается в следующем —

S-ячейка — она ​​называется простой ячейкой, которая обучается реагировать на определенный шаблон или группу шаблонов.

C-Cell — называется сложной ячейкой, которая объединяет выходные данные S-ячейки и одновременно уменьшает количество единиц в каждом массиве. В другом смысле C-клетка вытесняет результат S-клетки.

Алгоритм обучения

Тренировка неокогнитрона, как находят, прогрессирует слой за слоем. Веса от входного слоя до первого слоя обучаются и замораживаются. Затем тренируются веса от первого до второго слоя и так далее. Внутренние вычисления между S-ячейкой и Ccell зависят от весов, поступающих с предыдущих слоев. Следовательно, можно сказать, что алгоритм обучения зависит от расчетов на S-элементе и C-элементе.

Расчеты в S-ячейке

S-клетка обладает возбуждающим сигналом, полученным от предыдущего уровня, и обладает ингибирующими сигналами, полученными в том же слое.

 theta= sqrt sum sumtic2i $$\ theta = \: \ sqrt {\ sum \ sum t_ {i} c_ {i} ^ 2}$$

Здесь t _i — фиксированный вес, а c _i — выходной сигнал C-ячейки.

Масштабированный вход S-ячейки может быть рассчитан следующим образом:

х= гидроразрыва1 +е1 +vw0−1 $$х \: = \: \ гидроразрыва {1 \ + \: е} {1 \ + \: vw_ {0}} \: - \: 1$$

Здесь e= sumiciwi$e \: = \: \ sum_i c_ {i} w_ {i}$

w _i — вес, скорректированный от C-клетки до S-клетки.

w ₀ — вес, регулируемый между входом и S-ячейкой.

v — возбуждающий вход от С-клетки.

Активация выходного сигнала:

$$s \: = \: \ begin {case} x, &amp;amp; if \: x \ geq 0 \\ 0, &amp;amp; if \: x &amp;lt;0 \ end {case}$$

Расчеты в C-ячейке

Чистый вход C-слоя

C= displaystyle sum limitisixi $$C \: = \: \ displaystyle \ sum \ limit_i s_ {i} x_ {i}$$

Здесь s _i — выходной сигнал от S-ячейки, а x _i — фиксированный вес от S-ячейки до C-ячейки.

Окончательный результат выглядит следующим образом —

$$C_ {out} \: = \: \ begin {case} \ frac {C} {a + C}, &amp;amp; if \: C&amp;gt; 0 \\ 0, а в противном случае \ end {case}$$

Здесь «а» — это параметр, который зависит от производительности сети.