Контролируемое обучение

Как следует из названия, контролируемое обучение происходит под наблюдением учителя. Этот процесс обучения является зависимым. Во время обучения ANN при контролируемом обучении входной вектор представляется в сеть, которая создает выходной вектор. Этот выходной вектор сравнивается с желаемым / целевым выходным вектором. Сигнал ошибки генерируется, если существует разница между фактическим выходным сигналом и вектором требуемого / целевого выходного сигнала. На основе этого сигнала ошибки веса будут корректироваться до тех пор, пока фактический выходной сигнал не будет сопоставлен с желаемым выходным значением.

Perceptron

Разработанный Фрэнком Розенблаттом с использованием модели МакКаллоха и Питтса, персептрон является основной операционной единицей искусственных нейронных сетей. Он использует контролируемое правило обучения и может классифицировать данные на два класса.

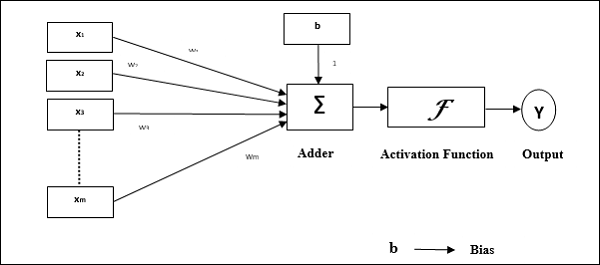
Эксплуатационные характеристики персептрона: он состоит из одного нейрона с произвольным числом входов и регулируемыми весами, но выход нейрона равен 1 или 0 в зависимости от порога. Он также состоит из смещения, вес которого всегда равен 1. Следующий рисунок дает схематическое представление персептрона.

Перцептрон, таким образом, имеет следующие три основных элемента —

• Ссылки — это будет набор ссылок для соединения, который имеет вес, включая смещение, всегда имеющее вес 1.

• Сумматор — добавляет данные после умножения их на соответствующие веса.

• Функция активации — ограничивает выход нейрона. Самая основная функция активации — это пошаговая функция Хевисайда, имеющая два возможных выхода. Эта функция возвращает 1, если вход положительный, и 0 для любого отрицательного входа.

Ссылки — это будет набор ссылок для соединения, который имеет вес, включая смещение, всегда имеющее вес 1.

Сумматор — добавляет данные после умножения их на соответствующие веса.

Функция активации — ограничивает выход нейрона. Самая основная функция активации — это пошаговая функция Хевисайда, имеющая два возможных выхода. Эта функция возвращает 1, если вход положительный, и 0 для любого отрицательного входа.

Алгоритм обучения

Сеть Perceptron может быть обучена как для одного устройства вывода, так и для нескольких устройств вывода.

Алгоритм обучения для одного блока вывода

Шаг 1 — Инициализируйте следующее, чтобы начать тренировку —

• Веса
• предвзятость
• Скорость обучения $\ alpha$

Для простоты расчета и простоты веса и смещения должны быть установлены равными 0, а скорость обучения должна быть установлена ​​равной 1.

Шаг 2 — Продолжайте шаг 3-8, если условие остановки не соответствует действительности.

Шаг 3 — Продолжайте шаг 4-6 для каждого вектора тренировки x .

Шаг 4 — Активируйте каждый блок ввода следующим образом —

Xя=Sя :(я=1кп) $$X_ {я} \: = \: S_ {я} \ 🙁 я \: = \: 1 \: к \: п)$$

Шаг 5 — Теперь получите чистый вход со следующим соотношением —

yin=b+ displaystyle sum limitnixi.wi $$y_ {in} \: = \: b \: + \: \ displaystyle \ sum \ limit_ {i} ^ n x_ {i}. \: w_ {i}$$

Здесь «b» — это смещение, а «n» — общее количество входных нейронов.

Шаг 6 — Примените следующую функцию активации для получения окончательного результата.

$$f (y_ {in}) \: = \: \ begin {case} 1 & if \: y_ {in} \:> \: \ theta \\ 0 & if \: - \ theta \: \ leqslant \ : y_ {in} \: \ leqslant \: \ theta \\ - 1 & if \: y_ {in} \: <\: - \ theta \ end {case}$$

Шаг 7 — Отрегулируйте вес и уклон следующим образом —

Случай 1 — если у, то

wя(новый)=wя(старый) + альфаtxя $$w_ {я} (новый) \: = \: w_ {я} (старый) \ + \: \ альфа \: tx_ {я}$$

b(новый)=b(старый)+ alphat $$b (новый) \: = \: b (старый) \: + \: \ alpha t$$

Случай 2 — если у = т, то

wя(новый)=wя(старый) $$w_ {я} (новый) \: = \: w_ {я} (старый)$$

б(новый)=Ь(старый) $$б (новый) \: = \: Ь (старый)$$

Здесь «y» — фактический выход, а «t» — желаемый / целевой выход.

Шаг 8 — Проверьте состояние остановки, которое может произойти, если нет изменения веса.

Алгоритм обучения для нескольких выходных единиц

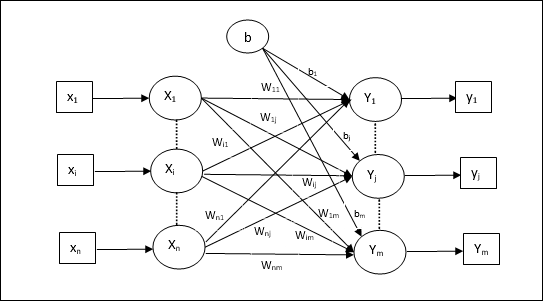
Следующая диаграмма — архитектура персептрона для нескольких выходных классов.

Шаг 1 — Инициализируйте следующее, чтобы начать тренировку —

• Веса
• предвзятость
• Скорость обучения $\ alpha$

Для простоты расчета и простоты веса и смещения должны быть установлены равными 0, а скорость обучения должна быть установлена ​​равной 1.

Шаг 2 — Продолжайте шаг 3-8, если условие остановки не соответствует действительности.

Шаг 3 — Продолжайте шаг 4-6 для каждого вектора тренировки x .

Шаг 4 — Активируйте каждый блок ввода следующим образом —

Xя=Sя :(я=1кп) $$X_ {я} \: = \: S_ {я} \ 🙁 я \: = \: 1 \: к \: п)$$

Шаг 5 — Получить чистый вход со следующим соотношением —

yin=b+ displaystyle sum limitnixiwij $$y_ {in} \: = \: b \: + \: \ displaystyle \ sum \ limit_ {i} ^ n x_ {i} \: w_ {ij}$$

Здесь «b» — это смещение, а «n» — общее количество входных нейронов.

Шаг 6 — Примените следующую функцию активации, чтобы получить окончательный результат для каждого блока вывода от j = 1 до m —

$$f (y_ {in}) \: = \: \ begin {case} 1 & if \: y_ {inj} \:> \: \ theta \\ 0 & if \: - \ theta \: \ leqslant \ : y_ {inj} \: \ leqslant \: \ theta \\ - 1 & if \: y_ {inj} \: <\: - \ theta \ end {case}$$

Шаг 7 — Отрегулируйте вес и смещение для x = 1 до n и j = 1 до m следующим образом —

Случай 1 — если y _j ≠ t _j, то

wIJ(новый)=wIJ(старый) + альфаtjXя $$w_ {IJ} (новый) \: = \: w_ {IJ} (старый) \ + \: \ альфа \: t_ {j} X_ {я}$$

bj(новый)=bj(старый)+ alphatj $$b_ {j} (новый) \: = \: b_ {j} (старый) \: + \: \ alpha t_ {j}$$

Случай 2 — если y _j = t _j, то

wIJ(новый)=wIJ(старый) $$w_ {IJ} (новый) \: = \: w_ {IJ} (старый)$$

bJ(новый)=bJ(старый) $$b_ {J} (новый) \: = \: b_ {J} (старый)$$

Здесь «y» — фактический выход, а «t» — желаемый / целевой выход.

Шаг 8 — Проверьте состояние остановки, которое произойдет, если нет изменения веса.

Адаптивный линейный нейрон (адалин)

Adaline, что означает адаптивный линейный нейрон, представляет собой сеть, имеющую одну линейную единицу. Он был разработан Видроу и Хоффом в 1960 году. Некоторые важные моменты об Адалине заключаются в следующем:

• Используется функция биполярной активации.

• Он использует дельта-правило для обучения, чтобы минимизировать среднеквадратичную ошибку (MSE) между фактическим выходом и желаемым / целевым выходом.

• Веса и уклон регулируются.

Используется функция биполярной активации.

Он использует дельта-правило для обучения, чтобы минимизировать среднеквадратичную ошибку (MSE) между фактическим выходом и желаемым / целевым выходом.

Веса и уклон регулируются.

Архитектура

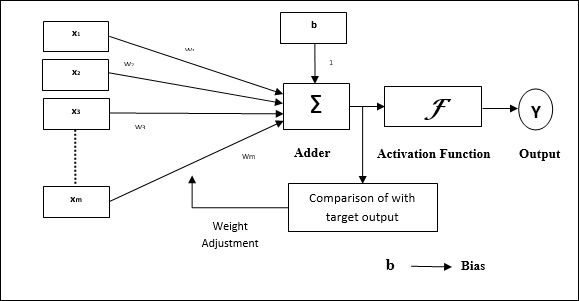
Базовая структура Adaline аналогична персептрону, имеющему дополнительную петлю обратной связи, с помощью которой фактический выход сравнивается с желаемым / целевым выходом. После сравнения на основе алгоритма обучения веса и смещения будут обновлены.

Алгоритм обучения

Шаг 1 — Инициализируйте следующее, чтобы начать тренировку —

• Веса
• предвзятость
• Скорость обучения $\ alpha$

Для простоты расчета и простоты веса и смещения должны быть установлены равными 0, а скорость обучения должна быть установлена ​​равной 1.

Шаг 2 — Продолжайте шаг 3-8, если условие остановки не соответствует действительности.

Шаг 3 — Продолжайте шаг 4-6 для каждой биполярной тренировочной пары s: t .

Шаг 4 — Активируйте каждый блок ввода следующим образом —

Xя=Sя :(я=1кп) $$X_ {я} \: = \: S_ {я} \ 🙁 я \: = \: 1 \: к \: п)$$

Шаг 5 — Получить чистый вход со следующим соотношением —

yin=b+ displaystyle sum limitnixiwi $$y_ {in} \: = \: b \: + \: \ displaystyle \ sum \ limit_ {i} ^ n x_ {i} \: w_ {i}$$

Здесь «b» — это смещение, а «n» — общее количество входных нейронов.

Шаг 6 — Примените следующую функцию активации для получения окончательного результата —

$$f (y_ {in}) \: = \: \ begin {case} 1 & if \: y_ {in} \: \ geqslant \: 0 \\ - 1 & if \: y_ {in} \: < \: 0 \ end {case}$$

Шаг 7 — Отрегулируйте вес и уклон следующим образом —

Случай 1 — если у, то

wi(новый)=wi(старый)+ alpha(t−yin)xi $$w_ {i} (новый) \: = \: w_ {i} (старый) \: + \: \ alpha (t \: - \: y_ {in}) x_ {i}$$

b(новый)=b(старый)+ alpha(t−yin) $$b (новый) \: = \: b (старый) \: + \: \ alpha (t \: - \: y_ {in})$$

Случай 2 — если у = т, то

wя(новый)=wя(старый) $$w_ {я} (новый) \: = \: w_ {я} (старый)$$

б(новый)=Ь(старый) $$б (новый) \: = \: Ь (старый)$$

Здесь «y» — фактический выход, а «t» — желаемый / целевой выход.

(t−yin)$(t \: - \; y_ {in})$ — это вычисленная ошибка.

Шаг 8 — Проверка состояния остановки, которое произойдет, когда нет изменений в весе или когда наибольшее изменение веса произошло во время тренировки, меньше указанного допуска.

Множественный адаптивный линейный нейрон (Madaline)

Madaline, что означает Multiple Adaptive Linear Neuron, представляет собой сеть, которая состоит из множества Adalines параллельно. У него будет один выходной блок. Вот некоторые важные моменты, касающиеся Мадалины:

• Это похоже на многослойный персептрон, где Adaline будет действовать как скрытая единица между входом и слоем Madaline.

• Веса и смещение между входным и адалиновым слоями, как мы видим в архитектуре Adaline, являются регулируемыми.

• Слои Adaline и Madaline имеют фиксированные веса и смещения 1.

• Обучение можно проводить с помощью правила Delta.

Это похоже на многослойный персептрон, где Adaline будет действовать как скрытая единица между входом и слоем Madaline.

Веса и смещение между входным и адалиновым слоями, как мы видим в архитектуре Adaline, являются регулируемыми.

Слои Adaline и Madaline имеют фиксированные веса и смещения 1.

Обучение можно проводить с помощью правила Delta.

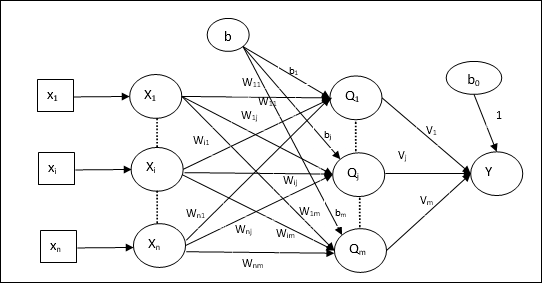
Архитектура

Архитектура Madaline состоит из «n» нейронов входного слоя, «m» нейронов уровня Adaline и 1 нейрона слоя Madaline. Слой Adaline можно рассматривать как скрытый слой, поскольку он находится между входным слоем и выходным слоем, то есть слоем Madaline.

Алгоритм обучения

К настоящему времени мы знаем, что должны регулироваться только веса и смещения между входным слоем и слоем Adaline, а веса и смещения между слоем Adaline и Madaline являются фиксированными.

Шаг 1 — Инициализируйте следующее, чтобы начать тренировку —

• Веса
• предвзятость
• Скорость обучения $\ alpha$

Для простоты расчета и простоты веса и смещения должны быть установлены равными 0, а скорость обучения должна быть установлена ​​равной 1.

Шаг 2 — Продолжайте шаг 3-8, если условие остановки не соответствует действительности.

Шаг 3 — Продолжайте шаг 4-6 для каждой биполярной тренировочной пары s: t .

Шаг 4 — Активируйте каждый блок ввода следующим образом —

Xя=Sя :(я=1кп) $$X_ {я} \: = \: S_ {я} \ 🙁 я \: = \: 1 \: к \: п)$$

Шаг 5 — Получить чистую входную информацию на каждом скрытом слое, т.е. слое Adaline со следующим соотношением —

Qinj=bj+ displaystyle sum limitnixiwijj=1км $$Q_ {inj} \: = \: b_ {j} \: + \: \ displaystyle \ sum \ limit_ {i} ^ n x_ {i} \: w_ {ij} \: \: \: j \: = \: 1 \: к \: м$$

Здесь «b» — это смещение, а «n» — общее количество входных нейронов.

Шаг 6 — Примените следующую функцию активации, чтобы получить окончательный результат на уровне Adaline и Madaline —

$$ f (x) \: = \: \ begin {case} 1 & if \: x \: \ geqslant \: 0 \\ — 1 & if \: x \: <\: 0 \ end {case} $ $

Выход на скрытый (Adaline) блок

QJ=F(Qинъек) $$Q_ {J} \: = \: F (Q_ {} инъек)$$

Конечный вывод сети

у=F(у−в) $$у \: = \: F (у- {в})$$

то есть yinj=b0+ summj=1Qjvj$\: \: y_ {inj} \: = \: b_ {0} \: + \: \ sum_ {j = 1} ^ m \: Q_ {j} \: v_ {j}$

Шаг 7 — Рассчитайте ошибку и откорректируйте веса следующим образом —

Случай 1 — если y ≠ t и t = 1, то

wij(новый)=wij(старый)+ alpha(1−Qinj)xi $$w_ {ij} (новый) \: = \: w_ {ij} (старый) \: + \: \ alpha (1 \: - \: Q_ {inj}) x_ {i}$$

bj(новый)=bj(старый)+ alpha(1−Qinj) $$b_ {j} (новый) \: = \: b_ {j} (старый) \: + \: \ alpha (1 \: - \: Q_ {inj})$$

В этом случае весовые коэффициенты будут обновлены в Q _j, где чистый входной сигнал близок к 0, поскольку t = 1 .

Случай 2 — если y ≠ t и t = -1, то

wik(новый)=wik(старый)+ alpha(−1−Qink)xi $$w_ {ik} (новый) \: = \: w_ {ik} (старый) \: + \: \ alpha (-1 \: - \: Q_ {ink}) x_ {i}$$

bk(новый)=bk(старый)+ alpha(−1−Qink)) $$b_ {k} (новый) \: = \: b_ {k} (старый) \: + \: \ alpha (-1 \: - \: Q_ {ink}))$$

В этом случае веса будут обновлены на Q _k, где чистый входной сигнал положительный, потому что t = -1 .

Здесь «y» — фактический выход, а «t» — желаемый / целевой выход.

Случай 3 — если у = т, то

Там не будет никаких изменений в весах.

Шаг 8 — Проверка состояния остановки, которое произойдет, когда нет изменений в весе или когда наибольшее изменение веса произошло во время тренировки, меньше указанного допуска.

Нейронные сети обратного распространения

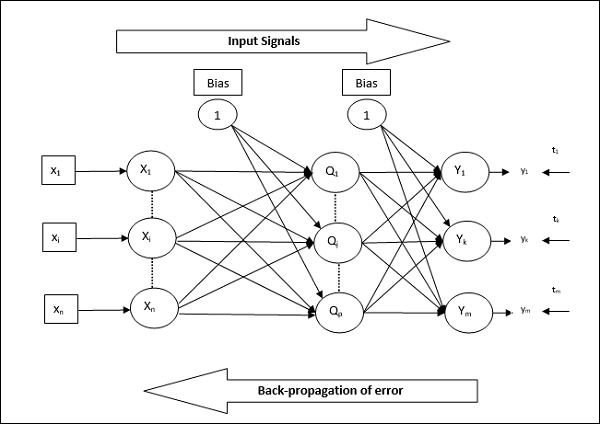
Back Propagation Neural (BPN) — это многослойная нейронная сеть, состоящая из входного слоя, как минимум одного скрытого слоя и выходного слоя. Как следует из названия, в этой сети будет происходить обратное распространение. Ошибка, которая вычисляется на выходном слое путем сравнения целевого и фактического выходных данных, будет распространяться обратно к входному слою.

Архитектура

Как показано на диаграмме, архитектура BPN имеет три взаимосвязанных уровня с весами на них. Скрытый слой и выходной слой также имеют смещение, вес которого всегда равен 1, на них. Как видно из диаграммы, работа BPN проходит в два этапа. Одна фаза отправляет сигнал с входного уровня на выходной уровень, а другая фаза обратно распространяет ошибку с выходного уровня на входной уровень.

Алгоритм обучения

Для обучения BPN будет использовать бинарную функцию активации сигмоида. Обучение BPN будет состоять из следующих трех этапов.

• Фаза 1 — Фаза прямой подачи

• Этап 2 — обратное распространение ошибки

• Этап 3 — Обновление весов

Фаза 1 — Фаза прямой подачи

Этап 2 — обратное распространение ошибки

Этап 3 — Обновление весов

Все эти шаги будут заключены в алгоритме следующим образом

Шаг 1 — Инициализируйте следующее, чтобы начать тренировку —

• Веса
• Скорость обучения $\ alpha$

Для простоты расчета и простоты возьмите несколько небольших случайных значений.

Шаг 2 — Продолжайте шаг 3-11, когда условие остановки не соответствует действительности.

Шаг 3 — Продолжайте шаги 4-10 для каждой тренировочной пары.

Фаза 1

Шаг 4 — Каждый входной блок получает входной сигнал x _i и отправляет его на скрытый блок для всех i = 1 до n

Шаг 5 — Рассчитать чистый вход в скрытой единице, используя следующее соотношение —

Qinj=b0j+ sumni=1xivijj= :1кр $$Q_ {inj} \: = \: b_ {0j} \: + \: \ sum_ {i = 1} ^ n x_ {i} v_ {ij} \: \: \: \: j \: = \ : 1 \: к \: р$$

Здесь b _0j — это смещение на скрытой единице, v _ij — вес на j единице скрытого слоя, поступающего из i единицы входного слоя.

Теперь вычислите чистый результат, применив следующую функцию активации

QJ=F(Qинъек) $$Q_ {J} \: = \: F (Q_ {} инъек)$$

Отправьте эти выходные сигналы скрытых единиц слоя на единицы выходного слоя.

Шаг 6 — Рассчитать чистый входной сигнал на единицу выходного слоя, используя следующее соотношение —

yink=b0k+ sumpj=1Qjwjkk= :1км $$y_ {ink} \: = \: b_ {0k} \: + \: \ sum_ {j = 1} ^ p \: Q_ {j} \: w_ {jk} \: \: k \: = \ : 1 \: к \: м$$

Здесь b 0k ⁡ — смещение на выходной единице, w _jk — вес на k единицу выходного слоя, приходящего из j единицы скрытого слоя.

Рассчитать чистый выход, применяя следующую функцию активации

у−к=F(у−чернил) $$у- {к} \: = \: F (у- {чернил})$$

Фаза 2

Шаг 7 — Вычислить член, исправляющий ошибки, в соответствии с целевым шаблоном, полученным на каждом выходном блоке, следующим образом:

 Deltaк= :(tк−yк)е(у−чернила) $$\ Delta_ {к} \: = \ 🙁 t_ {к} \: - \: y_ {к}) ^ {е} (у- {чернила})$$

Исходя из этого, обновите вес и уклон следующим образом —

 Deltavjk= alpha deltakQij $$\ Delta v_ {jk} \: = \: \ alpha \ delta_ {k} \: Q_ {ij}$$

 Deltab0k= alpha deltak $$\ Delta b_ {0k} \: = \: \ alpha \ delta_ {k}$$

Затем отправьте $\ delta_ {k}$ обратно в скрытый слой.

Шаг 8 — Теперь каждая скрытая единица будет суммой своих дельта-входов от выходных единиц.

 deltainj= displaystyle sum limitmk=1 deltakwjk $$\ delta_ {inj} \: = \: \ displaystyle \ sum \ limit_ {k = 1} ^ m \ delta_ {k} \: w_ {jk}$$

Срок ошибки можно рассчитать следующим образом —

 Deltaj= Deltaинъекце′(Qинъек) $$\ Delta_ {j} \: = \: \ Delta_ {} инъекц е ^ { '} (Q_ {} инъек)$$

Исходя из этого, обновите вес и уклон следующим образом —

 Deltawij= alpha deltajxi $$\ Delta w_ {ij} \: = \: \ alpha \ delta_ {j} x_ {i}$$

 Deltab0j= alpha deltaj $$\ Delta b_ {0j} \: = \: \ alpha \ delta_ {j}$$

Фаза 3

Шаг 9 — Каждый выходной блок (y _k k = 1 до m) обновляет вес и смещение следующим образом —

vjk(новый)=vjk(старый)+ Deltavjk $$v_ {jk} (новый) \: = \: v_ {jk} (старый) \: + \: \ Delta v_ {jk}$$

b0k(новый)=b0k(старый)+ Deltab0k $$b_ {0k} (новый) \: = \: b_ {0k} (старый) \: + \: \ Delta b_ {0k}$$

Шаг 10 — Каждый выходной блок (z _j j = 1 до p) обновляет вес и смещение следующим образом —

wij(новый)=wij(старый)+ Deltawij $$w_ {ij} (новый) \: = \: w_ {ij} (старый) \: + \: \ Delta w_ {ij}$$

b0j(новый)=b0j(старый)+ Deltab0j $$b_ {0j} (новый) \: = \: b_ {0j} (старый) \: + \: \ Delta b_ {0j}$$

Шаг 11 — Проверьте условие остановки, которое может быть либо количеством достигнутых эпох, либо целевым выходом, совпадающим с фактическим выходом.

Обобщенное правило обучения Delta

Дельта-правило работает только для выходного слоя. С другой стороны, обобщенное дельта-правило, также называемое правилом обратного распространения , является способом создания желаемых значений скрытого слоя.

Математическая формулировка

Для функции активации yk=f(yink)$y_ {k} \: = \: f (y_ {ink})$ вывод чистых входных данных на скрытом слое, а также на выходном слое может быть задан как

у−чернил= displaystyle сумма limitsiZяwJK $$у- {чернил} \: = \: \ displaystyle \ сумма \ limits_i \: Z_ {я} w_ {JK}$$

И yinj= sumixivij$\: \: y_ {inj} \: = \: \ sum_i x_ {i} v_ {ij}$

Теперь ошибка, которую нужно минимизировать,

Е= гидроразрыва12 displaystyle сумма limitsк[Tк−у−к]2 $$Е \: = \: \ гидроразрыва {1} {2} \ displaystyle \ сумма \ limits_ {к} \: [T_ {к} \: - \: у- {к}] ^ 2$$

Используя правило цепочки, мы имеем

 frac частичныйE частичныйwjk= frac частный частичныйwjk( frac12 displaystyle sum limitsк[tк−yк]2) $$\ frac {\ частичный E} {\ частичный w_ {jk}} \: = \: \ frac {\ частный} {\ частичный w_ {jk}} (\ frac {1} {2} \ displaystyle \ sum \ limits_ {к} \: [t_ {к} \: - \: y_ {к}] ^ 2)$$

= frac частный частичныйwjk lgroup frac12[tk−t(yink)]]2 rgroup $$= \: \ frac {\ частный} {\ частичный w_ {jk}} \ lgroup \ frac {1} {2} [t_ {k} \: - \: t (y_ {ink})]] ^ 2 \ rgroup$$

=−[tk−yk] frac частный частичныйwjkf(yчернила) $$= \: - [t_ {k} \: - \: y_ {k}] \ frac {\ частный} {\ частичный w_ {jk}} f (y_ {чернила})$$

=−[tk−yk]f(yчернила) frac частный частичныйwjk(yчернила) $$= \: - [t_ {k} \: - \: y_ {k}] f (y_ {чернила}) \ frac {\ частный} {\ частичный w_ {jk}} (y_ {чернила})$$

$$= \: - [T_ {к} \: - \: у- {к}] {е ^ '} ({у- чернил}) Z_ {J}$$

Теперь давайте скажем  deltak=−[tk−yk]f′(yink)$\ delta_ {k} \: = \: - [t_ {k} \: - \: y_ {k}] f ^ {'} (y_ {ink})$

Веса на соединениях со скрытой единицей z _j могут быть определены как —

 frac частичныйE частичныйvij=− displaystyle sum limitk deltak frac частный частичныйvij :(yчернила) $$\ frac {\ частичный E} {\ частичный v_ {ij}} \: = \: - \ displaystyle \ sum \ limit_ {k} \ delta_ {k} \ frac {\ частный} {\ частичный v_ {ij} } \ 🙁 y_ {чернила})$$

Положив значение $y_ {ink}$, получим следующее

 Deltaj=− displaystyle сумма limitsк DeltaкwЮ.К.е′(zинъек) $$\ Delta_ {j} \: = \: - \ displaystyle \ сумма \ limits_ {к} \ Delta_ {к} {w_ Ю.К.} е ^ { '} (z_ {} инъек)$$

Обновление веса может быть сделано следующим образом —

Для блока вывода —

 Deltawjk=− alpha frac частичныйE частичныйwjk $$\ Delta w_ {jk} \: = \: - \ alpha \ frac {\ частичный E} {\ частичный w_ {jk}}$$

= альфа DeltaкZJ $$= \: \ альфа \: \ Delta_ {к} \: Z_ {J}$$

Для скрытого юнита —

 Deltavij=− alpha frac частичныйE частичныйvij $$\ Delta v_ {ij} \: = \: - \ alpha \ frac {\ частичный E} {\ частичный v_ {ij}}$$

= альфа DeltaJXя $$= \: \ альфа \: \ Delta_ {J} \: X_ {я}$$