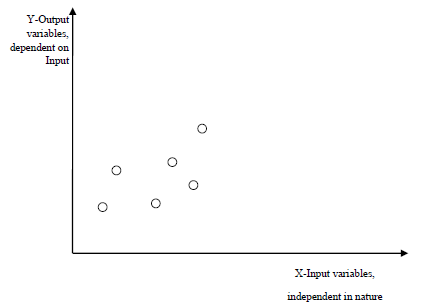
Регрессия является еще одним важным и широко используемым инструментом статистического и машинного обучения. Основная цель задач на основе регрессии — предсказать выходные метки или ответы, которые являются продолженными числовыми значениями, для заданных входных данных. Результат будет основан на том, что модель выучила на этапе обучения. В основном, регрессионные модели используют функции входных данных (независимые переменные) и соответствующие им непрерывные числовые выходные значения (зависимые или выходные переменные), чтобы узнать конкретную связь между входными данными и соответствующими выходными данными.
Типы регрессионных моделей
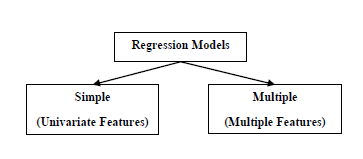
Модели регрессии бывают двух типов:
Простая регрессионная модель — это самая базовая регрессионная модель, в которой прогнозы формируются из единой, одномерной особенности данных.
Модель множественной регрессии. Как следует из названия, в этой модели регрессии прогнозы формируются из множества характеристик данных.
Построение регрессора в Python
Модель регрессора в Python может быть построена так же, как мы построили классификатор. Scikit-learn, библиотека Python для машинного обучения также может быть использована для создания регрессора в Python.
В следующем примере мы будем строить базовую регрессионную модель, которая будет соответствовать линии данных, то есть линейному регрессору. Необходимые шаги для построения регрессора в Python следующие:
Шаг 1: Импорт необходимого пакета Python
Для построения регрессора с помощью scikit-learn нам нужно импортировать его вместе с другими необходимыми пакетами. Мы можем импортировать, используя следующий скрипт —
import numpy as np from sklearn import linear_model import sklearn.metrics as sm import matplotlib.pyplot as plt
Шаг 2: Импорт набора данных
После импорта необходимого пакета нам понадобится набор данных для построения модели прогнозирования регрессии. Мы можем импортировать его из набора данных sklearn или использовать другой согласно нашему требованию. Мы собираемся использовать наши сохраненные входные данные. Мы можем импортировать его с помощью следующего скрипта —
input = r'C:\linear.txt'
Далее нам нужно загрузить эти данные. Мы используем функцию np.loadtxt для загрузки.
input_data = np.loadtxt(input, delimiter=',') X, y = input_data[:, :-1], input_data[:, -1]
Шаг 3: Организация данных в наборы для обучения и тестирования
Следовательно, поскольку нам необходимо протестировать нашу модель на невидимых данных, мы разделим наш набор данных на две части: обучающий набор и тестовый набор. Следующая команда выполнит это —
training_samples = int(0.6 * len(X)) testing_samples = len(X) - num_training X_train, y_train = X[:training_samples], y[:training_samples] X_test, y_test = X[training_samples:], y[training_samples:]
Шаг 4: Оценка модели и прогноз
После разделения данных на обучение и тестирование нам нужно построить модель. Для этой цели мы будем использовать функцию LineaRegression () Scikit-learn. Следующая команда создаст объект линейного регрессора.
reg_linear = linear_model.LinearRegression()
Затем, обучите эту модель с обучающими образцами следующим образом —
reg_linear.fit(X_train, y_train)
Теперь, наконец, нам нужно сделать прогноз с данными тестирования.
y_test_pred = reg_linear.predict(X_test)
Шаг 5: Сюжет и визуализация
После прогноза мы можем построить и визуализировать его с помощью следующего скрипта —
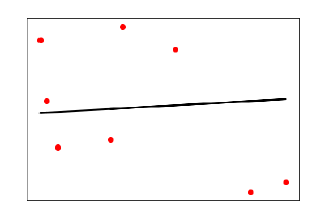
plt.scatter(X_test, y_test, color = 'red') plt.plot(X_test, y_test_pred, color = 'black', linewidth = 2) plt.xticks(()) plt.yticks(()) plt.show()
Выход
В приведенном выше выводе мы видим линию регрессии между точками данных.
Шаг 6: Расчет производительности. Мы также можем вычислить производительность нашей регрессионной модели с помощью различных метрик производительности следующим образом.
print("Regressor model performance:") print("Mean absolute error(MAE) =", round(sm.mean_absolute_error(y_test, y_test_pred), 2)) print("Mean squared error(MSE) =", round(sm.mean_squared_error(y_test, y_test_pred), 2)) print("Median absolute error =", round(sm.median_absolute_error(y_test, y_test_pred), 2)) print("Explain variance score =", round(sm.explained_variance_score(y_test, y_test_pred), 2)) print("R2 score =", round(sm.r2_score(y_test, y_test_pred), 2))
Выход
Regressor model performance: Mean absolute error(MAE) = 1.78 Mean squared error(MSE) = 3.89 Median absolute error = 2.01 Explain variance score = -0.09 R2 score = -0.09
Типы алгоритмов регрессии ML
Наиболее полезным и популярным алгоритмом регрессии ML является алгоритм линейной регрессии, который далее делится на два типа, а именно:
- Алгоритм простой линейной регрессии
- Алгоритм множественной линейной регрессии.
Мы обсудим это и реализуем на Python в следующей главе.
Приложения
Применения алгоритмов регрессии ML следующие:
Прогнозирование или прогнозный анализ. Одним из важных применений регрессии является прогнозирование или прогнозный анализ. Например, мы можем прогнозировать ВВП, цены на нефть или, проще говоря, количественные данные, которые меняются с течением времени.
Оптимизация — мы можем оптимизировать бизнес-процессы с помощью регрессии. Например, менеджер магазина может создать статистическую модель, чтобы понять время прихода покупателей.
Исправление ошибок — В бизнесе принятие правильного решения не менее важно, чем оптимизация бизнес-процесса. Регрессия может помочь нам принять правильное решение, а также исправить уже выполненное решение.
Экономика — это наиболее используемый инструмент в экономике. Мы можем использовать регрессию для прогнозирования спроса, предложения, потребления, инвестиций в запасы и т. Д.
Финансы — финансовая компания всегда заинтересована в минимизации портфеля рисков и хочет знать факторы, влияющие на клиентов. Все это можно предсказать с помощью регрессионной модели.