Учебники

ML — Алгоритм среднего сдвига кластеризации

Ноябрь 20, 2018

Как обсуждалось ранее, это еще один мощный алгоритм кластеризации, используемый в обучении без учителя. В отличие от кластеризации K-средних, она не делает никаких предположений; следовательно, это непараметрический алгоритм.

Алгоритм среднего сдвига в основном назначает точки данных кластерам итеративно, смещая точки в направлении наивысшей плотности точек данных, то есть центроида кластера.

Разница между алгоритмом K-Means и Mean-Shift заключается в том, что позже не нужно заранее указывать количество кластеров, поскольку количество кластеров будет определяться алгоритмом по данным.

Работа алгоритма среднего сдвига

Мы можем понять работу алгоритма кластеризации Mean-Shift с помощью следующих шагов:

  • Шаг 1 — Сначала начните с точек данных, назначенных их кластеру.

  • Шаг 2 — Далее этот алгоритм будет вычислять центроиды.

  • Шаг 3 — На этом шаге местоположение новых центроидов будет обновлено.

  • Шаг 4 — Теперь процесс будет повторен и перемещен в область более высокой плотности.

  • Шаг 5 — Наконец, он будет остановлен, как только центроиды достигнут позиции, из которой он не сможет двигаться дальше.

Шаг 1 — Сначала начните с точек данных, назначенных их кластеру.

Шаг 2 — Далее этот алгоритм будет вычислять центроиды.

Шаг 3 — На этом шаге местоположение новых центроидов будет обновлено.

Шаг 4 — Теперь процесс будет повторен и перемещен в область более высокой плотности.

Шаг 5 — Наконец, он будет остановлен, как только центроиды достигнут позиции, из которой он не сможет двигаться дальше.

Реализация в Python

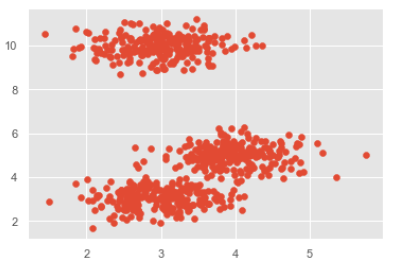
Это простой пример, чтобы понять, как работает алгоритм Mean-Shift. В этом примере мы сначала сгенерируем 2D-набор данных, содержащий 4 разных больших объекта, а затем применим алгоритм Mean-Shift, чтобы увидеть результат. 

%matplotlib inline
import numpy as np
from sklearn.cluster import MeanShift
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
from sklearn.datasets.samples_generator import make_blobs
centers = [[3,3,3],[4,5,5],[3,10,10]]
X, _ = make_blobs(n_samples = 700, centers = centers, cluster_std = 0.5)
plt.scatter(X[:,0],X[:,1])
plt.show()

Среднее смещение алгоритма

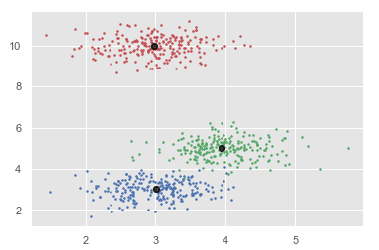
ms = MeanShift()
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
print(cluster_centers)
n_clusters_ = len(np.unique(labels))
print("Estimated clusters:", n_clusters_)
colors = 10*['r.','g.','b.','c.','k.','y.','m.']

for i in range(len(X)):
   plt.plot(X[i][0], X[i][1], colors[labels[i]], markersize = 3)
plt.scatter(cluster_centers[:,0],cluster_centers[:,1],
   marker = ".",color = 'k', s = 20, linewidths = 5, zorder = 10)
plt.show()

Выход 

[[ 2.98462798 9.9733794 10.02629344]
[ 3.94758484 4.99122771 4.99349433]
[ 3.00788996 3.03851268 2.99183033]]
Estimated clusters: 3

Создать набор данных

Преимущества и недостатки

преимущества

Ниже приведены некоторые преимущества алгоритма кластеризации Mean-Shift:

  • Не нужно делать какие-либо модельные допущения, как в случае K-средних или гауссовой смеси.

  • Он также может моделировать сложные кластеры, которые имеют невыпуклую форму.

  • Требуется только один параметр с именем bandwidth, который автоматически определяет количество кластеров.

  • Там нет вопроса локальных минимумов, как в K-средних.

  • Нет проблем, генерируемых выбросами.

Не нужно делать какие-либо модельные допущения, как в случае K-средних или гауссовой смеси.

Он также может моделировать сложные кластеры, которые имеют невыпуклую форму.

Требуется только один параметр с именем bandwidth, который автоматически определяет количество кластеров.

Там нет вопроса локальных минимумов, как в K-средних.

Нет проблем, генерируемых выбросами.

Недостатки

Ниже приведены некоторые недостатки алгоритма кластеризации Mean-Shift:

Алгоритм среднего сдвига не работает хорошо в случае большой размерности, где количество кластеров резко меняется.

У нас нет прямого контроля над количеством кластеров, но в некоторых приложениях нам нужно определенное количество кластеров.

Он не может различить осмысленные и бессмысленные способы.

154
Share: